不同施工方法在软弱围岩竖井中适应性研究

张 乾，吴 冬

(西南交通大学土木工程学院，四川成都 610031)

1 工程背景

随着我国西部交通事业的快速发展，越来越多的隧道通风竖井需在复杂地质条件下修建，针对竖井的施工方法有大量学者进行了研究，代鑫[1]等通过有限元模拟分析了竖井结构受力规律与模式；姚亚辉[2]等通过对竖井开挖过程数值模拟，得到了井壁变形规律，并提出在地层分界处应加强支护；吴迪[3]利用ANSYS对不同工况下竖井开挖进行模拟，分析了竖井围岩的稳定性；毕思文[4]等对煤矿竖井结构破坏因素进行探讨，得到其破坏机理；周荣[5]以大坪里隧道3#竖井施工实例，对施工过程中围岩位移及应力进行了分析；齐小勇[6]对秦岭终南山隧道通风竖井进行施工过程模拟，对支护结构的安全性与可行性进行了分析。

借鉴前人大量的有益成果，本文以某公路隧道的通风竖井为研究背景，竖井全长314.5 m，内径7 m，內空断面积36.64 m2，全段为Ⅴ级围岩，岩性主要为中微风化板岩，以薄层状结构为主，层间结合较差，岩体破碎，无支护时围岩易坍塌。拟通过数值模拟对该竖井在修建期间的施工方法进行分析，探讨不同施工方案下衬砌的受力变形，围岩位移及塑性区分布情况。

2 数值模型建立

2.1 计算模型建立

结合现场实际，充分考虑边界效应，计算模型长和宽均为100 m，高60 m；同时为保证计算精度并降低计算量，本次计算采用1/4对称模型，且对竖井开挖及相邻区域10 m×10 m范围内网格进行加密处理，疏密网格单元尺寸比例为1∶2，接触面采用Attach命令连接，网格剖分见图1所示。根据轴对称模型特点，模型对称面上施加法向位移约束，模型顶面及侧面施加应力约束，模型底部施加竖向位移约束，如图2所示。同时为简化计算，选取研究段埋深为-100～-160 m，本次计算模型划分单元6.48万个，节点71 105个，计算采用摩尔库伦模型。依据提供的地应力测试报告，竖井受区域构造应力影响严重，最大水平应力方向在N8 °W方向，模拟近似简化取X方向，详见图2。

图1 数值计算模型

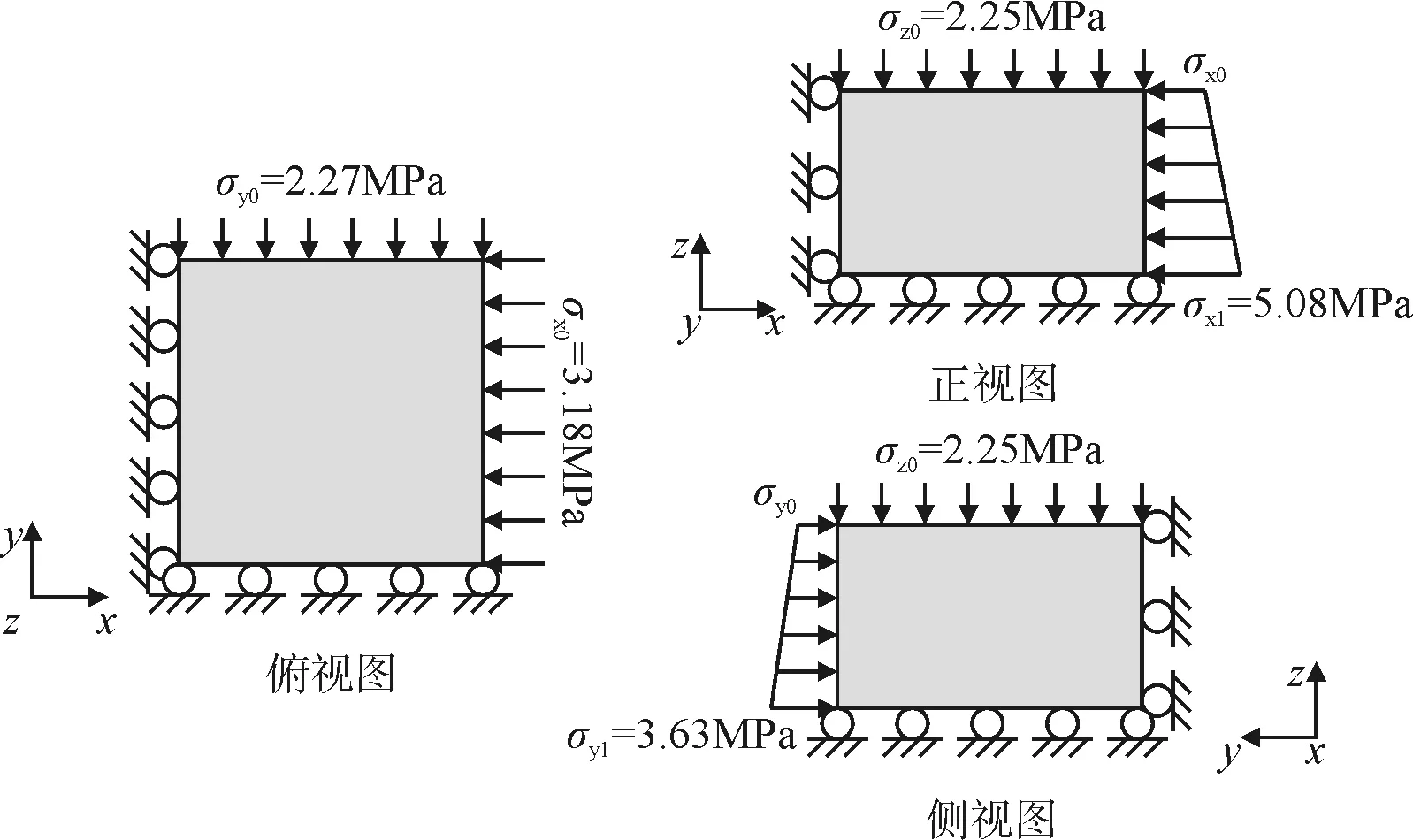
图2 计算边界条件

2.2 计算参数的确定

根据现场钻探获取岩样室内试验并结合JTG D70-2004《公路隧道设计规范》[7]确定的岩体力学参数见表1。

表1 岩体力学参数

模拟段支护参数为：初次支护采用喷射厚22 cmC25混凝土，Φ22药卷锚杆长2.5 m、0.6 m×1.2 m布置，Φ6.5 mm钢筋网，I16@0.8 m钢架，采用shell单元模拟；二次衬砌采用模筑厚50 cm C30混凝土(表2)。

表2 支护力学参数

对于Ⅴ级围岩支护为钢拱架喷锚联合支护，采用将钢拱架和钢筋网的弹性模量折算给混凝土，其计算方法为：

式中：Ec为折算后混凝土弹性模量；E0为原混凝土弹性模量；As为钢拱架截面积；Es为钢材弹模；Ac为混凝土面积。

2.3 模拟施工方案

为探讨不同施工方法在软弱地层中修建竖井的适应性问题，采用有限差分软件FLAC3D进行施工过程的动态模拟。模拟施工方案均采用正井法施工，根据初支与二衬的施作顺序，分为全井单行作业法、长段平行作业法、短段单行作业法，具体工序见表3所示。

表3 模拟施工方案表

3 计算结果分析

3.1 围岩位移分析

为避免模型端部影响，监测节点设置在模型中部(-30 m)围岩内，数值模拟中一次开挖进尺为4 m，初次支护与二次支护一次施作也为4 m，故监测点在开挖至-28 m前为支护前的位移释放，对应支护前围岩应力释放程度。在开挖至-32 m后，根据初支和二衬的施作顺序的不同，产生的位移量也不相同，如图3所示。

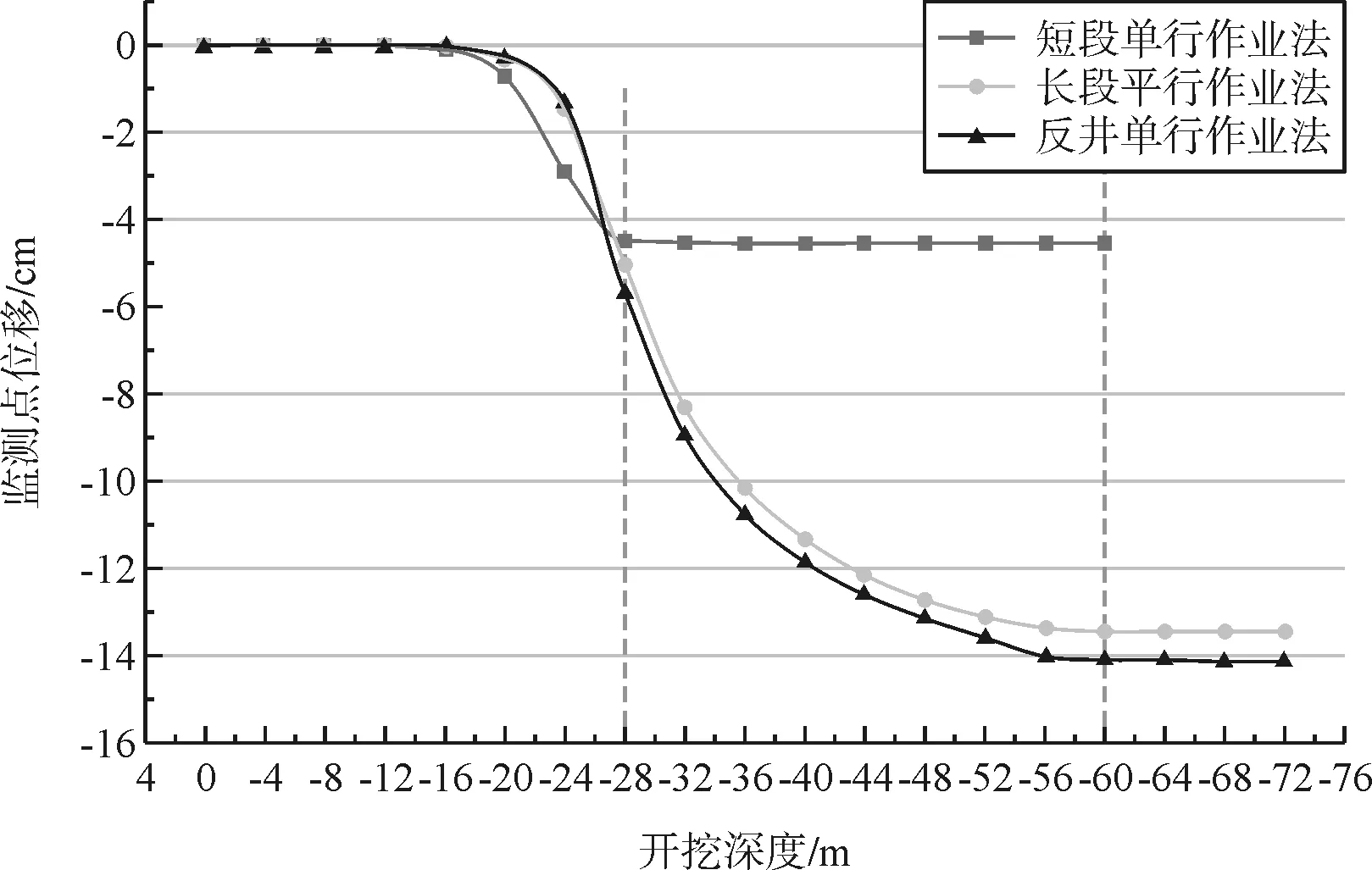
图3 -30m监测点随开挖深度位移

从图3 中可以看出，在短段单行作业中初支与二衬一起施作，紧跟工作面，围岩位移主要发生在施加支护前，为4.48 cm，占总体位移98 %，施加衬砌后仅发生0.09 cm位移，可见施加衬砌后围岩的位移得到有效控制。

在长段平行作业中初次支护紧跟工作面，因采用双吊盘作业，为保障施工便利性，要求施工间距大于30 m，故选取二次衬砌滞后初支32 m，此施工方法在竖井开挖后及时施作初次支护，保证围岩完整性，同时初次支护作为柔性支护，允许围岩发生一定位移，产生一定的应力释放后施作二次支护，施加初支前产生5.08 cm，占总体位移37.3 %，在施加初支后至施加二衬前发生8.38 cm，占比62 %，初支与二衬共同作用后产生0.014 cm位移。说明在支护的前期虽有一定的应力释放，但初支并未对围岩位移产生有效的约束，在施加二衬后才有效控制住围岩位移。

在全井单行作业中初支仍紧跟工作面一直施作到井底，后续反井进行二衬浇筑，监测点位移走势与长段平行作业相似，但大于其位移。在初支施加前发生5.7 cm，占总体位移40 %，施加后直到围岩位移稳定，产生8.42 cm，占比60 %，围岩应力释放与最终位移均大于长段平行作业法，二衬施作晚，围岩未能得到及时约束。

对比三种开挖方法，采用短段单行作业的围岩位移释放率最大，其产生的最终位移最小，长段平行与全井单行围岩位移释放率与最终位移都相接近，并发现监测点产生的位移释放主要集中在开挖的前两步，约占总释放位移的90 %。

3.2 支护结构受力分析

除去模型端部的影响，记录初次支护与二次衬砌在埋深(-114～-152 m)范围内的最大主应力，如图4 所示。从受力大小与变化规律上分析三种施工方法，发现采用短段单行作业法的初支受力最小，二衬受力最大，初支强度未得到充分利用，这是由于初支与二衬同步施作，初期围岩应力释放小，后期受力主要由二衬承担，为强支护方案；全井单行作业法的初支受力最大，二衬受力最小，前期采用初支来抵抗围岩变形，后期二衬受力很小，主要作为安全储备，但在现定的支护参数下，初支强度明显无法对围岩位移进行有效约束；而长段平行作业法的初支与二衬受力大小介于前两者施工方法之间，初支和二衬均发挥承载作用，但仍存在围岩位移释放过大的问题，证明初支强度与二衬间的施作间隔仍需进一步优化。从支护结构的受力上看，长段平行与全井单行法初支受力较大，并未有效约束围岩位移，短段单行作业虽二衬受力大，但在安全范围内，并对围岩进行及时约束。

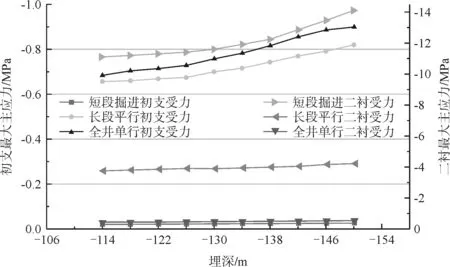
图4 不同方案下初支与二衬受力变化

3.3 塑性区分布状态

通过比较不同施工方法下开挖第十三步的塑性区状态(图5)，发现围岩塑性区主要以剪切型为主，整体成锥体分布，短段单行作业法形成的塑性区范围最小，长段平行作业与全井单行作业形成的塑性区范围最大且两者十分相近。由于初次支护与二次衬砌施加的时机不同，竖井围岩剪切塑性区的具体状态也不同，短段单行作业形成已经发生剪切破坏塑性区(Shear-p)由井口至二衬施加位置，正在发生剪切破坏的塑性区(Shear-n)在施加二衬位置至开挖面底部4.5 m左右；长段平行作业Shear-p状态塑性区由井口至二衬施加位置，Shear-n状态塑性区在施加二衬位置至开挖面底部8 m左右；全井单行作业Shear-n状态塑性区由井口至开挖面底部8 m左右；可以看出二衬施加后塑性区由Shear-n转化为Shear-p，短段单行形成的Shear-n段最小，长段平行次之，全井单行最大。对比塑性区的分布范围和具体状态，得出短段单行作业法对围岩控制要好于长段平行与全井单行作业法。

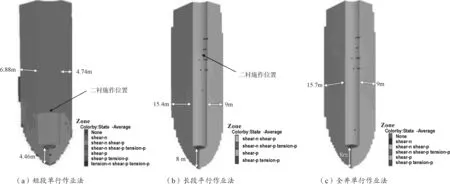
图5 各方案开挖第十三步塑性区状态

4 结论

通过从围岩位移、支护结构受力和围岩塑性区分布情况，对比分析三种施工方法在软弱地层中修建竖井的适应性，得到以下结论：

(1) 在软弱地层中，采用已定的支护参数下短段单行作业法产生的围岩位移要明显小于长段平行与全井单行作业法，且围岩产生的位移主要集中在开挖前后两个循环。

(2)在支护结构受力中，短段单行和全井单行作业中初支或二衬的强度未充分利用，长段平行作业中初支与二衬的受力相比其它工法更加合理，但其支护强度与施作时机仍需进一步讨论。

(3) 在开挖形成的椎体塑性区，短段单行形成的塑性区范围最小，长段平行与全井单行形成的塑性区范围相近，但正在发生剪切破坏的塑性区范围不同。

(4) 综合比选下，短段单行作业法相比其余两种工法在软弱地层中修建竖井具有明显优势，该计算分析可为现场后续施工或其它类似工程提供参考借鉴。