借教材，拓思维——数列教学的实践与思考

云南 段朝龙

在我们的实际教学中，教材上概念、公式、例题及习题的教学是我们整个数学教学活动的核心，教材也是学生思维拓展和能力培养的主要载体.因此，应充分理解和把握教材，充分挖掘教材所蕴藏的思维方法，同时认真研究课本相关知识的来龙去脉，对例题、习题进行深度剖析，对典型的问题，需要从多个角度挖掘其蕴含的思维价值，并结合学生的实际加以适当的构造和拓展，努力引导学生学以致用，这样才能更好地提升教育教学质量，才能更好地培养和发展学生的数学思维．

美国教育家苏娜丹戴克说过:“告诉我,我会忘记,做给我看,我会记住,让我参加,我就会完全理解.”因此在实际教学中，我们一线教师更重要的应该是培养学生独立思考和钻研的习惯和能力，激发学生的发散性思维和创造性思维.

著名的教育家叶圣陶曾说过：“教材只能作为授课的依据，要教得好，使学生受到实益，还得靠教师的善于应用.”“问题是数学的心脏.”学生的数学学科核心素养是在学生与情境、问题的有效互动中提升的.在实际教学过程中，我们不难发现很多知识可以在问题中直接使用，但也有很多知识、思想、方法隐藏在教材例题、习题的背后.而且历来高考命题都非常重视回归教材，回归课本，正所谓追本溯源，故而我们一线教师在实践过程中，更应该真正尊重教材，研究教材、拓展教材和活用教材，深度体会和掌握知识形成的思维过程.进一步探求例题、习题背后蕴藏着的教学价值，对相关内容进行总结、再造和升华，真正使例题、习题成为我们获取知识、拓展思维、提升能力的又一个重要载体．而且课本中很多例题、习题都非常具有典型性和可研性，是我们教育教学中真正的精华.我们应对这些问题进行充分的探究和拓展，激活教材，融会贯通，提高师生的钻研意识和研究能力，更好的发展学生思维和提升教学质量．

本文的核心即就数列教学中如何借用教材对学生进行思维拓展，如何挖掘教材例题、习题的应用价值和思维价值，谈一点自己的实践感受和思考．

一、借用教材的相关推导和演示.理解知识的生成过程，进而引领学生进行归纳和探究，激发学生的内部动机和兴趣，培养学生的研究欲望.

【例1】等差数列前n项和公式是什么？怎样推导的？高斯算法的妙处在哪里？再想一想还有其他推导方法吗？(人教A版,数学必修5第二章数列第42页探究)

证明：∵Sn=a1+a2+a3+…+an.① ∴Sn=an+an-1+an-2+…+a1.②

①+②得2Sn=(a1+an)+(a2+an-1)+(a3+an-2)+…+(an+a1).

让学生充分体会高斯算法的巧妙之处，进而采用倒序相加法推导等差数列前n项和公式.通过合作探究，激发学生的内部学习动机，努力解放思维禁锢，引发学生思考，激发学生发散性思维，并引导学生继续寻找等差数列前n项和公式的其他推导方式.

思维拓展1：深刻理解前n项和的含义和等差数列的通项公式，活用等差数列的通项公式构造新的推导方式，从而增强学生对相关知识的理解和应用，培养学生积极思考的习惯，让学生体会到研究的乐趣.

证明：∵Sn=a1+a2+…+an=a1+(a1+d)+(a1+2d)+…+[a1+(n-1)d].

【例2】等比数列前n项和公式是什么？怎样推导的？再想一想还有其他推导方法吗？(人教A版，数学必修5第二章数列第55页)

证明：∵当q≠1时，Sn=a1+a2+…+an=a1+a1q+a1q2+…+a1qn-1.

∴qSn=a1q+a1q2+a1q3+…+a1qn.

当q=1时，Sn=na1，故而得证.

∴Sn=a1+a2+…+an

思维拓展1：充分理解等比数列的通项公式和前n项和的定义，直接改写相关各项，并进行适当化简、变形与再造，从而归纳出下列方式进行推导.

证明：∵当q≠1时，

Sn=a1+a2+…+an

=a1+a1q+a1q2+…+a1qn-1

=a1+q(a1+a1q+…+a1qn-2)

=a1+q(a1+a2+…+an-1)

=a1+qSn-1=a1+q(Sn-an).

当q=1时，Sn=na1，故而得证.

思维拓展2:由于注意到思维拓展1中Sn=a1+qSn-1，联想到递推公式的特定式，从而构造新的等比数列，从而又可挖掘出新的证明方法——待定系数法.

当q=1时，Sn=na1.故而得证.

思维拓展3：充分理解和应用等比数列的定义，引导学生思考与联想，并对方程进行适当的整理、归纳和改写，从而借用“等比性质”来证明.这样既能较好地带动学生进行思维活动，又能较好地培养学生的化简和变形能力.

当q=1时，Sn=na1.故而得证.

在我们平时的教学实践中，对一些概念和公式进行必要的探索和挖掘，从不同角度分析其特性，引导学生对相应的式子进行必要的化简变形、整理归纳和比较发现，并积极联想和迁移，从而把一些孤立呆板的知识转化为有助于学生认知和把握的理性知识，这样会让学生更加深刻地体会到对知识的理解、应用和研究的乐趣，也让学生学会抓住问题的本质，提高他们举一反三的思维能力，进而培养学生对未知的探索能力．

二、再度借用教材例题、习题及变式题进行探究发现，培养学生分析问题和解决问题的多元思维.让学生真切感受这种自我探索、自我发现的学习方式，并在例题习题中体会和品尝新知的研究过程，从而形成对数学知识不断求索的自我需求.

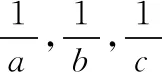
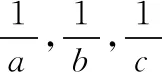
思维拓展1：紧扣a,b,c成等差数列这一条件，借用等差中项法进行直接推导.让学生体会数学问题解决的精髓——“看见已知想性质，看见结论想判定”.

证明：设a=b-d，c=b+d.

思维拓展2:充分理解数列是函数特例这一性质，从而应用数列的函数特征进行推导，这其实是最能揭示其本质的一个证明，同时也能使学生对知识有一次升华的体验.

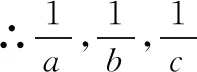
【例4】(教材习题变式训练)已知{an}是等差数列，Sn是其数列{an}的前n项和，S5=28,S10=36,求S15.

思维拓展1：结合等差数列前n项和公式的函数特征，采用待定系数法进行求解.这样能使学生在认识上实现跨越，并能培养学生函数、方程数学思想的应用意识，使相关知识得以提升.

思维拓展2：引导学生认真观察与分析，发现可用等差数列的性质:“等差数列中，Sn,S2n-Sn,S3n-S2n,…，成等差”，从而采用“等项片段和”直接计算出S15.

解：∵S5,S10-S5,S15-S10成等差数列.∴S5=28,S10-S5=8,S15-S10=-12.

∴S15=24.

思维拓展4：受思维拓展3的启发，可采用数列的函数特性，应用函数“图象法”来解决，真正理解和应用数列的函数特征.从而使知识再次升华.

∴从而S15=24.

这样，表面上看起来十分简单的一道题，经过不断探索发现，将数列与函数等知识充分融合，产生了多种有价值的解法.在这样一个探索过程中，学生的思维会得到充分地释放，在交流与展示过程中，也更能促使学生对相关知识有本质理解和综合应用,从而有效的提升学生的认知和钻研精神.

三、借用教材例题和习题的解法，寻求知识间“共性和个性”的关系，培养学生的思维迁移，使学生学会“反思性学习”和“创造性学习”，促使学生学会独立思考、迁移发散和综合应用.

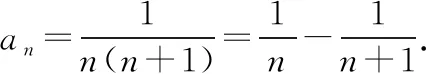
解法反思：我们可以带领学生积极总结和归纳,找出裂项过程的共性和个性，发现裂项相消在不同形式下的相消规律，理解裂项相消与相关参数的关系，体会相邻项的裂项相消和隔项的裂项相消在解决问题中的技巧.

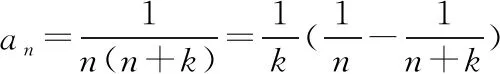
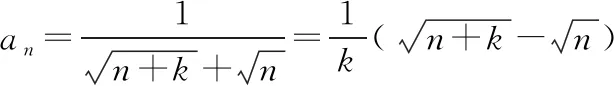
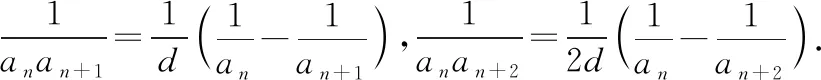
四、结束语

教材中像这样可以进行深入探索和拓展的题目还有很多，只要学生形成良好的研究习惯，善于钻研与反思，学会从不同角度不断发散和引申，可以总结出很多很好的方法和技巧，有助于学生进行更高效率的学习，真正提高学生分析问题和解决问题的能力，更好的培养学生的数学核心素养．