预制构件厂精益设计方案评价研究

孟子博，牛占文，刘超超

(1.天津大学 管理与经济学部，天津 300072；2.天津商业大学 管理学院，天津 300134；3.天津商业大学 管理创新与评价研究中心，天津 300134)

随着近几十年我国经济的发展，建筑行业保持了持续稳定的增长，但传统建造模式与环境保护之间的矛盾愈发突出，已经不能满足当前建筑业快速发展的需求。传统建筑亟需向新型的装配式建造模式转型[1]。装配式建造指在建造过程中，将部分建筑结构构件(预制混凝土构件)在工厂产出后，将其运到施工现场，按照一定的步骤、顺序将施工材料拼接起来，形成具有使用功能的房屋的建造过程[2]。目前，我国建筑业还没有形成一个标准化的建造体系[3]，装配式建筑普及程度不高。预制构件厂是装配式建筑产业供应链中提供构件的前端重要节点，是实现装配式建筑的基础，决定着实施装配式建造的成本和效率，对促进整个装配式建造的发展具有重要意义。传统建筑向装配式建筑进行转型也意味着更多的预制构件厂将建立起来，构件厂的设计无疑将成为一个值得研究的重点问题。

精益设计最早由天津大学齐二石教授于2009年提出，旨在在工厂初期规划与设计阶段就引入精益思想来确保在源头上消除浪费。国内外已有一些学者对如何将精益设计引入实际生产体系之中做了一些研究。王永升等[4]提出运用精益设计对工厂进行布局，给出运用仿真技术进行工厂精益设计的具体步骤。Sundin等[5]应用JIT技术对瑞典的垃圾回收站进行精益设计。 Weber[6]提出精益设计与传统设计的最大区别； Low等[7]从精益生产与传统工厂设计的集成理论入手，提出工厂精益设计的几点原则。但是已有研究多从将精益设计引入传统生产系统中进行研究，鲜有研究探索精益设计是否真正能达到精益设计的目标，缺乏系统性的评价指标，在预制构件厂精益设计方案评价的研究更是几乎空白。

针对以上问题，本文以预制构件厂生产系统的特点为切入点，确定预制构件厂精益设计方案评价指标。对于评价指标权重的确定则使用AHP-DEMATEL方法，有效提升权重的客观性，接着选用改进TOPSIS法进行设计方案的评价与选择，并用实际案例验证提出方法的合理性与有效性，为预制构件厂精益设计的导入及精益设计方案的选择提供了决策依据。

1 精益设计评价指标体系

预制构件厂精益设计方案的目标是从源头消除浪费，持续改善，为全面导入精益生产扫清障碍，最终实现可持续发展。可以说实施精益设计是传统设计的进一步延伸，是精益生产理论更深层次的升华[4]。与传统设计相比，精益设计的优势如表1所示。

表1 精益设计与传统设计区别Table 1 Differenceoflean design and traditional design

构件厂精益设计方案的评价，可以说是通过对此方案在构件厂实施后，能对整个构件厂所带来的整体精益化的提升效果判断，是为预制构件厂如何更大限度地提升精益效果做出科学的判断依据。对预制构件厂精益设计评价指标的科学、准确就决定了评价的结果，因此，建立一个科学、合理、完备的评价指标体系是构建预制构件厂精益设计方案评价的前提。

对于精益指标的选择已有相关学者做出了相关研究。Seyed Hosseini等[8]采用平衡记分卡的方法研究了汽车零件制造中的精益指标，从财务、流程、客户、员工和供应商5个视角出发提取了50多种精益指标。Vinodh等[9]提出具有30个精益指标的模型；Dennis[10]提出一个模型，主要考虑提供最短的交付周期，最低的成本和最高的质量给客户。Slack[11]根据质量、缺陷程度、时间和成本4方面来定义对客户的价值。其余文献不一一阐述，已有文献对精益指标的选取情况如表2所示。

结合众多学者的研究结果，可以看出资金、时间、质量、价值和生产能力是公认的精益程度的衡量标准的几个方面。

对于投资者或者股东而言，选择预制构件厂精益设计方案的目的是通过科学合理的设计，最大程度地降低工厂中的各种浪费，节约资金就意味着降低成本与消耗，以增强产品在市场中的竞争力。总体来说，在节约资金方面要考虑的因素有降低投资成本、物料搬运成本与库存成本，达到节省资金的目标。这就可以用节约资金的能力来表示。

而工厂的交付时间与构件的质量决定了其顾客满意度的水平，精益的目标之一也是缩短交付周期，使公司能够快速响应客户高水平的生产能力，代表着工厂要有着准时、均衡化的生产、较高的设备利用率、较高的大规模定制水平。这就可以用生产能力来表示。

表2 已有文献对精益指标选取情况Table 2 Literatures on the selection of lean indicators

产品的价值代表着工厂的生产能力，是工厂的生存之本，顾客都会希望被提供低成本高质量的有价值的产品，同时工厂应有足够的灵活性，可以提供柔性较强、较短时间内可以投入市场并且能够更快地交付给客户的产品组合，也就是工厂的交付能力。

国内的装配式建筑产业正在蓬勃发展，未来构件厂的生产工艺、布局、设备势必都要持续发展、持续改善以适应市场的发展与技术的进步，而工厂想要在快速变化的市场环境和激烈的竞争中生存下来的同时不断地提高节约成本能力、生产能力、交付能力，就要求工厂有高柔性的产线及可持续发展的能力。

简而言之，工厂的生产系统应当以消耗更少的资金、更短的交付时间、更高的质量及能带来更多的价值为目标，同时应持续不断地改进以满足上述目标。所以本文选取了节约资金能力、生产能力、交付能力和持续改善能力等4个方面来构建预制构件厂的精益设计评价指标体系，在遵循科学性原则、可量化原则、独立性原则、价值性原则、可持续发展原则的前提下，从这4个视角出发，进一步细分为12个三级指标，可以准确地反映精益设计相关活动内容。最终形成的评价指标体系，如图1所示。

图1 预制构件厂精益设计评价指标体系Figure 1 PC component factory lean design evaluation index system

1.1 定量指标

评价体系中定量评价指标总结如下。

1) 投资成本。

在预制构件厂精益设计体系中，投资可分为初期投建资金与日常运营成本两大部分，可表示为

式中，CT为 总投资成本；C1为初期投建成本；C2日常运营成本。C1可表示为

式中，C11为 厂房建设成本；C12为设备购置成本。C2可表示为

式中，C21为设备维护成本；C22为库存成本；C23为 信息化成本；C24为管理成本(一般来说管理成本与人员数量成正比关系，所以管理成本可以由工作人员数量来表示)；C25为财务成本。

2) 物料搬运成本。

一直以来物料搬运成本都占据了成本中花费较大的一部分，预制构件因其搬运的特殊性：构件体积一般较大，有的需要专门的固定支架，有的需要起重机加以运输，物料搬运成本更高，受到布局设计的影响更大，所以这也成为预制构件厂精益设计的一个重要影响因素。在预制构件厂生产系统内假定有n台设施，运输费用为

式中，Cij为单位距离单位物料运输费用；dij为设备之间物料运输距离；fij为设施之间物流量。

3) 库存成本。

在预制构件厂这个大的生产环境下，构件生产完毕之后将堆放在堆场，会占据较大的区域，所以在这里将库存成本用平均在制品库存水平表示为

式中，S为平均在制品库存量；Sp为p产品在制品库存量。

4) 均衡化生产。

在精益思想中，为了尽量减少生产过程中的库存与等待浪费，要尽力达到系统内各个工序间物流平稳、均匀、准时，也就是均衡化生产，均衡化水平可以由设备负荷平衡率来体现，可表示为

式中，Ti为设备i的负荷；Ttak为生产节拍时间。

式中，Xpki为0、1函数，指p产品第k道工序在设备i上生产时是1，否则是0；tpk为p产品第k道工序所耗费的时间；dij为 设备i到设备j之间的距离；vij为设备i到设备j之间的运输速度。

生产节拍时间可表示为

式中，T为总有效生产时间；Dp为p产品需求量。

5) 设备利用率。

指设备运行状态，要通过减少计划外停机时间来达到提高设备的利用率的同时减少设备故障率，可表示为

式中，ER表示设备利用率；E O表示设备开动时间；E L表示设备负荷时间。

6) 交付时间。

交付时间为原材料进入生产系统到生产完成并交付的时间。可以用平均生产周期来表示，即从原材料进入生产系统到生产完成所需的平均时间，本文主要指生产构件所需的平均时间[16]。平均周期越短，构件的供应就越是充分，项目按期完成的几率就越大，顾客满意度就会越高。可表示为

式中，TA为 构件平均生产周期；tfp为构件p生产结束时间；tsp为构件p开始时间。

7) 构件种类。

构件种类也可以理解为标准化构件的比例，装配式建筑能够产业化的一个重要前提是生产工业化，而生产能够工业化的核心要点是设计标准化。保证预制构件的标准化、规范化就能减少专用构件的数量、确保构件的准确性，就可以降低造价、节省成本。可表示为

式中，SPR为标准化产品比率；SP为标准化产品；p为所有构件种类；w1为标准化构件对整个预制构件厂产品体系的影响权重； SCi为第i件构件标准化零部件种类；Ci为第i件构件中所有零部件种类；w2为标准化构件对整个预制构件厂产品体系标准化的影响权重。

8) 构件质量。

主要指预制构件的制造合格率，也包括混凝土浇筑质量、结合面粗糙度的效果等。可表示为

式中，MPR为制造合格率；QP为制造合格的构件；P为所有构件种类。

9) 布局柔性。

也就是产线持续改善性能的能力，柔性可以分为设备、生产线柔性与整个生产系统3个方面的柔性来衡量[17]。设备柔性可表示为

式中，φ1代 表设备柔性；Fm代表设备m具备的生产加工构件的能力，以加工方法数目来计算；Lm代表整个预制构件厂生产体系中所具备的加工方法数目。产线柔性可表示为

式中，φ2代表产线柔性；ra代表生产线a所能生产的构件种类，a=1, ···,A；P代表整个预制构件厂生产体系内部具备的所有构件种类。生产系统柔性可表示为

式中，φ3代表整个预制构件厂系统布局柔性；Cc代表整个预制构件厂制造系统布局重构成本；Tc代表整个预制构件厂制造系统布局重构时间；CJ代 表预制构件厂制造系统投建成本；TJ代表预制构件厂制造系统最初投建时间。

1.2 定性指标

评价体系中定性评价指标如表3所示。

表3 定量指标解释及评价准则Table 3 Quantitative indicator interpretation and evaluation criteria

2 AHP-DEMATEL法确定权重

层次分析法(AHP)是学者Saaty为评价与分析问题提出的一种方法。该方法属于较为典型的一种系统评价方法，其优势包括灵活、系统与简洁，但还是存在一定的缺陷。国内最近几年已有学者开始借助 DEMATEL 来完善层次分析法。DEMATEL 法对某一因素作用于其他因素的影响 进行了研究，结合两种方法综合考虑因素相互间的影响与因素作用于上级指标的 影响，能够使得指标赋值更具客观性与科学性[18]。所以本文通过对上述2种方法进行结合，就整个指标体系当中各因素的层次关系与不同因素相互间的关联进行了系统考量，得出了优化之后的 AHP-DEMATEL方法。具体过程如图2所示。

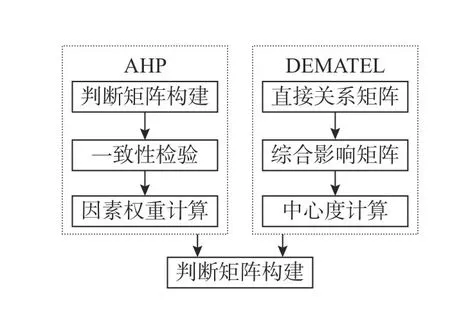
图2 AHP-DEMATEL法确定指标权重过程Figure 2 Process of AHP-DEMATEL method to determine the index weights

2.1 层次分析法确定指标基础权重

1) 构造判断矩阵。通过专家访谈对数据进行了收集，并两两比较上述元素，再以比例标度法为参照对重要性进行赋值，即对因素i与j比较后得出判断aij，则因素j与i比较得出判断aji=1/aij，从而建立一系列的判断矩阵A=(aij)n×m，其中，aij表示i元素和j元素相对于目标的重要性。对重要性的赋值，是由专家分别赋值再求其平均值。

2) 判断矩阵一致性检验。① 将判断矩阵的λmax值(也就是最大特征值)进行计算；② 按照式(16)对一致性检验的标度进行计算；③ 参照式(17)对随机一致性比率CR进行计算。通过表格可查出RI的值，通常CR比0.1更小则说明一致性检验获得了满意结果。

3) 元素相对权重的计算。通过特征根法进行计算，具体步骤如下：① 依照各行对A元素进行归一化处理；② 相加各行归一化之后所得向量；③ 用相加之后得到的向量与n相除便可得出元素的权重向量wi。

2.2 运用DEMATEL修正影响因素重要程度

1) 确定要素间直接影响程度。运用0-4标度法(如表3所示)对各影响因素的影响强弱进行两两比较，建立直接影响矩阵：

其中，bij表示因素层内i元素对j元素的影响强弱程度。

2) 规范化直接影响矩阵。利用式(19)计算规范化直接影响矩阵G。

3) 确定综合影响矩阵，利用式(20)计算综合影响矩阵T，其中I为单位矩阵，表达式(I−G)−1为表达式(I−G)逆矩阵。

根据综合影响矩阵T计算出指标间的影响度Fi、被影响度Ei、中心度Mi、原因度Ni。

2.3 计算综合权重

根据上文的计算目前已经有初步的各指标权重和指标间的互相影响的关系，再通过式(25)可得出指标的综合影响度，并将综合影响度Xi大于0.05的影响因素划分为关键影响因素，表达式为

3 基于改进TOPSIS法的构件厂精益设计方案评价

Hwang 等[19]提出一种通过计算评价对象与最优解与最劣解之间 距离来排序以逐渐靠近最优解的多属性决策方法，又被称为理想解近似法、理想解法。

传统TOPSIS法在实际应用中有以下3种缺陷：无法考虑各属性指标之间的相关度，受各属性指标量纲不同影响较大，无法考虑各评价指标因素重要性差异。本文考虑引入别的方法加以改进。

马氏距离[20]用来计算指标间的协方差距离，优点为此方法可以独立对指标的维度进行测量，不受坐标间的量纲影响并且排除了变量间相关性的干扰，具体公式为

式中，X为一个随机向量；Y为X的均值向量；∆为属性指标间的协方差矩阵，一般来说当属性指标间量纲有互相影响时需要对指标进行归一化处理，但由于 ∆对于线性变换是不变的，所以不受到属性指标量纲影响，便不需要对原始决策矩阵归一化处理。但如果协方差矩阵为奇异矩阵，那么∆−1就不存在，从而无法计算。为了解决这个问题，就需要解决原始协方差矩阵是奇异矩阵的问题，此时广义马氏距离的出现恰好解决了这个问题，其计算公式为

式中，用 ∆+λI代替了原始协方差矩阵∆，其中λ值选取方法为

λ0∆ 10−3

式中，是为协方差阵 的所有特征值比 大的特征值最小值。但是广义马氏距离没有考虑到指标间重要性的差异，关宏艳[21]提出采用加权广义马氏距离改进传统的马氏距离，将权重引入加以综合考虑。

式中，wn为指标权重。由于需要对各指标间的相关性及重要性进行考虑，并对不同量纲和相关性加以解决，这样才能消除对马氏距离对决策结果的影响以及协方差矩阵不可逆的问题。鉴于以上优点，本文选用加权广义马氏距离对TOPSIS法加以改进。

因此基于传统TOPSIS法基础上融入加权广义马氏距离后的计算过程如下所示。

1) 构造有m个评估对象，n个评估指标的初始决策矩阵

2) 确定正理想解Z+和负理想解Z−：

式中，T1为 效益型指标(数值越大越好)；T2为成本性指标(数值越大越好)。

3) 计算各评估对象Zi到正、负理想解的校准马氏距离和

4) 计算每个评估对象与理想解接近度Ci：

5) 给评估对象排序。

对求出的Ci进行排序，贴近程度Ci越接近1，表示越接近正理想解，评估对象越接近最优。

4 案例分析

某一新建预制构件厂正准备组装产线，现需选择合适的精益设计方案进行制造系统组建，初步分析后预制构件厂的管理层针对不同的设备选择初步形成了3个备选方案进行方案的评价选择。由于评价指标有定量与定性两部分，所以分开计算。定量指标由MATLAB2010B与FLEXSIM3.0软件上进行计算仿真后得到了在制品库存与平均生产周期等基本信息，所获得数据如表4所示。定性指标的计算采用模糊评价方法，首先通过专家打分得出评价值，然后计算隶属度，用来矫正专家打分的偏差。最后并采用中位数方法对专家评语级别V={优，良，中，差}进行量化处理，本次评级中的优良中差分级对应的值分别为V={93，83，68，30}。最终经过定量与定性处理后得到所有方案的指标评价计算结果。

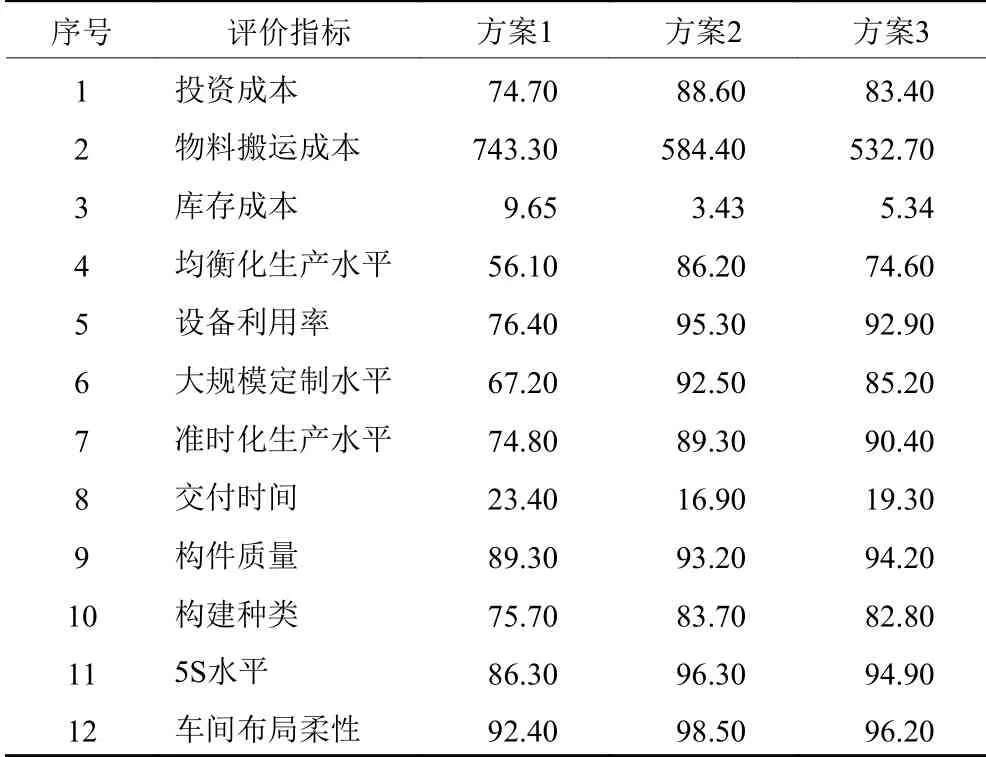
表4 方案评价指标参数Table 4 Parameters of the program evaluation index

4.1 评价指标权重的确定

4.1.1 运用AHP分析影响因素的基础权重

首先，构建判断矩阵，然后针对各因素层指标构建了互补判断矩阵，经过计算后可得各指标因素权重关系如表5所示，并且结算结果均满足CR＜0.1的要求，通过一致性检验。

表5 预制构件厂精益设计指标初始权重Table 5 Initial weights of PC component factory lean design index

4.1.2 运用DEMATEL修正影响因素重要程度

首先，建立直接影响矩阵Xd，如表6所示。

表6 直接影响矩阵Table 6 Direct influence matrix

根据直接影响矩阵可以得到综合影响矩阵，从而进行影响度与最终权重的计算，如表7所示。

表7 精益设计指标的最终权重Table 7 Final weights of lean design indicators

4.2 方案的评价与选择

根据上述计算结果与式(31)和式(32)可以计算正、负理想解，并采用式(33)、式(34)与式(35)计算方案与正、负理想解之间的距离与贴进度，计算结果如表8所示。

根据本文所提出的计算方法，对备选方案做出的排序为：方案2＞方案3＞方案1。方案2整体呈现出了最优的结果，从贴近度来看，方案2有着最贴近最优解的距离，因此选择方案2来进行构建生产系统。从各属性权重及评价值来看，均衡化生产、准时化生产、交付时间与构件质量等这几个权重较大的属性评价值均较优，因此方案2优等性较明显，计算结果基本符合实际，比较合理。

表8 备选方案的距离与贴进度Table 8 Distance and progress of options

5 结语

本文以建造预制构件厂生产体系精益设计入手，提出了由准则层4个视角、因素层12个评价指标组成的预制构件厂生产体系精益设计评价指标体系，然后采用AHP–DEMATEL确定权重及加权广义马氏距离改进的TOPSIS方法对多方案进行计算与决策，最后以某预制构件厂为例验证了评价方法的科学性与合理性，可为构建预制构件厂精益设计评价指标体系及精益设计方案的评价与选择提供借鉴。本文得到了一些有价值的结论，但仍存在许多不足，需后续深入研究，如评价体系可以进一步完善；研究的案例较少，后续研究可以增加样本量。