危化品事故连续消耗型应急物资调度模型
2020-11-15卢建锋牟瑞芳赵佳虹王小霞
卢建锋,牟瑞芳,赵佳虹,王小霞
(1.西南交通大学 交通运输与物流学院,四川 成都 610031;2.广东工业大学 土木与交通工程学院,广东 广州 510006)
危化品在其生产、储存以及使用过程中极容易发生事故。在过去的几十年里,危险品事故频发,给自然环境和人类生活带来严重危害。在危化品事故的应急救援中,除了需要一次性消耗的应急物资,如衣服、帐篷外,还需要连续消耗的应急物资,即应急活动中需持续不断供应的资源类型,比如燃气、食品、医药等。一直以来,连续消耗型物资调度问题得到许多学者的关注[1-2]。刘春林等[3]分析了应急物资调度系统多点出救的特点,引入了连续可行方案的概念,并提出以应急开始时间最早为目标的数学模型。潘郁等[4]研究了连续性消耗应急物资的调度,从应急活动成本和受灾损失2方面考虑,构建了总成本最低的应急物资调度模型。魏国强等[5]建立规划模型,解决了多应急点连续消耗应急物资调度预案的制定问题。郑昊等[6]假设应急资源的消耗速率为非负可积函数,构建了应急时间最早为目标的连续型应急物资调度模型。张力丹等[7]将灾民安置与物资运输一体化规划,以施救不及时损失和应急系统施救成本为优化目标,构建连续消耗应急物资调配模型,并用遗传算法和序列线性规划算法相结合来求解模型。在应急物资调度优化目标方面,目前国内外研究较多的包括: 出救点最少、应急时间开始最早、最短运输时间和最小运输成本等[8-11]。
以上关于连续消耗应急物资调度的研究主要考虑调度效率、成本以及受灾损失等,并不完全适用于危化品事故应急物资调度。因为对于危化品事故而言,发生事故会对周边污染环境,有毒气体将扩散到道路网中形成毒性负荷,在调度时应该考虑毒路径毒性负荷,本文在现有研究基础上,针对危化品事故应急物资调度特征,构建以缺货损失最小、调运时间最短和调运毒性负荷最小为优化目标的连续消耗应急物资调度模型,并采用NSGAⅡ遗传算法求解模型,得出多种可供参考的应急物资调度方案,采用逼近理想解的排序方法选择推荐方案。
1 问题描述及模型建立
1.1 问题描述
设危化品事故只有一个受灾点S,共需要m种连续消耗型应急物资,周边有n个应急中心点能向受灾点S供应应急物资。每个应急中心到受灾点之间有多条推荐路径,每条路径时间和毒性负荷均已提前预测得到。要求给出一个应急中心应急资源调度方案,包括确定应急中心点发出的应急物资数量及其所选择路径。要求调度模型尽量实现以下目标:1) 受灾点缺货损失最小,即使得受灾点因物资缺乏导致的损失最小;2) 完成应急调度运输的所耗时间最短;3) 调度毒性负荷最小。
1.1.1 假设条件
模型建立的假设条件为
1) 各种类型物资都可以混装在一辆货车;
2) 受灾点的多种物资的消耗速度是确定不变的;
3) 每个出救点运力充足;
4) 运输过程中不同路径的运输时间和运输风险是己知的。
1.1.2 符号说明
I为出救点集,i∈I;
J为资源种类集,j∈J;
K为出救点到受灾点的路径标号集,k∈K;
Ai为 第i个出救点(i=1,2,···,n);
S为受灾点;
hik为从出救点i出发的第k条路径;
wik为出救点i到受灾区第k条路径的环境风险值,用路径毒性负荷来表示,计算方法见文献[12];
Tik为出救点i到受灾区第k条路径的行程时间;
yik表示出救点是否选择第k条路径,yik=1时为选择,yik=0时不选择;
G0为标准货车载重量;
Ni为出救点i派出的货车数量;
vj为应急活动开始后j类物资消耗速率;
ti为从出救点i到达受灾点花费的时间;
t0为救援的机会时间;
l为各出救点车辆到达受灾点的顺序,l=1,2,…,n;
t(l)为第l个到达受灾点所用的时间;
T为应急活动结束时间;
dmaxij为 出救点Ai处第j类物资最大可供应量;
dj(l)为t(l)时刻到达受灾点的j类应急物资数量;
lj(t)为t时刻受灾点第j类应急物资存量;
Fj为受灾点因j类应急物资缺失而导致的单位时间损失费用;
Ej0为 从机会时间t0到第1个出救点物资到达时,因j类应急物资缺失导致的损失费用;
Ejl为第1个出救点物资到达以后,因j类应急物资缺失而导致的损失费用;
Ej为受灾点因j类应急物资缺失而导致的总损失费用;
xij为 出救点Ai提供的j类物资量。
1.2 应急物资缺货损失计算方法
在受灾点应急物资连续消耗的情况下,受灾点的物资库存量如图1所示。
引入一个判断变量Ril,设定Ril=1时为应急中心i在t(l)时 刻为受灾点供货,Ril=0时为其 他情况,则即n个应急中心有且只有一个是第l个到达受灾点。
t(l)第l个到达受灾点的时间只能是n个应急中心中一个。

图1 第j类应急物资连续消耗下库存量变化图Figure 1 Change chart of inventory under continuous consumption of category j emergency material
x(l)第l个到达受灾点的物资只能是n个应急中心中的一个。
从事故发生时刻t=0到机会时间t0的损失不可避免。应急物资缺失导致受灾点的损失费用计算方法如下[13]。
事故发生时,从机会时间t0时到第1个应急中心物资到达时刻t(1),这段时间内受灾点物资库存量必然缺失,因此得出第j类物资缺失的损失费用为

为不失一般性,设t(k)≤T,且t(n+1)=T,则 在t(k)时刻受灾点j类物资库存量为

如图1所示,存在t(F)∈[t(k),t(k+1)],且t(k))=0时,受灾点第j类物资有部分存余,但却无法满足整个周期 [t(k),t(k+1)]的需求,物资存在部分缺失。此时,有且有0 ≤Ij(t(k))≤vj[t(k+1)−t(k)],得第j类物资缺失的损失费用为

其他情况下,Bjk=0。
因此,应急物资缺货损失费用按以下2种情况处理。
1)Bjk=0,第i时刻受灾点各类应急物资都充足,即缺失量为0。则,因第j类应急物资缺失导致的损失费用只是从机会时间t0时到第一个应急中心物资到达时刻t(1)的时间段内的物资缺失。第j类物资缺货损失费用为

2) 当第j类物资应急物资在周期 [t(k),t(k+1)]内缺失,即存在t(F)∈[t(k),t(k+1)],使得

第j类物资缺货损失费用为

1.3 模型建立
要求给出应急物资调度方案{dij},具体包括参与应急的应急中心选择及其提供的物资数量。模型建立如下。
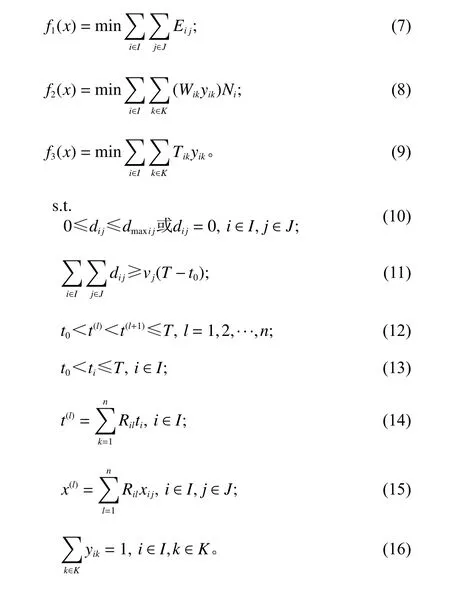
Ni表示某事故阶段某应急中心要派的货车数量,其值为该点派出的总货物质量除以单位货车载重量向上取整数。
式(7)表示受灾点缺货损失最少;式(8)表示使物资调运过程中环境风险最小;式(9)表示应急物资运送到受灾区的总调运时间最短;式(10)表示应急中心提供的物资数量介于d0和dmaxij之间,或能提供的物资数量为0;式(11)表示各类物资总供应量大于需求量;式(12)表示t(k)不 小于机会时间t0,也不大于应急结束时间T;式(13)表示ti大于机会时间t0,小于应急结束时间T;式(14)表示第k个到达受灾点的时间只能是n个应急中心中的一个;式(15)表示第k个到达受灾点的物资只能是n个应急中心中的一个;式(16)表示每个应急中心到达受灾点选择的路径有且只有一条。
2 算法设计
由式(7)、式(8)、式(9)及其约束条件可知,模型属于非线性多目标优化问题,存在多个Pareto解,且需要结合决策者的偏好对解进行选择。考虑求解效率,可采用非劣分层遗传算法(NSGAⅡ)求出模型Pareto最优解集,构成决策矩阵。在选择最优解时,用信息熵法[14]确定3个目标属性的权重,最后采用逼近理想解的排序方法(TOPSIS)对Pareto最优解排序,依据决策者偏好选出最优解。
2.1 非劣分层遗传算法(NSGAⅡ)
非劣分层遗传算法(NSGAⅡ)是目前求解多目标问题应用较好的一种算法。NSGAⅡ在NSGA算法基础上加入精英策略、快速非支配排序策略以及密度值估计策略。借鉴NSGA-Ⅱ算法中的选择机制,对交叉和变异算子进行适当修改。算法步骤如下[15]。
步骤1初始化种群规模 Popsize,对最大迭代次数、交叉概率和变异概率进行设置,计数器gen=1。
步骤2生成满足约束的个体Popsize个,计算每个个体的目标函数值,对所有个体进行非支配排序,生成父代种群。
步骤3利用锦标赛选择、多点交叉和实值变异方法,对父代进行遗传操作,生成临时种群。
步骤4判断临时种群的个体满足约束条件否,找出不满足这些约束的个体,产生满足这些约束的相同数量的个体替代,得出子代种群,计算个体后代的目标函数值。
步骤5将父群体和子群体合并,并进行非支配排序,将Popsize值最高的个体作为父代种群,gen=gen+1。
步骤6如果 gen≤Maxgen,转入第3步,否则结束。
以上算法的关键部分操作说明如下。
1) 染色体的编码。用1个染色体来表示从应急中心Ai至受灾点S的物资调度方案。染色体的每个基因对应每个应急中心各类物资配送到受灾点的数量及该应急中心所选路径。
2) 适应度函数。适应度由目标函数值决定,每条染色体都具有3个适应度值f1、f2和f3。
3) 遗传操作。选择: 根据快速非支配的排序以及拥挤距离大小,采用锦标赛法做选择。交叉和变异: 采用遗传算法的多点交叉算子,加快了求解空间的搜索速度,避免了早熟收敛。利用实值变异和区域扫描限制变异范围,使新个体无法跳出解空间中相应解。
2.2 逼近理想解的排序方法(TOPSIS)
TOPSIS方法通过比较和理想解的相近程度,计算与理想解和负理想解的距离来对方案排序,计算流程如下[16]。
1) 用向量规范法得出规范决策矩阵。假设有模型有n个多目标属性,m个决策方案。原决策矩阵Y={yij}, 规范化后的决策矩阵为Z={zij}, 则

2) 构成加权规范矩阵。
设多属性的权向量w={w1,w2,···,wn}T,则

3) 求理想解x+和负理想解x−。设理想解x+的第j个属性值为设负理想解x−的第j个属性值为则正理想解为为效益型属性),或(j为成本型属性)。负理想解为为成本型属性),或(j为效益型属性)。
4) 计算各备选方案到理想点和负理想点距离。备选方案到理想点距离为

备选方案到负理想点距离为

5)计算各方案排队指示值(综合评价指数)。

6)根据Ci值由大到小排列方案的优劣次序。
3 数值与算例分析
3.1 算例数据
设某危化品仓库发生泄露并引发爆炸等事故,仓库周边一定范围成为受灾点。现急需4种应急物资,可从5个应急中心点安排物资调度。受灾点和各应急中心点的分布如图2所示,各应急中心到受灾点的路径的环境风险值和时间如表1所示,各应急中心物资存有量如表2所示。各类应急物资的需求总量为X=(40,30,40,45) t,各类应急物资的消耗速率V=(3,5,4,1) t/min,各类物资缺失后的单位时间损失费为F=(7,2,9,5) 元/min,应急救援活动的终止时间T为80 min,标准货车载重设定为18 t。假设到达受灾点的不同路径时间和毒性负荷提前计算得到,要求在满足受灾点应急物资需求的条件下,求出最优调度方案。
3.2 求解结果

图2 危化品事故受灾点和救援点位置示意图Figure 2 Schematic map of disaster site and rescue site of dangerous chemicals accident

表1 各应急中心点到受灾点的路径相关数据Table 1 Path-related data from emergency centers to the disaster site
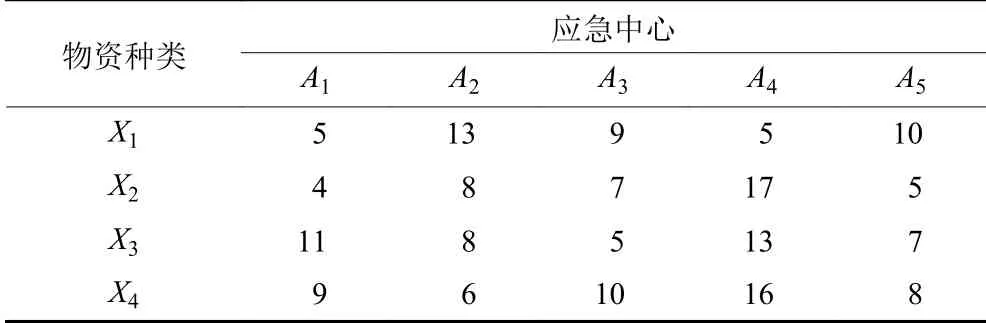
表2 各应急中心物资数量Table 2 Quantity of material at material emergency center t
在Intel Core Intel Core i5-337U@1.8 GHz处 理器,8 GB 内存的计算机上用Matlab语言编写NSGAⅡ算法程序对算例仿真。多次测试后,参数确定为:初始种群数量为500,交叉概率为0.8,变异概率为0.04,最大进化代数为1000。模型目标函数共求得52个Pareto解,如图3所示。

图3 NSGAⅡ算法帕累托最优解示意图Figure 3 Schematic diagram of Pareto optimal solution for NSGA II algorithm
用这些解构造52×3的决策矩阵。先利用信息熵法计算得缺货损失、环境风险、调运时间属性的权值向量为w=[0.04,0.86,0.01]。
再运用TOPSIS法,对52个Pareto解进行排序,排序第1的解为满意解。该解作为应急物资调度推荐方案,如表3所示。方案的缺货损失、环境风险、调运时间属性值向量为P=[107150,850,40]。

表3 应急物资调度推荐方案Table 3 Recommended schemes for emergency material dispatching
此外,缺货损失最小方案如表4所示。该方案的缺货损失、环境风险、调运时间属性值向量为P=[104510,2140,40]。
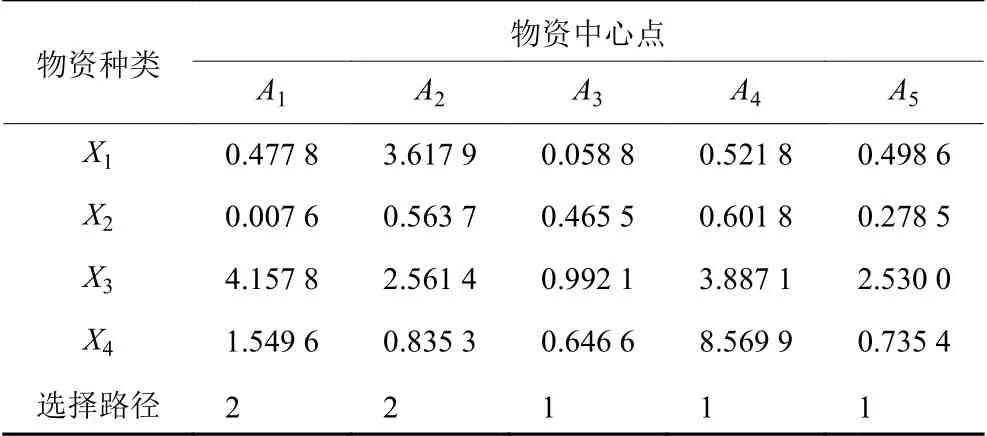
表4 缺货损失最小方案Table 4 Shortage loss minimum scheme
将推荐方案和受灾损失最小方案对比,结果如表5所示。可发现推荐方案的环境风险值比受灾损失最小方案节约近一倍,而受灾损失相差很小,行程时间相同。可见推荐方案有较大的优势,也说明了算法的合理性。

表5 两方案目标值对比表Table 5 Target value contrast table of two schemes
4 结论
危化品事故常常伴随毒气泄露,污染周边道路网。进行应急物资调度时考虑路径毒性负荷,能减少调度工作人员二次伤害。本文针对危化品事故应急物资调度的特点,建立了危化品事故连续性消耗的应急物资调度优化模型,以缺货损失最小、调运时间最短和调运总环境风险最小为优化目标,采用NSGAⅡ遗传算法求解,得出多种可供参考的应急物资调度方案,采用逼近理想解的排序方法选择推荐方案。通过算例分析,将推荐方案和受灾损失最小方案对比,发现推荐方案的毒性负荷比受灾损失最小方案小近一倍,而受灾损失相差很小,调运时间相同。说明推荐方案有较大的优势,也说明算法合理可行。
