基于贪心遗传的地下物流节点选择规划研究

2020-11-15王苏林邱菲尔刘川昆王芷芸

工业工程 2020年5期

王苏林，邱菲尔，陈凡，刘川昆，鹿腾，王芷芸

(1.西南交通大学希望学院轨道交通学院，四川南充 610400；2.西南交通大学交通运输与物流学院, 四川成都 611756；3.西南交通大学土木工程学院, 四川成都 610031；4.西南交通大学信息科学与技术学院，四川成都 611756)

近年来，随着城市化进程的不断加快，城市交通拥堵、环境污染等问题严重制约了生态、和谐、美好城市的发展[1]。通过大量的研究与实践证明，要解决城市交通拥堵问题，一方面需要扩张传统路网容量，另一方面需要结合地下空间开发利用，将物流系统逐步转向地下[2-3]。美国、德国等国家针对地下物流系统展开了一系列的研究开发和实践应用，我国在上海展开了地下集装箱物流系统初探[4]。

基于此，地下物流应运而生。马祖军[5]基于城市地下物流系统发展现状，对城市地下物流系统设计的主要步骤进行了研究。闫文涛等[6]验证了双层规划模型在地下物流节点选址应用中的实用性和科学性。易美等[7]利用分层分级配送构建思路，建立了一类城市地下物流网络规划模型。曾令慧等[8]建立了城市地下物流网络优化模型，并采用基于遗传算法进行求解。张培林等[9]建立了有关多个配送中心的选址模型并通过启发式算法进行优化求解。戢晓峰等[10]综合考虑配送企业的配送成本、环境成本及配送时间，构建了双层规划模型。谢雪姣等[11]基于混合整数线性规划构建了城市地下物流系统。李明等[12]针对多物流配送中心的选址布局提出了优化模型。

上述研究成果针对城市物流网络节点选址、路径优化进行了初步研究，但是很少从物流节点的数量及节点转运率层面进行研究。本文在引入集合覆盖思想的基础上，建立以物流节点数量最少及物流节点转运率最低为优化目标的双层多目标规划模型，并结合贪心算法和遗传算法，设计一种贪心遗传算法对问题进行优化求解，确定地下物流节点，为地下物流网络优化提供依据。

1 问题背景

现有某地区交通货运区域划分图及相应的货运OD流量矩阵(表1)、各区域中心点及区域面积、各区域交通拥堵指数(表1)，为缓解该地区交通拥堵现状，降低物流运输成本，拟建城市地下物流网络，实现该地区物流运输的多式联运[13]。

地下物流网络由一级、二级节点和节点间地下通道构成，各级节点均与地面衔接并实现多式联运。一级节点与物流园区相连，并可跨区域调运货物，一级节点之间连通，二级节点与非本区域一级节点仅通过本区域一级节点连通。

针对该问题，假设如下。

1) 假设进出4个物流园区的货物尽最大可能放入地下运输；

2) 为简化计算，将交通货运区域中心点当作物流需求点；

3) 所有节点的服务半径在3 km范围内自由选择，节点间距离不受限制[14]；

4) 货物从二级节点至地面后采用人力或小型车辆在节点服务区域内运输，可认为不影响交通。

表1 需求点货运流量及交通拥堵系数Table 1 Traffic flow and traffic congestion coefficient

2 集合覆盖模型

集合覆盖问题[15]是组合最优化和理论计算机科学中的一类经典问题，要求以最小的代价将某一集合利用其若干子集加以覆盖，其数学模型由Toregas等人最早提出，并最初应用于消防站、救护车等应急服务设施的选址问题上[16]。

在地下物流系统物流节点选择的问题中，运用集合覆盖模型确定物流节点的数量与位置，从而实现使用最少的物流节点来满足所有需求点的需求量。集合覆盖模型实质为一个以物流节点数量最小为目标函数、物流节点能够满足所有需求点的需求量为约束条件的优化模型。

假设现有n个物流需求点，其集合为Sj={e1,e2,···,en}，S1,S2,···,Sm为S的所有子集，若J⊆{1,2,···,m}，且则称S={Sj}j∈J为S的一个集合覆盖。

对于每个子集Sj(j=1,2,···m)，引入决策变量

其中，j∈J表示节点j为需求点集合Sj提供服务，此时将节点j称为物流节点。

模型目标为选取最少的物流节点数，即

每1个需求点至少需要被1个物流节点所覆盖，则存在约束条件

建立集合覆盖模型如下：

在集合覆盖模型中，各需求点代表着各交通货运区域，需求量即为各货运区域运输的货运量。根据实际情况，地下物流节点的选择还应考虑到节点分级、转运率等指标以及物流节点的最大供应能力、服务范围等问题，因此，需要在经典集合覆盖模型的基础上进行延伸，重新确定决策变量、目标函数以及约束条件，建立改进的地下物流节点选择模型。

3 物流节点选择模型建立

考虑物流节点数量及物流节点转运率，将地下物流网络节点选择看成一个双层多目标规划问题，分别对上下层规划的目标函数、决策变量、约束条件进行讨论，最后对各层的讨论结果进行归纳总结，得到最终地下物流网络节点选择模型，如图1所示。

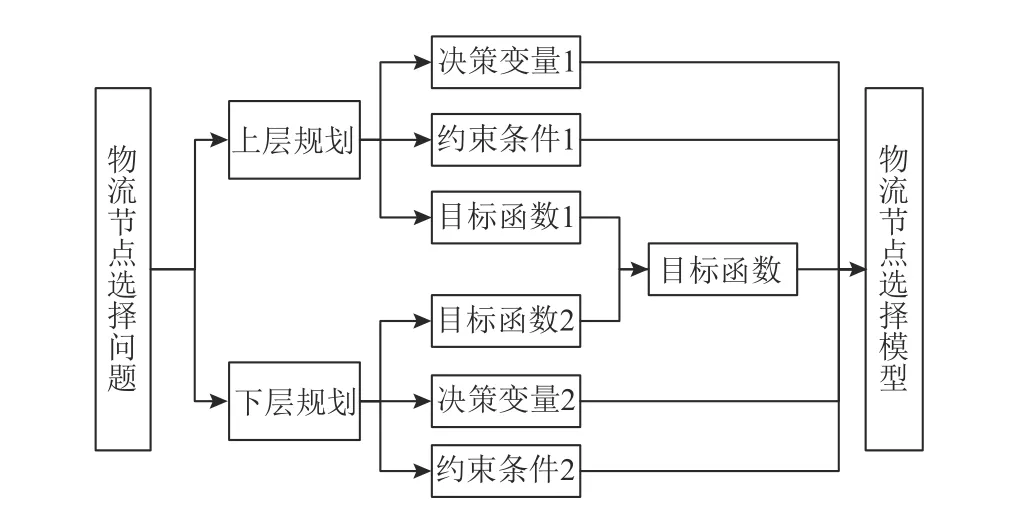
图1 节点选择模型结构Figure 1 Node selection model structure

3.1 节点选择模型上层规划

在确认了1个集合覆盖S={Sj}j⊆J后，对于每一个Sj(j⊆J)，1个物流节点负责了集合中各需求点的需求。以物流节点到达其覆盖的需求点路径和最小为原则，求得各物流节点的位置(Ojx,Ojy)以及服务半径rj。如图2所示，现有系列需求点ei组成点集其各点坐标为其区域物流节点的位置需满足其到各需求点的距离和最小，即为以下目标规划模型的最优解。

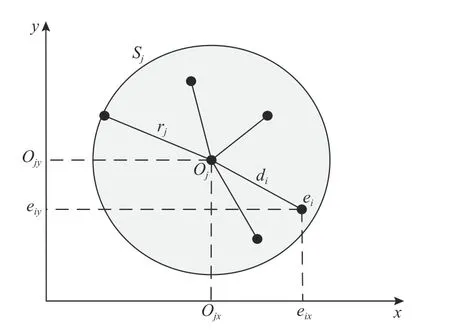
图2 节点位置与服务半径示意图Figure 2 Node position and service radius

确定了物流节点的位置后，其服务半径为该物流节点到需求点的最大距离，即

因此，以物流节点数量最小为优化目标，考虑物流节点的服务范围、最大供应能力等约束，求得1组物流节点能够完全覆盖整个区域的货运量。

1) 每个需求点都至少被1个物流节点所服务。

对于每1个需求点ei，肯定包含于1个或多个集合覆盖的子集Sj(j⊆J)中，即

式中，aj为节点j为需求点集合Sj提供服务的布尔变量，j∈J，其值为1，否则为0。

2) 各需求点的供需相等。

对于每一个需求点ei，各节点对其服务量之和应该与其需求量相等，即

式中，hij为第j个节点对第i个需求点的实际服务量(货运量)；bij为节点服务范围的布尔变量，第j个节点与第i个需求点存在服务关系，其值为1，否则为0；wi为各需求点的总货运量。

3) 节点的服务能力限制。

一级节点从地面收发货物总量上限为4000 t，二级节点从地面收发货物总量上限为3000 t，若以cj统一表示节点的服务能力限制量，则有

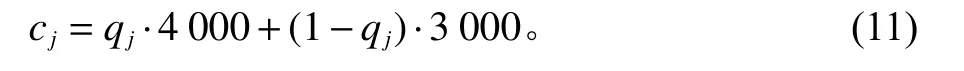
对于每1个物流节点j，其总服务量应小于其服务能力限制量，即

式中，qj为一级节点布尔变量；j为一级节点，其值为1，否则为0；一级节点的点数为二级节点的点数为

4) 物流节点的服务半径限制。

对于第j个节点，若其为物流节点，则服务半径在3 km的范围内，即

5) 一级节点个数限制。

一级节点与物流园区相连，且物流园区经由最近的一级节点转运至其他所有节点，即每个物流园区仅对应1个一级节点(选择其最近的一级节点进行连接)，即一级节点的总数固定为4个

综上所述，考虑将节点数控制在最低的上层规划模型如下。

3.2 节点选择模型下层规划

设第i号一级节点的转运率为φi；第i个物流园区的总出货量为Li；第i个物流园区通过对应的一级节点发往二级节点j的货运量为Tij。第i个物流园区与其隶属节点关系连接如图3所示。

图3 物流园区与节点连接示意图Figure 3 The connection of logistics park and node

一级节点与物流园区相连，一级节点之间连通,二级节点通过本区域一级节点与其余一级节点连通，即，对于第i个物流园区，1个一级节点与其直接相连，一系列二级节点通过此一级节点与其间接相连。zij为一级节点与物流园区及二级节点的连接情况布尔变量，若第j个节点与第i个物流园区直接或间接相连，其值为1，否则为0。

根据zij、qj的值便可确定节点的分级以及连接情况，若zijqj=1，则第j个节点为与第i个物流园区连接的一级节点。

由于转运率越低，工作量越小，因此，将一级节点的平均转运率最低作为下层规划的优化目标。对于任意一个物流园区，其只与1个一级节点直接相连，且对于任意1个物流节点，其有且只与1个物流园区直接或间接相连。下层规划具体模型如下

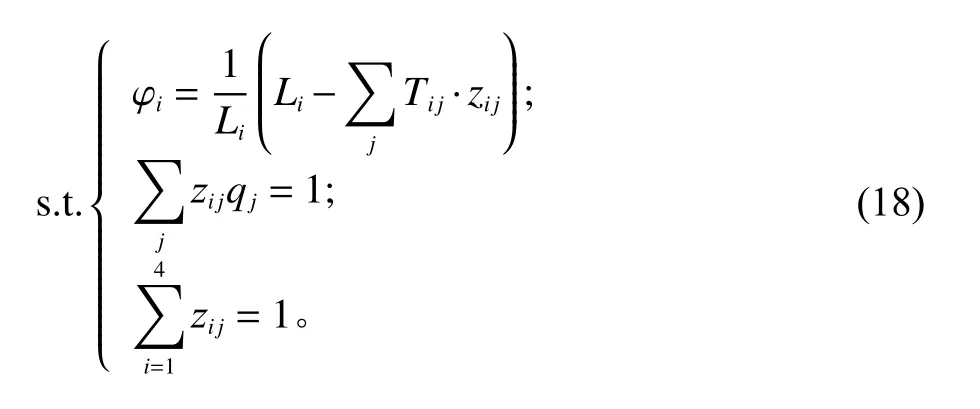
4 物流节点选择模型求解

4.1 下层规划模型求解算法

根据上述模型的构建，以平均转运率最低为优化目标的节点选择下层模型求解算法如下。

1) 将节点按照地域分为4个集合，每个集合内的点与最近的物流园区连通，计算转运率φ。

2) 随机选取1个点。

3) 将选中的点依次放入其他的集合中，计算该节点划分情况下的转运率，选取转运率最低的集合划分情况为最优情况。

4) 若达到最大迭代次数，进入5)；否则更新状态，转至2)。

5) 对于每1个集合，选取中心点作为一级节点。

4.2 双层规划模型求解算法

为实现对模型结果的全局搜索，采用遗传算法[17-18]求解双层规划模型，在下层模型的基础上进行选择、交叉及变异等操作，最终得到节点选择双层规划最优解。具体操作步骤如下。

1) 初始化种群。采用贪心算法得到局部最优解作为初始种群。为了提高求解速度，不妨将服务节点设置在某一需求点处，在后续步骤中进行更细致的优化。算法流程图如图4所示。

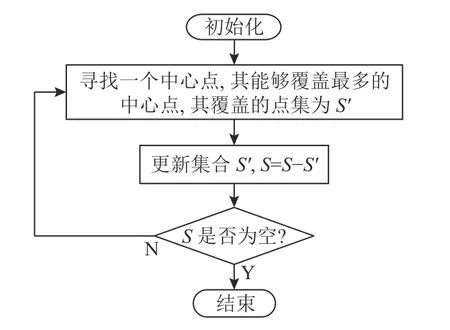
图4 贪心算法流程图Figure 4 Greedy algorithm flow chart

2) 编码方式选取。由于问题的解空间连续，为改善遗传算法的计算复杂性，采用长度为10的二进制编码串来表示模型中的布尔变量，采用实数编码来表示节点坐标、货运量等。

3) 适应度函数确定。由于问题为多目标规划，因此采用线性加权对目标函数进行简化，然后取其倒数作为适应度函数。对于某一个体，根据下层规划模型，可以求出其目标函数的值，其中F1、F2分别为上层规划及下层规划的目标函数。

式中，N为一个权重系数，取为20。

4) 选择操作。采用轮盘赌进行选择，在此情况下个体t被选中的概率可以表示为

5) 交叉操作。对染色体的二进制部分与实数部分分别进行交叉操作。

① 对于实数部分，第u个染色体Au和第v个染色体Av在t位的交叉方法为

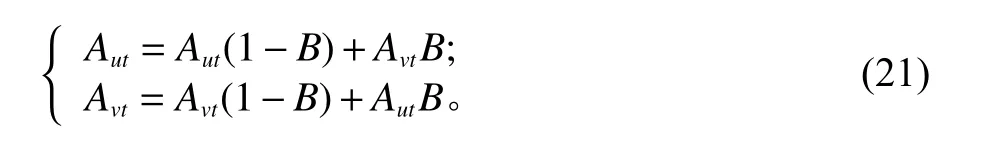
其中，B为[0,1]区间的随机数。

② 对于二进制部分，兼顾到收敛的速度和稳定性，选取3点交叉的方法，即通过随机数选取染色体的3个位置，再对2条染色体在这3个位置上的值进行交换。

6) 变异操作。对染色体的二进制部分与实数部分分别进行变异操作。

① 对于实数部分，第l个个体的第t个基因Alt进行变异的操作方法为

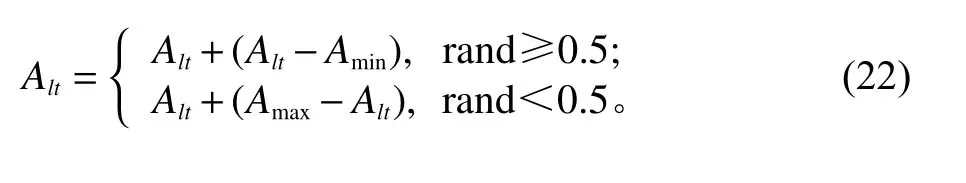
其中，Amax是基因Aij的上界；Amin是基因Aij的下界；rand为[0,1]区间的随机数。

② 对于二进制部分，选取3点交叉的方法，即通过随机数选取染色体的3个位置，再对染色体在这3个位置上的值进行随机取值。

5 求解分析

基于上述贪心遗传算法[18]，通过Matlab编程求解得到该地区每个物流需求点 Ci的总货运量及各个物流园区Ai分别对该物流需求点的货运量。图5为所有物流园区对各需求点的总货运量，由图5可知，需求点C1、C3、C5、C9、C11、C17、C18、C19、C20的货物需求量较大，均在1450 t以上，而其他需求点货物需求量相对较小。

图5 所有物流园区对各需求点的总货运量Figure 5 Total cargo volume of all logistics park for demand points

图6为各个物流园区对需求点的货运量，由图6可知，4个物流园区对所有需求点的总货运量偏差不大，对各个需求点的货运量均在400 t左右波动，其中A2—C6、C7、C9的货运量较其他需求点明显增大，主要是由于这3个需求点的位置与A2物流园区的距离较近所致。

图6 各物流园区对需求点的货运量Figure 6 Cargo volume of each logistics park for demand points

针对问题中的20个物流需求点，从路径优化及节点转运率的角度考虑，服务节点及物流需求点均遵循就近原则，即每个物流需求点会尽可能从最近的服务节点获取物流，而每个服务节点为降低转运率会尽可能地服务最近的需求点。通过Matlab编程求解，得到满足优化目标的13个服务节点，其对应服务需求点及货运量如表2所示。

由表2可知，B1—B13各个服务节点对C1—C20各个需求点的货运量各不相同，除C3、C8、C10、C19外，其余需求点货物运输均来自于单一服务节点。以B1服务节点为例，B1总是针对局部相邻的C1、C2、C3需求点进行货物运输，因此，考虑路径优化及运输成本，每个物流需求点会尽可能从最近的服务节点获取物流。

表2 对应服务需求点及货运量Table 2 Service demand point and freight volume

由于地下物流系统网络节点由一级节点和二级节点构成，因此，根据节点货运量大小对求解得到的13个服务节点进行分级，其中一级节点4个，二级节点9个。具体分级结果如表3所示。

表3 服务节点分级情况Table 3 Classification of service nodes

汇总该地区物流园区、服务节点、物流需求点、物流园区与一级节点通道、一级节点与二级节点通道及节点服务区域，得到该地区地下物流系统网络节点及通道概况如图7所示。由图7可知，地下物流网络服务节点表现出明显的区域集中性，即服务节点均集中在物流需求点附近，且二级节点服务区域总是邻近某个一级节点。根据某一级节点的转运量为总出货量减去该物流园区间接与二级节点间的货运量之和，通过计算得到各一级节点转运率φ（见表4），平均转运率φ¯为64.27%。各节点转运率相对较为平均，地下物流系统网络有效降低并控制了节点转运率。