色纺纱计算机配色技术的研究现状及展望

崔翔宇 夏 鑫 杨月茹 张思雨 程 璐

（新疆大学，新疆乌鲁木齐，830046）

色纺纱是由多根已着色或具有天然彩色的散纤维，按一定比例混纺而成的纱线。它采用“先着色，后纺纱”的加工工艺，不仅免去了传统纺织中的染整工序，减少了污染，而且避免了染色时常出现的浸染、沾色等问题；在后整理时，色纺纱亦减少了纤维间因收缩或染整性能相异而形成的疵点［1］。多样的混纺工艺使得色纺织物的色彩丰富自然，色泽柔和含蓄，风格特异，色纺产品由此深受消费者喜爱，色纺工业的发展在近几年也相当迅速。

但色纺纱工业依然面临着很多亟需解决的问题与挑战，其一便是色纺纱计算机测配色的效率与颜色表达的准确度。本文拟从色纺纱的成色机理出发，综述并对比近年来诸学者在色纺纱计算机测配色方面的研究进展，对未来研究方向做出预测。

1 色纺纱成色机理

1.1 色纺纱显色原因

因异色纤维排列足够紧密，色纺纱交织所成的色点面积与视觉距离之比非常小，而人眼因分辨率的不足，将无法识别各单根有色纤维的色彩，感受到的是有色纤维混和体所呈现的一种新色彩。

这种以空间混合为主的成色机理，与加法混合、减法混合所不同的是，前者并非是色彩的真正混合，而是通过视觉距离与分辨率的关系达成。当人眼或其他感光元件距织物表面有一定距离时，即可呈现色纺织物的混色效果［2］，如图1所示。

图1 不同视觉距离下色纺织物的混色效果

1.2 色彩的空间混合

当各种颜色并置于一起，且它们的视网膜投影足够小时，这些不同的颜色刺激会同时作用到视网膜上非常邻近部位的感光细胞，以致眼睛很难将它们独立分辨，从而在视觉上产生色彩混合，这种混合称空间混合，又称并置混合［3］。

空间混合成色的效果取决于并置颜色排列的有序性、各颜色的对比度与互补关系、观察距离等3个方面。

色彩空间混合时，各部分依然保持原色，其混合产生新颜色RGB值可以用式（1）～式（3）表示。

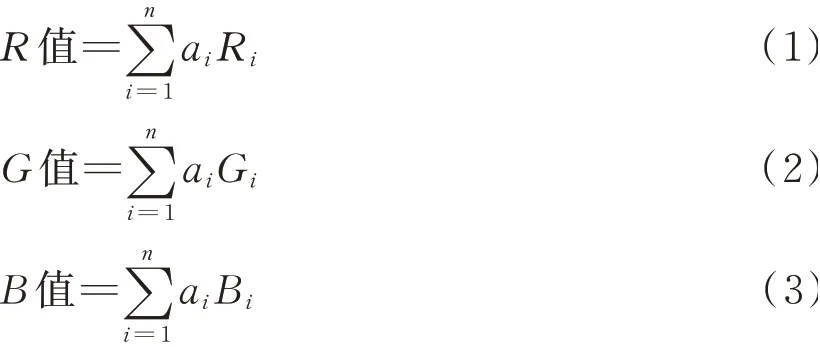
式中：ai表示混和颜色中第i组分所占百分比；Ri、Gi、Bi分别表示第i组单色样品的RGB值。

2 计算机配色算法

2.1 光谱匹配

反射光谱决定纺织品颜色，使产品的反射光谱与标准样品相匹配，不受光源和观察者的影响，可达到最完善配色，又称无条件匹配。其表达式见式（4），其中：P=WDΦ。

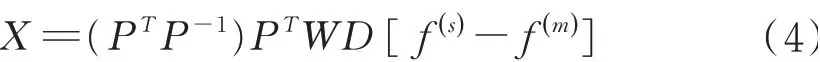
式中：X表示3种单色纤维分别的配比；W为31×31的方阵，其对角线是不同波长对应的权重因子，其余元素为0；D为31×31的方阵，其主对角线上排列标准样中各不同波长对应dλ值，其余元素为0；Φ在Stearns-Noechel模型与Friele模型中分别为关于标准样和真实打样的中间函数，为列矢量。

实际应用中，在400 nm～700 nm之间，每10 nm选取一个数据点以求得对应权重因子，罗列方程进行计算，最多可求出31种单色纤维的混色比。但光谱匹配很难使得实际打样与标准样的反射光谱完全匹配，故不断寻求更为接近的拟合样。

2.2 三刺激值匹配

三刺激值匹配拟通过真实打样与标准样的三刺激值进行比对相等，从而获得有效配方，其优势是不要求配色结果在反射光谱上与标准样相同。

应用了最小二乘法求解的三刺激值匹配可求解3种以内的单色纤维混色比［4］，对多色混色产品的生产有较强的制约性。同时，较光谱匹配的劣势是，三刺激值匹配过程对光源、观察者及仪器均有严格要求［5］，且易产生同色异谱现象。

但由于光谱配色的计算复杂及成本较高，在实际生产中难以达到经济且优良的拟合效果，故当下三刺激值匹配更普遍应用于生产。

3 计算机配色的理论模型

3.1 Kubelka-Munk理论

1939年，Kubelka与Munk基 于 完 整 辐 射 理论，提出Kubelka-Munk理论，建立了分光反射率与吸收系数、散射系数之间的函数关系。

在有色织物的计算机配色领域，简化处理得到式（5）。

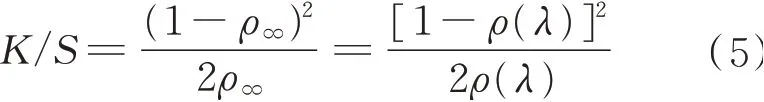
式中：ρ∞表示染色试样无限远时的反射率；K、S分别表示试样的吸收系数与散射系数。

该理论推导时建立的假设［6］：样品界面上折射率必须无变化；光线在介质内必须被足够地散射，以致呈完全扩散状态；光线在介质内的运动方向或所谓通道只考虑朝向相反（一个朝上，一个朝下）且垂直于界面的两个。

3.1.1 Kubelka-Munk单常数理论

纤维与染料对光的吸收系数K与散射系数S可加和，当染料已溶进纤维，即以分子形式存在且含量很小，故拟认为染料对纤维散射的影响是微不足道的，由此可将散射看作是由纺织纤维决定的，K/S值的计算推导见式（6）。

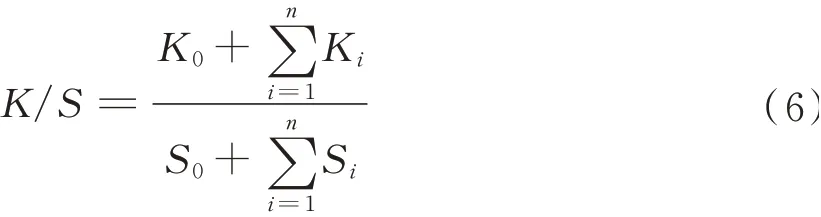
式中：K0、S0分别表示纤维的吸收系数与散射系数；Ki、Si分别表示各染料的吸收系数与散射系数。

Kubelka-Munk单常数理论被证明对基于减色混合的纺织品染色配方的预测效果较佳，但因色纺产品成色的特殊性，早期学者未取得满意的匹配结果，该方案也被认为不适用于色纺纱产品的测配色。

3.1.2 Kubelka-Munk双常数理论

有色纺织品的吸收与散射系数由各染料的吸收与散射系数共同决定，则配色时，K和S必须分别计算，见式（7）。

式中：（K/S）m表示混色试样的K/S值；ci表示第i种纤维占试样的质量比例；Ki、Si分别表示第i种纤维的吸收系数、散射系数。

以往的研究中，对混色织物中单色纤维的吸收系数K和散射系数S求解的常用方法为最小二乘法和相对值法。前者由WALOWIF E［7］最先提出，利用线性最小二乘回归算法，大大缩小K、S计算值与观测值间的差异；BURLONE D A［8］则通过假设一种纤维的相对K、S值，以计算混色织物的K/S值。

徐亚亚等［9-10］对数码转杯纱的混色纱进行研究，分别建立了利用以最小二乘法和相对值法求解的Kubelka-Munk双常数混色模型，并对比了两者对样本预测的色差。结果表明：对棉型纱，最小二乘法更适用于预测数码转杯纱的三原色混色效果及混色纤维比例；而针对毛型纱，则相对值法的预测精度更高。但两种方法并无显著优劣之分，并存在进一步提高精度的可能。

2019年，张婷婷等［11］对环锭数码纺混色纱测配色进行研究，采用相对值法求解参数，构建模型，并结合全光谱匹配和最小二乘法建立配色算法，平均色差控制在2以内。初步实现对环锭数码纺混色纱的颜色与配方预测。

3.2 Stearns-Noechel模型

1941年，DUNTLEY S Q［12］提出混色样品反射率是其组成各单色纤维反射率的质量加权和，见式（8）。

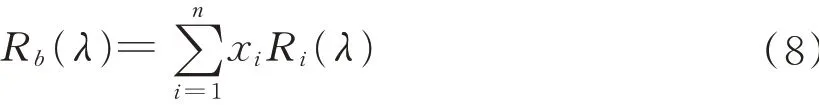
式中：Rb（λ）表示波长为λ时的混色样品反射率；xi表示第i组单色纤维在混色样品中所占质量分数，且满足表示波长为λ时第i组单色纤维的反射率；n表示混色样中的单色纤维数。

基 于Duntley的 理 论，Stearns与Noechel在1944年建立了Stearns-Noechel模型，修正了由于不同纤维间对光线散射和吸收的互相影响，以及单色反射率与其组成比例间的非线性关系等问题，并验证其对羊毛混色试样具有良好预测效果，见式（9）。

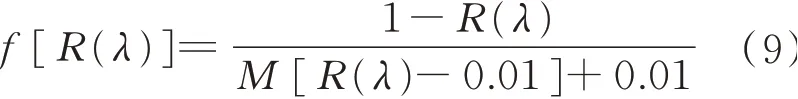
式中：M为可变常量，与混色样品中单色纤维的颜色、成分及织物组织结构有关；R（λ）表示波长为λ时，混色样品反射率Rb（λ）或单色纤维反射率Ri（λ）。

Stearns-Noechel模型是色纺纱计算机配色的代表性模型之一，它通过大量试验不断修正得出，其中最重要的环节是对可变常量M的确定。目前有较多学者基于该模型，对不同类型织物所对应M值进行研究。以下列举出诸学者研究得到的几种常规纤维所对应最优M值，见表1。

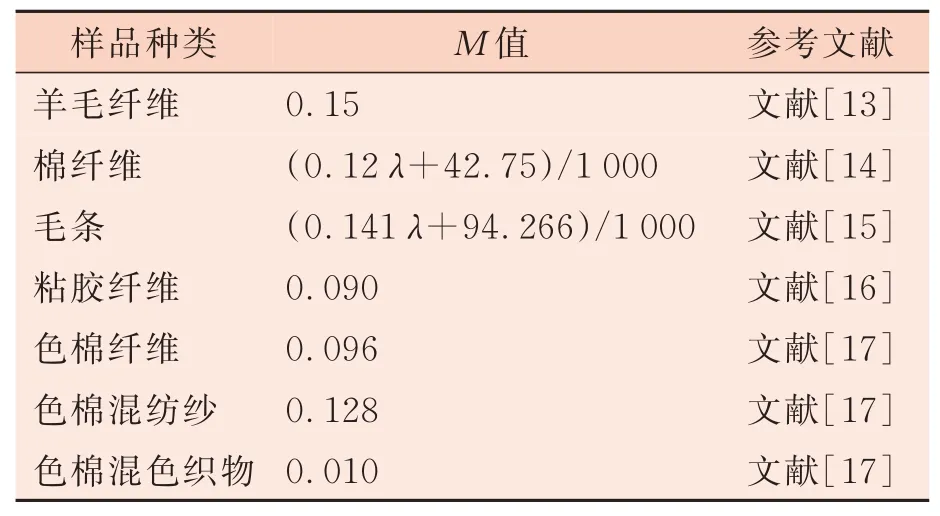
表1 纤维在Stearns-Noechel模型中的参数M值

在过往研究中发现，不同的纤维和织物组织结构，所对应M值不尽相同。针对不同纤维，需通过对大量试样的配色试验以优化参数。而生产中，因同种纤维的属性不同，或纺织工艺与机器设备等因素产生的色差是未知且难以控制的，修色的次数多和困难大直接影响到色纺产品的经济效益，且对于未公开最优M值的纤维，企业亦不便用作原料，故固定最优M值在实际生产的应用方面仍存在较大局限性。

王玉娟［18］基于Stearns-Noechel模型，建立了完整的计算机辅助色纺纱配色系统，在MATLAB环境中采用M值在［0，1］内赋值迭代的方法，赋予每个混色样不同的最优参数M值，避免大量前提试验，而且适用于任何种类纤维及单组份和多组分纤维混和。

2018年，白婧等［19］基于最优参数M值与反射光波长的关系，对Stearns-Noechel模型的参数确定做出优化，分别对非彩色与彩色色纺纱建立M值关于反射光波长的函数，并将配色结果代入CMC色差式验证，满足棉纤维配色要求。

2019年，马崇启等［20］以Stearns-Noechel模型为基础，采用赋值迭代法，比对最小色差来获得最优参数M值预测配方，并在此基础上将人眼视觉特性（假设人眼对于不同波长的反射率的敏感程度符合正态分布）用于色纺纱配色程序的优化，通过比较标准样与拟合样的色差大小判断配色效果，获得平均拟合色差为0.201，中位数为0.125，小于0.3，配色效果得到很大提高。

这种建立在拟定算法上，以赋值迭代参数M值寻找最优配色方案的方法，与传统方案中求固定值相比，更具灵活性与针对性，即依据实际打样进行针对性配色，减少打样和修色的复杂工作，且准确度较高，大大提高了配色效率，对企业生产中不同成分混色纱的实际配色更具可行性。

3.3 Friele模型

1952年，FRIELE L F C［21］基 于Duntley理论，根据有色介质对光线吸收和散射特性建立关于反射率R（λ）的函数，见式（10）。

式中：σ为可变常量；R（λ）表示波长为λ时纤维的反射率。

以下列举诸学者研究所得的几种常规纤维所对应的最优σ值，见表2。

表2 纤维在Friele模型中的参数σ值

沈加加等基于Friele模型的色纺纱计算机光谱配色原理，对大量试样求解，优化Friele模型参数σ值，并获得羊毛色纺纱参数σ值为0.093，棉色纺纱参数σ值为0.128。另外，作者由该试验指出：色差不是评估色纺纱配色准确性的唯一指标，色纺纱配色中还存在“同色异谱”问题，尚缺乏优良的解决方案。

2017年，马崇启等［26］利用MATLAB编写基于Friele模型的配色算法，对被测单色根据全光谱配色方案求拟合反射率，并在［0，1］范围内，每间隔0.000 1取σ值进行循环计算，对标准样和被测样的反射率进行比对，使得拟合色差小于1时输出结果。

Friele模型与Stearns-Noechel模型均是基于Duntley的混色质量加权和理论，通过对式中单一可变常量的确定与优化来匹配不同种类色纺纱的配色公式，但前者试验验证的纤维种类较少，且较于已有较大成果的Stearns-Noechel模型配色算法，Friele模型在面对相似的参数计算上，并未表现出显著的更简便易行或配色更精确等优势，故针对Stearns-Noechel模型的优化进展更具现实意义。

4 颜色评价与色差控制

4.1 颜色评价基础

色差是两试样在颜色知觉上包含明度差、彩度差、色相差的综合效应。在CIEXYZ颜色空间中，每种颜色对应互不相同的唯一点，曾有研究发现，在CIE7931x-y色度图的不同区域，人眼的分辨阈限不同，即人眼的颜色空间是不均匀的，色差也就不能简单用色点间的距离统一表示。以往学者常基于均匀颜色空间建立相应色差式，拟合了计算结果与视觉间的相关性。常见的色差式列举如下。

4.2 CIELAB色差式

4.2.1 CIE1976L*a*b*表色系统

CIE1976L*a*b*均匀色彩空间以孟塞尔表色系统为基础建立，与CIEXYZ颜色空间相比，可更好地依照人眼的色知觉属性拟合色差，该系统空间结构如图2所示。其中，L*为明度，C*为饱和度，h*为色相角。

图2 CIE1976L*a*b*表色系统示意图

X、Y、Z与L*、a*、b*间可以依据一定的函数关系进行转换。

4.2.2 CIELAB色差式

色差公式见式（11）。

式中：ΔL*表示明度差；ΔC*表示饱和度差；ΔH*表示色相差。

CIELAB色差式的精确度并不够好，但其色彩空间因查找颜色方便而被广泛运用。

4.3 CMC(l:c)色差式

以CIELAB色差式为基础，由于各影响因子在不同色彩区域内对总色差的贡献不同，则需根据色彩范围对ΔL*、ΔC*、ΔH*附相应系数加权求得总色差，其中，CMC（l：c）色差式是现今与视觉相关性较好且运用较为普遍的色差公式，见式（12）。

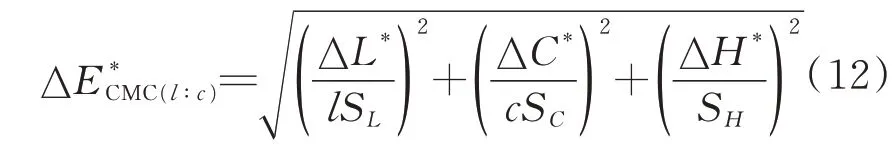
式中：SL、SC、SH分别表示明度差、色相差、彩度差的加权系数，均是与标准样色彩范围相关的函数；l、c分别表示调节明度差和彩度差的权重因 子，在 纺 织 行 业 中 取l∶c=2∶1，记 作CMC（2∶1）。

4.4 CIE2000色差式

在与CMC（l：c）色差式相似的CIE94色差式的基础上修正的CIE2000色差公式，改善了对中性色和蓝色区域的预测性能，校正了彩度差与色相差的交互项。其色差评估参数ΔE*00较CIELAB色差式中的评估参数而言，是一个主轴在饱和度方向与人眼辨别临近区更接近的椭圆［27］，其公式见式（13）。

式中：KL、KC、KH分别表示调节明度差、饱和度差、色相差的权重因子；RT表示旋转系数；在纺织行业中通常取KL=2、KC=1、KH=1。

尽管CIE2000色差式被视为现今最符合人视觉感官的，但其色彩空间依然不是完全均匀的，而在非直接测色获得颜色值的情况下，运行CIE2000色差式的处理耗时要显著高于CIE94等［28］。故而，当生产需求偏重于效率时，CIE2000并不一定是最优选择。

CMC（l：c）色差式与CIE2000色差式在对大量试样目测结果分析归纳的方法不同，导致了其加权系数确定的不同。在一些试验过程中，利用以上两种公式计算得到的拟合色差不尽相同，无法判断何者更接近真实色差。但对现有色差公式的改进研究仍具有现实意义。

4.5 反射率偏差评价颜色

视网膜皮层理论指出，视觉颜色与表面的光谱反射率函数有密切的关系，而与投射到视网膜上的光谱特性关系不大［29］。基于物体反射率评价织物颜色，可避免由光照和几何条件对测色产生的误差。

对色纺纱配色准确性的评估中，亦有学者采用反射率偏差值代替色差作为选择标准，以确定配方。

2018年，程璐［30］基于Stearns-Noechel模型，将最优M值的选择标准由色差最小改为拟合样与标准样的偏差值最小，在保证与标准样色差小于1的前提下，配色精度和拟合度得到提高。

2019年，朱宝基［31］同样采用反射率偏差值作最优参数选择标准，优化了基于Friele模型的配色算法，同时评价标准由色差改为配方相对偏差。

值得一提的是，在以上研究中均出现了以色差为标准选择的配方与以反射率偏差为标准选择的配方间存在较大差异的现象，而该问题尚未得到合理的解释。

4.6 对色差控制的其他研究

2019年，张靖晶［32］针对计算机配色的基础问题进行研究，分析了三刺激值计算的误差原因，分别针对测量间隔和带宽，测量范围进行优化，所采用的Table LWL算法使测量误差减小到未经处理的0.8%，范围不足时利用外延方法显著降低截断误差，提高了测算精度。

同年，朱宝基对纤维结合体色彩的影响因素做出研究分析，发现不同纺纱工序导致色差的出现，并发现其色度学参数变化呈一定规律性，从而对试样的色差进行初步预测。同时提出，规范纱线和织物的测色标准，是减少误差的重要方式。

5 现存问题及发展方向的预测

（1）现有对色纺纱成色机理的研究仍有待改进，可尝试进一步探究其空间混合的成色机理，对不同纤维、不同表面结构的织物进行试验验证，并将其在配色模型及算法的改进上合理运用，可对现有计算机配色方案的改进有所帮助。

（2）三刺激值匹配算法在应用中出现的“同色异谱”现象仍缺乏有效解决方案，光谱匹配算法的准确性有待进一步提高，对计算量的简化和测色成本的降低也存在实际研究意义。

（3）基于Kubelka-Munk双常数模型的拟合配方尚有缺陷，可尝试进一步优化对参数的计算，减小色差；针对Stearns-Noechel模型或Friele模型，应依据实际生产的条件及需要，优化对参数赋值迭代的方法改进配色方案，并对多种纤维进行试验，验证其通用性。

（4）现有色差公式与人眼建立的相关性并不强，且对观测条件具有严格要求；基于人眼大数据建立更详细、更准确的对比关系，将更有利于行业优选出适合的公式；实际打样与不同色差公式计算的标准样拟合色差不同，尚没有确切依据证明哪种结果更接近真实色差。

（5）色差并非评估色纺纱配色准确性的唯一标准，以反射率偏差为选择标准的算法仍有待进一步研究；对试验中出现的色差最小的拟合配方与真实反射率偏差最小的拟合配方不一致现象可成为色纺纱计算机配色的重要研究方向。