数显倾角仪校准方法

/ 潍柴动力股份有限公司

0 引言

随着技术发展，小型数显倾角仪开始出现，取代了笨重、携带不便的框式及条式水平仪，由于数显倾角仪小巧，方便携带，且带有磁条，广泛用于机械工作台、车床及切削工作台的水平位置检测，建筑工程设备的倾斜角检测及铁道系统铁轨水平度的检测等等，尤其适合倾斜角度大的检测设备。不用手扶，减少了人为影响因素，自由吸附在被测量面，方便高效测量，且测量范围远远大于传统水平仪。

随之引入的是如何实现数显倾角仪的校准，查阅了相关文献，未找到相关的国家规程和行业标准。本文结合数显倾角仪的特点，借助量块和正弦规实现了数显倾角仪的校准。

1 数显倾角仪的结构及校准参数

查阅了数显倾角仪（图1）的产品说明书[1]，测量范围介于0°～90°，最大允许误差不大于±0.2°，分辨力0.05°，重复性不大于0.1°。根据其工作原理及出厂参数，将最大允许误差及重复性这两个参数纳入研究范围。

图1 数显倾角仪

根据数显倾角仪的测量范围和使用范围，将校准点分布在：0°、30°、60°、90°4个点，因45°为其使用角度，增加45°校准点。

1.1 示值误差校准

将正弦规放置于平板上，将数显倾角仪吸附在正弦规工作面上（图2），调整数显倾角仪示值于零位，然后依次在正弦规的圆柱下面放置相应校准点所需尺寸的五等量块，并在数显倾角仪上逐个读取示值。示值误差的校准应在正、反两行程方向上进行。各校准点数显倾角仪示值与相应正弦规产生的角度值之差为各校准点的示值误差。校准完一侧示值误差后，将数显倾角仪调转180°方位，用相同的方法校准另一侧测量范围的示值误差。最终取各个校准点示值误差最大值的绝对值作为数显倾角仪的示值误差。

图2 数显倾角仪校准示意图

所用量块的组合尺寸H的计算公式如式（1）：

式中：H—— 量块的组合尺寸，mm；

L—— 正弦规两圆柱轴线间距，mm；

α—— 各校准点角度值，（°）

根据所用的正弦规（L= 200 mm）分别计算出被校准点的量块组合尺寸，并确定量块的选配方案。

如30°校准点，所用量块组合尺寸H= 100 mm，则其选配量块的组合参考方案为：（100 mm长度最大极限偏差为±2.5 μm，换算成角值偏差修正量为+2.98″）；45°校准点所用量块组合尺寸为H= 141.42 mm[选配量块组合参考方案一：100 mm +40 mm+1.42 mm，长度最大极限偏差为 ±（2.5 + 1.6+ 1） μm=±5.1 μm，换算成角值偏差为 5.46″]，同样的，其他校准点依次按照式（1）进行量块尺寸计算。

1.2 重复性校准

将正弦规放置在平板上构成一个水平倾角，用数显倾角仪对该倾角进行7 次重复测量，其最大差值的绝对值为重复性。

选择45°校准点，借鉴JJG 103-2005《电子水平仪和合像水平仪》检定规程[2]进行重复测量，其中最大差值的绝对值不超过0.1°，见式（2）：

式中：δ—— 重复性，（°）；

αmax—— 7 次测量示值中的最大值，（°）；

αmin—— 7次测量示值中的最小值，（°）

2 不确定度评定

以45°校准点为例，评价正弦规对数显倾角仪校准的测量不确定度。

2.1 测量模型

式中：Δα—— 数显倾角仪示值误差，（°）；

αi—— 数显倾角仪的显示角度值，（°）；

α—— 正弦规与量块产生的角度值，（°）

2.2 不确定度来源

1）角度测量重复性引入的不确定度u(α1)；

2）正弦规两圆柱轴线间距误差引入的不确定度u(α2)；

3）量块示值误差引入的不确定度u(α3)；

4）平板平面度误差引入的不确定度u(α4)；

2.3 输入量的标准不确定度评定

2.3.1 角度重复性引起的不确定度u（a1）的评定，采用A类方法进行评定。

对数显倾角仪连续测量10次，得到测量列45.20°、45.10°、45.10°、45.15°、45.15°、45.10°、45.15°、45.20°、45.20°、45.15°。

则可得到

u(a1) =s= 93.6″

2.3.2 正弦规两圆柱轴线间距误差引入的不确定度u(α2)的评定，采用B类方法进行评定。

查阅JJG 37-2005《正弦规》检定规程[3]两圆柱中心距的偏差要求±1 μm，换算成角值为1.03"，统计分析该分量接近均匀分布，包含因子为，则

2.3.3 量块示值误差引入的不确定度u(α3)的评定，采用B类方法进行评定。

查阅 JJG 146-2011《量块》检定规程[4]规定，100 mm 量块长度最大极限偏差为 ±2.5 μm，40 mm量块长度最大极限偏差为±1.6 μm，1.42 mm量块长度最大极限偏差为±1.0 μm，总最大极限偏差为±5.1 μm，换算成角值偏差为5.46″，统计分析该分量接近均匀分布，包含因子为，则

2.3.3 平板平面度误差引入的不确定度u(α4)的评定，采用B类方法进行评定。

查阅JJG 117-2013《平板》检定规程[5]规定，0级平板任意250 mm×250 mm局部工作面的平面度允许限为3.5 μm，换算成角值偏差为4.17″，统计分析该分量接近均匀分布，包含因子为，则

2.4 合成标准不确定度及扩展不确定度

2.4.1 灵敏系数

2.4.2 不确定度分量汇总

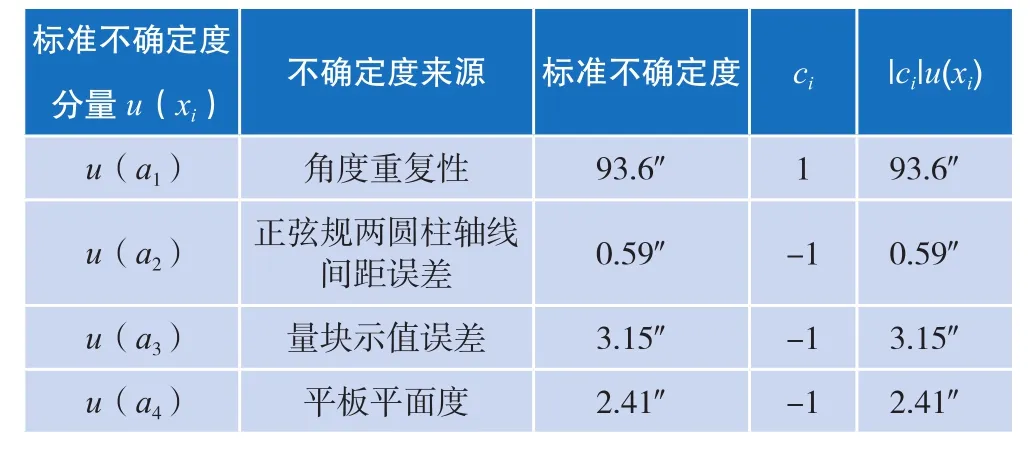
表2 标准不确定度汇总表

2.4.3 合成标准不确定度的计算

输入量Li、L0及Ls彼此不相关，所以合成标准不确定度可按下式得到：

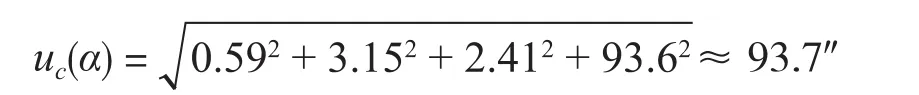
2.4.4 扩展不确定度的评定

取k= 2，扩展不确定度为：

U= 2uc（α）= 2×93.7 ≈188'' = 0.052°＜MPE/3 =0.067°

2.4.5 由测量不确定度的构成来看，其主要影响分量为角度重复性引入，按照同样的方法，对0～90°测量范围内的其他角度进行不确定度评定，重复性都在0.1°范围内，计算得到：

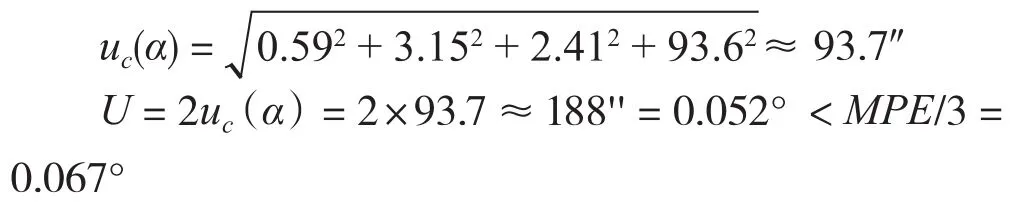
从测量不确定度来看，此方法满足数显倾角仪的量传要求。

3 结语

通过以上分析，采用正弦规和量块对数显倾角仪进行校准，无论从操作可行性还是量传准确性方面都满足要求，校准方法可行，可以正常量传。