中学地理三角形坐标图深度教学初探
2020-11-13福建沈志强
福建 沈志强
以“素养立意”建构课堂,基于“深度探究”走进“深度教学”才是基于核心素养的教学。本文以变式三角形坐标图诱发高阶思维问题,深入探究,归纳三角形坐标图的判读方法,证明三角形坐标图的统计原理,推导变式三角形坐标图的通用模式,运用由表及里的深度教学,能够改善学生的思维结构,培养学生独立思考能力和创造性思维能力,提升学生对复杂问题的探究能力和解决能力。
一、话说三角形坐标图
三角形坐标图,外围是一个正三角形,三边坐标轴一般按逆时针方向标注由0到100%递增的变量值,在三角形内部做出三边的若干条平行线。三角形坐标图的点表达了三项地理要素的相对百分数(%),揭示了某一地理事象的局部与全部的数量比例关系。三角形坐标图以有限的平面空间,在理论上却能无限地承载无数个地理事象,以其外形简洁、载点多的优势在统计图中占有一席之地,也能很好地训练或考查学生的地理统计能力及其分析应用能力。
二、借助试题情景,激发问题意识
核心素养的教学应立足于现实生活中的真实素材,课上借用复杂的问题情景,诱发问题意识,让学生通过读取有效的试题信息,并与学科内外的基础知识和原理规律进行对接,重组融合和迁移应用,运用已有的多学科知识和技能去探究实际问题,解决实际问题,并形成新的知识和技能。借助于复杂问题情境,激发学生的问题意识,由“深度探究”走进“深度教学”是培养学生地理核心素养的一个关键环节。为此在学习一般三角形坐标图之后,笔者特地引入如下的变式三角形坐标图试题。
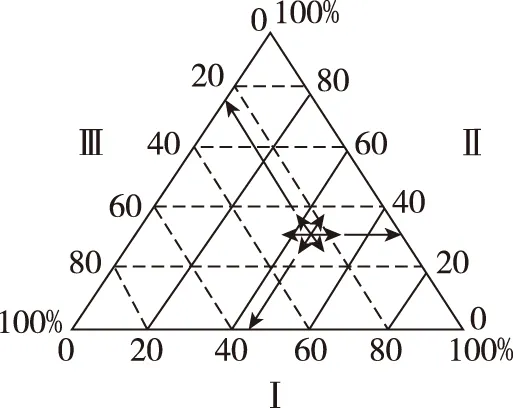
【试题呈现】下图示意我国1985—2005年不同地区劳动密集型制造业市场份额(%)变化情况,读图完成1,2题。

1.Ⅰ区劳动密集型制造业向外迁移的趋势,始于
( )
A.1985年 B.1995年
C.2000年 D.2005年
2.导致Ⅲ区劳动密集型制造业市场份额变化的原因,不可能是
( )
A.西部大开发的推进
B.国内外的产业转移
C.产品质量的提升
D.当地政府的支持
【试题分析】从三角形坐标图看,三轴百分数也并非一致性的由0到100%递增,但通过抽检会发现(如1995年Ⅰ,Ⅱ,Ⅲ区的对应相对数为50%、40%、10%,三个市场份额总和为100%)这是一个新颖的变式三角形坐标图。
由图判读可知Ⅰ区1985、1995、2000、2005年的市场份额依次是40%、50%、55%、50%,呈现先剧增(2000年之前)、后略减(2000年之后)的变化,也说明从2000年开始Ⅰ区企业有外迁之势,故1题选C。再判读出Ⅲ区1985、1995、2000、2005年的市场份额依次是10%、10%、13%、20%,呈现“持平—略增—剧增”的变化,随着西部大开发,位于我国东部的Ⅲ区更有可能是劳动密集型企业大量被转移到西部,Ⅲ区劳动密集型企业的增加趋势成为不可能,故2题选A。
【问题提升】学生思维活动始于问题,问题意识应是深度教学之始,问题教学也应该贯穿于深度教学的整个过程中,更让问题教学成为深度教学的一种常态。我们也在上述试题探究之余,产生以下若干问题,并由此延伸三角形坐标图的深度教学。
1.三角坐标图的判读有哪几种?对于三角形坐标变式图的判读用哪种方法会更好?
2.在三角形坐标图中,为什么某点的百分数之和是100%?
3.变式三角形坐标图三轴百分数并非一致性的从0~100%,那么,它又该是一种怎样的数据模式?与一般三角形坐标图又有何关联?
以上“高阶思维”的问题,无疑会成为我们后续探究的助推器,更是课上培养学生的理性思考和创新能力的催化剂。
三、整合学科知识,施行深度教学
整合学科知识既符合新课改精神,也符合探究性课程的设计要求。它不仅体现学科内系统知识的整合,也尽可能体现其他学科服务于学生发展的功能。开展整合性的跨学科主题教学,是深度教学的核心环节,是培养学生综合思维、知识迁移能力、解决复杂问题能力的重要途径。继上述试题探究之后,可以尝试如下关于三角形坐标图的主题式教学。
1.归纳三角形坐标图的判读方法
(1)平行(小值)斜轴法
先是立足坐标图外侧,逐一面对Ⅰ,Ⅱ,Ⅲ三横轴,每一横轴的两端为0和100%,其中把过横轴端点0(数值较小)的斜轴称为“小值斜轴”。然后过图中的某点向每一横轴逐一作其“小值斜轴”的平行线(见下图),并交于Ⅰ,Ⅱ,Ⅲ轴上三点。最后读取Ⅰ,Ⅱ,Ⅲ轴上三点的百分数(30%,23%,47%)。

(2)平行(增大)箭头法
首先在三角形坐标图Ⅰ,Ⅱ,Ⅲ轴外侧作三个“增大箭头”(见下图),即箭头指向与变量轴百分数的增大方向一致。再过图中某点分别向Ⅰ,Ⅱ,Ⅲ轴作与外围“增大箭头”的平行的箭头,且让“平行箭头”延伸至变量轴。最后读取Ⅰ,Ⅱ,Ⅲ轴上的箭头读数(28%,44%,28%)。

(3)延伸(小值)箭头法
首先过三角形坐标图中的某点,作平行于三个横轴3对两两反向的6个辐射小箭头(见下图)。然后立足于每一横轴,恰有两个小箭头扑面而来,并对数值较小的辐射小箭头加以延伸。最后逐一读取延伸箭头在Ⅰ,Ⅱ,Ⅲ轴上的百分数(45%,30%,25%)。
值得注意的是,无论用哪种方法获取的读数,最后都必须进行“验证”环节,即累加三轴的读数之和是否为100%,再进行“校正”读数,避免或减少读数误差。
上述三种判读方法,不仅适用于一般三角形坐标图,也适用于变式三角形坐标图,还适用于三轴百分数呈顺时针方向增大的三角形坐标图。
比较三种判读,平行箭头法和延伸箭头法判读步骤清晰,初学者容易掌握。不过,也因画上的辅助箭头等符号较多,多少会给原图“添乱”。平行斜轴法判读步骤清晰,也无须画上繁多的辅助线条和符号,尤其是对于某一地理要素在单一横轴上的读数和比较,平行斜轴法更显简明而快捷(如上述试题),更为许多学者所赏识和运用。但也因受熟悉的直角坐标图判读思维的干扰,初学者也许会觉得不太习惯。
2.证明三角形坐标图的统计原理
假设:在下图中有一点P,过P点分别向三横轴AB、BC、CA作各自“小值斜轴”平行线PX,PY,PZ,并分别交于横轴上的X,Y,Z三点,设AX=x,BY=y,CZ=z.
求证:首先,过Y点向AB横轴再作“小值斜轴”的平行线YD,交横轴于点D.
XD=PY(平行四边形对边相等);PY=CZ=z(等腰梯形腰长相等);所以XD=z.
DB=BY=y(正三角形边长相等).
因为横轴AB=AX+XD+DB=100%,
所以AB=x+z+y=100%(等量代换).
结论:P点在三横轴的读数之和x+y+z=100%.

3.推导变式三角形坐标图的通用模式
在上述试题中,变式三角形坐标图图式新颖,可读性强,很能激发学生的探究欲望。通过探究,也利于培养学生“透过现象看本质”的洞察能力和“以不变应万变”的应用能力。经过对变式三角形坐标图的深入思考与细致推敲,可得变式三角形坐标图的通用模式,具体推导过程如下:
假设:在下图变式三角形坐标图中,设三等轴长为l(0 求证:P点在三轴读数之和X+Y+Z =(x+l1)+(y+l2)+(z+l3) =x+y+z+l1+l2+l3 =x+y+z+l(图6中l1+l2+l3为AB轴长l) 即x+y+z+l=100%(三角形坐标图统计原理P点在三轴读数之和为100%). 结论:变式三角形坐标图的通用模式即x+y+z+l=100%(0 例如上述试题中的变式三角坐标图(见试题1),三轴起点百分数0、20%、40%和轴长百分数40%之和为100%。 其实,一般三角形坐标图只是变式三角形坐标图的一种特例,变式三角形坐标图的通用模式也是适用的。因而,对于变式三角形坐标图的通用模式x+y+z+l=100%(且0 以上深度教学,其内容涵盖了三角形坐标图的判读方法、统计原理、通用模式等地理统计知识的整合,也涉及数学统计、几何证明等数学方法的运用,还涉及特殊性与普遍性等政治原理的应用。借助试题,高阶思维能很好地触及学科的本质和知识的内核,主题式探究也能促进学生的深层学习与能力发展的内部转换,深度教学具有一定成效。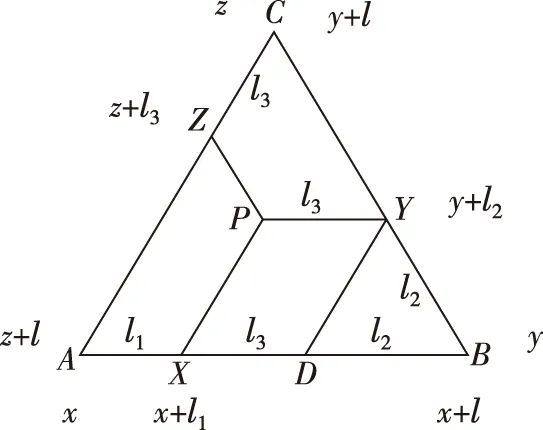
四、教学感悟

