“高层住宅采光”考向分析及教学启示
2020-11-13广西侯刘起
广西 侯刘起 李 帅
“高层住宅采光”问题是正午太阳高度及其变化等地球运动知识在生活中的应用,是高考考查的重点内容。本文从课程标准、内容、试题等角度分析高层住宅采光的考向,并从中得出教学启示。
一、课标分析
《高中地理课程标准(2017版)》要求“结合实例,说明地球运动的地理意义”。课标中的行为动词是“说明”,这个词语对应很高的核心素养,要求我们能够对地理事象进行剖析,对地理原理、规律进行解释。在学习方式方面,课标要求“结合实例”“从具体的地理事物和现象出发,分析现实问题”;在学习结果方面,课标要求“形成系统、全面、动态地分析地理问题的方法”。
二、内容分析
“高层住宅采光”是生活实例,是正午太阳高度及其变化等地球运动知识在生活中的应用。《中华人民共和国国家标准城市居住区规划设计规范》规定“冬至日日照时间不少于1小时”。因此,借助高层住宅采光这一实例可以“从具体的地理事物和现象出发,分析现实问题”,进而达到“结合实例,说明地球运动的地理意义”的目的。
住宅的光照主要来自太阳辐射,因此,高层住宅采光主要考查太阳直射点的回归运动、正午太阳高度及其变化、正午太阳高度与影长的关系、影长与楼房遮挡的关系等知识。
三、典例展示
(一)正午太阳高度与影长
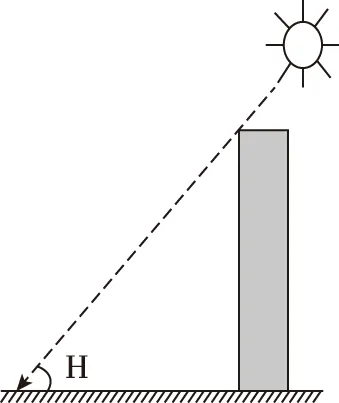
【例1】下图示意我国某地的一幢楼,冬至日正午该楼的影长与楼高相等,该地的纬度是
( )
A.23°26′N B.21°34′N
C.25°26′N D.23°34′N
【解析】该题以我国某地一幢楼影长与楼高的关系为背景,考查正午太阳高度与影长的关系、正午太阳高度角的计算等知识。因为正午该楼的影长与楼高相等,所以此地冬至日的正午太阳高度为45°。冬至日时太阳直射23°26′S,根据正午太阳高度角的计算公式H=90°-|Φ-δ|(Φ为当地纬度;δ为太阳直射点的纬度)可知,H=90°-|Φ-(-23°26′)|。经计算可知当地纬度Φ为21°34′N,B选项正确。
(二)影长与楼房遮挡
【例2】11月22日,某地理研究性学习小组在观测房屋采光状况时,发现甲楼阴影恰好遮住乙楼三层中部(如下图所示),在甲楼顶层GPS测得纬度为31.836 6°N、经度为117.217 9°E、高程为96 m。

隔25小时再次观测时,甲楼的阴影可遮挡乙楼
( )
A.二层西部 B.四层东部
C.五层西部 D.七层东部
【解析】该题以某地理研究性学习小组对房屋采光状况的观测为背景,考查太阳直射点的移动与正午太阳高度的变化、正午太阳高度与影长的关系、影长与楼房遮挡的关系、光照方向与物影方向的关系等知识。该地的纬度为31.836 6°N,位于北回归线以北地区,11月22日太阳直射点位于南半球且向南移动,因此,未来一段时间内该地的正午太阳高度逐渐变小,影长逐渐变长。从材料及图中可知,此时为正午且阴影正好到三楼顶部,隔25小时再次观测时,该地影长变长且处于下午。影长越长,可以遮挡的楼层越高,因此甲楼的阴影可遮挡到乙楼的四层。下午太阳光来自西边,物影位于东边,因此,隔25小时再次观测时,甲楼的阴影可遮挡乙楼的四层东部,B选项正确。
【例3】近年来,我国房地产业发展迅速,越来越多的居民乔迁新居,居住条件和环境显著改善。请读下图,运用以下公式及相关知识回答问题。

①H=90°-|Φ-δ|公式中H为正午太阳高度;Φ为当地纬度,取正值;δ为太阳直射点的纬度,当地夏半年取正值,冬半年取负值。
②tan35°≈0.7 tan45°=1 tan60°≈1.732
房地产开发商在某城市(30°N)建造了两幢商品住宅楼(上图),某户居民买到了北楼一层的一套房子,于春节前住进去后发现正午前后太阳光线被南楼挡住。请问,该房子一年中正午太阳光线被南楼挡住的时间大约是
( )
A.1个月 B.3个月 C.6个月 D.9个月
【解析】该题以某城市的两幢商品住宅楼为背景,考查太阳直射点的移动、正午太阳高度角的计算等知识。从图中可知,南楼与楼间距的比值为69 m/40 m=1.725,即南楼与楼间距比值所成角的正切值为1.725。因为tan60°≈1.732,所以南楼与楼间距比值所成的角约等于60°。根据正午太阳高度与影长的关系可知,正午太阳高度角越小,影长越长。根据影长与楼房遮挡的关系可知,影长越长,楼房越容易被遮挡。因此,当正午太阳高度角H≤60°时,南楼就会遮挡北楼。该城市的纬度为30°N,所以春秋分的正午太阳高度H=90°-|30°-0°|=60°。根据正午太阳高度的季节变化规律可知,该城市的正午太阳高度角夏半年大于60°,冬半年小于60°。因此,该房子一年中正午太阳光线被南楼挡住的时间大约是6个月,C选项正确。
(三)楼房遮挡与对策
【例4】阅读材料,完成下列各题。
材料一下图为南京市(约32°N)某两栋居民楼示意图。
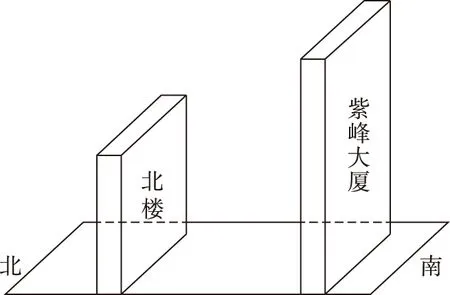
材料二据报道:南京高楼“紫峰大厦”建成后,居住在北楼南侧的陈先生发现居室日照时间变短,不足1小时。依据我国相关法规的规定,一年中,住宅建筑白昼最短日的日照时间应满足大于或等于1小时的标准。
为使已建北楼住宅的日照达到法规要求,假设在北楼南方重新规划建设紫峰大厦,请你简单说出两种合理的设计方案。
【解析】该题以南京高楼“紫峰大厦”的建设为背景,考查楼房遮挡与对策等知识。根据楼房遮挡与影长的关系可知,当影长小于楼间距时,则楼房不会被遮挡,而影长又和正午太阳高度角、南楼(紫峰大厦)的高度有关系。因此,可以从南北楼的间距、南楼的高度等方面提出合理的设计方案。
【答案】保持紫峰大厦的高度,加大两楼的间距以达到要求;保持两楼间距,降低紫峰大厦的设计高度以达到要求。
四、教学启示
结合对课程标准、内容、试题等的分析,提出“高层住宅采光”的考向,并从中得到以下教学启示。
(一)在复习旧知中构建知识体系
在解答“高层住宅采光”相关试题时,需要学生在复习旧知识中构建知识体系,特别是要牢牢掌握正午太阳高度的计算、太阳直射点的回归运动、正午太阳高度的变化、正切函数的概念及性质等知识。比如,例1需要利用正切函数的概念、正午太阳高度的计算等知识;例2需要利用太阳直射点的回归运动、正午太阳高度变化等知识。
(二)在理清关系中明确分析思路
“高层住宅采光”相关试题中的地理要素比较复杂,因此,在解答“高层住宅采光”相关试题时,需要学生理清各种关系。比如例1需要学生理清影长与楼高的关系;例2需要学生理清太阳直射点移动与影长的变化关系、影长与楼房遮挡的关系、光照方向与物影方向的关系。
(三)在梳理方法中突破学习难点
“高层住宅采光”对数学计算方法的要求较高。比如正午太阳高度角的计算中隐含了绝对值函数的思想;楼高与楼间距的比值蕴含了正切函数的概念及其性质。因此,在解答相关试题时,需要学生梳理相应的计算方法。比如例1和例3需要学生梳理正午太阳高度的计算公式;例1需要学生梳理正切函数的概念;例3需要学生梳理正切函数的性质。
(四)在关注生活中提升应用能力

