浅析迁移策略 提升物理核心素养

浙江 方道余

一、迁移及其在学习中的意义

新修订的《高中物理课程标准》，将物理课程目标中的具体目标(三维目标)深化为“物理核心素养”。物理核心素养是学生在接受物理教育过程中逐步形成的适应个人终身发展和社会发展需要的必备品格和关键能力，是学生通过物理学习内化的带有物理学科特性的品质，是学生科学素养的关键成分。发展核心素养可简单地理解为：学生通过学习，能够把所学知识、培养的能力应用到新环境、新情景中去。而学会知识间的迁移有两种，一种是将处于同一层次，在难度和复杂程度上大致属于同一水平的知识进行迁移，使彼此之间存在某种联系，这种迁移称为水平迁移或横向迁移，如学习了抛体运动知识后，可将其迁移到带电粒子在匀强电场中运动的学习；另一种是把非同一层次，难度和复杂程度上均不在同一水平面的知识之间进行迁移，这种迁移称为垂直迁移或纵向迁移，如电流的磁效应和电磁感应的学习有助于电磁波知识中电磁波的产生和传播的学习。

也就是说，学习的最终目的，并不是将知识经验储存于头脑中，而是迁移到各种不同的问题情景中，解决各种实际问题。因此在物理习题教学中，要指导学生利用迁移策略来解决并强化物理问题，培养学生将已有知识与新情境新事物相联系的能力。

二、物理习题教学中的迁移策略

1.水平迁移策略

由于并列结合的物理问题与已有的某“知识组块”之间存在状态或过程的相似或相同要素，因此可用水平迁移的方法解决这类问题。习题教学中要引导学生进行相似的物理状态或过程分析，寻找出相同要素，从而顺利实现水平迁移，使知识类化。用心理学的观点看，这是一个知识同化的过程。

【母题】如图1所示，在一竖直面内有一光滑的轨道，轨道左边是光滑弧线，右边是足够长的水平直线。现有质量分别为mA和mB的两个质点，B在水平轨道上静止，A在高h处自静止滑下，与B发生弹性碰撞，碰后A仍可返回到弧线的某一高度上，并再度滑下。问：A、B的质量满足什么关系时至少可以发生两次碰撞。

图1

【解析】A与B间的碰撞是一个弹性碰撞过程，它是所有碰撞过程中一种极端的情况即形变能够完全恢复，机械能没有损失。弹性碰撞除了遵从上述的动量守恒定律外，还具备碰前、碰后系统的总动能相等的特征。设A球与B球第一次碰撞前速度为v0，碰撞后A球和B球的速度分别为vA和vB。A球从轨道上下滑的过程，由机械能守恒定律得

对于A、B碰撞的过程，取向右为正方向，根据动量守恒定律和能量守恒定律得

mAv0=mAvA+mBvB

要使A、B两球至少发生两次碰撞，第一次碰撞后A球反向弹回，且A球的速度大小必须大于B球的速度，则

vA<0，|vA|>vB

联立解得mB>3mA

【点评】这道题利用了弹性碰撞过程遵从动量守恒定律和碰前、碰后系统的总动能相等的特征，再结合A、B能进行第二次碰撞可得出：第一次碰撞后A球反向弹回，经左边的光滑弧线后反向向右运动的速度大小必须大于B球的速度，这样才能实现至少两次碰撞，由此列式子结合条件得出结论。

【变式一】如图2所示，有一质量为mB的光滑小车静止在光滑的水平面上，其右端与平台相切，一个质量为mA的小球以速度v0滑上小车后又返回下来，当小球离开小车时，mA和mB的速度各是多少？

图2

【解析】通过该问题与上面的母题弹性碰撞的过程相似性分析，遵循动量、机械能转化的相似性分析，可知小球和小车相当于经历了一次弹性碰撞。因此可将弹性碰撞的有关知识和规律直接迁移过来，则

mAv0=mAvA+mBvB

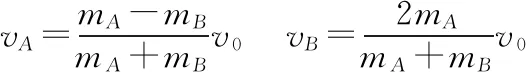
【点评】变式一与上面的母题对比，这道题依然涉及两个物体运动，只是带有光滑弧面的小车代替了母题中的小球B。对此，学生不容易判断动量是否守恒。我们可以引导学生根据动量守恒条件分析，在竖直方向上小球动量发生变化，而小车动量不变。判断出小球与小车组成的系统动量不守恒，进一步引导学生类比母题思考，在水平方向上系统动量是否守恒，从而应用动量守恒。最后迁移母题的思路，由此根据水平方向动量守恒与机械能守恒，综合求解。

【归结】要使水平迁移顺利完成，在平时物理习题教学过程中要经常采用“一题多变”的教学模式，指导学生对有关问题进行归纳整理，使知识类化；同时也要经常采用“题组”教学法，引导学生应用水平迁移策略的复习。如：

①如图3所示，甲、乙两图分别表示在光滑的水平面上，木块被子弹击中和一滑块m滑上质量为M的小车，实际上也是同一个问题，不同点在于作用快慢不一样。

甲

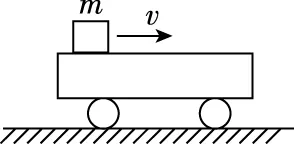
乙

②如图4所示，在甲、乙、丙中，一切表面光滑，如果m从右端运动到左端，比较一下有哪些相同要素呢？

甲

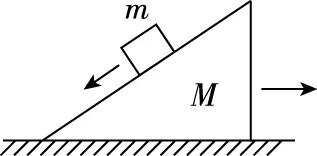
乙

丙

这样的训练，有助培养学生对迁移认知思想的理解。从教学实践可知，学生对水平迁移的认知能力越强，迁移的跨度就会越大，迁移就越容易实现。

2.垂直迁移策略

物理综合题符合垂直迁移策略的应用，其包括多过程问题、多体问题和跨学科(物理分支学科)问题。要顺利解决这类物理问题，学生必须具备较强的分析分解能力，从而准确、快速地将这类综合问题分解成小的知识模块，然后利用已有的“知识组块”解决每一个小问题，实现垂直迁移完成解答。用心理学的观点看，这也是知识同化的过程。

【变式二】如图5所示，一轻质弹簧两端连着质量分别为mA=0.09 kg，mB=0.1 kg的两木块A和B，放在光滑的水平面上，如果物块A被水平速度为v0=800 m/s，质量mC=0.01 kg的子弹C射中并嵌在物块A的中心，求弹簧的最大弹性势能。

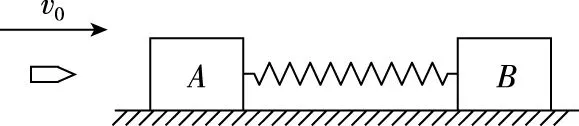
图5

【解析】与上面的母题对比，这道题涉及的运动物体有木块A、木块B、子弹C以及轻质弹簧；可以分两个过程，过程一为子弹C打入木块A；过程二为子弹C和木块A一起压缩弹簧到与木块B速度相等，此时弹簧的弹性势能最大。

过程一：子弹C速度大，子弹C打入木块A过程时间短，此过程可以认为弹簧来不及形变。对于子弹C与木块A，在子弹C打入木块A过程认为动量守恒；但此过程属于非弹性碰撞，机械能不守恒，有热能产生、机械能减少。子弹C与木块A相互作用后剩余多少机械能，与上面的例题类同，可根据动量守恒定律与能量守恒定律求解，即

mCv0=(mC+mA)v1

过程二：木块A、木块B、子弹C以及轻质弹簧组成的系统可以看成上面母题中A、B两小球发生弹性碰撞；当轻质弹簧压缩最短时就类同于母题中A、B两小球碰撞中压的最紧，母题中A、B两小球此时速度相等，木块A、木块B、子弹C此时也速度相等。与上面的例题类同，可根据动量守恒定律与机械能守恒定律求解，即

(mC+mA)v1=(mA+mB+mC)v2

解得Ep=160 J

【点评】与上面的母题对比，这道题涉及参与运动的物体个数多、过程复杂，有子弹C与木块A相互作用，还有弹簧连着A与B作用。对此，学生往往无从下手，过程分析不清，规律不能恰当应用；也有些学生可能把问题简单化，没注意到子弹打击木块A过程机械能损失，直接把木块A、木块B与子弹C看成一个系统，应用动量守恒定律求出三个物体一起的末速度和一起的末动能，由此根据机械能守恒，把子弹的初动能减去三个物体的末动能，最终导致出错。我们引导学生对物体分过程归类，再对各小过程应用类似例题的动量守恒定律与能量守恒定律处理，最终得出结论。此道题，要求学生具有过程分析、应用规律等综合能力，能把学过的基本规律、类似题型、小知识模块分别应用到此道题涉及的A、B、C三个物体的各个过程，最终综合求解。

按信息加工理论的观点，垂直迁移是学习者在已有“原问题的知识组块”上加上某一条件来处理一个新的问题，或从已有的知识组块中分离出相对较小的知识组块的信息加工过程。学生垂直迁移能力的关键在于头脑中所贮存关于“原问题的知识组块”的数量和学生对问题的分析能力，而对问题的分析能力体现在学生是否能够从“待处理问题”中分析出解决这一问题所需要的“新知识组块”。垂直迁移的难易程度决定于“原问题知识组块”和“待处理问题”的差异的大小。差异越小，即所需的“新知识组块”越小，迁移越容易。