浅议质点组系统的机械能守恒解题分析

贵州 杨 勇

机械能守恒定律是解决动力学的基本定律，是自然界最普遍的一种能量守恒，机械能守恒的条件几乎包括了功能关系的基本原理，机械能守恒的应用是动力学中的重点及难点，是高考考查的重点知识。所以理解和应用机械能守恒定律是高三复习的重点知识，由于多个物体系统的机械能守恒是多数学生在判断和计算上容易出错的问题，所以本文将从多个物体组成的系统进行分析机械能守恒定律的应用。

一、利用重心分析系统机械能守恒定律的应用

【例1】如图1所示，AB为光滑的水平面，BC是倾角为θ的足够长的光滑斜面，斜面体固定不动，AB、BC间用一小段光滑圆弧轨道相连，一条长为L的均匀柔软链条开始是静止地放在ABC表面上，其一端D至B的距离为L-a，现自由释放链条，求当链条的D端滑到B点时链条的速率v。

图1

【评价】本题是考查学生对质量分布均匀的链条问题的处理，通常此类问题在考试中都以系统机械能守恒的形式出现，主要是考查学生对机械能守恒定律的理解和应用。但是对于此类问题，由于链条不是笔直的，所以在计算时，部分学生会把链条分成两部分来计算，这样链条和链条之间会有张力做功，导致计算错误，所以在练习时一定注意此类问题的系统性。

【变式1】如图2所示，在倾角为θ的光滑固定斜面上，放有两个质量分别为mA和mB的可视为质点的小球A和B两球质量相等，两球之间用一根长为L的轻杆相连，小球B距水平面的高度为h。两球从静止开始下滑到光滑地面上，不计球与地面碰撞时的机械能损失，重力加速度为g。求：当A滑到水平面时的速率vA。

图2

【解析一】由于A、B两球可以看成质点，小球A、B和轻杆组成的系统机械能守恒，当A、B都滑到水平面上时，由于有轻杆连接，所以在水平面上时速度相等，即vA=vB，取水平面为零势面，根据机械能守恒定律有

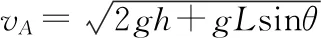
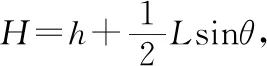
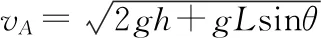
【评价】对于本题的两种解法，结果都是一样的，由于在末状态两小球都到水平面时，其重心的速度与两球的速度大小和方向都一致，也就是相对速度为零，所以两种方法处理最终的结果都对，但是当末状态两小球与重心具有一定的相对速度时，两种解法不一定相等，这涉及质心(即质点系质量中心)运动规律。所以在高考复习中对于此类模型的系统机械能守恒，处理方法一般都用“解析一”的方式求解。

二、利用质心参考系分析系统机械能守恒定律的应用

在高中阶段，我们所遇到的大部分质点系模型的运动大多数是平动，所以我们在选择相应的处理办法时不需要考虑更多的因素，但是偶尔会遇到有转动的情形，所以若用等效重心的方法处理会遇到一些麻烦，下面通过几个实例来分析等效重心处理质点系统机械能守恒时遇到的一些情况。

【例2】如图3所示，在长为L的刚性轻杆的中点A和端点B处各固定一质量为m可视为质点的小球，杆可绕轴O无摩擦转动，求：当杆从水平位置无初速度释放转到竖直位置时，小球B的速度大小。

图3

【解析一】以小球A、B和轻杆组成的系统为研究对象，在摆动的过程中，由于轻杆不会发生形变，所以刚性轻杆不储存能量，整个过程中只有重力对系统做功，因此在轻杆摆动的过程中，只有重力势能和动能之间的转化，因此系统的机械能守恒。摆动过程，两小球做圆周运动，A、B的角速度ω相等，取最低点为参考面，即重力势能为零，由系统的机械能守恒定律得

【评价】此解法是我们在教学以及做题时通常应用的方法，也是高中教辅资料所给出的解析方法，由于在高中阶段，我们所掌握的物理方法较少，所以一般情况下，处理此类问题都用以上的办法，但是由于受到均匀链条类似问题的影响和题型，有的同学为了方便、简单，会选择用重心的方法处理，下面来分析利用重心方法处理是否可以得到相同的结果。

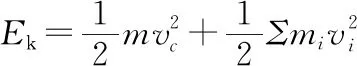
因此可以得到相同的结果。

【变式2】质量都为m的两个小球P和Q，中间用轻质杆固定连接，杆长为3L，在离P球L处有一个光滑固定轴O，如图4所示，现在把杆置于水平位置后自由释放，在Q球顺时针摆动到最低位置时，求：小球Q的速度大小。

图4

【解析一】由于小球P和Q与杆组成的系统只有重力做功，所以机械能守恒，小球Q的重力势能减少，转化成小球P的动能和重力势能以及小球Q的动能，小球Q到达的最低点为参考面，由机械能守恒定律得

由于P、Q绕O点转动的角速度相等，设角速度为ω，则

vQ=ω2L，vP=ωL

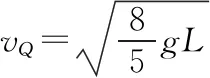
【解析二】找小球P和Q的质心(质量的中心)，由于两小球质量相等，则质心在P、Q连线上中点处，选择Q到达的最低点为参考点，根据柯尼希定理得

【评价】通过以上对两个质点组成系统机械能的两种计算方法的对比，发现求解此类质点组系统机械能守恒问题时，可以通过求解单个质点的机械能的变化，最后把所有的质点的机械能变化关系求和即可，也可以用质心问题进行求解，但是用质心问题时要注意质点组的动能表示形式，其满足柯尼希定理。在高中阶段，我们所研究的基本是单个质点，偶尔也遇到多质点组系统，但是大多数的是平动，所以用单个质点相对基本参考系计算机械能守恒和用质心参考系(高中常表示为重心)计算是一样的，因为各质点组相对于质心参考系速度为零。但是若果遇到像均质杆转动等问题，应用高中常表示的找重心的方法计算就会得到错误的答案，因此我们应用微元等相应的方法解决。

三、利用微元法计算均质杆转动的机械能守恒

在高中阶段微元法的应用比较多，比如均质的细杆其质量可以看成是很多质量元Δmi的叠加，则m=∑Δmi，下面应用微元法处理均质杆类型的机械能守恒问题。

【例3】如图5所示，质量为m的均匀细杆OA，长度为L，从水平位置释放，可绕O点做无摩擦地转动，求：当转到竖直位置时，A端的速度大小。

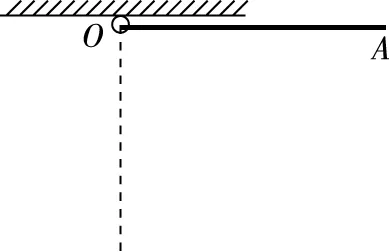
图5

【解析一】对于均匀杆，我们可以看成是一个质点系统，在杆摆动过程中，由于各质点的速度不一样，则不能用质心来代替该杆，我们可以把质量为m的杆分n等份，Δm1，Δm2，Δm3……Δmn每一等份可以看成一个质点，利用各质点相对基本参考系的机械能守恒得

由于vi=ωli，则

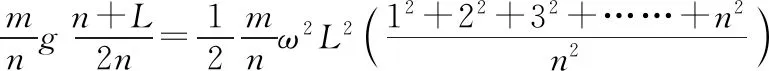
若直接应用重心的方式进行计算，则得到的答案必然是错的。

【解析二】如果取重心，则应用柯尼希定理得

【评价】对于均匀细杆此类型的问题，在高中阶段大多数是平动的，学生在处理的时候有时会想到用重心的方法来简单处理，答案也是对的。但是在教学的过程中，我们要让学生知道，等效重力解决问题的条件性，不要把所有模型都统一用同一种解题方式，这样对学生追求物理规律和科学处理问题的方法存在限制。在教学中，尤其是具有一定数学基础的高中生，我们要尽可能地让学生掌握更多的用数学知识处理物理问题的方法，不要禁固于公式的套用，这样会失去学习物理的意义。