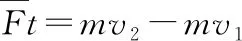“电荷量”求解方法归类例析
2020-11-13河北李晓青
河北 李晓青
电荷量是静电场中常见的一个物理量,又是深入了解静电场的“小导游”,所以求解电荷量成为近几年高考考查的热点。高考对求解电荷量的特点是在不同的物理情境中设计问题,考查学生对电荷量与其他知识的综合运用能力。下面对不同知识背景中求解电荷量的方法进行归纳总结,希望能够对高三物理教师的课堂教学和学生高效学习提供一些参考。
一、利用图象求解电荷量
【例1】某电容器放电的I-t图象,如图1所示,根据此图可估算出电容器释放的电荷量为________C。
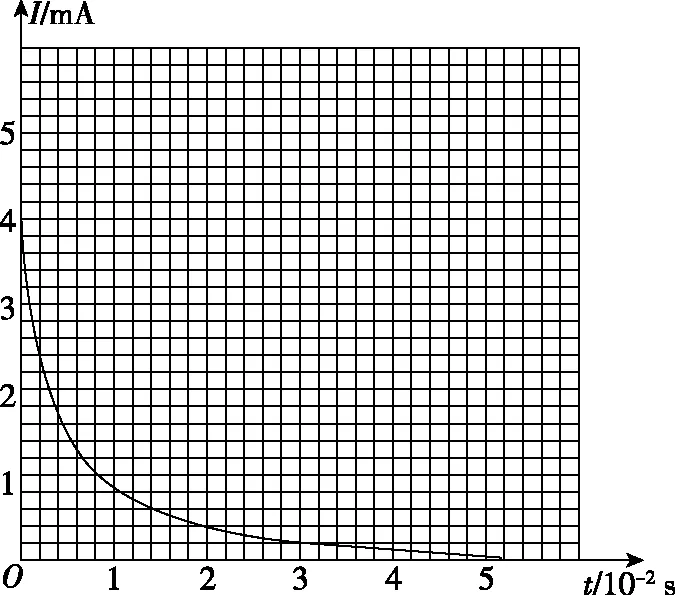
图1
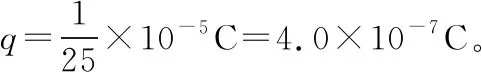
【点评】解决本题的关键是明确图象中的曲线与横、纵坐标所围成“面积”的数值表示电容器释放电荷量的大小,因此,求出“面积”就可以知道电容器放电时释放的电荷量。
【解题策略】针对I-t图象求解电荷量的关键在于能够读懂图象中图线与坐标轴围成的面积表示的物理意义。知道I-t图象的物理含义为表示所求电荷量的多少,从而很容易得出所要求的电荷量。
二、利用电流的定义求解电荷量
【例2】如图2所示,
竖直平面内固定一宽度为L=0.4 m 的足够长的竖直光滑金属导轨,整个空间存在垂直纸面向里、磁感应强度B=1 T的匀强磁场,导轨的电阻非均匀分布。质量m=0.2 kg,电阻可忽略的金属棒PM与导轨接触良好。t=0时刻给金属棒竖直向下、大小为v0=4 m/s的初速度,金属棒恰好以a=2 m/s2的加速度竖直向下做匀加速运动。运动过程中时刻保持与导轨接触良好且水平,取重力加速度g=10 m/s2。为求金属棒下落0.5 m过程中通过其截面的电荷量q,某同学解法如下:

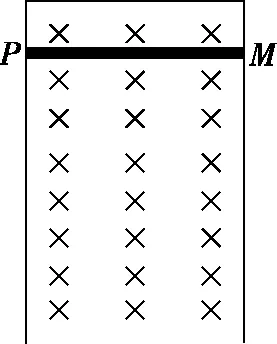
图2

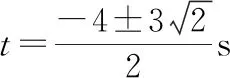
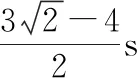
由牛顿第二定律可知mg-BIL=ma
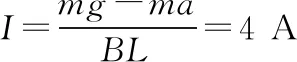
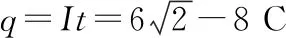

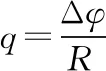
三、借助法拉第电磁感应定律求解电荷量
【例3】如图3中甲所示,平行金属导轨竖直放置,导轨间距为l=1 m,上端接有电阻R1=3 Ω,下端接有电阻R2=6 Ω,虚线OO′下方是垂直于导轨平面的匀强磁场。现将质量m=0.1 kg、电阻不计的金属杆ab,从OO′上方某处垂直导轨由静止释放,杆下落0.2 m过程中始终与导轨保持良好接触,加速度a与下落距离h的关系图象如图3乙所示(g取10 m/s2)。求:
(1)磁感应强度B的大小;
(2)杆下落0.2 m过程中通过电阻R1的电荷量q的数值。
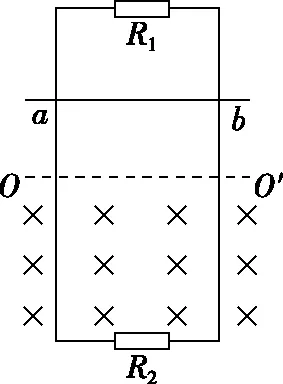
甲
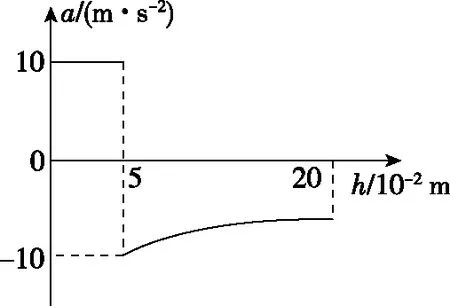
乙
【解析】(1)由图3可知,金属杆自由下落0.05 m后进入磁场,此时的速度、加速度分别为
由牛顿第二定律得mg-F安=ma
回路中的电动势E=Blv
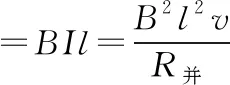
(2)金属杆在磁场中运动产生的平均感应电动势
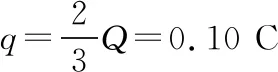
【点评】本题求解电荷量的关键是在电磁感应现象中,穿过闭合回路的磁通量发生改变,在此回路中就会产生感应电流。若回路中的电阻是一个定值,则在一段时间内通过干路的电荷量Q由线圈的匝数n(本题n=0)、磁通量的变化量和闭合回路的电阻R来决定;再结合串并联电流的特点从而使问题得以解决。
【解题策略】对于高中物理中考查图象问题的题目,要明确图象所描述的物理意义;明确式子中正、负号的含义;明确斜率的含义;拐点的意义以及图象与坐标轴围成的面积表示的物理意义;明确图象与物理过程之间的对应关系也是解题的关键所在。而解决电磁感应现象中的电路和图象问题,要明确图象横轴、纵轴代表的物理意义,清楚图象的物理意义,同时要善于从图象中挖掘隐含的条件,借助有关公式、定理和定律做出正确合理的分析和判断,进而求出要求解的物理量。在整个分析过程中,做到严谨推理、全程分析、注意思维的缜密。同时也要注意,针对图象问题进行定量计算时要统一使用国际单位制中的单位。
四、借助动量定理求解电荷量
【例4】(2017年天津卷第12题)电磁轨道炮利用电流和磁场的作用使炮弹获得超高速度,其原理可用来研制新武器和航天运载器。电磁轨道炮示意图如图4所示,图中直流电源电动势为E,电容器的电容为C。两根固定于水平面内的光滑平行金属导轨间距为l,电阻不计。炮弹可视为一质量为m、电阻为R的金属棒MN,垂直放在两导轨间处于静止状态,并与导轨良好接触。首先开关S接1,使电容器完全充电。然后将开关S接至2,导轨间存在垂直于导轨平面、磁感应强度大小为B的匀强磁场(图中未画出),MN开始向右加速运动。当MN上的感应电动势与电容器两极板间的电压相等时,回路中电流为零,MN达到最大速度,之后离开导轨。求:
(1)磁场的方向;
(2)MN刚开始运动时加速度a的大小;
(3)MN离开导轨后电容器上剩余的电荷量Q是多少。

图4
【解析】(1)由左手定则得磁场的方向为垂直导轨平面向下。
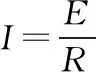
设MN受到的安培力为F,有F=BIl②
由牛顿第二定律可知F=ma③
(3)当电容器充电完毕时,设电容器上电荷量为Q0
则Q0=CE⑤
开关S接至2后,MN开始向右加速运动,速度达到最大值vmax时,设MN上的感应电动势为E′,有
E′=Blvmax⑥
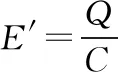

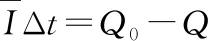
【点评】本题(3)中求解电荷量的关键是通过对整个过程中的平均安培力列出动量定理,同时认识并能够列出平均电流与时间的乘积即为这个过程中损失的电荷量的方程,联立方程,利用数学知识即可求解。