三对角矩阵加箭形矩阵约束四元数矩阵方程AXA*=B 问题研究

吴恒飞，张宗标

（亳州学院 电子与信息工程系，安徽 亳州 236800）

三对角对称矩阵又称Jacobi矩阵，该类型的矩阵在科学领域中具有诸多应用，如力学、工程学等［1-3］；而箭形矩阵的逆特征值问题源于星形弹簧的振动问题［4-5］.矩阵方程是数值代数、科学计算和工程应用等领的域重要研究内容之一，而矩阵方程：

有着许多实际的应用背景，如振动设计、信息论和统计学等，该方程目前已取得了可喜的研究成果，文献［6］利用矩阵的标准分解研究了该方程的对称反自反最小二乘解，文献［7］利用奇异值分解，研究了四元数矩阵方程（1）的Hermitian解，文献［8］研究了四元数矩阵方程（1）在约束条件DX=E下的最小二乘解.利用四元数矩阵的实分解和Kronecker积，给出四元数矩阵方程（1）的自共轭三对角加箭形矩阵解及最佳逼近问题.

表1 符号说明

定义1形如

的矩阵称为三对角加箭形矩阵.若（2）式的元素属于四元数集，则称其为四元数三对角加箭形矩阵，用AQn×n表示全体n阶四元数三对角加箭形矩阵；若A*=A，则称其为自共轭四元数三对角加箭形矩阵；用SAQn×n表示全体n阶自共轭四元数三对角加箭形矩阵；特别情况下，m=1时，其为箭形矩阵，m=n时，其为三对角矩阵.

任意三对角加箭形矩阵可由其3n-2个元素对应确定，对（2）式，记

其中ei为n阶单位矩阵的第i列，容易验证H*H=I3n-2.

引理1A是四元数三对角加箭形矩阵的充分必要条件为vec（A）=H·s（A），即

其中s（A），H如（3）式和（4）式所示.

引理2给定矩阵M，N∈Qn×n，则方程MX=N有解的充要条件是MM+N=N，且方程有解时的通解和无解时的最小二乘解皆可表示为X=M+N+（I-A+A）Y，其中Y∈Qn×n是任意矩阵［9-10］.

问题Ⅰ已知 A，B∈Qn×n，求 X∈AQn×n（X∈SAQn×n），使 AXA*=B.

问题Ⅱ给定是问题Ⅰ的解集.

1 问题Ⅰ的解

设 A，B∈Qn×n，对 A，B 分别进行实分解：A=A0+A1i+A2j+A3k，B=B0+B1i+B2j+B3k，其中 Ai，Bi∈Rn×n（i=0，1，2，3），X=X0+X1i+X2j+X3k，其中 Xi∈Rn×n（i=0，1，2，3）为三对角加箭形矩阵，将 A，B，X 带入（1）式得

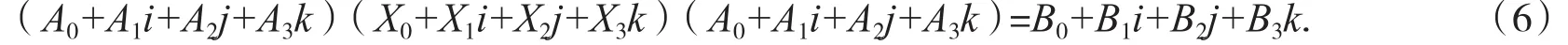
展开（6）式，对比等式两端得如下方程组（7），易知方程组（7）与方程（1）等价.

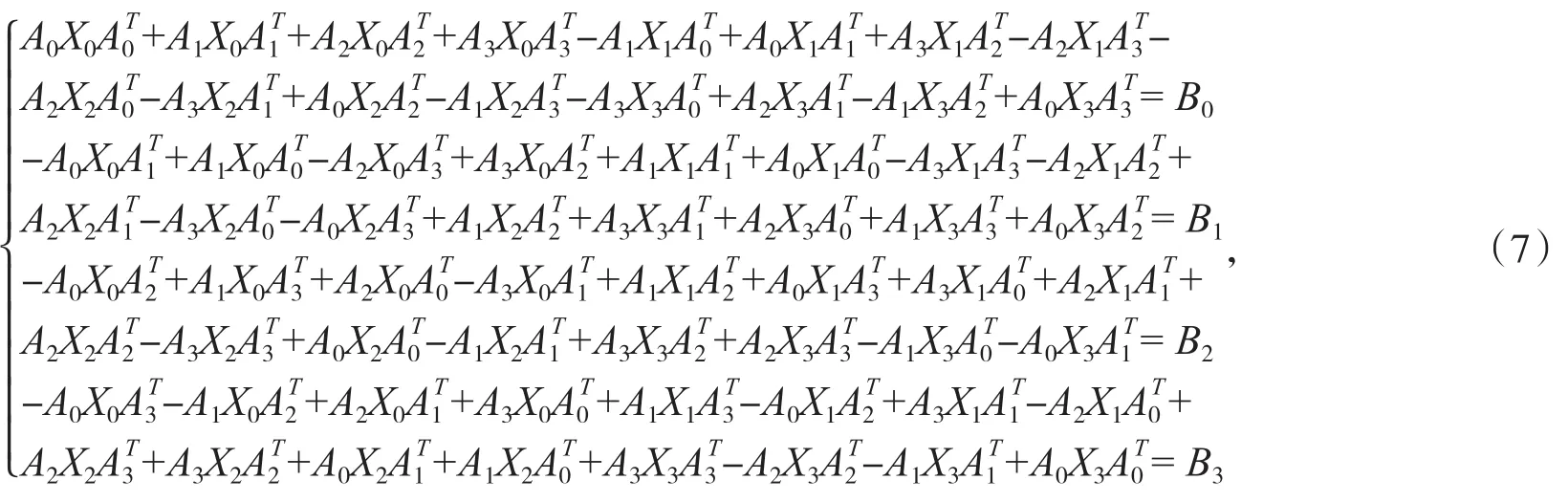
记

其中

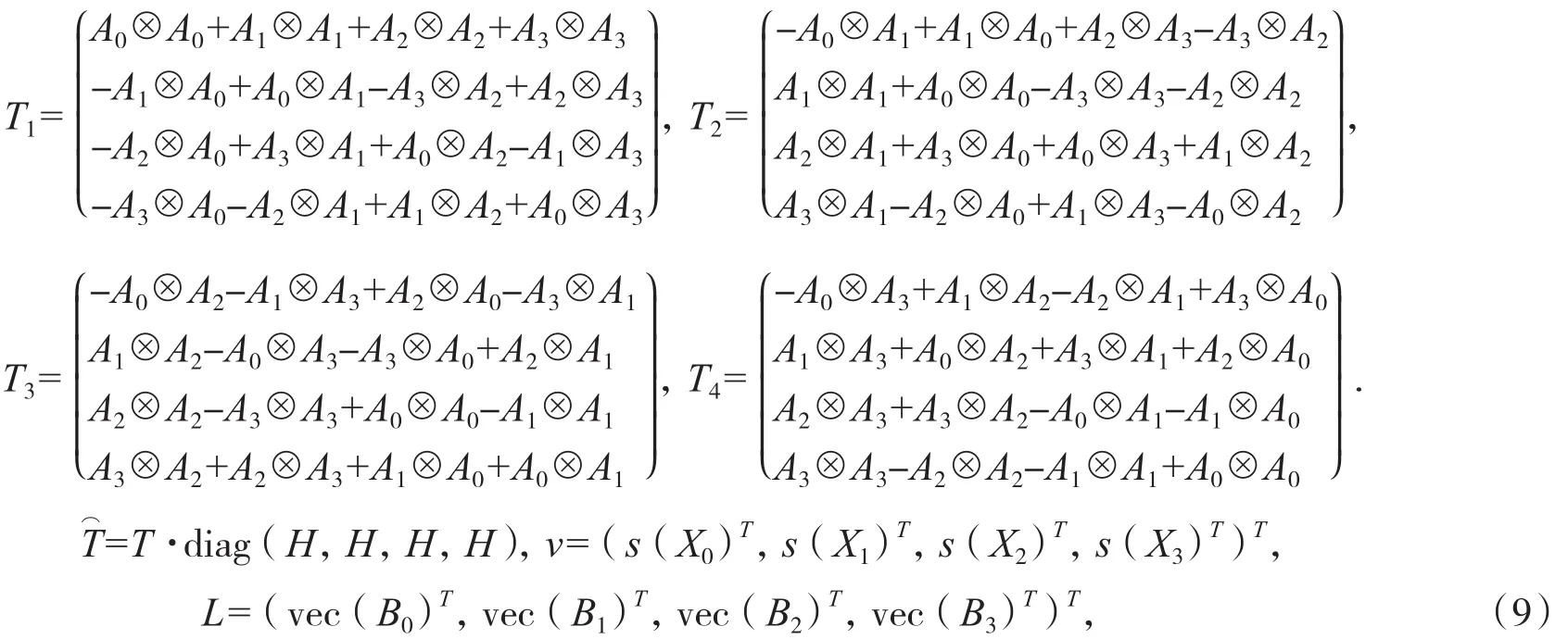
其中 Xi∈Rn×n（i=0，1，2，3）是三对角加箭形矩阵，再根据引理 1 得

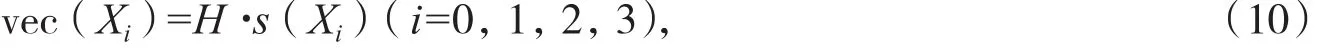
其中 s（Xi），H 如（3）式、（4）式，结合（8）至（10）得（7）等价式为

其中 v∈R（12n-8）×1.

定理1已知矩阵A，B∈Qn×n，方程（1）存在四元数三对角加箭形矩阵解的充要条件为且通解表达式为

其中 v=T︵+L+LT︵Y，Y∈R（12n-8）×1为任意矩阵；vec（Xi）=H·s（Xi）（i=0，1，2，3）；这里 T︵∈R4n2×4（3n-2）、L∈R4n2×1、s（Xi）∈R（3n-2）×1，列矩阵 s（Xi）（i=0，1，2，3）的元素分别取自 v的 1∶（3n-2）、（3n-1）∶（6n-4）、（6n-3）∶（9n-6）和（9n-5）∶（12n-8）行元素.

证明方程（1）有解等价方程（11）有解，由引理2知，方程（1）有解的充要条件为且有解时的通解表达式为 v=T︵+L+LT︵Y，Y∈R（12n-8）×1为任意矩阵，根据（9）式及（10）式的逆拉直运算，得（12）式成立，证毕.

进一步讨论问题Ⅰ的三对角加箭形自共轭解，令

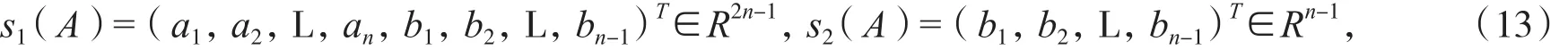
其中ei同（4）式，经计算

引理3对（2）式，记SARn×n（AARn×n）为 全 体 实（反）对 称 三 对 角 加 箭 形 矩 阵 的 集 合，则A∈SARn×n⇔vec（A）=H1·s1（A）（A∈AARn×n⇔vec（A）=H2·s2（A）），其中 H1、H2、s1（A）、s2（A）如（13）、（14）式所示.

对四元数矩阵X进行实分解，形如（6）式，若X*=X，则X0T-X1Ti-X2Tj-X3Tk=X0+X1i+X2j+X3k，所以X0是实对称矩阵，Xi=（i=1，2，3）是实反对称矩阵，根据引理3得

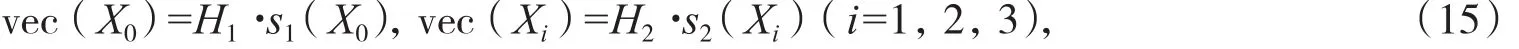
记

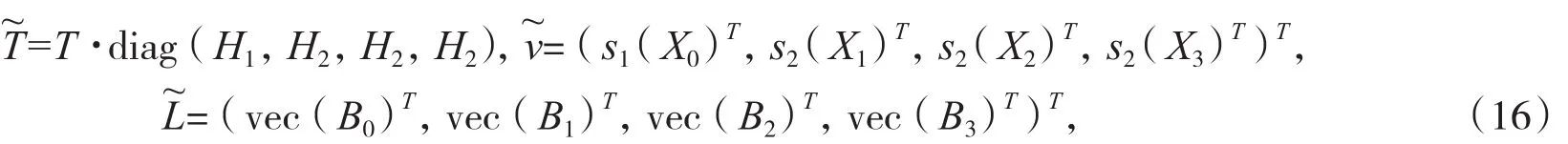
结合（14）至（16）式知，（7）式又可等价表示为

定理2给定矩阵A，B∈Qn×n，方程（1）有四元数三对角加箭形自共轭解且通解表达式为

证明由（17）式与（1）式的等价性，再结合引理2、引理3 知，方程（1）存在四元数三对角加箭形自共轭解的充分必要条件为且有解时的通解表达式为为任矩阵 .再由（15）、（16）式及矩阵拉直运算的逆运算vec-1（Xi）得（18）式成立，证毕.

2 问题Ⅱ的解

设问题Ⅰ的解集SE≠∅，D∈AQn×n为已知矩阵，对D 进行实分解，D=D0+D1i+D2j+D3k，Di（i=0，1，2，3）为实三对角加箭形矩阵，令

定理3D∈AQn×n为已知矩阵，则存在X︿∈SE，对任意X∈SE，有可表示为

其中v︿（i=0，1，2，3），s（Xi）∈R（3n-2）×1的元素分别由v︿的1∶（3n-2）、（3n-1）∶（6n-4）、（6n-3）∶（9n-6）和（9n-5）∶（12n-8）行元素构成 .

证明由（4）式知H*H=I3n-2，再根据定理1知，当X∈SE时，有

所以

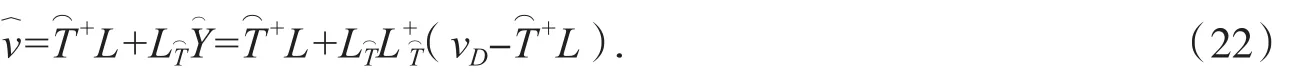
取 s（Xi）（i=0，1，2，3）分别为 v︿的 1∶（3n-2）、（3n-1）∶（6n-4）、（6n-3）∶（9n-6）和（9n-5）∶（12n-8）行元素，结合（12）式可得（20）式成立，证毕.

3 数值算例

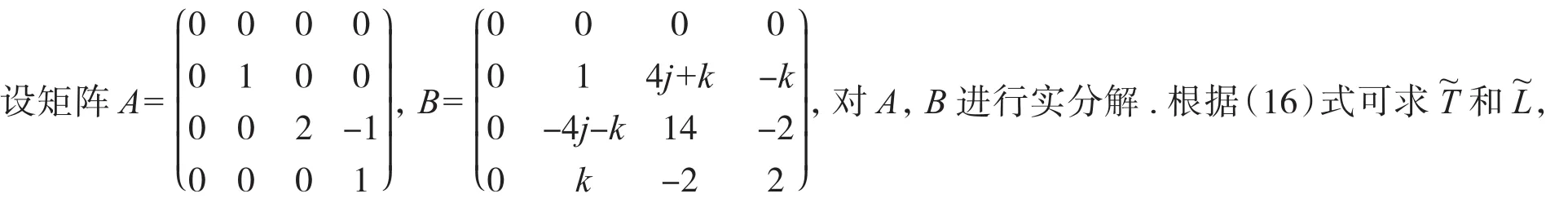
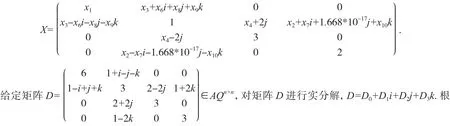
据定理3知，方程（1）对于给定矩阵D，在问题Ⅰ的解集中存在最佳逼近解，结合（3）、（19）及（20）式，可得最佳逼近解为

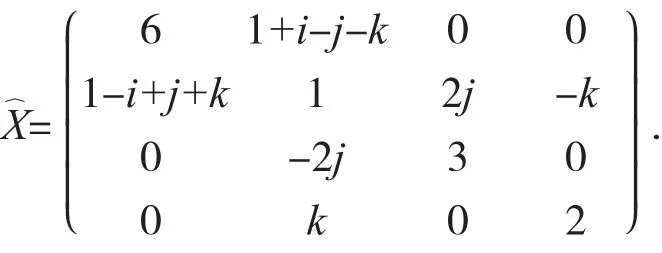
4 结论

提出了矩阵方程AXA*=B的四元数三对角加箭形自共轭解的解决方案.文中给出了对称（反对称）三对角加箭形矩阵的新结构，用矩阵的实分解和矩阵的Kronecker积把方程AXA*=B转化成了无约束的矩阵方程，化解了四元数矩阵乘法不可交换的问题，得到方程有四元数三对角加箭形自共轭解的充要条件和通解表达式，最后在给定的解集中求出了最佳逼近解，这些结论为四元数约束矩阵方程求解问题提供了一定的参考价值.