新课程理念下培养学生数据分析观念的研究

简 艺

（广东茂名幼儿师范专科学校 理学院，广东 茂名 525200）

随着信息社会的发展，数据日益成为一种重要信息，如何收集数据、整理数据和分析数据成为每个公民的基本素养.为此，数学教育中对统计观念的认识越来越重视.在课程标准的制定中，首次把统计与概率列为小学数学内容的四大领域之一，把概率思想方法内容渗透于小学阶段，既体现了统计思想方法的低龄化，又体现了统计概率知识的系统化.随着对课程标准的进一步修订，“数据分析观念”替代了“统计观念”成为核心词.这是基于两个原因：一是内容变革，由单纯的统计知识扩展到统计与概率并存，成为四大领域内容之一，这一领域内容不是“统计观念”所能涵盖的；二是强调“数据分析”的重要性，只有对数据辅以正确的分析才能从中提取相关的信息.那么“数据分析观念”的内涵是什么？课程标准指出，数据分析包括：了解在现实生活中有许多问题应该先做调查研究、收集数据，通过分析作出判断，体会数据中蕴涵着信息；体验数据是随机的有规律的.一方面对于做同样的事情每次收集到的数据可能不尽相同，另一方面只要有足够的数据就可能从中发现规律；对于同样数据可以有多种不同的分析方法，需要根据问题的背景选择合适的方法等.基于上述内涵，如何将数据分析观念的培养与小学统计与概率教学有效结合？笔者作了一些简单的探讨，旨在抛砖引玉.

所谓观念即思想意识，没有意识就没有思维，也就无法形成观念，故培养观念应首先培养意识，数据分析观念亦应如此.

1 数据意识的培养

课程标准修订组组长史宁中教授说：“义务教育阶段统计教学的关键是发展学生的数据分析观念，使他们想到用数据，愿意用数据，能从数据中提取一些信息”.可见数据在统计与概率中的重要性.

1.1 设计问题情境，使学生体会收集数据的必要

标准在第一学段指出：“能根据简单的问题使用适当的方法收集数据，并将数据记录在统计表中”.即要求学生在遇到问题时，首先能想到收集相应的数据.那么在课堂教学中如何创设一个贴近学生生活的情境，以培养学生收集数据的意识？下面是笔者曾经观摩的“最喜欢的儿童节目调查”［1］教学片段.

案例一：

师：同学们喜欢看电视吗？喜欢看什么节目？现在老师播放几段儿童节目主题曲，看谁能猜出儿童节目的名称.（教师播放“七巧板”、“动画城”、“大风车”、“智慧树”的片头主题曲，学生猜.）

师：大家猜得真准！看来同学们经常看这些电视节目，请把你觉得最有趣的内容和增长了哪些知识介绍给大家，好吗？（师生交流后，教师谈话.）

师：通过同学们的介绍，我们知道看电视也可以学到许多知识.现在，我有一个问题：如果要从这4个节目中选一个组织大家看，应选哪个节目呢？（学生表达不同的意见）

师：现在大家的意见不一致，怎么办？

生：我们可以数一数每个节目有多少同学喜欢看，选择最多同学喜欢看的节目播放就行.

师：大家觉得这个方法可行吗？现在我们做一次最喜欢的儿童节目调查吧.

评析：老师以学生经常看的电视节目为素材，激发学生学习动机，提出“如果要从这4个节目中选一个组织大家看，应选哪个节目呢？”交给学生讨论，由于意见不一而导致统计的必要.

1.2 培养学生收集数据的良好习惯

数据的来源有两种：一是现成的，二是自己收集的.学生数据意识的培养不是在课堂上所能完成的，更多的是来自日常生活经验.作为老师，应指导学生收集数据的方法和培养学生收集数据的良好习惯.如生活方面，可鼓励学生收集发生在他们身上的各种数据.如每月测量一次自己的身高和体重，并记录下来，以了解自身发育情况.记录每天休息时间，每天看电视时间等；学习方面，记录各科每次测验成绩，记录数学每次考试由于粗心所丢失的分数，记录每天做家庭作业的时间等.

2 信息意识的培养

2.1 鼓励学生用多种方法整理和描述数据

对于一些原始数据，往往难以直接发现其蕴涵的信息，只有对其进行整理和描述，信息才能被挖掘出来.可见，要提取数据信息，首先要掌握对数据的整理和描述方法.小学阶段对数据的描述方法有：统计表、条形统计图、折线统计图、扇形统计图、平均数、中位数、众数等.课程标准修订意见稿指出：第一学段鼓励学生运用自己的方式（包括文字、图画、表格）呈现整理数据的结果.

案例二：“最喜欢的儿童节目调查”［1］教学片段.

师：现在，老师给每人发一张调查表，请在你最喜欢的儿童节目下面的空格里画“√”.

表1 最喜欢的儿童节目调查一

表2 最喜欢的儿童节目调查二

师：现在发放调查表二，请两位同学上讲台读调查表，其他同学用自己喜欢的方式在表2上记录.注意，不要漏掉，不要重复记录.

（一同学读调查表，另一同学监督，其他学生开始记录，教师用“正”方法记录）

师：谁能把你记录的方法和统计结果汇报一下.

生1：我采用画“√”的方法进行记录，……

生2：我采用画“○”的方法进行记录，……

生3：我采用画“正”的方法进行记录，……

师：对于画“正”字的方法，你们明白吗？我看个别同学还不是很清楚，谁能给他们说说？

接着是师生交流、评价，通过比较体会画“正”字记录数据的优势，最后要求全班学生把正确的统计结果填入手中的表2上……

评析：让学生学会唱票，选择自己喜爱的方式记录数据，既尊重了学生的个性学习，又使他们经历了数据的收集、整理等过程，通过多种形式呈现统计结果，学生体验了解决问题方法的多样性.

2.2 鼓励学生多渠道分析数据获取信息

数据蕴涵着信息，信息是可以通过对数据的分析获取的.那么课堂教学中如何引导学生通过对数据的描述分析获取数据所蕴涵的信息？下面是笔者曾经观摩的“折线统计图”的教学片段.

案例三：“折线统计图”［2］教学片段.

（1）师：请观察图1第23～29届奥运会中国金牌数统计图，你发现了什么？与同桌交流.

生1：我发现第24届中国得的金牌数最少，第29届最多.

生2：我发现第25届和第26届中国得的金牌数持平.

师：你们看出来了吗？你是怎么看出来的？

生3：我是看线的走向，从第25届到第26届，这条线是水平的.（师板书：平——不变）

生4：我还发现从第26届以后，中国队获得的金牌数一届比一届多.

师：每届都在增加，增加的情况怎样？哪一届增加最快？你是怎样看出来的.

生5：第29届，因为这条线最长.

师：你的意思是这条线最陡吧.（板书：陡——变化快）

（2）预测：4年后，第30届奥运会将在伦敦举行.你能预测一下从第29届到第30届这条线怎样走吗？

生1：因为我是中国人，所以我预测这条线应该继续向上走.

生2：我也认为是向上走的，因为从第27届开始，这条折线一直向上走.

生3：我不同意，我预测可能要往下走了，不可能一直上升的.

生4：我认为也要往下走了，因为第29届奥运会在北京举行，我国运动员有天时地利人和的优势.下一届在伦敦举行，运动员从北京飞到伦敦一定很累，会影响成绩的……

评析：通过“你发现了什么？”让学生从不同角度分析解读统计图，多渠道分析数据获取信息.教师归纳出变化规律：平——不变，陡——变化快；通过“预测从第29到30届这条折线会怎么走？”激发学生的学习兴趣，极大地丰富了学生的想象力，同时也培养了学生的分析能力.

图1 第23～29届奥运会中国金牌数统计图

3 随机意识的培养

3.1 让学生体验数据的随机性

所谓随机性就是不确定现象.北师大版教材首先在二年级结合“抛硬币”游戏活动体会“正面朝上”或“反面朝上”是事先不能确定的.进而通过“摸球”试验，体会“一定”、“不可能”和“可能”.其次在三年级通过摸球游戏让学生感受事件发生的可能性是有大小的.教学时应让学生经历“问题——猜测——试验——推测”过程，逐步体验数据的随机性.

3.2 让学生体验数据的规律性

所谓数据的规律性就是对于一个随机事件来说，它发生的可能性大小是由它自身的性质决定的，是客观存在的.这种可能性的大小叫做随机事件的概率，在小学阶段，只能借助概率统计定义，即通过大量试验，如果事件发生的频率稳定在某一常数，则这一常数就是这随机事件的概率.那么这种以频率估计概率的方法是不是“瞎猜”？要试验多少次才能保证这种估计的合理性？在教学设计与课堂教学中又如何体现规律性呢？下面是笔者曾经观摩的教学案例，以餐读者.

案例四：“可能性大小”［3］教学片段.

（1）提出问题，讨论方法

师：袋子里有大小、重量完全相同的黄色和蓝色球共10个，猜猜这两种球各有几个？

生：黄9个，蓝1个；黄8个，蓝2个；黄7个，蓝3个；……

师：能不能想个法子，让我们猜得有把握一些？……

（2）摸球试验，确定多少

把全班学生分成15个小组，每个小组袋里黄球的个数是一样的，蓝球数也是一样的.小组成员轮流摸球，共摸20次.屏幕显示摸球步骤：①摸出一个球，记录后放回；②摇匀重复①；③统计数据，猜两种颜色的球各多少？④教师把统计数据输入电脑.

表3 全班实验结果

让学生根据本组汇报数据猜想结果：黄、蓝球数分别为8，2；7，3；5，5；6，4；……

（3）大量试验，确定比例

通过师生谈话、探讨，决定把15组数据相加，相当于一共摸球300次，然后求得黄球与蓝球之比为0.66∶0.34，据此学生猜想黄球与蓝球数分别为7，3或6，4.

通过教师的课件清晰显示随摸球进程画出的频率变化曲线图.再通过设定摸球次数分别为300、800、2 000、5 000时，让学生观察归纳曲线变化的规律：次数越多波动越小，黄球出现次数与总次数之比越来越接近7/10，由此学生猜测：黄7个，蓝3个.

（4）反思体验，深化理解

让学生打开袋子，数球验证.结果是黄球7个，蓝球3个，得到验证.

评析：此案以学生的4次猜测为主线，让学生经历了随着试验次数的增加，猜测范围逐渐缩小，规律越来越明显的过程.特别是通过电脑模拟摸球的设计，直观高效，有利于学生更好地认识统计规律，使学生在愉悦的情境中学会知识，找到方法，兴趣盎然，让人心悦诚服.

4 方法意识的培养

一是让学生学会根据实际问题设计简单的调查表，学会选择适当的方法（如调查、试验、测量）收集数据.如要了解某班学生双休日时间的安排，具体调查的内容包括学生做作业的时间，看电视的时间，玩手机的时间，和同伴玩的时间，和家长玩的时间以及休息的时间等.调查的方法可以采取逐一填写调查表的方法，通过对这些问题的调查，从中得出某班学生双休日时间的基本情况.

二是让学生学会根据问题的背景选择合适的方法对数据进行描述、分析和推断.如为了解小明出生半年来每月体重变化的情况，调查到小明出生时的体重为3.8 kg，出生至6个月的体重如表4所示.

表4 小明出生至6月的体重

从表4中可直接看出小明出生1～6个月的体重，但不能发现变化的规律.这时自然想到用条形统计图的方式呈现，如图2所示，条形统计图比统计表更直观，可以看出每月的体重都有所增加，但增速难以体现.为更好地体现体重变化的规律，这时不难想到用折线图，如图3所示，不但可看出小明前6个月，每月体重都在增加，而且还明显看到第1个月生长最快，第2个月次之，然后增速逐渐减小，由此还可以预测小明出生后7月和8月的体重.

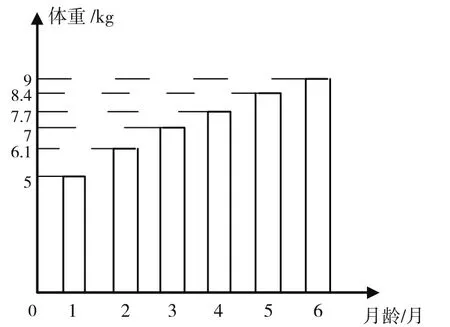
图2 小明出生至6个月体重条形统计图

图3 小明出生至6个月体重折线统计图

5 评价意识的培养

是否具有质疑和评价意识是衡量学生数据分析观念强弱的重要标志.日常生活中，滥用和误用统计数据的情形随处可见，但大多数人对此并没有引起足够的警觉和质疑.因此，结合学生的生活实际，从小加强他们对于不恰当使用统计信息现象的批判意识非常重要.

5.1 鼓励学生对数据的来源、收集和描述的方法以及游戏的公平性进行合理的质疑

现在是信息时代，报纸、杂志、手机、广播、互联网等每天都发布大量的数据信息，以及由此所做出的一系列解释，但这些数据和解释未必都是可信的.这就需要我们做出理智的分析和选择，养成对不合理现象进行质疑的良好习惯.

如学校门口有一游戏机，由两个转盘组成（如图4示）.游戏规则是：分别旋转两个转盘，当两个转盘所转到的数字之积为奇数时，参赌者赢；当两个转盘所转到的数字之积为偶数时，庄家赢.对此老师可组织学生讨论：你认为这游戏公平吗？为什么？如不公平，你能改变某个数据使游戏公平吗？

5.2 鼓励学生对结论进行合理评价

运用部分推断总体是统计的基本思想，推断结果的准确度有赖于样本数据和推断方法.如果个体数据不准确或推断方法不科学，那么推断结果会出现偏差甚至是错误的，所以应鼓励学生对结论进行评价.

如某公司声称其产品的合格率为99.9%，可信吗？怎样评价？

对此可组织学生讨论：（1）产品的合格率为99.9%是什么意思？（2）若产品的合格率真是99.9%，那么正常情况下，要随机抽取多少个产品才会出现一个次品？（3）假如现在我们随机抽取了10个产品就出现了一个次品，你认为该产品的合格率可信吗？

总之，在“统计与概率”教学中，培养学生数据观念是非常重要的.基于“统计与概率”的内容与现实生活的密切联系，一方面，要创设学生熟悉的生活情境，让学生经历数据的收集、整理、描述和分析过程；另一方面，要结合具体问题情境，让学生经历问题、猜想、试验、推测过程，同时要结合具体案例进行分析，注重学生对知识的体验过程.

图4 游戏机转盘