基于多传感器融合的叉车型AGV定位技术研究
2020-11-12钱东海左万权徐慧慧
钱东海,左万权,赵 伟,徐慧慧
(上海大学机电工程与自动化学院,上海 200444)
0 引言
自动导引小车[1](automated guided vehicle,AGV)是现代制造企业物流系统中的重要设备。激光自然导航采用激光雷达扫描环境轮廓,并通过同步定位与建图(simultaneous localization and mapping,SLAM)技术实现AGV的定位与环境地图创建[2]。采用激光SLAM技术对AGV进行定位时,需要对激光雷达采集到的点云进行配准,得到点云之间的相对位姿。针对点云配准,有以下方法。
迭代最近点(iterative closest point,ICP)算法[3]根据两帧点云之间的对应点对关系,求解旋转矩阵与平移矩阵;Andrea Censi在ICP算法的基础上进行改进,提出PL-ICP算法[4];Biber提出正态分布变换(normal distributions transform,NDT)算法[5],求解点云之间的相对位姿;Jinliang Li[6]采用扩展卡尔曼滤波对机器人的编码器预测位姿及激光点云匹配位姿进行融合。
本文以叉车型AGV为研究背景,对AGV运动学进行分析,建立系统的状态方程,并利用无迹卡尔曼滤波算法对预测位姿及NDT激光扫描匹配位姿进行融合,提高AGV的定位精度。
1 叉车型AGV运动学模型
本文研究的叉车型AGV属于单舵轮AGV。单舵轮AGV结构简单、转弯半径较小,由一个舵轮和两个从动轮构成。单舵轮AGV自由度的个数(x,y,θ)大于控制输入量的个数。因此,单舵轮AGV属于欠驱动系统。
AGV舵轮含有驱动电机与转向电机。其中:驱动电机驱动AGV前进;转向电机实现AGV转向,并且驱动电机与转向电机分别装有编码器。从动轮起支撑的作用,用于提高AGV的承载能力。
定义AGV两个从动轮连线的中心O点作为AGV位姿的参考点,AGV运动的方向为AGV局部坐标系X轴的正方向,垂直于AGV运动方向为AGV局部坐标系Y轴的正方向。为了对单舵轮AGV进行运动学建模,对单舵轮AGV提出如下合理的假设。
①AGV始终在水平面上运动,且不会发生滑动。
②AGV舵轮与从动轮是刚性的。
AGV参考点在k时刻的位姿为(xk,yk,θk),(k+1)时刻的位姿为(xk+1,yk+1,θk+1)。AGV相邻时刻运动模型如图1所示。
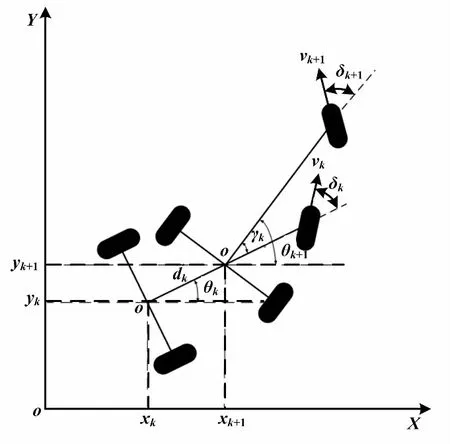
图1 AGV相邻时刻运动模型Fig.1 AGV motion model at adjacent moments
图1中:vk、vk+1分别为k时刻、(k+1)时刻AGV舵轮的线速度;δk、δk+1分别为k时刻、(k+1)时刻AGV舵轮的转向角。
根据k时刻AGV的位姿,可以推算出(k+1)时刻AGV的位姿。单舵轮AGV系统状态方程如下。
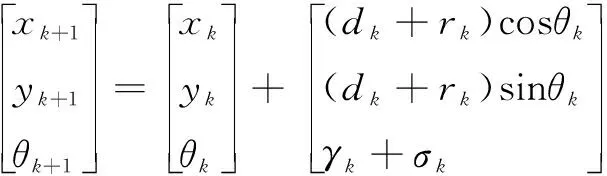
(1)
式中:Xk为k时刻AGV的位姿;Xk+1为(k+1)时刻AGV的位姿;ηk=(dk,γk)T为AGV在采样时间内移动的距离及车体方向角变化量的测量值;wk=(rk,σk)T为测量值噪声。
2 正态分布变换算法
Biber于2003年提出NDT算法用于2D激光点云配准。NDT算法进行点云配准时,无需寻找两帧点云之间的对应点对。因此,NDT算法比ICP算法的效率更高。
AGV运行时,激光雷达在两个相邻时刻采集到两帧点云数据,第一帧为参考帧点云,第二帧为当前帧点云。NDT算法步骤如下。
①将2D空间划分为一定分辨率的网格,根据参考帧点云的笛卡尔坐标,计算每个网格的概率密度函数。
(2)
式中:q为网格中参考帧点云的均值;Σ为网格中参考帧点云的协方差。均值与协方差的计算方法如下。
(3)
式中:xi为网格中参考帧点云的笛卡尔坐标;n为网格中参考帧点云中点的个数。
②根据参考帧与当前帧坐标系之间的位姿关系,对当前帧点云进行齐次坐标变换,将其转化到参考帧坐标系中。
(4)
式中:(x,y)为当前帧点云笛卡尔坐标;(tx,ty,θ)为参考帧与当前帧坐标系之间的相对位姿。
③根据概率密度函数和当前帧点云的笛卡尔坐标,创建目标函数,并采用牛顿法求解目标函数值。当目标函数达到最小值时,当前帧点云在参考帧坐标系中的概率密度最大。目标函数如下。
(5)
NDT算法流程如图2所示。
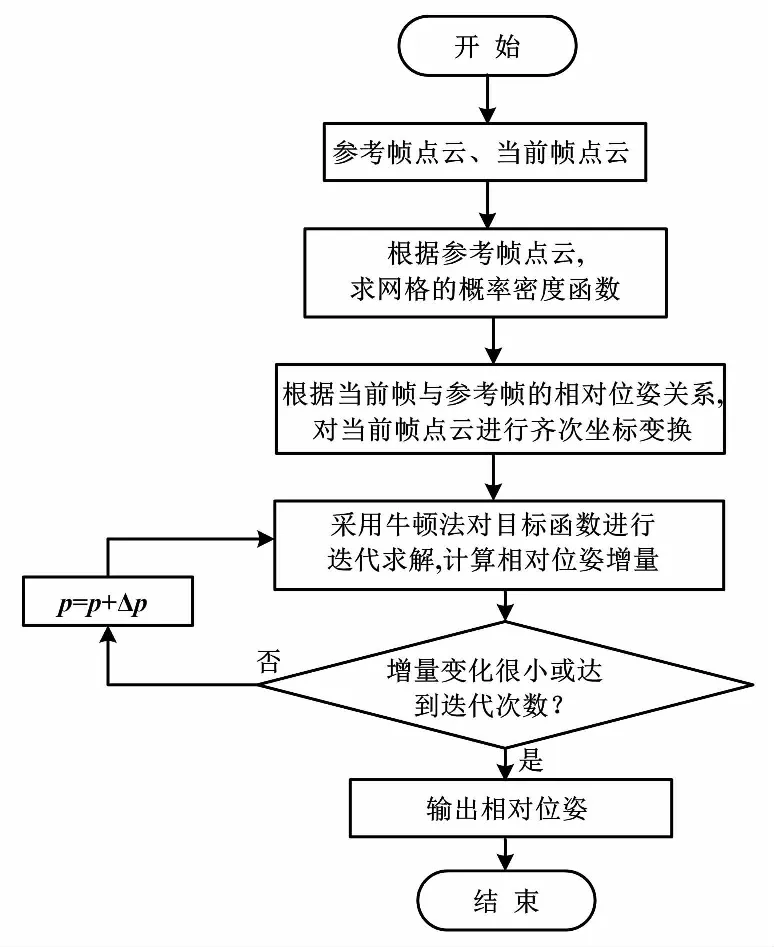
图2 NDT算法流程图Fig.2 Flowchart of NDT algorithm
3 叉车型AGV全局位姿计算
根据NDT算法得到AGV运动过程中参考帧与当前帧的相对位姿关系后,进一步根据参考帧对应的AGV全局位姿,可以计算当前帧对应的AGV全局位姿。参考帧与当前帧关系如图3所示。
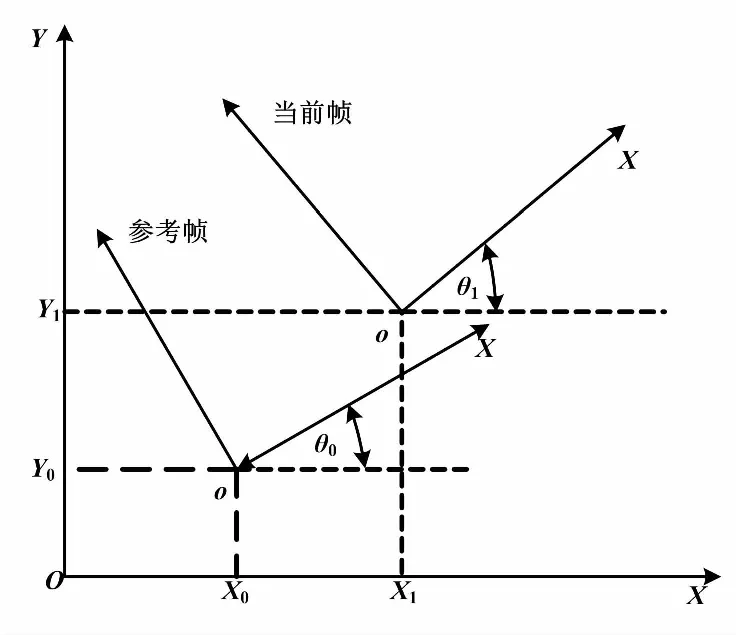
图3 参考帧与当前帧关系图Fig.3 Relationship of reference frame and current frame
参考帧对应的AGV全局位姿为(x0,y0,θ0),当前帧对应的AGV全局位姿为(x1,y1,θ1)。由图3可知,当前帧对应的AGV全局位姿为:
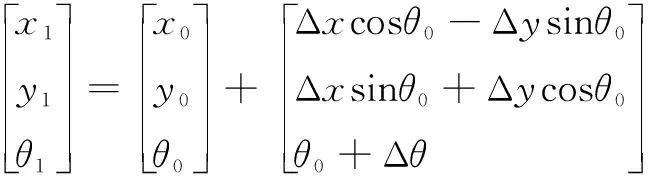
(6)
式中:(Δx,Δy,Δθ)为参考帧与当前帧的相对位姿。
根据式(6)可以计算得到NDT激光扫描匹配位姿。AGV系统观测方程如下:
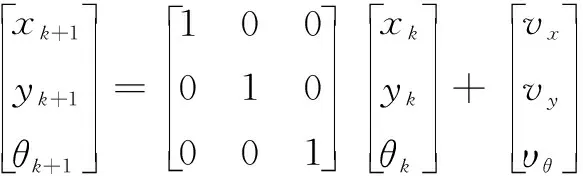
(7)
式中:vk=(vx,vy,vθ)T为观测噪声。
4 改进的正态分布变换算法
本文提出一种改进的正态分布变换-无迹卡尔曼滤波(normal distribution transformation-unscented Kalman filter,NDT-UKF)算法。该算法利用无迹卡尔曼滤波对编码器预测位姿及NDT激光扫描匹配位姿进行融合,以提高AGV的定位精度。
4.1 点云数据预处理
激光雷达扫描到的点云数据主要用于两个方面:定位与环境地图构建。
AGV运动时,激光雷达旋转激光头对周围环境轮廓不断进行扫描,并返回扫描到的点云数据。由于激光雷达自身原因和环境因素的干扰,会产生一些离群点与噪声点。为了提高AGV定位的实时性与准确性,需要对激光雷达返回的点云数据进行离群点移除、滤波[7]等处理,将预处理后的点云数据用于AGV的定位与环境地图构建。
4.2 NDT扫描匹配协方差计算
利用无迹卡尔曼滤波对编码器预测位姿及NDT激光扫描匹配位姿进行融合时,需要计算激光扫描匹配位姿对应的协方差矩阵PN、PN与求解目标函数海赛矩阵的逆矩阵类似。海赛矩阵H各元素的求解方法如下:
(8)
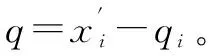
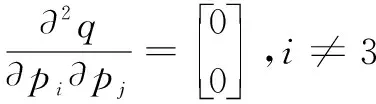
(9)
根据式(8)求得海赛矩阵,进一步可以求得NDT激光扫描匹配位姿对应的协方差矩阵为:
PN=H-1
(10)
4.3 NDT-UKF算法
为了提高AGV的定位精度,本文采用无迹卡尔曼滤波(unscented Kalman filter,UKF)对编码器预测位姿及NDT激光扫描匹配位姿进行融合。无迹卡尔曼滤波以卡尔曼滤波为基础,是一种用于非线性滤波的方法。与扩展卡尔曼滤波的不同点在于,它并不是对系统的非线性方程在估计点处进行线性化处理,而是利用无迹变换(unscented transform,UT)在估计点附近确定采样点,然后利用采样点进行非线性映射,近似得到状态的概率密度函数。这种近似实质上是一种统计近似而并非系统非线性方程的解。采样点的个数通常取(2n+1)个。其中,n为系统状态方程中状态变量的个数[8-9]。
假设AGV在k时刻的位姿为Xk|k,对应的协方差矩阵为Pk|k,测量噪声为高斯白噪声,对应的协方差矩阵为Qk。
NDT-UKF算法步骤如下。
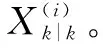
(11)
式中:λ为一个缩放比例参数,用来降低总的预测误差。
②计算7个Sigma点对应的权重值ω(i)。
(12)
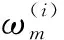
③将步骤①得到的Sigma点代入AGV运动学方程,计算每个Sigma点的k+1时刻的位姿。
(13)
④根据步骤③及式(12),求得(k+1)时刻AGV加权后的预测位姿及对应的协方差矩阵。
(14)
Fw计算方法如下:
⑤根据(k+1)时刻AGV的预测位姿,再次使用UT变换,产生新的Sigma点。
(15)
⑥将步骤⑤得到的Sigma点代入观测方程,得到预测的观测值。
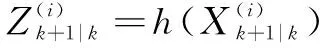
(16)
⑦根据步骤⑥得到的预测的观测值,通过加权得到系统预测的观测值及对应的协方差矩阵。
(17)
式中:Rk+1为观测噪声对应的协方差矩阵,由式(10)得到。
⑧计算卡尔曼增益Kk+1。
Kk+1=PXZPZZ-1
(18)
⑨对(k+1)时刻AGV位姿与位姿对应的协方差矩阵进行更新。
(19)
式中:Zk+1为NDT算法计算得到的AGV全局位姿,由式(5)及式(6)计算得到。
5 仿真及结果
为了验证NDT-UKF算法的定位精度,本文利用Matlab R2019b软件对提出的算法进行仿真分析。Matlab navigation toolbox具有强大的机器人仿真功能,能够对不同类型的机器人进行运动学仿真、路径规划仿真、激光雷达传感器仿真等。仿真过程中,AGV运行环境地图及实际轨迹如图4所示。
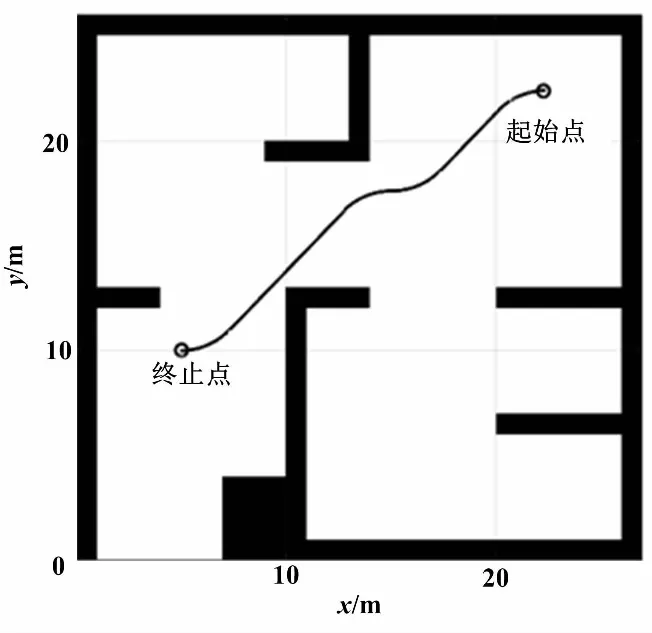
图4 AGV环境地图及实际轨迹Fig.4 AGV environment map and actual trajectory
图4中:AGV运行环境为边长25 m的正方形区域,黑色区域为障碍物,白色区域为AGV可通行区域,黑色曲线为AGV实际运行轨迹。
首先,根据叉车型AGV的运动学模型对AGV位姿进行预测。然后,通过对激光雷达仿真,获取扫描到的周围轮廓的点云数据,并采用NDT算法对点云之间的相对位姿关系及对应的协方差矩阵进行求解。最后,采用无迹卡尔曼滤波对预测位姿及NDT算法求得的位姿进行融合。为了观察NDT-UKF估计轨迹与AGV实际轨迹的误差,选取NDT-UKF估计轨迹的一部分。AGV运行轨迹如图5所示。
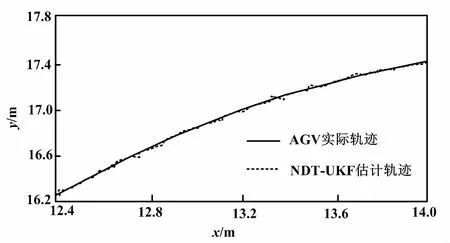
图5 AGV运行轨迹Fig.5 The trajectory of the AGV
为了比较不同算法的定位精度,分别使用NDT-UKF算法、NDT-EKF算法、NDT算法对AGV位姿进行估计,并对估计位姿误差求均值。不同算法定位误差如表1所示。从表1可以看出,本文提出的NDT-UKF算法的定位精度更高。
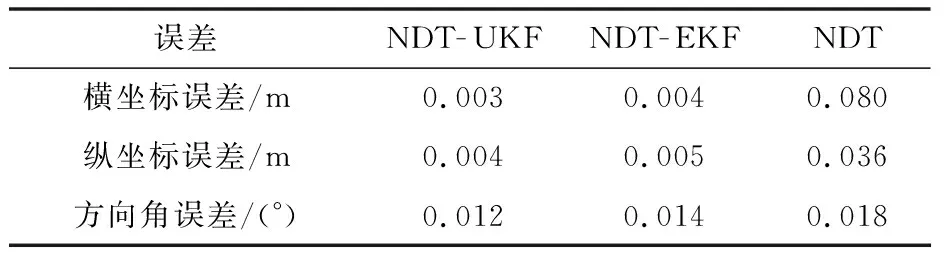
表1 不同算法定位误差Tab.1 Positioning errors of different algorithms
6 结论
本文以叉车型AGV为背景,研究激光自然导航AGV的定位问题。首先,本文对叉车型AGV的运动学进行分析,建立叉车型AGV系统的状态方程。然后,提出NDT-UKF算法。该算法利用无迹卡尔曼滤波对编码器预测位姿及NDT激光扫描匹配位姿进行融合。最后,通过Matlab R2019b软件对提出的NDT-UKF算法进行仿真。仿真结果表明,本文提出的NDT-UKF算法的定位精度更高。进一步工作包括对AGV环境地图创建进行研究等。
