应用重力地质法反演马里亚纳海沟地形

王永康周兴华唐秋华王盼龙姜传苓刘 豪张孝首

(1.自然资源部 第一海洋研究所,山东 青岛266061;2.山东科技大学 测绘科学与工程学院,山东 青岛266590;3.南京大学 地理与海洋科学学院,江苏 南京210023)

海底地形是海洋研究的重要内容,高精度、大范围的海底地形数据是研究海底地理特征、地壳结构、海流、内波等的有力资料。传统的水深数据是通过船载声呐测量获取,尽管声呐精度高,但是作业效率太低,不适合进行大范围的海底地形获取。自从Seasat、Geosat等卫星和Cryosat、ERS任务的成功实施,许多学者利用测高数据,采用最小二乘配置法、逆Stokes法和逆Vening Meinesz法反演了高精度、高分辨率的海洋重力异常[1-5],并将测高重力异常应用到海底地形的反演中[6-7]。重力地质法是利用重力异常反演海洋水深的一种有效方法,最初应用于冰川沉积物下的基岩高程测量[8-9],但是由于地下物质的密度变化,该方法在陆地区域的使用受到了限制,海底洋壳和海水之间密度差变化较小,这使得重力地质法十分适宜于利用卫星测高重力异常反演海底地形的研究[10]。重力地质法已经成功应用于许多海域的地形反演:Roman[11]反演了巴伦支海和格陵兰岛周围海域的海底地形;Kim 和Yun[12]反演了韩国西海海底地形;Kim 等[13]反演了德雷克海峡的水深;胡敏章等[14]反演了皇帝海山的海底地形,并且指出参考深度对反演结果影响有限;欧阳明达等[10]、彭聪等[15]、李倩倩和鲍李峰[16]和Hsiao等[17]反演了中国南海的海底地形;范雕等[18]反演了马里亚纳海沟的海底地形。

利用充足的研究区域水深数据计算不同密度差常数下的水深模型,与检核点对比得到最优密度差常数,在此密度差常数下利用重力地质法对测高卫星重力异常进行海底地形反演,得到1′×1′分辨率的海底地形;通过和船测水深点、ETOPO1模型对比,评估了GGM 模型精度,分析了误差原因。前人主要通过直接观察来判断GGM 模型比ETOPO1模型和直接格网化模型更加精细,本文通过功率谱分析,检测3个水深模型在不同波长下的能量大小,评价3个地形的精细程度,最后通过2条船测水深测线进一步探究GGM 预测水深和实测水深的关系。

1 GGM 原理

重力异常可分为短波重力异常和长波重力异常,短波重力异常是受当地地形起伏的影响而产生,长波重力异常是由地球深层的质量变化引起的。则观测到的海面重力异常[17]:

式中:Δgobs为自由空间重力异常,Δgshort为短波重力异常,Δglong为长波重力异常。

图1是GGM 的原理图,点j n(n=1,2,3,…,k)为水深控制点,根据水深控制点来计算重力异常短波分量,可用布格板公式:

式中:Δgs(j)为j点上的短波重力异常;G 为引力常数(6.67×10-8cm3·g-1·s-2);Δρ为海水和海底洋壳的密度差异常数;E j为j点处的海深;D为参考深度,一般取控制点中最大水深。

控制点长波重力异常可以由观测到的自由空间重力异常减去控制点处短波重力异常计算得出,再把控制点长波重力异常插值生成长波重力异常场,把长波重力异常场从观测的自由空间重力异常场中移除,即可得到测区短波重力异常场。任意一点i的水深值E i为

式中:Δg is为i点的短波重力异常,由测区短波重力异常场通过适当插值方法得到。

图1 GGM 原理Fig.1 Principe of the gravity geology method(GGM)

图2 控制点和检核点分布Fig.2 The distribution of controlling points and checking points

2 海底地形反演

2.1 测区概况及数据准备

马里亚纳海沟是太平洋板块自东向西俯冲于菲律宾板块之下形成的一条向东弧形凸出,近南北向延伸的深沟,北起硫黄列岛、西南至雅浦岛附近,全长2550 km,平均宽70 km,大部分水深8000 m 以上[19]。本文研究区域位于142°36′～147°18′E,23°～27°N,是马里亚纳海沟的一部分,该区域地形复杂,最深约9000 m,最浅约700 m,多海山和海沟,地形起伏大,非常适合用来检验GGM 的反演效果。

船测水深来自NGDC(National Geophysical Data Center)的单波束海深测量数据,因为船测水深存在粗差,数千米深海海域的NGDC 船测水深值只有数百米,经过和ETOPO1模型对比,人工剔除粗差点,最终选取6736个水深控制点和1683个检核点,船测水深控制点和检核点分布均匀且不重复,控制点约是检核点5倍(图2)。测区自由空间重力异常数据来自SIO(Scripps Institution of Oceanography)(图3a),版本为v24.1,与船测重力对比,精度约2 mgal[20],适合用来进行水深反演,船测控制点的重力异常由此内插而得到。检核模型为ETOPO1模型,ETOPO1是由NGDC 和NOAA(National Oceanic and Atmospheric Administration)联合发布的全球地形高程模型,分辨率为1′×1′。

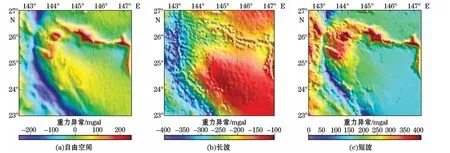
图3 研究区域重力异常Fig.3 Gravity anomalies in the study area

2.2 密度差常数的确定

采用重力地质法反演海底地形时,海水和洋壳的密度差常数的确定是一个关键问题。密度差常数的精确确定,可使短波和长波重力异常从自由空间重力异常中分离出来,确保短波重力异常和水深保持良好的线性关系,由图3可知,短波重力异常和水深有较强的线性关系,长波重力异常和水深的关系不明显。如果密度差常数预测过小,预测海深将会偏大,反之,预测海深将会接近于参考深度[10]。全球洋壳平均密度为2.67 g/cm3,海水平均密度为1.03 g/cm3,因而全球平均密度差常数为1.64 g/cm3,但是局部地形不宜使用平均密度差常数,应该精确估计研究区域的密度差常数。密度差常数一般由2种方法来确定:一种是基于快速傅里叶变换的向下延拓法[7],适用于水深数据缺乏的区域;另一种是利用水深控制点计算不同密度差常数下的水深模型,再与检核点进行比较,得到不同密度差常数下的预测水深和实测水深的相关关系和标准差图,从而得到最优密度差参数[14],这种方法适应于水深数据较多的区域。本研究水深控制点数量充足,所以采用第2种方法,由图4可知,依据标准差较小而相关系数较大原则,密度差常数选取1.20 g/cm3时,标准差为最小值152.9 m,相关系数为最大值0.9943。

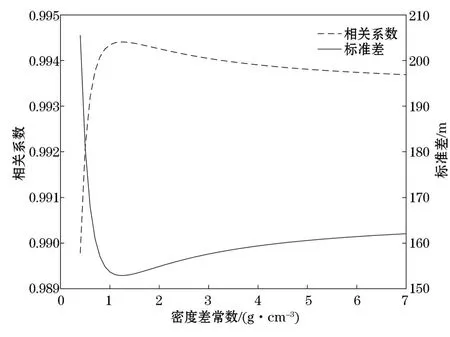
图4 密度差常数确定Fig.4 The determination of density contrast

2.3 GGM 水深模型建立

先根据船测水深控制点,依照式(2)计算船测控制点处的短波重力异常;接着用控制点处的自由空间重力异常减去控制点处的短波重力异常,得到控制点处的长波重力异常,使用GMT(the Generic Mapping Tools)中张力样条函数将控制点处长波重力异常插值得到1′×1′分辨率的测区长波重力异常场(图3b);然后利用测区自由空间重力异常场减去测区长波重力异常场,得到测区短波重力异常场(图3c);再依据式3便可得到测区任意一点的水深值,最终使用张力样条函数插值生成测区1′×1′分辨率的海底地形图(以下称为GGM 模型),见图5b。

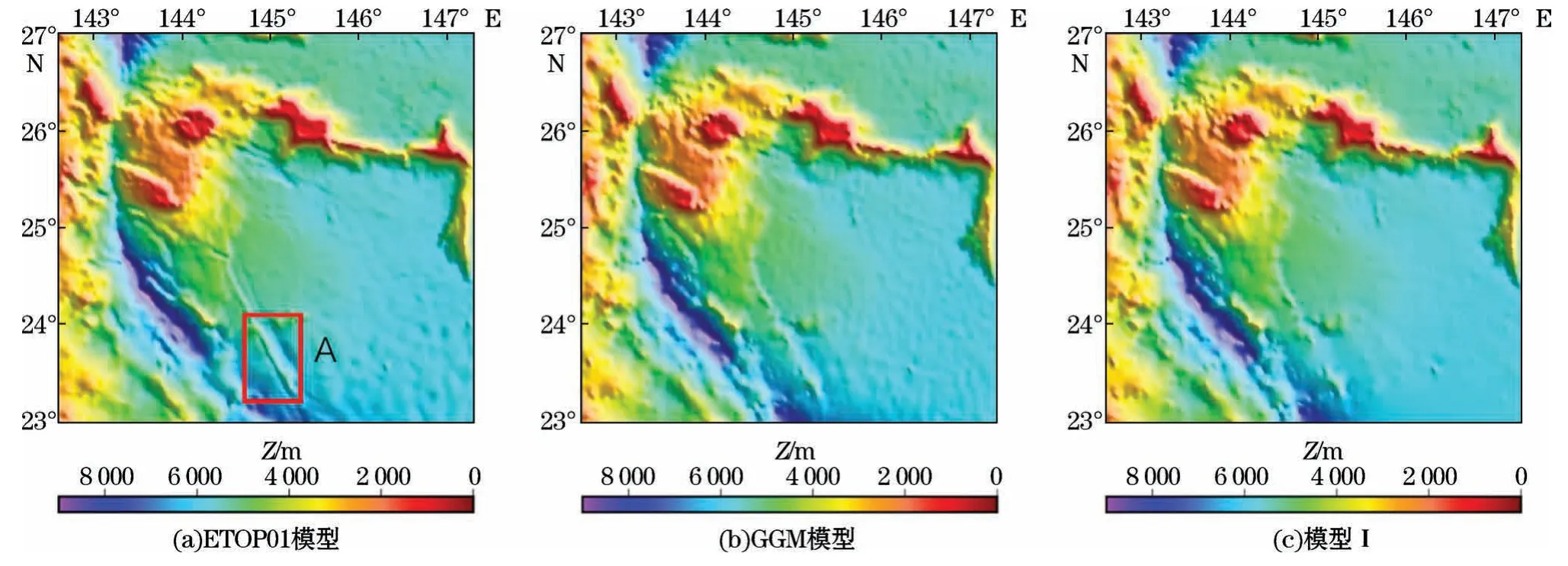
图5 研究区域水深模型Fig.5 Bathymetry model for the study area

3 结果分析

为了对GGM 反演的海底地形进行精度分析,使用了ETOPO1模型、控制点直接插值得到的1′×1′分辨率的水深模型(以下称之为模型I,见图5c)、船测检核点水深和两条测线。

3.1 模型对比分析

首先对GGM 模型、ETOPO1模型和模型I进行统计分析和相关性分析,模型统计和相关性数据见表1。根据统计信息可知GGM 模型、ETOPO1模型和模型I之间的最大值、最小值、平均值等差别很小,表明3个模型的相似度很高。根据相关性分析可知,GGM 模型和ETOPO1模型的相关系数为0.9883,GGM 模型和模型I的相关系数为0.9993,ETOPO1模型和模型I的相关系数为0.9882,3个模型具有很强的相关性。其中,GGM 模型和模型I的相关性更强的原因主要有2个方面:1)GGM 模型是在控制点的基础上建立的;2)原因是控制点分布相对均匀,直接插值得出的模型也可以较好地反映出海底地形地貌,所以两者相关性强。

利用检核点对3个模型进行精度检验,在检核点处内插得出的水深同检核点水深的较差信息见表2。由表2可知,GGM 水深值和检核点水深值较差的标准差和均方根分别为152.9 和153.0 m,相较于ETOPO1模型有着更高的精度。此外,模型I比ETOPO1模型精度高的原因,主要是控制点分布均匀,直接把水深点插值计算也可以获取较为精确的海底地形。GGM 模型和模型I与检核点校差的最大值均超过了2000 m,原因主要有3个:存在粗差水深点未成功剔除,测高重力异常存在较大误差和地形起伏剧烈导致反演精度下降。具体的原因需要根据具体的分析而确定。

表1 GGM 模型、ETOPO1模型和模型I的统计数据和相关系数Table 1 Statistics for GGM model,ETOPO1 model and Model I and their correlation coefficients

表2 GGM 模型、ETOPO1模型和模型I与检核点比较Table 2 Comparison between checking points and models(GGM model,ETOPO1 model,and Model I)

从3个水深模型图对比可知,ETOPO1模型中有一个区域的地形在GGM 模型和模型I上没有清晰表现出来(图5中的矩形区域A),经过和图2对比发现,区域A 控制点分布稀疏,所以未能反演出来区域A 的精确地形,因此,GGM 在控制点分布密集海域的预测精度优于控制点分布稀疏海域。把GGM 模型和ETOPO1模型进行做差处理(图6),从GGM 模型和ETOPO1模型差异图可以清晰看出,在地形变化大的海沟和海山区域,模型之间差距很大;在地形平坦的区域,差距很小。

图6 GGM 模型与ETOPO1模型差异Fig.6 The differences between GGM model and ETOPO1 model

3.2 功率谱密度分析

Kim 等[21]利用功率谱密度法计算了不同水深模型在不同波长下的能量大小,对比不同模型在不同波长下对地形的表现能力,能量越大,说明模型在此波长下对地形表现能力越强。因此,对GGM 模型、ETOPO1模型和模型I进行功率谱密度分析,利用GMT 中grdfft命令,计算3个模型在不同波长下的能量变化,功率谱密度计算方法:

式中:P为不同波长下的能量;PSD为功率谱密度(d B)。本文范围为4.7°×4.0°,所以最大波长约为500 km,结果见图7。图7中以17 km(虚线处)为界分为:在17～500 km 的中长波范围,3种模型表现能力相当;在小于17 km 的短波范围,GGM 模型能量明显大于模型I和ETOPO1模型,表明GGM 对于微小细致的短波地形的刻画优于ETOPO1模型和直接格网化结果。

图7 GGM 模型、ETOPO1模型和模型Ⅰ功率谱密度比较Fig.7 The comparison in power spectral densities between GGM model,ETOPO model and Model I

为了进一步证实功率谱密度分析的结果,把3种模型在检核点处的水深值内插出来并和检核点水深值做差并取绝对值,统计信息如图8所示。根据图8可知,在较差0～100 m 范围内,GGM 模型、ETOPO1模型和模型I所占比例分别是71.95%,59.77%和67.5%;在较差0～300 m 范围内,GGM 模型、ETOPO1模型和模型I所占比例分别为94.76%,85.8%和92.81%;进一步表明GGM 模型比ETOPO1模型和模型I精度更高,对短波长的水深表现能力更强。

3.3 测线剖面分析

为了进一步探究GGM 预测水深和实测水深的关系,本文选择line1和line2两条测线剖面进行分析,测线贯穿整个测区,位置见图9。2条测线既经过地势平坦地区,也经过地势起伏较大的海山和海沟,适合对GGM 模型进行评价。图10为水深剖面,经过对比可知,在海底地形平坦的地区,GGM 反演的水深和实测水深较差很小;当海底地形开始出现起伏后,GGM 预测的水深和实测水深较差便出现较剧烈的变化,进一步表明GGM 在地形起伏较小的区域优于地形起伏较大区域的反演效果。GGM 反演水深和测线水深最大的较差出现在地形起伏剧烈的区域,最大差值约为1500 m,所以本文反演的GGM 模型与检核点最大差值2000多m 的原因是地形起伏剧烈导致反演精度下降。

图9 测线分布Fig.9 Distribution of checking lines

图10 GGM 模型与检查线水深剖面Fig.10 Comparison of profiles between GGM model and checking lines

4 结 语

利用重力地质法反演了马里亚纳海沟的海底地形,经过模型对比、功率谱分析和测线剖面分析,表明重力地质法适合进行大范围的海底地形反演;重力地质法模型在短波长地形地貌的刻画优于ETOPO1模型和控制点直接格网化模型;重力地质法模型精度主要受到密度差常数、控制点分布和海底复杂程度的影响,精确的密度差常数、控制点的均匀分布和平坦的地形均可以提高重力地质法反演精度。所以建议在建立水深模型时候,若控制点分布密集,采用GGM 方法;若控制点分布稀疏,采用ETOPO1模型。

本研究中重力异常数据与船测重力数据存在约2 mgal的误差,若研究区域有船测重力数据,可先把船测重力数据和卫星测高重力数据融合,得到高精度融合重力场,然后再应用于GGM 水深反演,这个方法有待于下一步实验验证。

参考文献(References):

[1]SANDWELL D T,SMITH W H F.Marine gravity anomaly from Geosat and ERS-1 satellite altimetry[J].Journal of Geophysical Research Solid Earth,1997,102(B5):10039-10054.

[2]HWANG C,KAO E C,PARSONS B.Global derivation of marine gravity anomalies from Seasat,Geosat,ERS-1 and TOPEX/POSEIDON altimeter data[J].Geophysical Journal International,1998,134(2):449-459.

[3]ANDERSEN O B,KNUDSEN P.Global marine gravity field from the ERS-1 and Geosat geodetic mission altimetry[J].Journal of Geophysical Research Oceans,1998,103(C4):8129-8137.

[4]KNUDSEN P,ANDERSEN O B.Improved recovery of the global marine gravity field from the GEOSAT and the ERS-1 geodetic mission altimetry[J].Gravity,Geoid and Marine Geodesy,1997,117:429-436.

[5]HUANG M T,ZHAI G J,GUAN Z,et al.On the recovery of gravity anomalies from altimeter data[J].Acta Geodaetica et Cartograpica Sinica,2001(2):179-184.黄谟涛,翟国君,管铮,等.利用卫星测高数据反演海洋重力异常研究[J].测绘学报,2001(2):179-184.

[6]SMITH W H F,SANDWELL D T.Bathymetric prediction from dense satellite altimetry and sparse shipboard bathymetry[J].Journal of Geophysical Research Solid Earth,1994,99(B11):21803-21824.

[7]HWANG C.A bathymetric model for the south china sea from satellite altimetry and depth data[J].Marine Geodesy,1999,22(1):15.

[8]IBRAHIM A,HINZE W J.Mapping buried bedrock topography with gravity[J].Ground Water,2010,10(3):18-23.

[9]NAGARAJAN R.Gravity-geologic investigation of buried bedrock topography in northwestern Ohio[D].Columbus,U.S.:Ohio State University,1994.

[10]OUYANG M D,SUN Z M,ZHAI Z H.Predicting bathymetry in South China Sea using the gravity-geologic method[J].Chinese Journal of Geophysics,2014,57(9):2756-2765.欧阳明达,孙中苗,翟振和.基于重力地质法的南中国海海底地形反演[J].地球物理学报,2014,57(9):2756-2765.

[11]ROMAN D R.An integrated geophysical investigation of Greenland’s tectonic history[D].Columbus,U.S.:Ohio State University,1999.

[12]KIM K B,YUN H S.Satellite-derived bathymetry prediction in shallow waters using the gravity-geologic method:a case study in the West Sea of Korea[J].KSCE Journal of Civil Engineering,2018,22(7):2560-2568.

[13]KIM J W,FRESE R R B V,LEE B Y,et al.Altimetry-derived gravity predictions of bathymetry by the gravity-geologic method[J].Pure and Applied Geophysics,2011,168(5):815-826.

[14]HU M Z,LI J C,JIN T Y.Bathymetry inversion with gravity-geologic method in emperor seamount[J].Geomatics and Information Science of Wuhan University,2012,37(5):610-612,629.胡敏章,李建成,金涛勇.应用重力地质方法反演皇帝海山的海底地形[J].武汉大学学报(信息科学版),2012,37(5):610-612,629.

[15]PENG C,WANG P,ZHOU X H,et al.Bathymetry inversion based on gravity-geologic method in South China Sea[J].Hydrographic Surveying and Charting,2018,38(2):8-11.彭聪,王鹏,周兴华,等.基于重力地质法反演南海海底地形[J].海洋测绘,2018,38(2):8-11.

[16]LI Q Q,BAO L F.Predicting submarine topography of the South China Sea from altimetry gravity field with high precision[J].Hydrographic Surveying and Charting,2016,36(2):1-5.李倩倩,鲍李峰.高精度测高重力场反演南海海底地形[J].海洋测绘,2016,36(2):1-5.

[17]HSIAO Y S,HWANG C,CHENG Y S,et al.High-resolution depth and coastline over major atolls of South China Sea from satellite altimetry and imagery[J].Remote Sensing of Environment,2016,176:69-83.

[18]FAN D,LI S S,MENG S Y,et al.Inversion of Mariana Trench seabed terrain using gravity anomalies[J].Journal of Jilin University(Earth Science Edition),2018,48(5):199-208.范雕,李姗姗,孟书宇,等.利用重力异常反演马里亚纳海沟海底地形[J].吉林大学学报(地球科学版),2018,48(5):199-208.

[19]LIU F L,YANG S X,DENG X G,et al.Depth detection in the Challenger Deep of Mariana Trench[J].Hydrographic Surveying and Charting,2013,33(5):49-52.刘方兰,杨胜雄,邓希光,等.马里亚纳海沟“挑战者深渊”最深点水深探测[J].海洋测绘,2013,33(5):49-52

[20]SANDWELL D T,MULLER R D,SMITH W H,et al.New global marine gravity model from CryoSat-2 and Jason-1 reveals buried tectonic structure[J].Science,2014,346(6205):65-67.

[21]KIM K B,HSIAO Y S,KIM J W,et al.Bathymetry enhancement by altimetry-derived gravity anomalies in the East Sea(Sea of Japan)[J].Marine Geophysical Researches,2010,31(4):285-298.