基于小波变换的海洋地磁日变改正研究

张连伟郑彦鹏*梁瑞才马 龙李先锋刘洋廷华清峰夏成龙

(1.自然资源部 第一海洋研究所,山东 青岛266061;2.青岛海洋科学与技术试点国家实验室 海洋地质过程与环境功能实验室,山东 青岛266061)

海洋地磁测量是海洋地球物理勘探的一种重要手段。海洋地磁日变改正是海洋地磁测量的一个重要处理过程。改正是否准确直接关系到地磁异常值的精确度,从而影响反演、解释等后续工作。《海洋调查规范——海洋地质与地球物理调查》[1](以下简称《规范》)规定:变化幅度小于100 n T 的磁扰日变记录可用于日变改正;磁扰日的日变改正步骤为先用地方时先对平静日变化值改正,再用世界时对磁扰改正[1]。实际工作中,研究人员将日变幅度小于100 n T 的地磁日变化称为磁静日,将磁静日磁扰部分视为随机噪声作圆滑处理消除[2],忽略磁扰部分对磁静日期间日变改正的影响。

现行海洋地磁测量磁静日变改正是将日变站观测值减去该日变站改正基值作为某时刻的日变改正量[3]。《规范》规定:选取地磁平静日的连续24 h观测值,取平均数作为该日变站的日变基值[1]。边刚等[4]提出基时刻或基时段法计算日变基值。李才明等[5]提出分时区加权平均法来确定日变基值。杨震[3]提出应用经验模态分析求取日变基值。这些方法都只是把地磁日变站采集数据减去日变基值作为地磁日变数据进行地磁日变改正,而基值的确定只会引起日变改正量的整体浮动,未能将地磁扰动部分进行分离,无法提高某时刻的日变改正量精度,降低了海洋地磁测量日变改正处理质量。Xu和Kamide[6]提出使用自然正交分量分解地磁日变数据。袁桂平等[7]也利用该方法从地磁日变化中分离静日变化。Janzhura和Troshichev[8]提出一种利用30 d地磁日变数据,分析统计得到24 h的地磁日变数据作为地磁静日变数据的方法,但该方法存在计算效率低、人为主观因素影响大和分析参数不确定性等缺点,不适用于海洋地磁日变改正。陈果等[9]利用卡尔曼滤波技术提取地磁规则日变化,该方法只能定性地提取规则日变化,无法根据处理要求实现目的频段拾取。Cueto等[10]使用Chapman& Miller方法分解太阳日变化和太阴日变化。徐行等[11]利用全球地磁静日模型来计算日变值,该模型[12]精度较差,不适用于高精度的地磁测量日变改正。彭飞等[13]采用傅里叶级数分解地磁日变数据,提出日变数据主要有5 次谐波(周期分别为24,12,8,6 和4.8 h)组成。Yamazaki等[14]利用最小二乘公式将地磁静日变化表达为一个函数,这种方法在日变改正中存在较大误差。刘帆等[15]提出采用最小二乘法代替傅里叶系数计算公式来确定谐波系数,结合傅里叶级数构建太阳静日变化模型。何畅等[16]利用高阶傅里叶拟合对原始日变数据进行滤波处理。对于性质随时间稳定不变的平稳信号,处理的理想工具是傅里叶变换。但是,在海洋地磁日变改正中,地磁日变站采集的地磁日变信号是非平稳的,傅里叶变换不能满足处理要求,而特别适用处理非平稳信号的工具就是小波变换。Heslop[17]利用小波变换分析了古地磁记录与地球轨道/气候变化之间的联系。Klausner等[18]采用一维连续小波变换分析地磁日变特性。Harada等[19]在研究降低地磁扰动对可控源电磁勘探造成的影响方法时,在所有的数据分析过程中都采用连续小波变换代替传统的傅里叶变换。Hattori和Han[20]利用小波变换分析地磁日变的季节性变化。Sid等[21]利用二维连续小波变换研究了磁异常高频信号的固有性质及相关致因源。López等[22]运用小波变换分析地磁暴对中纬度电离层的影响。杨建平[23]运用小波分析方法—小波熵复杂度对地磁观测数据进行了分析。Mandrikova等[24]发现小波变换与自适应平滑相比,可以显著减少在计算地磁活动指数时产生的误差,有效提取地磁水平分量磁扰。李琪等[25]为突出地球磁场短周期变化,选定db5小波作基本小波对地磁台站数据进行二阶小波分解。本文将利用小波变换对地磁静日变数据进行分析和处理。

2 方法原理

小波变换的主要思想是对于一组非平稳信号,基本小波函数进行不同尺度的伸缩与平移作用,信号可经小波变换得到不同尺度因子(频率)下的小波系数。连续小波变换模型公式:

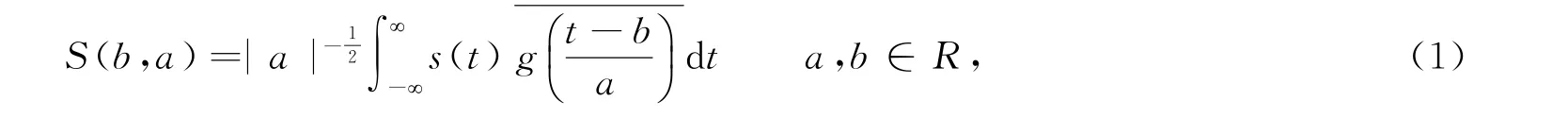
式中:s(t)为原函数;S(b,a)为小波变换后得到的小波系数;a、b分别为尺度因子(伸缩尺度参数)和时间因子(平移尺度参数)与基本小波函数g(t)共轭。

一维离散正交小波变换公式:

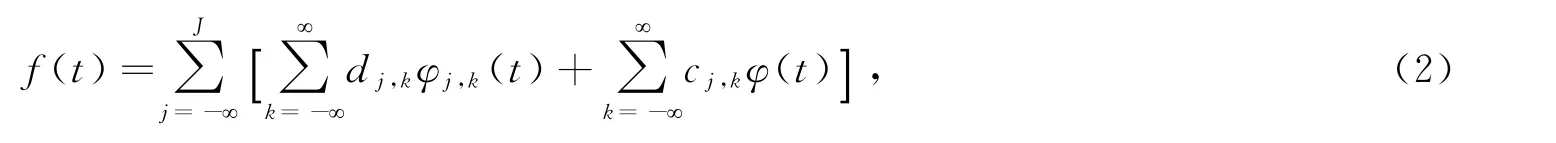
一维离散正交小波分解Mallat算法表达式:

式中:A if(t)为第i层小波分解得到的低频逼近部分,其可进一步分解为第i+1层低频信息A i+1f(t)与高频细节信息D i+1f(t),以此不断分解上一层的低频部分,直到得到所需的频率信息[26]。

根据具体要求,有选择地提取不同阶层(频带)下的小波系数进行小波重构,从而实现不同频带信息的分离(图1),一定程度上起到了带通滤波的作用[27]。

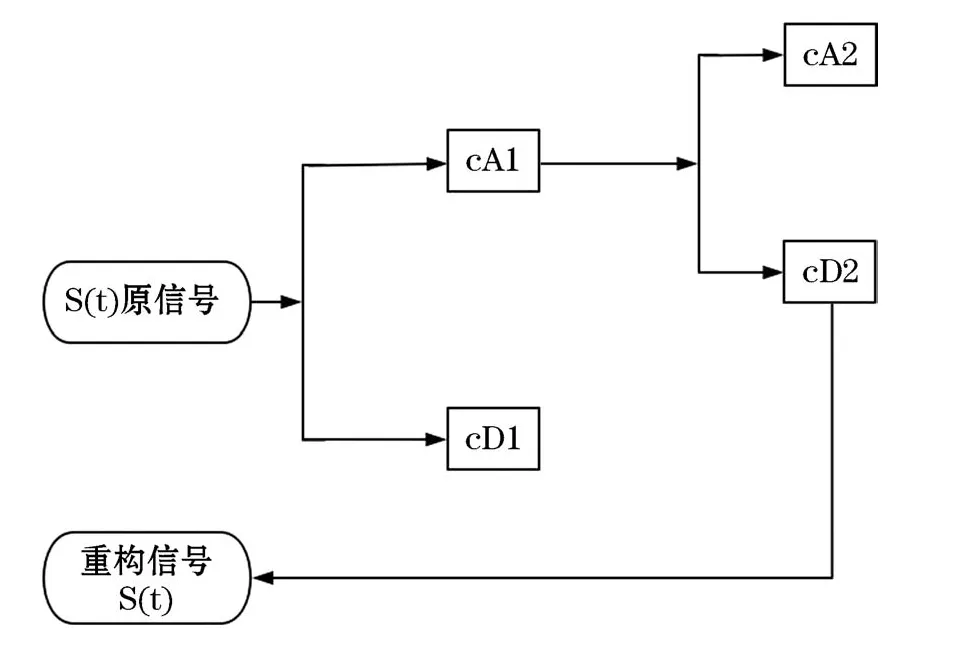
图1 离散小波2层分解与单支重构示意图Fig.1 Sketch of two-level decomposition and single-branch reconstruction of one-dimensional discrete wavelet

小波变换具有时频局部变化特性、多分辨特性、去相关特性和选基灵活特性[28]。傅里叶变换固定选用无限长的正弦波作为基函数,并且积分是从负无穷到正无穷,无论非平稳信号中的哪个频率分量发生变化都会影响全局结果。与傅里叶变换相比,选择具有有限长、急衰性的小波作为基函数的小波变换在分析和处理地磁日变信号时能够更加细致刻画信号的局部时频变化特性,降低个别频率分量变化对全局结果的影响,实现信号成分的精准分离,从方法原理方面提高了地磁测量日变改正方法的科学性。

3 地磁日变曲线特征分析

地磁日变站采集的地磁日变数据是地球基本磁场和变化磁场叠加的总磁场强度。变化磁场又分为长期变化场(一般变化周期为年、几十年等)、短期变化场(主要变化周期为一个太阳日24 h的地磁静日变化)和扰动变化场(磁暴、地磁脉动等)[29-30]。各种变化场的周期、幅度均有差异。其中长期变化和短期变化主要依赖地方时,扰动变化主要依赖世界时。两部分变化时差改正不同,因此无法准确分离磁扰部分数据或忽略磁扰数据的存在都会降低地磁测量日变改正质量。

本研究原始数据均来自INTERMAGNET Programme(http:∥www.inter-magnet.org),原始数据信息:台站编码Alibag(ABG,72°52′19.2″E,18°38′16.8″N),采样间隔为1 min,采样时长20 d(2019-03-01—20)。

本研究以地磁日变站数据平均值作为日变基值为例,对日变改正量(为区分方便,以下称为原始数据)做进一步研究。原始数据做圆滑处理后,消除仪器噪声(图2),数据采样间隔为1 min,采样率为1/60 Hz(因采样率较低且日变数据周期较长,为方便描述,以下频率均扩大3600倍)。

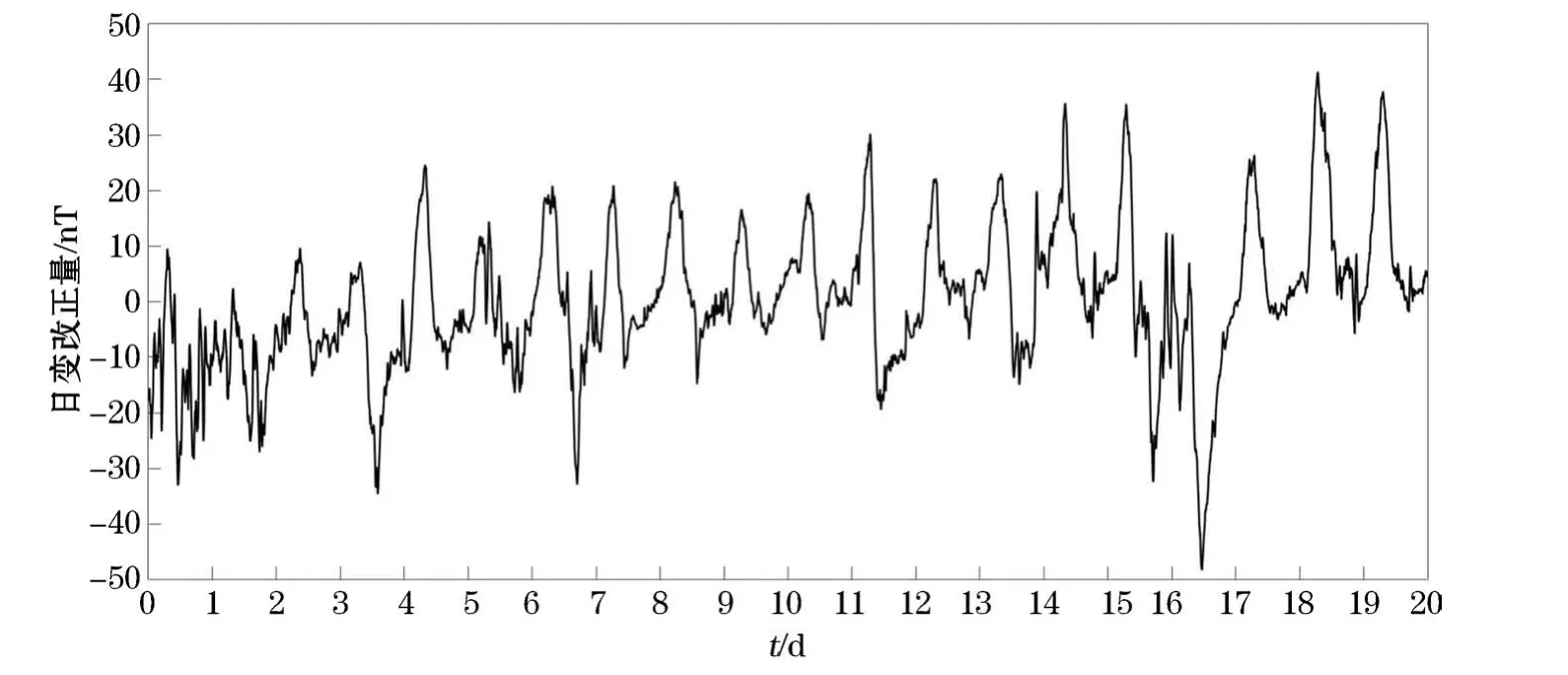
图2 地磁日变原始数据曲线Fig.2 Curve for original data of geomagnetic diurnal variations

从图2可知,地磁日变原始数据最大差距小于100 n T,为地磁静日变数据。经过圆滑处理消除仪器噪声后,数据曲线较规则,但仍包含高频信息。该20 d数据包含2段较异常数据:第1～2天原始数据曲线变化较剧烈;第15～17天原始数据曲线幅值较低且变化较复杂。图3和图4分别为傅里叶变换后的频谱图和能量分布图,地磁静日变原始数据频率主要分布在0～0.4 Hz,其中突出表现在接近零频段和0～0.2 Hz的3个频率。在功率谱上同样可以看到这4个突出能量的分布。除接近零频段区域外,能量分布呈随频率增大能量变小趋势。大于0.2 Hz频段有频率反应,但能量很弱。初步推测接近零频段为长期变化磁场的体现,0～0.2 Hz的3个突出频率为3次谐波(从左到右周期分别为24,12和8 h)的体现,大于0.2 Hz频段为中小幅度地磁扰动变化场的体现。

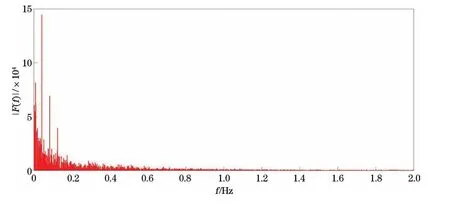
图3 地磁日变原始数据频谱Fig.3 Frequencies of original data of geomagnetic diurnal variations

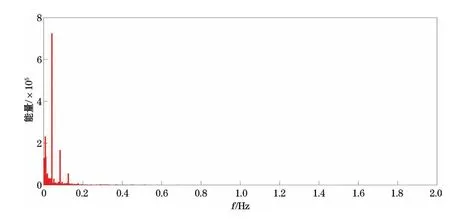
图4 地磁日变原始数据功率谱Fig.4 Spectrum of original data of geomagnetic diurnal variations

Morlet小波表达式:

式中,t为时间。由于morlet小波(式5,图5)没有尺度函数,而且是非正交基本小波,经一维连续小波变换后能够得到平滑连续的小波振幅。因此,选定morlet小波作为基本小波构建连续小波基函数对地磁日变原始数据时间序列进行一维连续小波多尺度分析(式2),小波振幅的平方表示数据能量大小。图6展示了地磁日变原始数据频率域的能量分布。

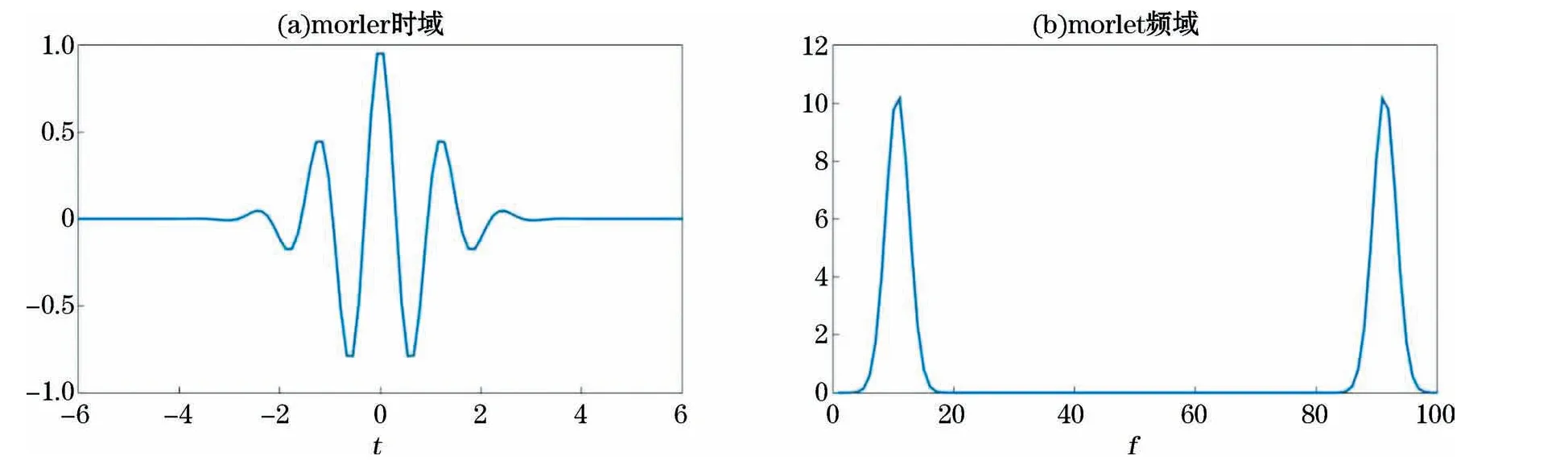
图5 morlet小波时域和频域波形Fig.5 Time domain and frequency domain waveform of morlet wavelet

图6 地磁日变原始数据能量分布Fig.6 Energy distribution of original data of geomagnetic diurnal variations

能量主要集中在24 h周期和12 h周期,在8 h周期也能看到能量局部分布表现。短周期能量分布无规律,但能量一般很小。周期大于24 h的地磁长期变化场能量分布均匀。从图2观察到的第1～2天和第15～17天两端较异常数据在图5中均得到体现:第1～2天数据24 h周期能量不集中且小周期处能量较大,推测该时间段地磁日变原始数据受到某种异常的干扰,因而产生数据曲线变化较剧烈;第15～17天数据周期大于24 h处的能量反应较大,推测是长期变化场异常的体现,为偶然事件,与图2中该时间段异常数据相稳合。周期小于6 h的变化场能量分布呈现能量小、不均匀和无规律特点,满足地磁扰动变化特征,判断其为磁扰变化场。结合图3和图4,可得出大于0.2 Hz的频段即为地磁扰动场在频域的表现。图7是20 d数据总能量分布展示,从中可知周期小于0.2 h的变化场能量很小,可以忽略。随着周期增大,能量增大。在周期为12 h处达到第1个峰值,在周期为24 h处能量达到第2个峰值,也是能量最大值。该现象验证了短期变化场主要由周期为24 h和12 h的变化组成的。图7也展示了周期大于24 h 的长期变化场能量较大,是地磁静日变化的重要部分,对海洋地磁数据日变改正有重要作用,因此忽略长期变化场的日变改正处理方法也是不合理的。

图7 地磁日变原始数据总能量分布Fig.7 Total energy distribution of original data of geomagnetic diurnal variations

4 结果与讨论

4.1 离散小波处理

根据地磁静日变数据特性,使用一维离散小波对原始数据进行分解与重构,提取0～0.2 Hz频段信息即周期＞5 h的地磁静日变数据信息。根据一维离散小波变换Mallat算法(式4)可知,每层低频信号和高频信号是由上层低频信号按频段长度均分所得。经计算,一维离散小波分解至第7层时低频部分代表信号0～0.23 Hz频段,满足提取原始数据目标频段要求。选定的基本正交小波不同,离散小波处理结果可能不同。基本正交小波主要根据数据性质、应用目的和处理效果进行选择。经过对多种基本小波进行试验,发现sym8小波更适用于地磁日变数据的处理。例如:sym8小波(图8)与db5小波处理效果相比,0.3～0.4 Hz频段响应更小,甚至b中大于0.4 Hz频段仍有微弱响应(图9)。该现象在功率谱图中也有体现,图8a比图8b中0～0.2 Hz频段能量更加集中,大于0.4 Hz频段无明显能量响应。在目标频段数据图第1～2天和第6～7天数据段中,可以明显看出sym8小波处理数据曲线比db5小波更加圆滑。因此,选定sym8小波作基本正交小波函数。

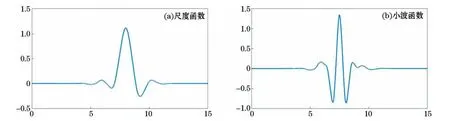
图8 sym8小波尺度函数和小波函数波形Fig.8 Waveforms of sym8 scale function and wavelet function

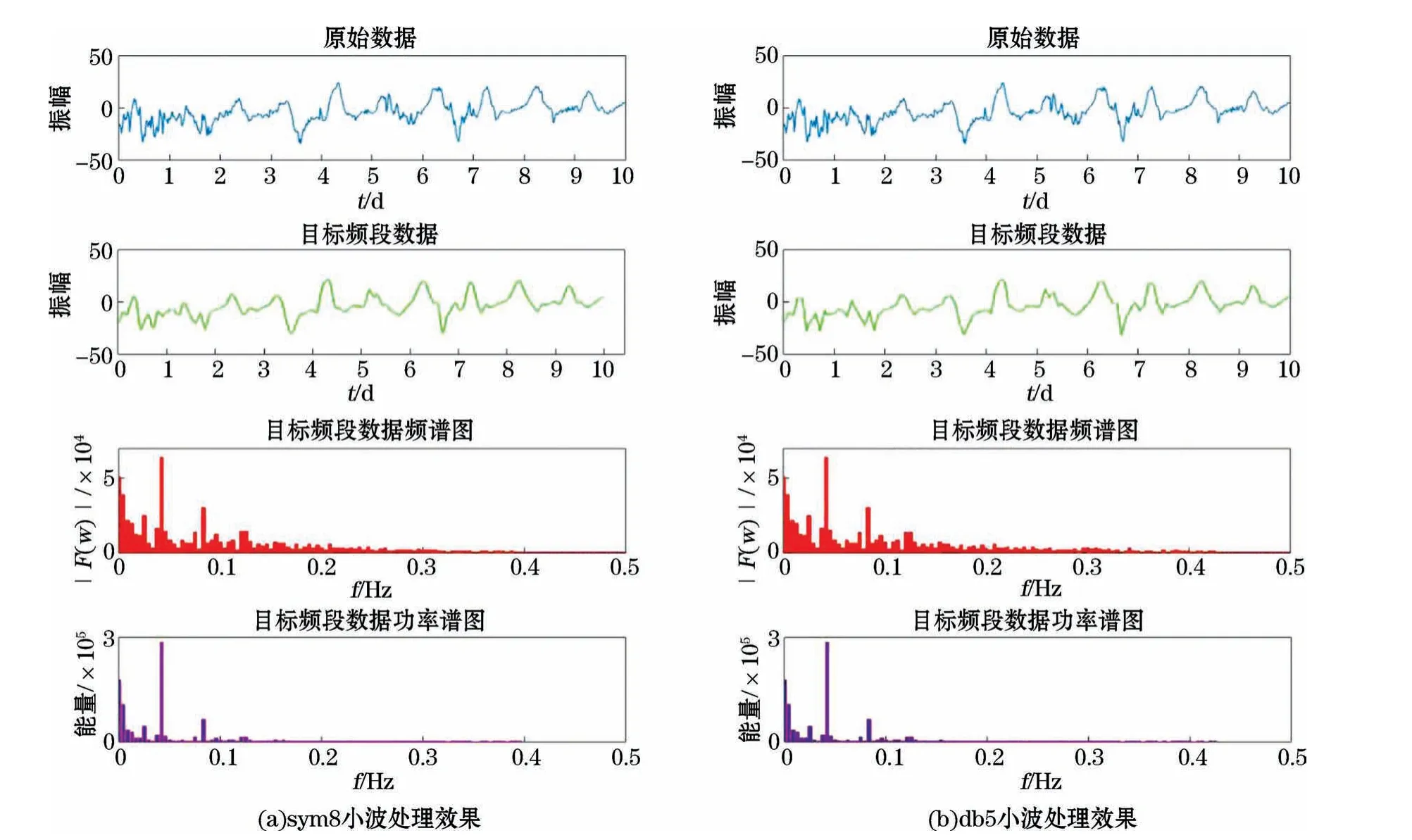
图9 sym8小波和db5小波处理效果对比Fig.9 Comparison of the processing results of sym8 wavelet and db5 wavelet

图10 处理后地磁静日变改正曲线Fig.10 Geomagnetic diurnal variation correction after processing

对表1中20 d地磁静日变化数据使用一维离散小波变换进行7层分解,提取第7层小波分解低频系数,进行单支重构,得重构信号,即处理后地磁静日变改正数据(长期变化和短期变化数据),见图10。原始数据与处理后地磁静日变改正量差值为磁扰部分数据(图11)。

图11 磁扰数据曲线Fig.11 Magnetic disturbance data curve

4.2 处理数据评价

经过一维离散小波分解和单支重构处理后,得到地磁静日变改正数据。为验证处理效果,将地磁静日变改正数据与地磁静日变数据进行对比(图12),处理后数据与原始数据总体趋势一致。在原始数据曲线变化规则段,如第2～13天,处理后数据曲线和原始数据曲线几乎重合,基本保留了原始数据信息;在第1～2天不规则段,去除了高频成分,保留中、低频成分;第15～17天,处理前后数据曲线高度吻合,保留了长期变化场数据。数据两端无明显边界效应现象,保证了数据的保真度。

对经处理得到的地磁静日变改正数据进一步分析,分别作傅里叶变换和一维连续小波变换,在频率域和小波域进行分析。

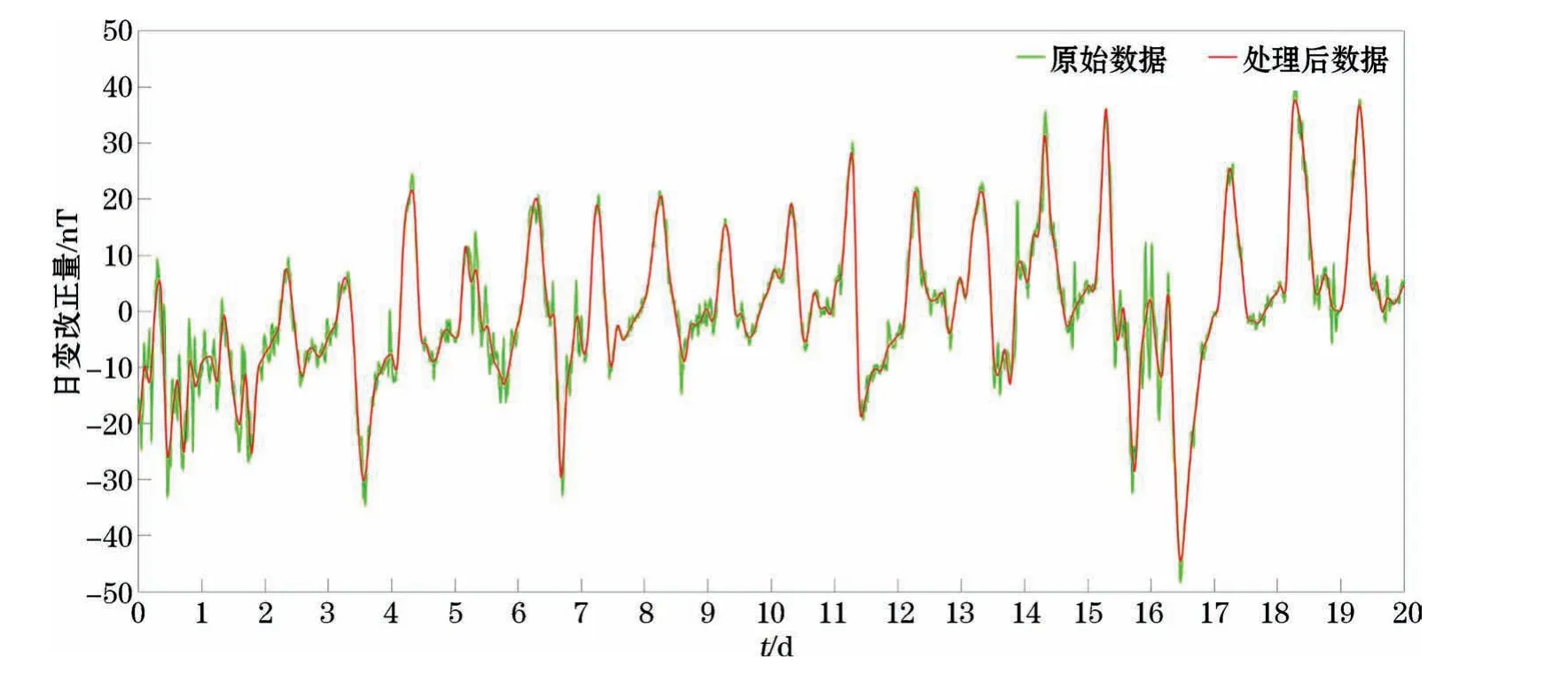
图12 处理前后数据对比图Fig.12 Data comparison between before and after processing

在图13频率谱和图14功率谱中,处理后数据几乎完全保留了4个突出频段和低频的能量,即地磁静日变改正数据:长期变化和短期变化。一维离散小波变换处理完整地去除了大于0.4 Hz的高频信息,而对于0.2～0.4 Hz频段,虽有频率表现,但在功率谱上能量几乎为0,可以忽略。该结论在图15和图16中得到进一步证实:与原始数据的小波域能量分布图相比,高频能量消除,长期变化和短期变化能量得到保留,整体能量分布与处理前基本一致。由此可得,对地磁静日变数据做一维离散小波分解与单支重构可将两个频段信息较完整地分离,得到地磁静日变改正数据和磁扰数据。

图13 处理后数据频谱Fig.13 Frequency data after processing

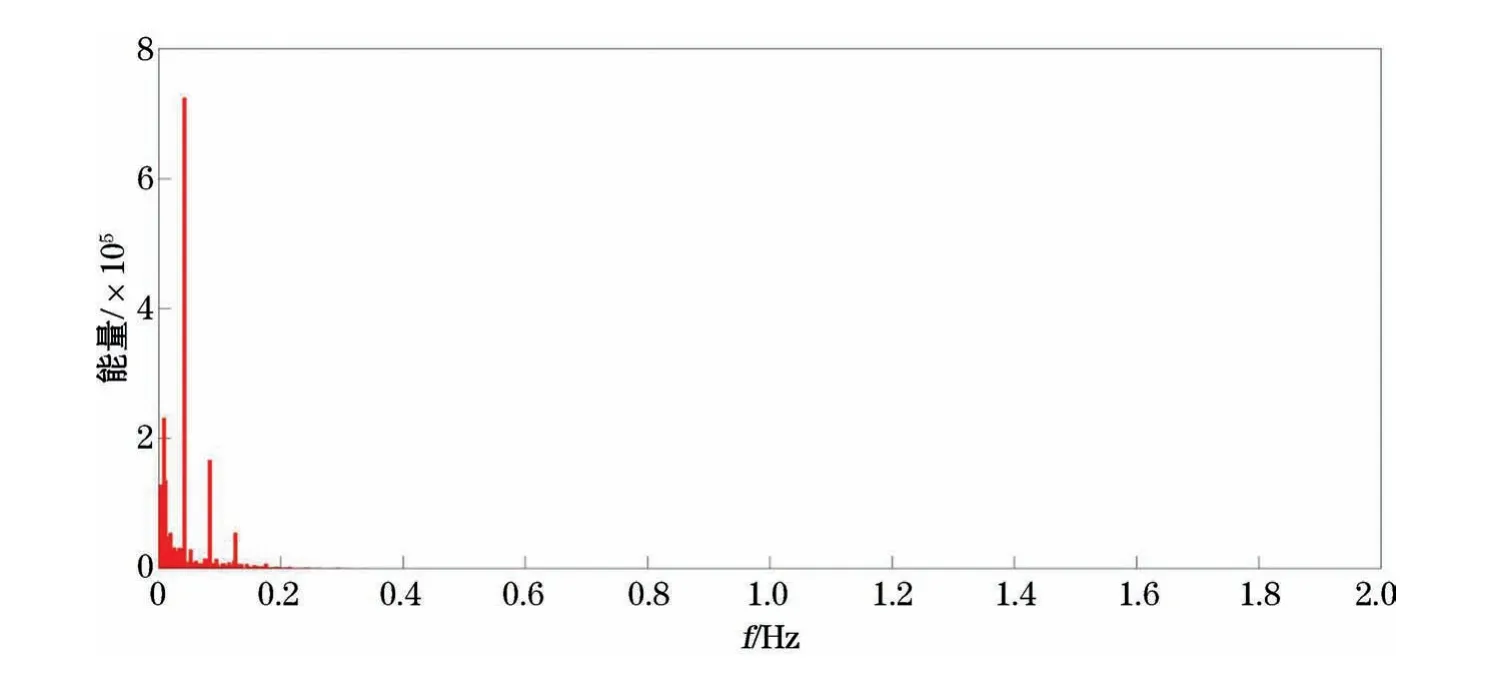
图14 处理后数据功率谱Fig.14 Spectrum of data after processing

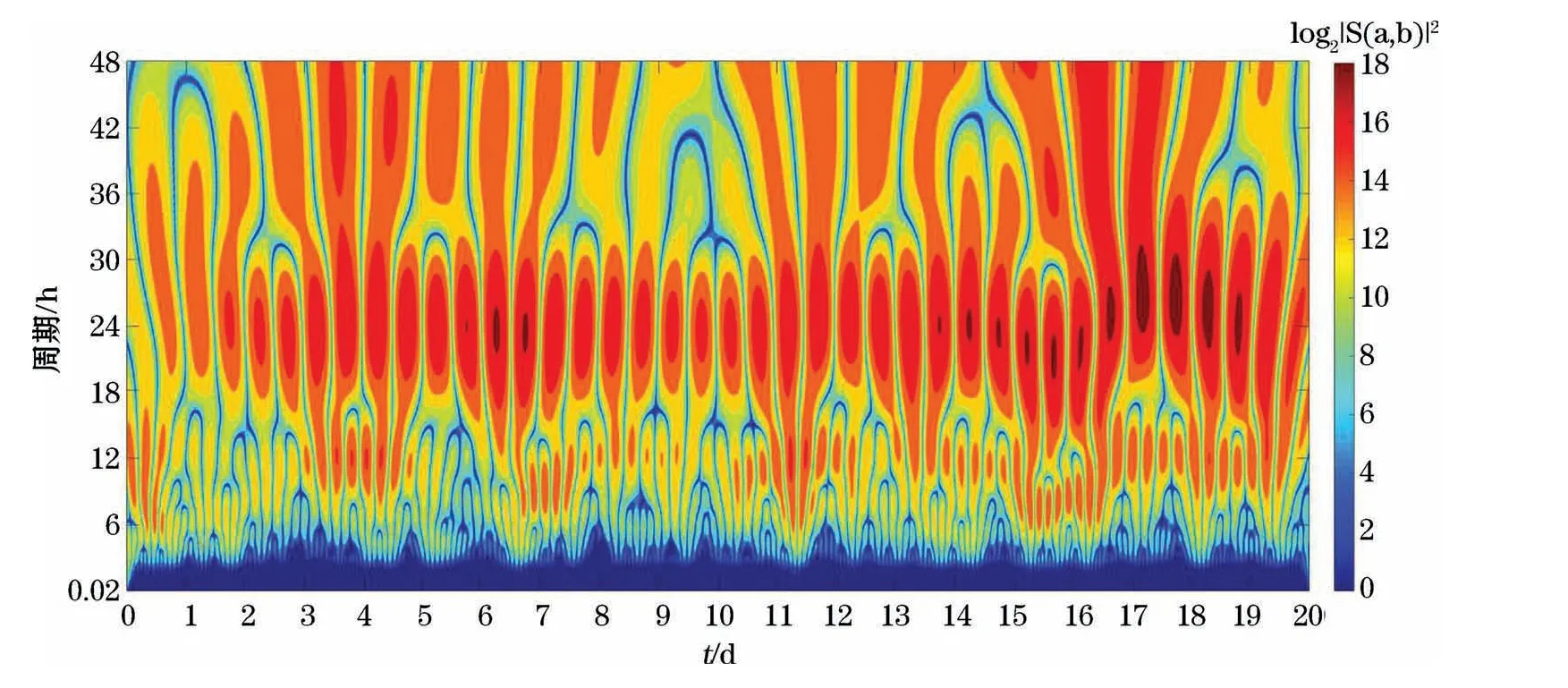
图15 处理后地磁日变改正数据能量分布Fig.15 Energy distribution of geomagnetic diurnal variation correction data after processing

图16 处理后地磁日变改正数据总能量分布Fig.16 Total energy distribution of geomagnetic diurnal variation correction data after processing

地磁静日变短、长期变化部分和磁扰部分分别依赖地方时和世界时,可依照磁扰日变改正法[1]进行分别改正:用地方时对地磁静日变改正数据进行改正,然后再用世界时对磁扰数据进行改正。日变数据的有效分离并分别改正可降低磁扰数据对地磁静日变改正的影响,提高日变改正质量。

4.3 处理结果对比

提取第9～10天地磁日变原始数据,分别利用5阶傅里叶级数分解、低通滤波和一维离散小波变换进行处理,比较处理结果。图17中,由于5阶傅里叶级数分解处理数据(黄线)不仅去除了高频的磁扰部分数据和低频的长期变化场部分数据,而且仅保留了24.0,12.0,8.0,6.0和4.8 h周期数据,所以只是保留了原始数据(黑线)的变化趋势,与原始数据实际误差较大。低通滤波和一维离散小波变换处理数据(蓝线、红线)均保留了低频信息,去除了高频信息,所以与原始数据高度吻合。在图17中红框处,原始数据变化速率大,低通滤波处理数据(蓝线)变化不明显,与原始数据(黑线)有较大误差,而一维离散小波变换处理数据(红线)更加吻合原始数据(黑线)。在图17中绿框内,低通滤波处理数据(蓝线)与原始数据(黑线)分离,误差变大,产生明显边界效应,而一维离散小波变换处理数据仍然与原始数据(黑线)高度吻合,未出现明显边界效应现象。

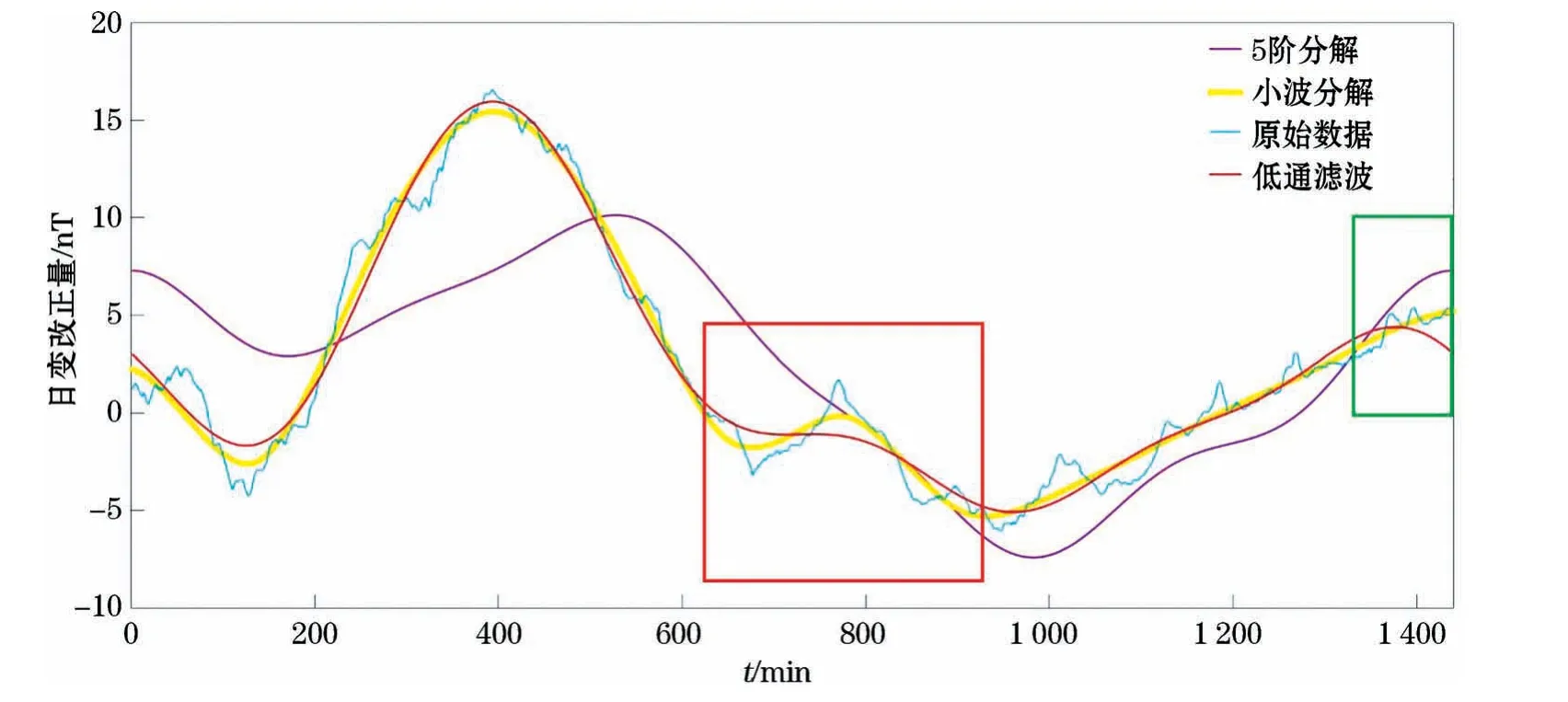
图17 处理数据对比Fig.17 Comparison of processing data

为进一步展示低通滤波和一维离散小波变换处理效果差异,分别将2种处理数据与原始数据做差,取差值平方作图18。低通滤波处理误差(蓝线)普遍高于一维离散小波变换处理误差(红线)。1400 min处,低通滤波处理误差(蓝线)逐渐增大,开始出现边界效应,而一维离散小波变换处理误差几乎为0,边界效应不明显。综上所述,一维离散小波变换比5阶傅里叶级数分解和低通滤波处理效果更佳,进一步验证了一维离散小波变换的科学性、准确性。

图18 误差对比Fig.18 Error comparison

5 结 论

本研究利用傅里叶变换和一维连续小波多尺度分析对地磁静日变原始数据进行分析,运用一维离散小波分解和单支重构对地磁静日变原始数据进行处理,对处理结果进行进一步分析和讨论,得到以下结论:

1)地磁静日变数据短期变化主要包括24,12和8 h周期变化,能量分布集中,其他频率能量分散;长期变化场对海洋地磁日变改正具有重要作用。

2)对地磁静日变数据进行一维离散小波分解与重构时,与其他基本正交小波相比,选用sym8小波作为基本正交小波处理效果较好,提取目标频段更精确、能量更集中、数据曲线更圆滑。

3)一维离散小波分解与重构技术可在不损害频段能量的条件下分离地磁静日变数据,且没有出现明显边界效应现象,保证了数据处理的保真度。

4)地磁静日变数据中包含的中小幅度的磁扰数据与短期变化场、长期变化场数据(地磁静日变改正数据)可利用一维离散小波变换在7尺度上进行有效分离,与之分别改正,可以降低磁扰部分数据对磁静日地磁日变改正的影响,提高日变改正质量。

对于小波变换,由于其选基灵活的特性,可根据不同数据、不同目的选用不同的小波基函数进行变换。选用不同小波基,变换效果也不尽相同。根据地磁日变数据特征和提取目标频段数据的处理要求,经过不同小波基试验,确定sym8小波作为一维离散小波分解与重构的基本小波,但sym8小波不一定是效果最好的基本小波。在以后的研究中,可能会构建更适合处理地磁日变数据的基本小波,研究小波变换在磁扰日期间日变改正中的应用,进一步提高小波变换技术应用水平和海洋地磁日变改正质量。

参考文献(References):

[1]National center of ocean standards and metrology.Specification for oceanographic survey:Part 8 Marine Geology and geophysics investigation:GB/T 12763.8—2007[S].Beijing:Standards Press of China,2007.国家海洋标准计量吣.海洋调查规范:第8部分 海洋地质地球物理调查:GB/T 12763.8—2007[S].北京:中国标准出版社,2007.

[2]BIAN G L,BIAN G,LIU Y C,et al.Study on the method of distinguishing geomagnetic quiet day from geomagnetic disturbed day marine in magnetic measurement[C]∥Chinese Survey and Mapping Society.Nineteenth Symposium on Hydrographic Survey and Charting.2007:33-37.卞光浪,边刚,刘雁春,等.海洋磁力测量中磁静日与磁扰日区分方法研究[C]∥中国测绘学.第19届海洋测绘综合性学术研讨会.2007:33-37.

[3]YANG Z.The study on diurnal variation correction mode of marine magnetic[D].Qingdao:Ocean University of China,2014.杨震.海洋磁力日变改正模式研究[D].青岛:中国海洋大学,2014.

[4]BIAN G,LIU Y C,ZHAI G J.A method to determine the correction datum of the geomagnetic diurnal variation[J].Hydrographic Surveying and Charting,2013,23(5):9-11.边刚,刘雁春,翟国君.一种确定地磁日变改正基值的方法[J].海洋测绘,2003,23(5):9-11.

[5]LI C M,LI J,YU Z,et al.The method of increasing precision of diurnal correction in high-precision magnetic survey[J].Computing Techniques for Geophysical and Geochemical Exploration,2004,26(3):211-214.李才明,李军,余舟,等.提高磁测日变改正精度的方法[J].物探化探计算技术,2004,26(3):211-214.

[6]XU W Y,KAMIDE Y.Decomposition of daily geomagnetic variations by using method of natural orthogonal component[J].Journal of Geophysical Research Atmospheres,2004,109(A5):124-136.

[7]YUAN G Y,ZHANG X M,WU Y Y,et al.Minimum point shift of the geomagnetic vertical component in diurnal variation and the internal-external equivalent current system S_q before the 2008 Wenchuan M_S8.0 earthquake[J].Earthquake,2015,35(3):102-112.袁桂平,张学民,吴迎燕,等.汶川8.0级地震前地磁低点位移与内外源S_q等效电流体系关系的研究[J].地震,2015,35(3):102-112.

[8]JANZHURA A S,TROSHICHEV O A.Determination of the running quiet daily geomagnetic variation[J].Journal of Atmospheric and Solar-Terrestrial Physics,2008,70(7):962-972.

[9]CHEN G,DU A M,ZHANG Y,et al.Kalman filter technique for defining solar regular geomagnetic variations[J].Progress in Geophysics,2017,32(5):1880-1885.陈果,杜爱民,张莹,等.利用卡尔曼滤波技术提取地磁规则日变化[J].地球物理学进展,2017,32(5):1880-1885.

[10]CUETO M,MCKNIGHT D,HERRAIZ M.Daily geomagnetic variations on the Iberian Peninsula[J].Geophysical Journal International,2018,152(1):113-123.

[11]XU X,ZHAO X D,W G X,et al.Analysis of data from the deep-sea geomagnetic observation buoy in the southwest subbasin of the South China Sea[J].Chinese Journal of Geophysics,2017,60(3):1179-1188.徐行,赵旭东,王功祥,等.南海西南次海盆深海地磁观测潜标的数据分析[J].地球物理学报,2017,60(3):1179-1188.

[12]ZHAO X D,DU A M,CHEN H R,et al.Inversion of the Sq current system and the geomagnetic diurnal variation model[J].Progress in Geophysics,2010,25(6):1959-1967.赵旭东,杜爱民,陈化然,等.Sq电流体系的反演与地磁日变模型的建立[J].地球物理学进展,2010,25(6):1959-1967.

[13]PENG F,ZHANG Q G,LUO S R.Application of harmonic analysis method applied diurnal correction of marine magnetic surveys[J].Hydrographic Surveying and Charting,2015,35(5):38-42.彭飞,张启国,罗深荣.调和分析方法在海洋磁力测量日变改正中的应用[J].海洋测绘,2015,35(5):38-42.

[14]YAMAZAKI Y,YUMOTO K,CARDINAL M G,et al.An empirical model of the quiet daily geomagnetic field variation[J].Journal of Geophysical Research Atmospheres,2011,116(10):352-353.

[15]LIU F,WU X P,XIAO F.The method realizing diurnal correction with harmonic model created by least square method in magnetically disturbed day[J].Journal of Geomatics Science and Technology,2016,33(6):582-587.刘帆,吴晓平,肖凡.磁扰日日变改正的最小二乘谐波建模实现方法[J].测绘科学技术学报,2016,33(6):582-587.

[16]LIU C,RUI X L,MIAO X F,et al.Research on anomalies characteristics of geomagnetic diurnal variation in Sichuan and adjacent areas[J].China Earthquake Engineering Journal,2020.http:∥kns.cnki.net/kcms/detail/62.1208.p.20200227.1404.006.html.何畅,芮雪莲,廖晓峰,等.四川及邻区地磁日变化异常特征研究[J].地震工程学报,2020.http:∥kns.cnki.net/kcms/detail/62.1208.p.20200227.1404.006.html.

[17]HESLOP D.A wavelet investigation of possible orbital influences on past geomagnetic field intensity[J].Geochemistry,Geophysics,Geosystems,2007,8.

[18]KLAUSNER V,PAPA A R R,MENDES O,et al.Characteristics of solar diurnal variations:a case study based on records from the ground magnetic station at Vassouras,Brazil[J].Journal of Atmospheric and Solar-Terrestrial Physics,2013,92:124-136.

[19]HARADA M,HATTORI K,ISEZAKI N.Signal discrimination of external geomagnetic effects using the transfer function approach with continuous wavelet transform[J].Handbook of Geophysical Exploration:Seismic Exploration,2010,40(10):243-258.

[20]HATTORI K,HAN P.Geomagnetic diurnal variations[U+3000]analysis in space and time associated with the 2011 off the Pacific coast of Tohoku earthquake(Mw9.0)[C]∥Egu General Assembly Conference.EGU General Assembly Conference Abstracts,2017.

[21]SID-ALI O,ALIOUANE L,ELADJ S.Multiscale analysis of geomagnetic data using the continuous wavelet transform:a case study from Hoggar(Algeria)[J].Seg Annual Meeting,2010(1):1222.

[22]LÓPEZ-MONTES R,PÉREZ-ENRÍQUEZ R,EDUARDO A.Fractal and wavelet analysis evaluation of the mid latitude ionospheric disturbances associated with major geomagnetic storms[J].Advances in Space Research,2015,55(2):586-596.

[23]YANG J P.An analysis of geomagnetic variations by wavelet entropy complexity[J].Progress in Geophysics,2010,25(5):1605-1611.杨建平.地磁场变化的小波熵复杂度分析方法[J].地球物理学进展,2010,25(5):1605-1611.

[24]MANDRIKOVA O V,SOLOVJEV I S,KHOMUTOV S Y,et al.Estimation of geomagnetic field disturbance using the wavelet transform[J].Pattern Recognition&Image Analysis,2016,26(4):773-781.

[25]LI Q,LIN Y F,ZENG X P.Wavelet analysis as a tool for revealing geomagnetic precursors of the Zhangbei earthquake[J].Chinese Journal of Geophysics,2006,49(3):751-760.李琪,林云芳,曾小苹.应用小波变换提取张北地震的震磁效应[J].地球物理学报,2006,49(3):855-863.

[26]LIU Q,BIAN G,YIN X D,et al.Adjustment of marine magnetic survey data with wavelet multi-scale analysis method[J].Hydrographic Surveying and Charting,2018,38(2):12-15.刘强,边刚,殷晓冬,等.基于小波分析的海洋磁力测量数据调差方法[J].海洋测绘,2018,38(2):12-15.

[27]LIN Z J,YANG L,WANG Q C.Applying wavelet transform in potential field data processing[J].Geophysical Prospecting for Petroleun,1997,36(3):70-78.李宗杰,杨林,王勤聪.二维小波变换在位场数据处理中的应用试验研究[J].石油物探,1997,36(3):70-78.

[28]VIDAKOVIC B,LOZOYA C B.On time-dependent wavelet denoising[J].IEEE Transactions on Signal Processing,1998,46(9):2549-2554.

[29]GUAN Z N.Geomagnetic field and magnetic exploration[M].Beijing:Geological Publishing House,2005:20.管志宁.地磁场与磁力勘探[M].北京:地质出版社,2005:20.

[30]XIA W,BIAN G,JIN S H,et al.Difference of geomagnetic diurnal variation between sea surface and ocean bottom and its effects on marine magnetic survey[J].Hydrographic Surveying and Charting,2015,35(1):7-10.夏伟,边刚,金绍华,等.海面与海底地磁日变化差异及其对海洋磁力测量的影响[J].海洋测绘,2015,35(1):7-10.