深空天线组阵的空间功率合成特性分析

张旭旺，王文灿，马文起，陈少卿，刘友永

（1.中国电子科技集团公司 第五十四研究所，石家庄 050081；2.96901部队，北京 100094）

引 言

20世纪中叶以来，航天技术的高速发展推动着人类不断向更遥远的深空开展探测活动[1-2]。随着探测距离的不断增加，地基深空测控系统与深空探测器之间的通信信号在巨大的路径损耗作用下将变得极其微弱。对此，主要的解决思路包括建造更大孔径的天线、开发更大功率的发射机以及天线组阵等。受天线重力下垂、热变形、风负荷增加以及加工精度等因素影响，当前的天线孔径几乎已经达到了极限。同时，过大的发射机功率面临着严重的散热问题，亦不利于地面工作人员的安全[3]。相对而言，通过多个小型天线组阵实现单个大孔径天线的功能具有成本低、易于操控、可扩展性强等优势，受到了各航天大国的高度关注[4-7]。

在深空天线组阵方面，国内外已有较多的相关研究[8-10]。张可等深入研究了相位误差对分布式地面站天线空间功率合成效率的影响[11]。孙克等通过分析多个误差源对天线组阵链路信号的影响，得出了大气相位扰动误差是造成天线组阵增益损失最主要因素的结论[12]。刘佳等提出了一种基于甚长基线干涉测量（Very Long Baseline Interferometry，VLBI）原理的上行组阵标校技术[13]。郭劲松等研究了天线组阵布局的约束条件以及对功率合成增益的影响[14-15]。赵卫东等提出了一种深空天线组阵宽带信号频域合成技术[16]。北京跟踪与通信技术研究所主持建立了我国首个天线组阵试验系统，在利用“嫦娥2号”卫星、欧洲航天局（European Space Agency，ESA）太空望远镜等深空目标进行的技术验证试验中，合成效率超过90%[17-19]。此外，徐茂格等归纳了我国在深空天线组阵方面的研究成果，并提出一些发展建议[20]。

国际上，美国一直是深空天线组阵技术的引领者，先后开发了全频谱处理阵列（Full Spectrum Processor Array，FSPA）、宽带阵列（Bread Board Array，BBA）以及下行阵列（Downlink Data Array，DDA）等下行天线组阵系统，并已开展了多次验证试验[21-26]。例如，2012年，利用FSPA系统合成了两个34 m天线接收的“火星科学实验室”（Mars Science Laboratory，MSL）探测器返回的多频频移键控（Multiple Frequency Shift Keying，MFSK）信号。2014年，在“新视野号”（New Horizons）穿越海王星轨道期间，利用DDA系统对戈尔德斯顿70 m天线接收的左右旋两路信号进行了合成。近年来，ESA也加大了深空天线组阵方面的研究，正筹划在现有35 m天线的基础上通过组阵方式将G/T值提高10 dB[27]。

针对深空天线组阵的空间功率合成特性，本文进行了深入的研究：①介绍了上行天线组阵和下行天线组阵的信号传输及信号合成模型；②分析了时延及相位补偿误差对天线组阵空间功率合成效率的影响；③分析了不同布阵形式下深空天线组阵的空间功率合成特性。

1 基本的信号模型

假定某深空天线组阵系统由K个天线组成，其中第k个天线的相心坐标为，k=1,2,···,K。同时，将深空探测器的坐标记作。于是，第k个天线到深空探测器的距离可以记作Lkp。

在上行天线组阵中，第k个天线发射的信号可以表示为

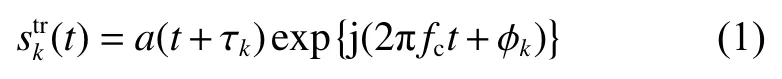
其中：a(t)为基带信号；τk为发射机对基带信号的时延补偿量；j为虚数单位；fc表示载波的频率；ϕk表示发射机对载波信号的相位补偿量，k=1,2,···,K。

于是，第k个天线所发射信号传播至深空探测器后，可以表示为

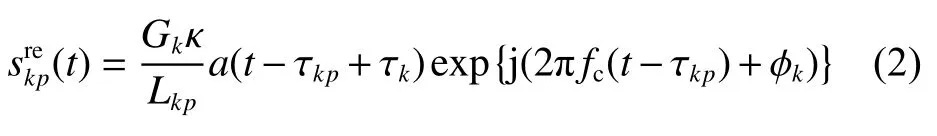
其中：Gk为第k个天线主波束方向的幅度增益（假定天线主波束方向指向深空探测器）；κ为常数；κ/Lkp表示信号随传播距离的衰减效应；τkp表示信号由第k个天线传播至深空探测器的时延。

显然，有τkp=Lkp/c，其中c表示光速。定义，其表示信号由第k个天线传播至深空探测器过程中的载波相移。这种情况下，深空探测器接收的信号经下变频至基带后可以表示为

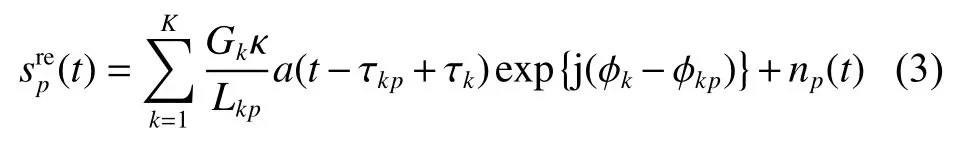
其中：np(t)表示深空探测器的接收机噪声。

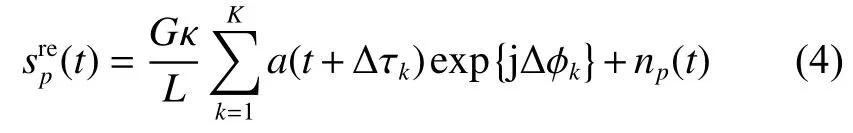
其中：∆τk=τk−τkp表示基带信号的时延补偿误差；∆ϕk=ϕk−ϕkp表示载波信号的相位补偿误差。

在下行天线组阵中，深空探测器发射的信号可以表示为

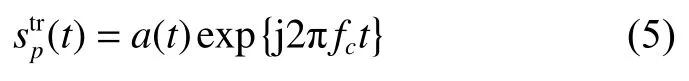
第k个天线接收的回波信号经下变频之后可以表示为

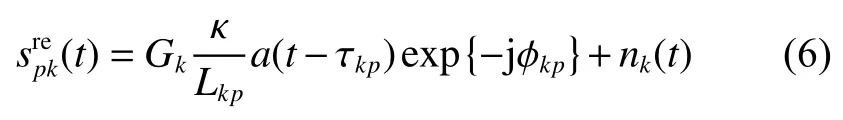
其中：nk(t)为第k个天线的接收机噪声，n1(t),n2(t),···,nK(t)相互独立且满足

对式（6）的信号补偿基带时延τk和载波相位ϕk，可得

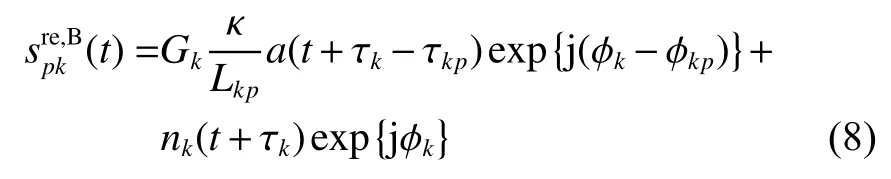
全部K个天线的接收信号经合成，可得

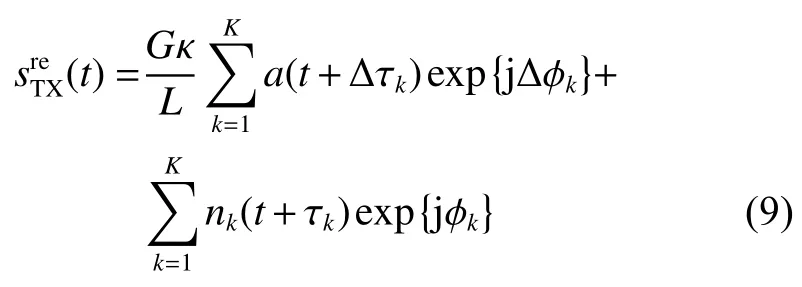
2 补偿误差对功率合成性能的影响

在完全补偿基带时延和载波相移的理想情况下，上行天线组阵和下行天线组阵分别可获得最大的K2倍和K倍信噪比增益。实际应用中，很难准确估计不同天线间的基带时延差异和载波相位差异，因而无法获得最优的信噪比增益。本节将分析基带时延补偿误差和载波相位补偿误差对上下行天线组阵的功率合成性能的影响，主要以信噪比增益损失为指标。

根据上行天线组阵和下行天线组阵的信号模型，当存在基带时延补偿误差∆τk和载波相位补偿误差∆ϕk时，系统获得的信噪比增益损失（相比于理想补偿情况）可以表示为

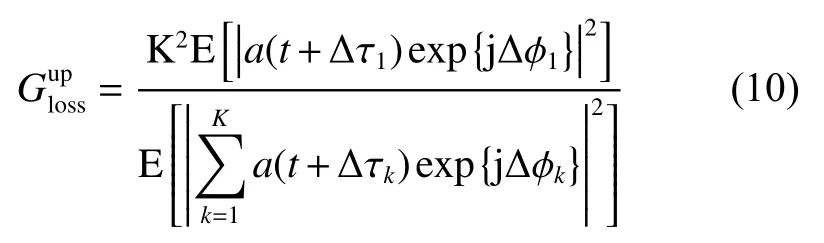
假定基带信号a(t)为由1 000个码片组成的伪码信号。各天线信号的基带时延补偿误差∆τk，k=1,2,···,K为零均值、标准差στ的高斯随机变量。同时，假定各天线信号的载波相位补偿误差∆ϕk，k=1,2,···,K为零均值、标准差σϕ的高斯随机变量。图1（a）和（b）分别示出了不同组阵天线数量对应的信噪比增益损失随基带时延补偿误差和载波相位补偿误差变化的情况。由图1（a）可以看出，给定K值时，信噪比增益损失会随着στ增大而逐渐增大；给定στ时，信噪比增益损失会随着K值增大而逐渐增大。由图1（b）可以看出，给定K值时，信噪比增益损失会随着σϕ增大而逐渐增大，直到σϕ增大到一定程度后，信噪比增益损失将不再变化。

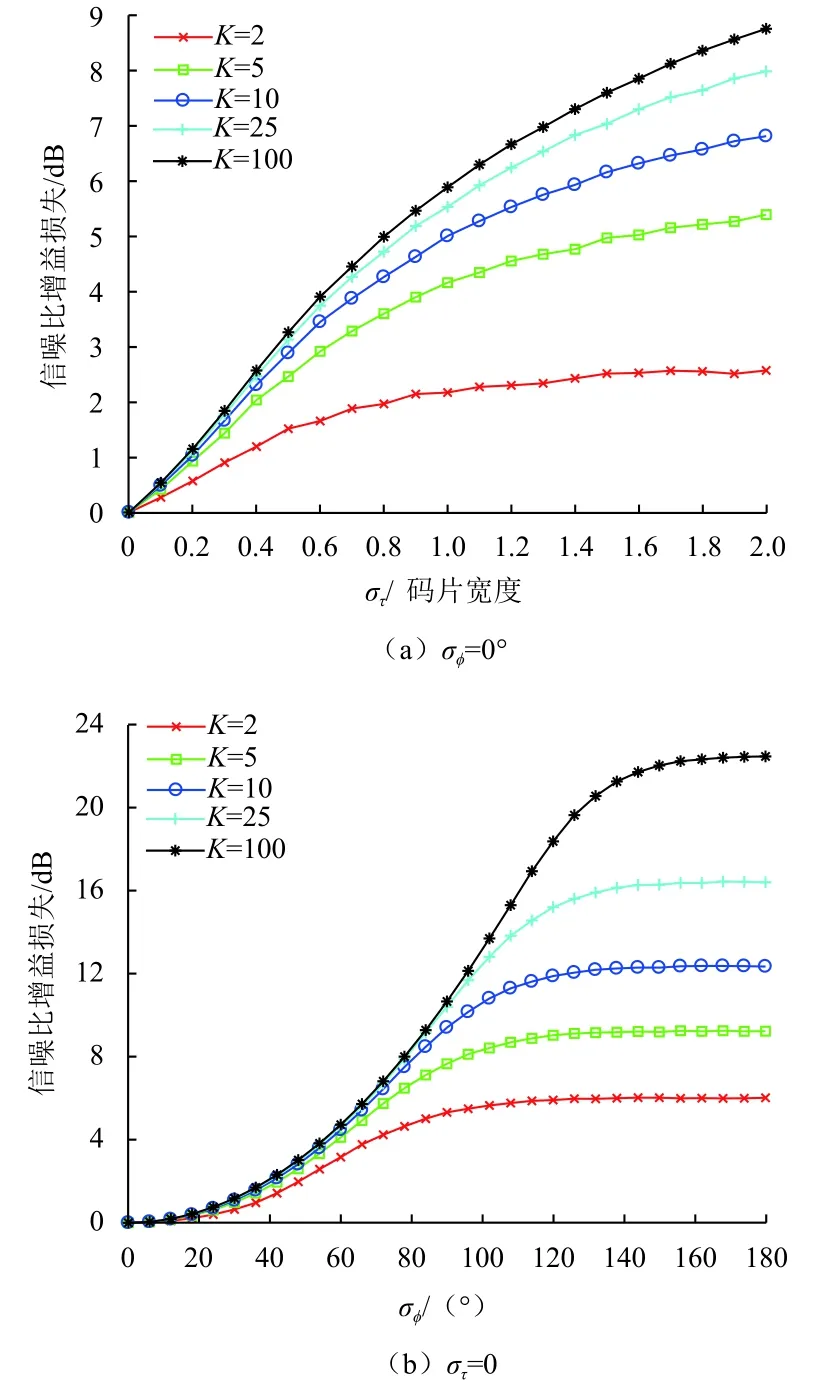
图1 信噪比增益损失随基带时延补偿误差和载波相位补偿误差变化的情况Fig.1 Loss of SNR gain varies with the compensation error of baseband time delay and the compensation error of carrier phase

图2示出了基带时延补偿误差和载波相位补偿误差都存在时信噪比增益损失变化的情况。其中，图2（a）中，στ=0.5；图2（b）中，στ=1；图2（c）中，στ=1.5。可以看出，当σϕ较小时，στ的影响占主导作用，信噪比增益损失与图1（a）中的对应点基本相同；当σϕ较大时，σϕ的影响占主导作用，信噪比增益损失只是略高于图1（b）中的στ=0情况。此外，当σϕ>140°时，信噪比增益损失将不再增加，并且不同στ对应的最大信噪比增益损失几乎相同。

3 天线阵型对功率合成特性的影响

在深空天线组阵系统中，每个天线的孔径可达数m甚至数10 m，再考虑到不同天线的空间间隔，可以确定各天线相心的间距将远超发射/接收信号的波长。此时，系统的空间功率合成方向图将会出现明显的栅瓣，栅瓣的数量、位置及幅度等特性与天线的阵型密切相关。

图2 信噪比增益损失随基带时延补偿误差和载波相位补偿误差变化的情况Fig.2 Loss of SNR gain varies with the compensation error of baseband time delay and the compensation error of carrier phase

3.1 理论分析

考虑如图3所示的抛物面天线，其中天线孔径记作D，焦距记作q。于是，根据文献[28]，该抛物面天线的远场方向图可以记作

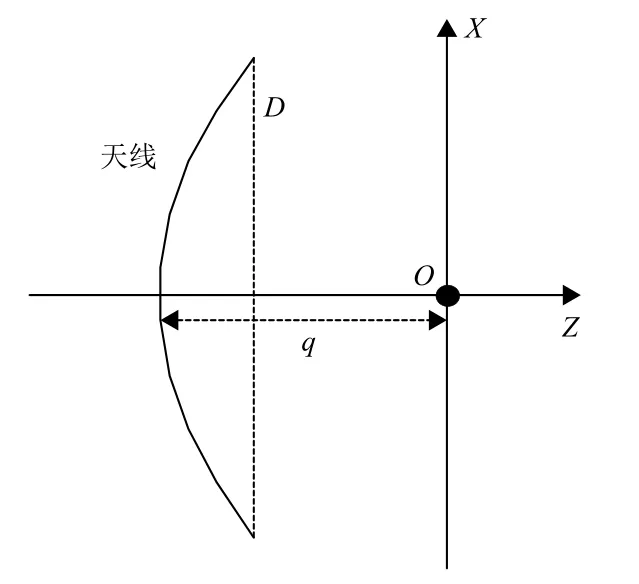
图3 抛物面天线示意图Fig.3 Schematic of parabolic antenna

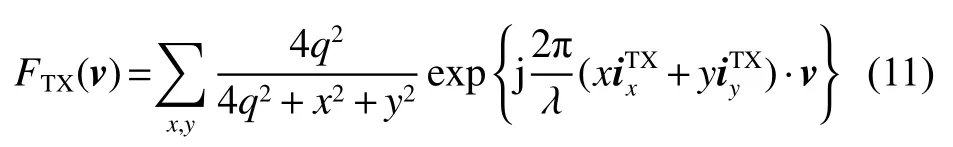
其中：x和y分别为z>0的x-y平面上孔径以内点的x和y坐标；满足，λ为载波波长，分别为图3所示直角坐标系（天线自身坐标系）沿X轴和Y轴方向的单位矢量，v为任意指定方向的单位矢量。

根据式（4）和式（9），K个天线进行组阵的阵列方向图可以直接记作

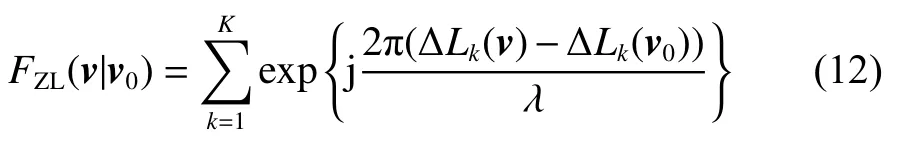
其中：v0和v分别为主波束方向和任意指定方向的单位矢量，∆Lk(v0)和∆Lk(v)分别为第k个天线沿v0和v方向的相对路径。

根据文献[28]，有

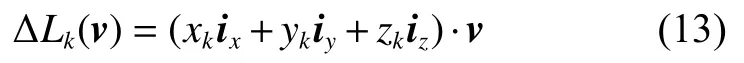
其中：(xk,yk,zk)T为第k个天线的相心在全局直角坐标系中的坐标；ix、iy和iz分别为全局直角坐标系沿X轴、Y轴和Z轴方向的单位矢量。

于是，K个天线进行组阵的合成方向图为天线方向图与阵列方向图的乘积，即

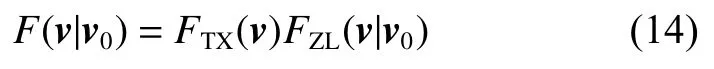
为了简便，假定K个天线排列成N行M列的二维均匀阵列，各天线相心均位于全局坐标系的XOY平面上，具体如图4所示，其中dx和dy分别为沿X轴和Y轴方向的阵列间距。同时，将单位矢量v和v0在全局坐标系中的坐标分别记作v=(xv,yv,zv)T和v0=(xv0,yv0,zv0)T。定义全局球坐标系与全局直角坐标系的转换关系如图5所示，其中α和θ分别为方位角和俯仰角。

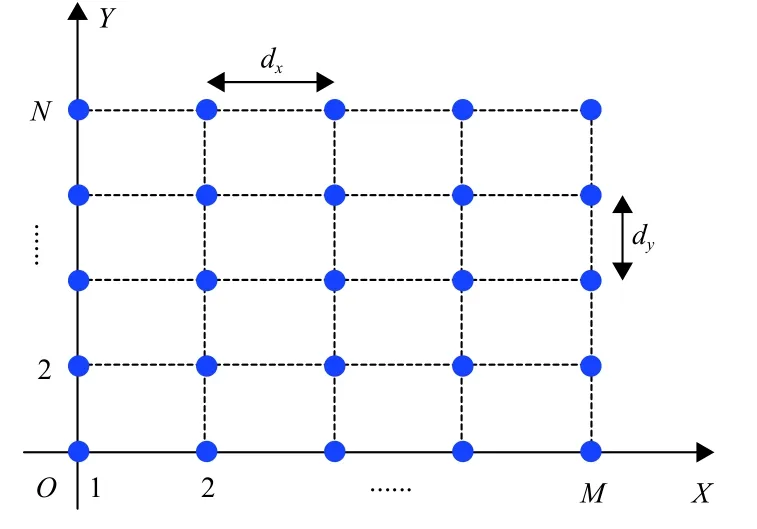
图4 二维均匀阵列布局图Fig.4 Layout of a two-dimensional uniformly distributed array

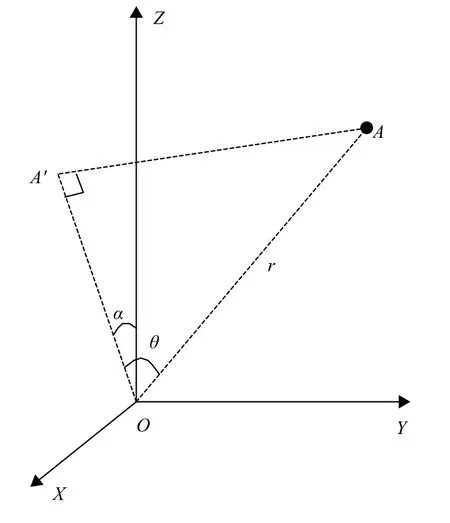
图5 球坐标系与直角坐标系之间的转换关系Fig.5 Transformation relationship between the spherical coordinate and the rectangular coordinate

这种情况下，有

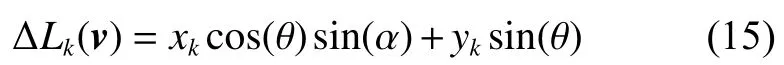
其中：α和θ分别为矢量v在全局球坐标系中的方位角和俯仰角。类似地，

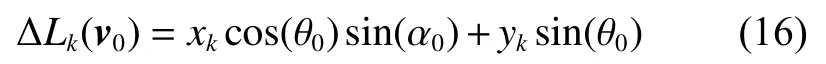
经整理后，阵列方向图可以记作

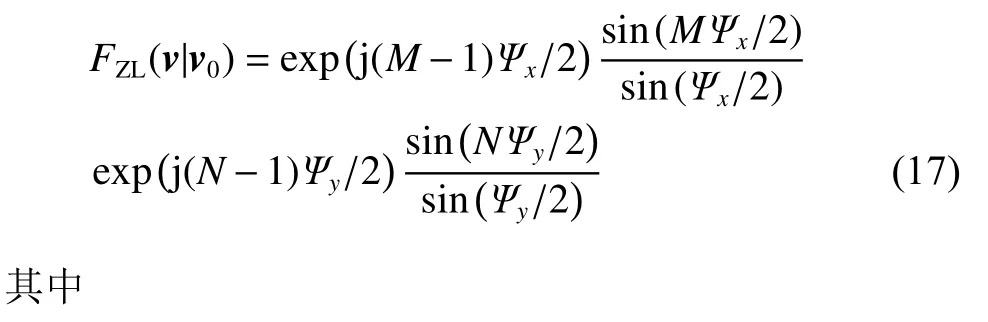
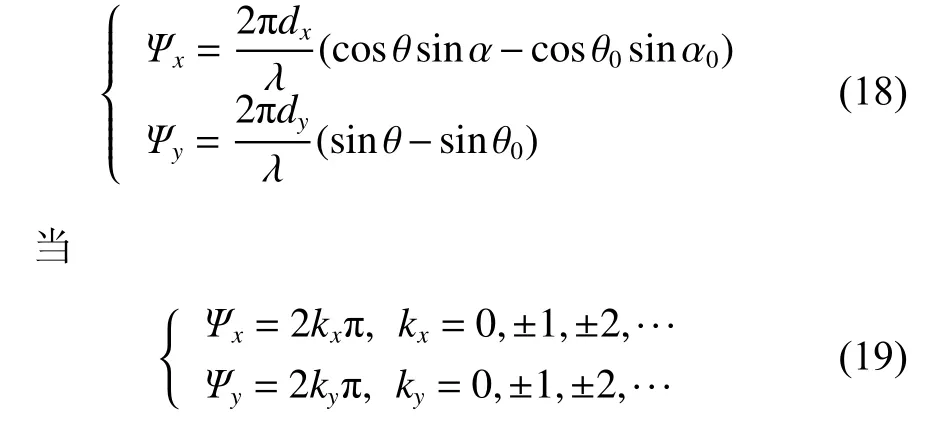
时，阵列方向图的幅度|FZL(v|v0)|取到了极大值。此时，对应的(α,θ)称作阵列方向图的主瓣（kx=ky=0）或栅瓣位置（kx或ky不为零）。当α0=θ0=0°时，部分典型栅瓣位置为

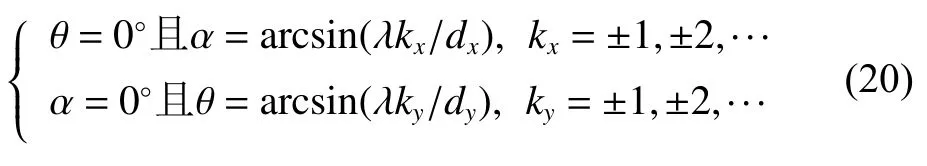
由于抛物面天线的方向图不存在栅瓣且其主瓣宽度显著大于阵列方向图的主瓣宽度，所以当抛物面天线的中轴指向主波束方向时，式（19）和式（20）所确定的(α,θ)就可以近似视为合成方向图的栅瓣位置。

3.2 仿真分析

图6为某个均匀分布方形天线组阵的方向图，其中，主波束方向以及抛物面天线的中轴均指向正上方，fc=3.2 G H z，D=16m，q=5 m，M=4，N=4，dx=32 m，dy=32 m。图6（a）为抛物面天线的方向图，方位维和俯仰维的3 dB波束宽度均为0.36°。图6（b）为阵列方向图，可以看出栅瓣分布规律且幅度与主瓣接近。图6（c）为合成后的总方向图，可以看出天线方向图的主瓣很好地抑制了阵列方向图的栅瓣，最终仅在天线方向图主波束内残留了几个较高的栅瓣。表1列出了部分典型栅瓣的位置，其中仿真确定的栅瓣位置与式（20）预测的栅瓣位置基本一致。

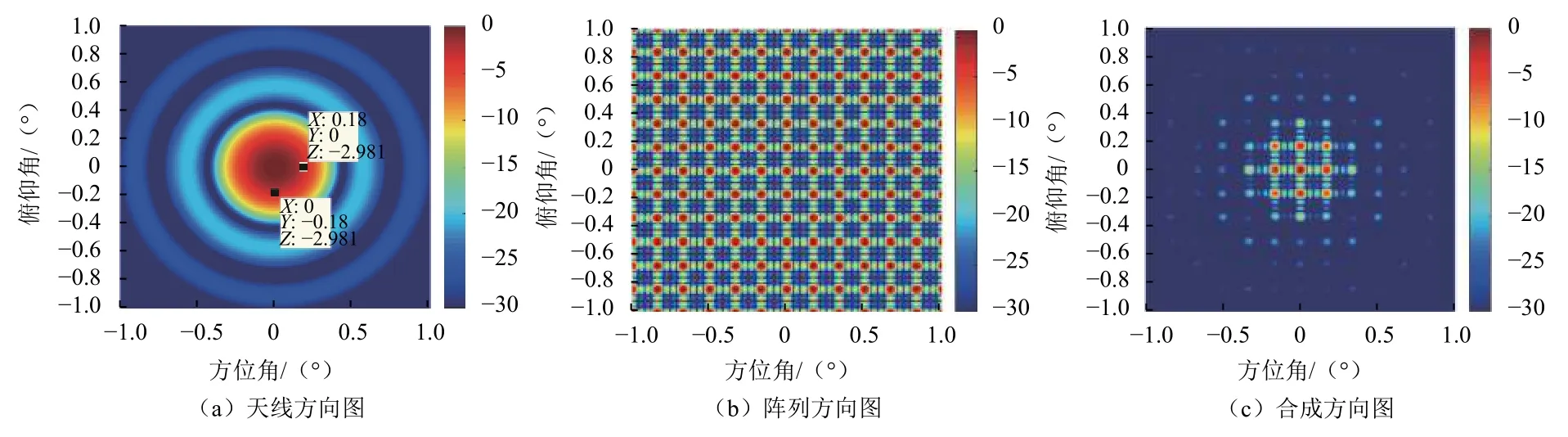
图6 均匀分布天线组阵的方向图Fig.6 Pattern of a uniformly distributed antenna array

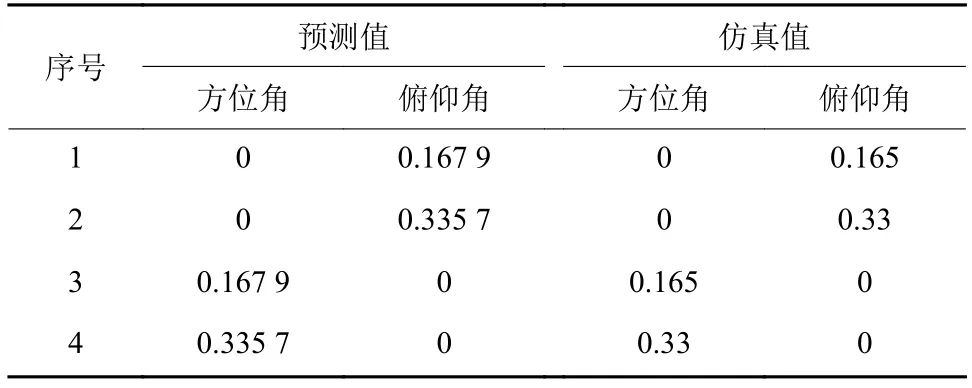
表1 均匀分布天线组阵部分栅瓣的位置Table 1 Position of some gate valves of uniformly distributed antenna array（°）

在均匀分布方形天线组阵的基础上，进一步考虑非均匀分布天线组阵的栅瓣特征。具体而言，在前述均匀分布方形天线组阵的基础上，将每个天线相心的X坐标和Y坐标分别增加一个在[−∆x,∆x]和[−∆y,∆y]范围内均匀分布的随机变量。通过调节∆x和∆y的取值，调整天线组阵的非均匀分布程度。

图7示出了∆x=∆y=4 m和∆x=∆y=8 m情况下非均匀天线组阵的合成方向图。可以看出，随着∆x和∆y取值的增加，天线组阵的非均匀分布程度逐渐增加，栅瓣的分布逐渐变得不规则，且周围出现了更多的不规则小亮斑。

为了更深入地分析天线阵型对合成方向图中主瓣和栅瓣的影响，接下来分析圆形天线阵和L形天线阵的情况。图8（a）示出了圆形天线阵的天线分布图。其中，在中心处有1个天线；在内层的小圆圈上共有5个天线均匀分布，间隔72°；在外层的大圆圈上共有10个天线均匀分布，间隔36°。图8（b）示出了该圆形天线阵的合成方向图。可以看出，主瓣非常规则，且波束宽度略大于图6（c）所示均匀方阵的波束宽度；栅瓣分布变得很不规则，且幅度显著低于主瓣。

图9（a）示出了L形天线阵的天线分布图，其中各天线的间距为32 m。图9（b）示出了该L形天线阵的合成方向图。可以看出，主瓣不再是规则的圆形，而是斜着放置的椭圆形；栅瓣的分布与均匀方阵的栅瓣分布基本一致，只是栅瓣的形状也变成了椭圆形。

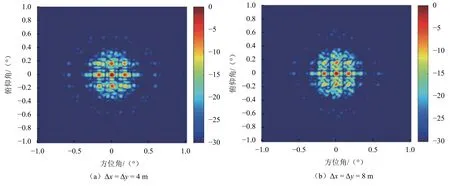
图7 非均匀分布天线组阵的合成方向图Fig.7 Synthesis pattern of a non-uniformly distributed antenna array

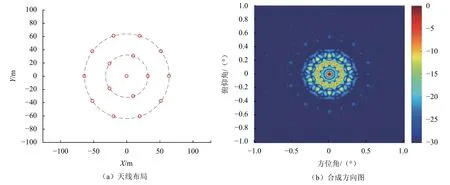
图8 圆形天线组阵的方向图Fig.8 Pattern of a circular antenna array

图9 L形天线组阵的方向图Fig.9 Pattern of a L-shaped antenna array

4 结 论

本文深入研究了深空天线组阵的空间功率合成特性。基于信号合成模型，分析了基带时延和载波相位补偿误差对深空天线组阵空间功率合成性能的影响。此外，还进一步研究了天线阵型对深空天线组阵栅瓣位置及幅度的影响。仿真结果表明，均匀分布方形天线组阵的栅瓣分布均匀且幅度较大，随着天线组阵非均匀分布程度的增加，栅瓣会变得散乱分布且幅度降低，但主瓣的变化并不明显。圆形天线组阵的栅瓣分布比较散乱，而L形天线组阵的主瓣和栅瓣均为椭圆形。本文的研究为深空天线组阵系统的设计提供了一定的参考。