力法基本结构的选择技巧
2020-11-12赵朝前
赵朝前
(四川建筑职业技术学院土木工程系,四川 德阳 618000)
1 问题的提出
力法是计算超静定结构最基本的方法[1],在力法的计算过程中关于系数和自由项的计算都是在选取的基本结构上进行的。力法的基本结构是将超静定结构的多余约束去掉后得到的静定结构[2],对同一个超静定结构可以采取不同的形式去掉其多余约束,亦即可以选择不同的基本结构来求解,以不同的基本结构为基础进行计算的难易程度不同,因此力法求解超静定结构的关键在于基本结构的选择[3]。 为了使得求解过程较为容易,应该选择合理的基本结构,所谓合理的基本结构是指能使力法典型方程更为简便,包括方便计算系数和自由项以及避免求解联立方程。本文主要讨论怎样选择超静定梁和超静定刚架的基本结构可以使系数和自由项的计算变得更容易。
2 合理的力法基本结构
对于超静梁和刚架,计算力法典型方程中的系数和自由项步骤是先分别画出图和Mp图,然后采用图乘法进行计算。 为了便于画出图和Mp图并避免要进行图形分割才能图乘,本文提出采用铰化法来选择合理的基本结构。
所谓铰化法是指将原结构中的固定端改成固定铰,将刚结点改成铰结点,这样就可将原超静定结构的基本结构确定为由若干根简支梁所组成的静定结构,如此就能由较为熟悉的简支梁的弯矩图方便地画出图和Mp图,同时也能避免图乘要进行图形分割。
以用力法求解图1 所示的连续梁为例说明铰化法选择基本结构的优势。

图1 连续梁
此连续梁为三次超静定结构,力法典型方程为:

式中X1,X2,X3为多余未知力。
主系数δii和副系数δij、自由项Δip分别由(2)、(3)式计算。
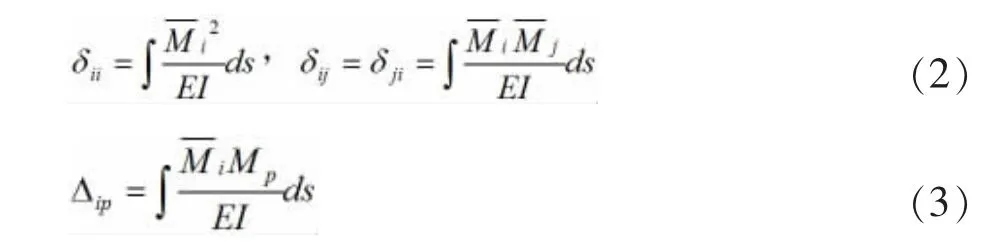
解出多余未知力后,原超静定结构的弯矩由(4)式计算:为基本结构在

图2 选择悬臂梁为基本结构,图3 则以用铰化法选择由3 根简支梁组成的基本结构。
通过比较可以发现,如果采用一般的常规方法即以悬臂梁作为基本结构,虽然图比较简单,但Mp图比较复杂,同时在用图乘法计算系数和自由项必须要进行图形分解,计算较为烦琐也容易出错。
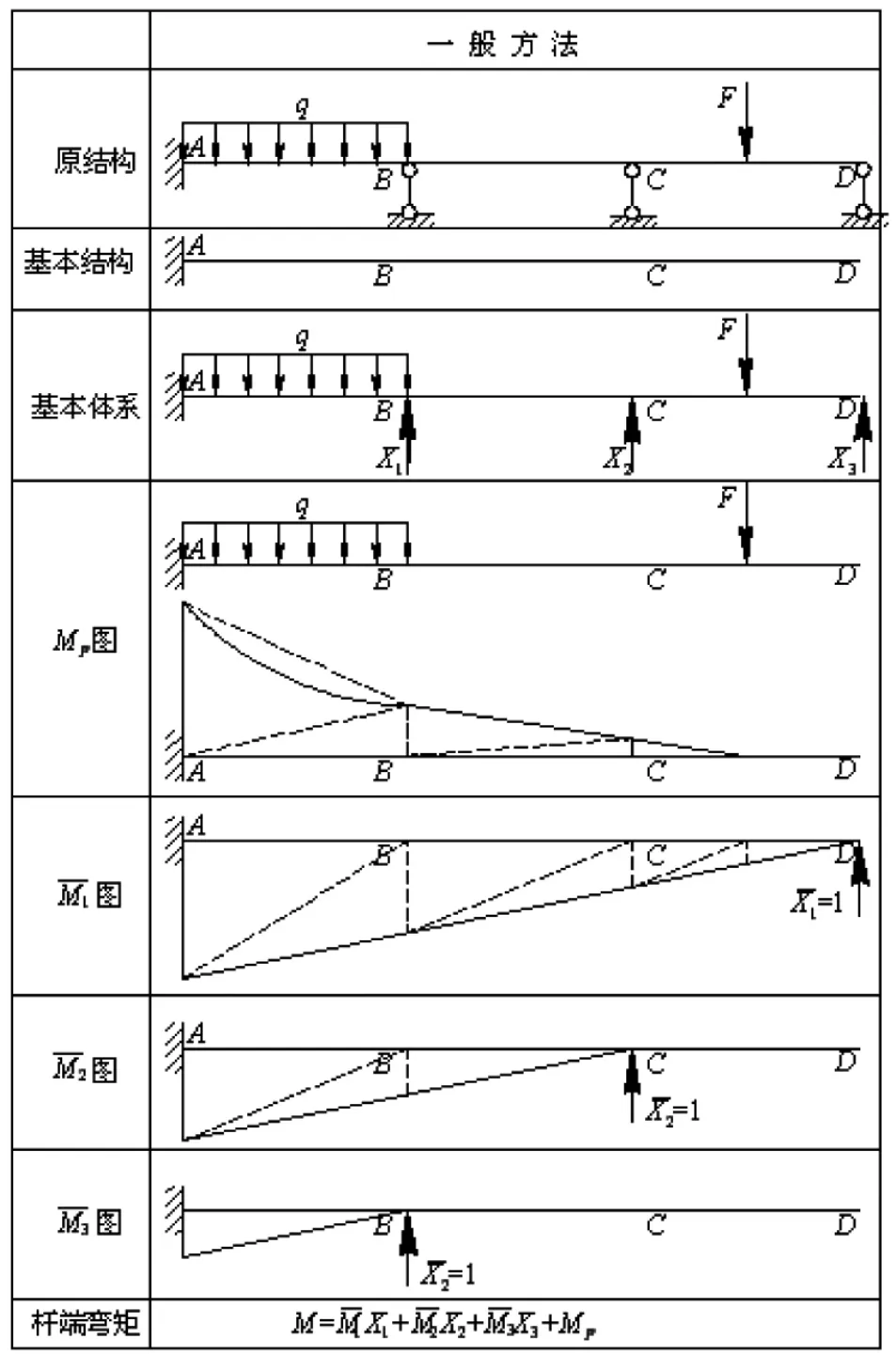
图2 以悬臂梁为基本结构计算过程
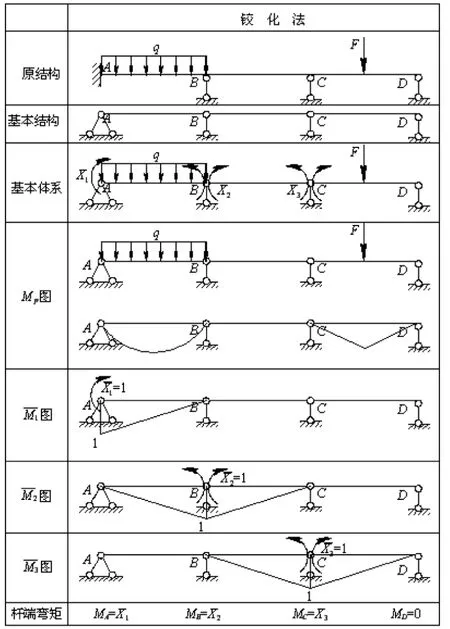
图3 以铰化法选择基本结构计算过程
3 应用举例
计算图4 所示连续梁并画出M 图。
以铰化法选择由两个简支梁构成的基本结构,列出力法典型方程:
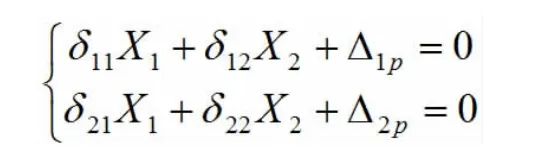

图4 铰化法计算连续梁
对于图5 所示超静定刚架也适合用铰化法选择其基本结构。

图5 铰化法计算超静定刚架
4 结论
通过铰化刚结点和固定端来选择力法的基本结构,(1)可以使图和Mp图都是简支梁在单一荷载作用下的弯矩图,非常容易画出;(2)图和Mp图都是简单规则形状的图形,用图乘法计算系数和自由项时不需要进行图形分解即可直接图乘,易于计算;(3)在多余未知力Xi截面处,只有图中该截面弯矩等于1, 而其余的图和Mp图中该截面的弯矩都等于0,因此原超静定结构杆端截面的弯矩正好等于相应的多余未知力,很方便最终弯矩图的绘制。 显然采用此种方法可以使计算过程简单方便,这种方法可以求解所有的连续梁和没有结点线位移的超静定刚架。
