基于自适应微簇的任意形状概念漂移数据流聚类
2020-11-12韦洁华
韦 洁 华
(广州南洋理工职业学院通识教育学院 广东 广州 510925)
0 引 言
随着移动互联网的应用和普及,视频流、多媒体流,以及各类实时消息流成为了网络数据的一个重要组成部分,对这些实时数据流进行快速、及时地挖掘和分析是当前大数据研究领域的一个重要诉求[1]。数据流聚类是数据挖掘的一个重要预处理步骤,能够提高后续数据流挖掘分析的效率和效果[2]。由于数据流聚类对效率和准确率均具有极高的要求,所以近期热门的深度学习技术难以适用于该情况,而机器学习成为数据流聚类领域的重要技术[3]。在机器学习技术中,神经网络具有误差小、动态性好的优点,但收敛速度慢[4];决策树分类的速度快、准确率高且对高维数据性能较好,但对于不平衡数据流性能较弱,且极易过拟合[5];支持向量机(Support Vector Machine, SVM)对二分类问题的处理速度快、准确性好,但对大规模样本的训练速度很慢,对多分类问题的效果也较差[6]。
最优路径森林(Optimum Path Forest, OPF)[7]是新出现的一种监督学习方法,该方法将训练集建模为完全图,以训练样本为节点,以节点间距离为弧,基于完全图生成最优路径树,每棵树为一个类别。分类程序计算样本和树的距离,将样本分类为距离最近的类别树。OPF不依赖任何参数,且在训练阶段无须参数优化处理,因此其训练和分类均十分快速[8]。OPF的分类精度与SVM接近,且优于决策树、贝叶斯分类器等经典的机器学习方法,而其训练速度和分类速度明显快于SVM,也无须假设簇的形状。OPF目前已经被研究人员运用到许多应用领域中,如大数据监督聚类问题[9]、人脸表情识别[10]和协同过滤推荐系统[11]等,并且取得了一定的性能优势。
在数据流的聚类方案中,基于密度的聚类算法是一个重要的分支,此类算法支持任意形状的簇。在早期的动态数据流聚类算法[12-13]中,大多采用迭代程序或者分治思想对数据流进行聚类处理,此类算法只能对数据流进行概括,无法反映数据流的动态。Clustream[14]是解决数据流聚类问题的一个经典框架,该框架在线地对数据流进行初级聚类,并保存初级聚类的结果,然后在离线阶段由用户设定数据流的处理措施。Clustream能够描述数据流的动态变化,具有较好的可扩展性,许多研究人员对Clustream框架进行了扩展,例如:双层网格和Clustream结合[15],二重k近邻和Clustream结合[16]。但上述数据流聚类算法均为在线和离线混合的处理框架,并且需要用户输入一些固定的参数,如数据流维度、微簇半径等,这些参数在实际应用中难以确定,如果取值出现偏差,会导致系统性能产生较大的衰减。
本文设计一种基于自适应微簇的任意形状概念漂移数据流聚类(Data Stream Clustering based on Adaptive Micro-Clusters, DSCAMC),该算法支持任意形状的数据流,并且无须预设相关参数,是一种完全在线的数据流聚类算法。本文的贡献主要有:(1) 开发递归微簇半径寻优机制,自适应地搜索微簇半径的局部最优值。(2) 开发缓存机制保留目前暂不相关的微簇,而这些微簇在未来可能存在相关性,缓存机制有助于加快数据流的处理。(3) 采用最优路径森林结构组织数据流宏簇的完全图,通过最优路径将新到达的数据分类。借鉴重引力搜索算法的引力机制,提出微簇的能量函数,该函数评估微簇的空间密集程度,数据点越靠近微簇中心,对能量的贡献越大。然后将能量最大的微簇作为最优路径树的根节点,即代表性节点(原型)。
1 数据流的概念漂移问题
如果一个目标概念随着时间变化,此时发生概念漂移。设两个目标概念为A和B,数据流为I={i1,i2,…,in}。假设在数据id之前,目标概念固定为A,在数据id+1和id+Δx之间发生概念漂移,目标概念A变为概念B,其中,Δx为概念漂移的速率。在线的概念漂移分类器在收到一个数据实例之后,将数据流分批,处理数据流批的方法主要有三种类型:完全内存方法、完全不保存方法和固定窗口方法。本文方法属于完全不保存和极少量缓存相结合的方法。
2 最优路径森林分类器
最优路径森林(Optimum Path Forest, OPF)分类器包括一个监督学习程序和一个无监督学习程序,监督学习程序主要有完全图方法和k-NN图方法,k-NN图方法需要用户输入kmax参数,该参数受实际应用的影响较大,所以本文采用完全图方法。考虑完全图的OPF模型,设Z=Z1∪Z2为一个标记数据集,其中Z2和Z2分别为训练集和测试集。设λ(s)函数为样本s∈Z1∪Z2分配正确的标签,表示为λ(s)∈{1,2,…,c},s∈Rn。设S∈Z1为代表性样本集(原型样本集),d(s,t)为样本s和t间的距离。聚类问题可描述为基于S、d和Z1构建最优分类器,该分类器可预测样本s∈Z2的标签λ(s)。
OPF分类器构建一个完全图,每个节点为一个微簇,同一个类别的微簇组成一棵最优路径树(宏簇)。文中微簇为球形,但是宏簇为任意形状。完全图中每条路径都有一个代价值,计算从原型到每个样本的最小代价路径,每处理完一个样本,该样本则获得一个标签和最小代价值。
设(Z1,A)为一个完全图,其中每个节点是Z1的一个微簇,A为边的集合,每条边具有一个权值。Z1的每个路径表示为一组节点的序列π=
代价函数fmax定义为:
fmax(π·
(1)
式中:fmax(π)为π中相邻样本间的最大距离。
OPF包括训练阶段和分类阶段,训练程序基于fmax和S建立最优路径森林,分类程序将测试样本分类。训练阶段搜索所有样本s∈Z1的最优路径P*(s),建立最优路径森林P。设R(s)∈S为P*(s)的根节点,OPF计算P*(s)每个s的代价C(s),设s的标签为L(s)=λ(R(s)),s的前继节点为P(s)。分类阶段将测试样本t∈Z2和最优路径森林连接,寻找代价最小的树,代价最小的计算方法为:
C(t)=min{max{C(p),d(p,t)}} ∀p∈Z1
(2)
式中:节点p∈Z1为最小化C(t)的节点。图1和图2分别为OPF训练和测试的实例。
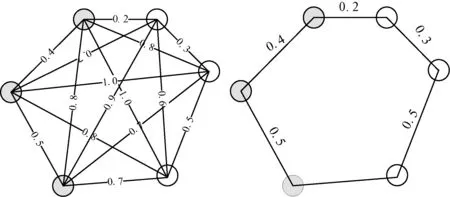
(a) 数据流的完全图表示 (b) 最小生成树

(c) 设定原型样本 (d) 两棵最优路径树图1 最优路径树的训练程序例子
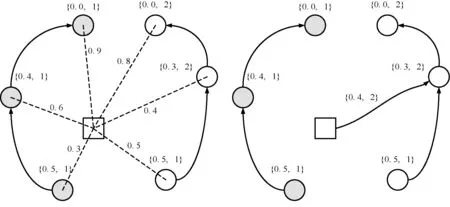
(a) 测试样本和所有节点连接 (b) 选择其中的最优路径图2 最优路径树的测试程序例子
3 数据流在线分类器
DSCAMC的目标是提高数据流的聚类质量,降低存储成本和时间成本,并且具备概念漂移的能力。
3.1 数据结构设计
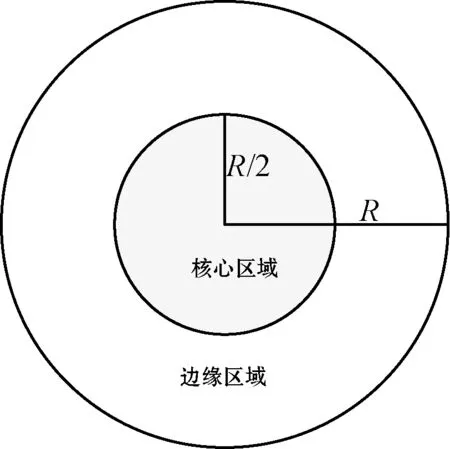
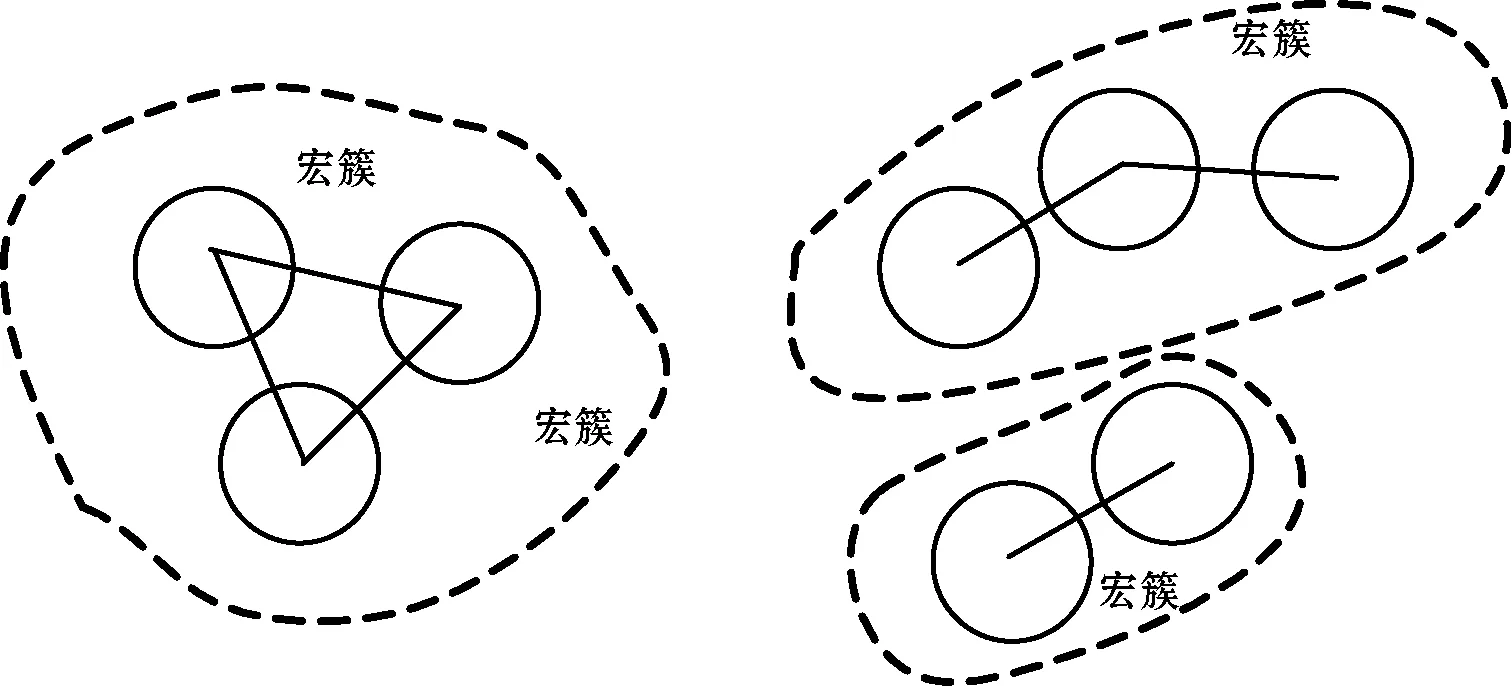
DSCAMC基于密度实现聚类处理,首先将聚类信息概括为微簇的形式,根据分簇图内微簇间的隶属度将微簇连接成宏簇。DSCAMC定义一个衰减参数来处理数据流的进化特性,定义一个最小密度阈值来区分微簇和孤立点。衰减参数定义为在给定时间区间到达的数据点总数量,微簇的最少数据点数量定义为Thden。图3(a)和图3(b)分别为一个微簇的结构和重叠微簇的示意图,从图3(b)推理出图3(c)的分簇图。
(a) 微簇的结构

(b) 重叠的微簇
(c) 分簇的图图3 基于密度的微簇结构示意图
设微簇为MC,表示为元组形式:MC(N,N′,C,R,E,EL,M),其中:C为微簇的中心,定义了微簇在数据空间的位置;R为微簇的半径,定义了微簇的空间范围,R/2以内的区域称为核心区域,R/2~R半径的区域称为边缘区域;N为微簇的局部密度,定义为微簇内的数据点数量;N′定义为微簇边缘区域内的数据点数量;E为微簇的能量,每次数据点分簇之后均需要更新微簇的能量值E,能量值小于等于0的微簇从分簇图中删除;EL为微簇的连接列表,如果一个微簇的核心区域和另一个微簇的核心区域或者边缘区域重叠,则认为这两个微簇之间连接;M为该微簇所属的宏簇,宏簇由若干个连接的微簇组成。
本文算法共维护4种类型的微簇,分别为核心微簇、潜在微簇、弱微簇和孤立微簇,根据微簇的密度阈值Thden和能量值E区分4种微簇类型。
定义1将核心微簇记为MCcore(N,N′,C,R,E,EL,M),核心微簇应满足以下条件:N≥Thden;N′≤N;Rmin≤R≤Rmax;E>0。
定义2将弱微簇记为MCwea(N,N′,C,R,E,EL,M),核心微簇应满足以下条件:Thden≤N;N′≤N。
定义3将潜在微簇记为MCpot(N,N′,C,R,E,EL,M),潜在微簇应满足以下条件:N≤Thden;N′≤N。
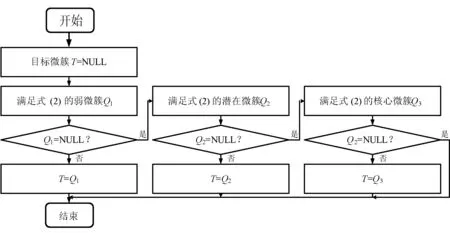
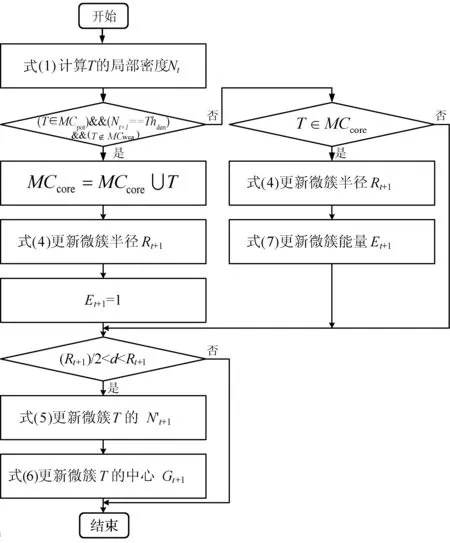
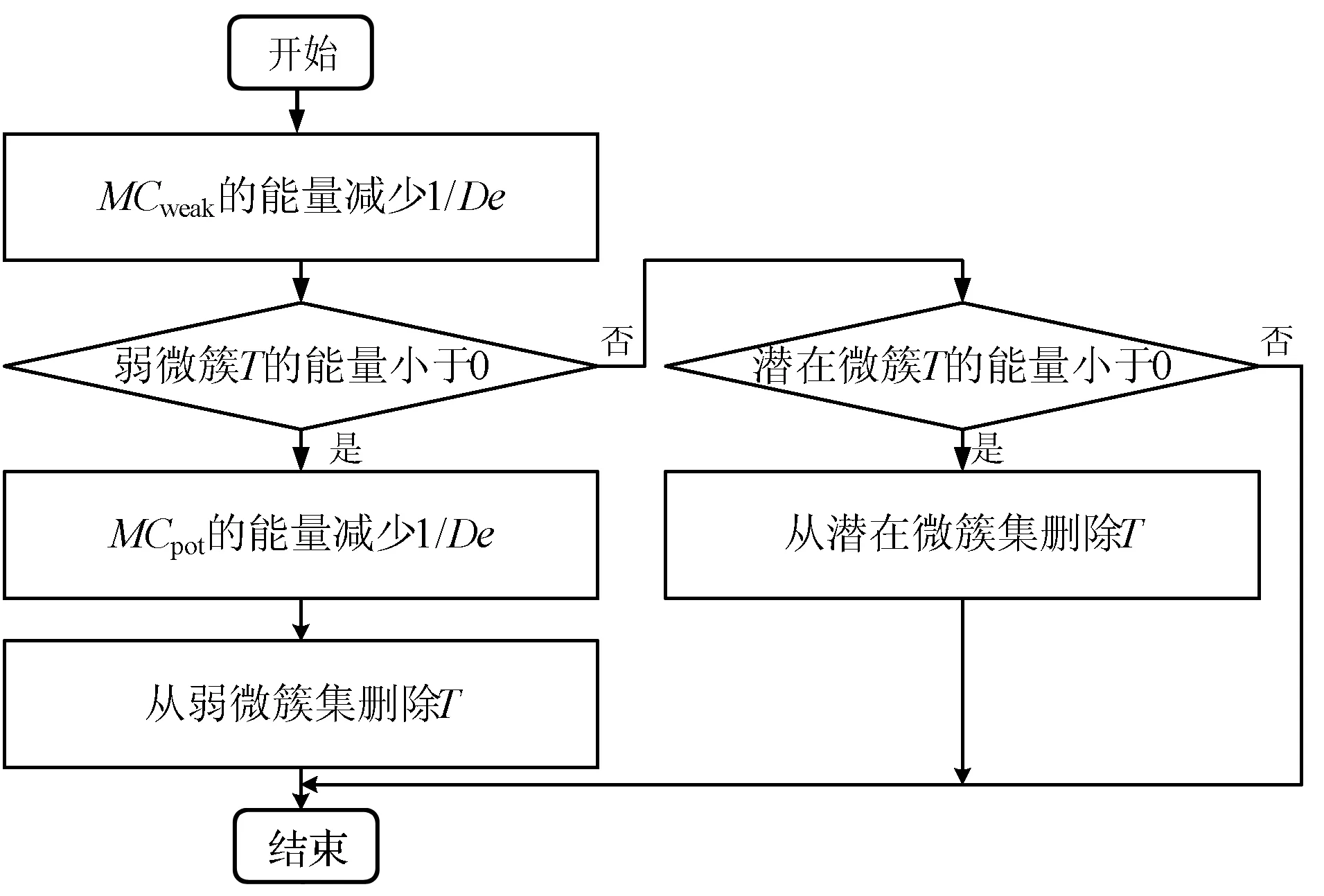
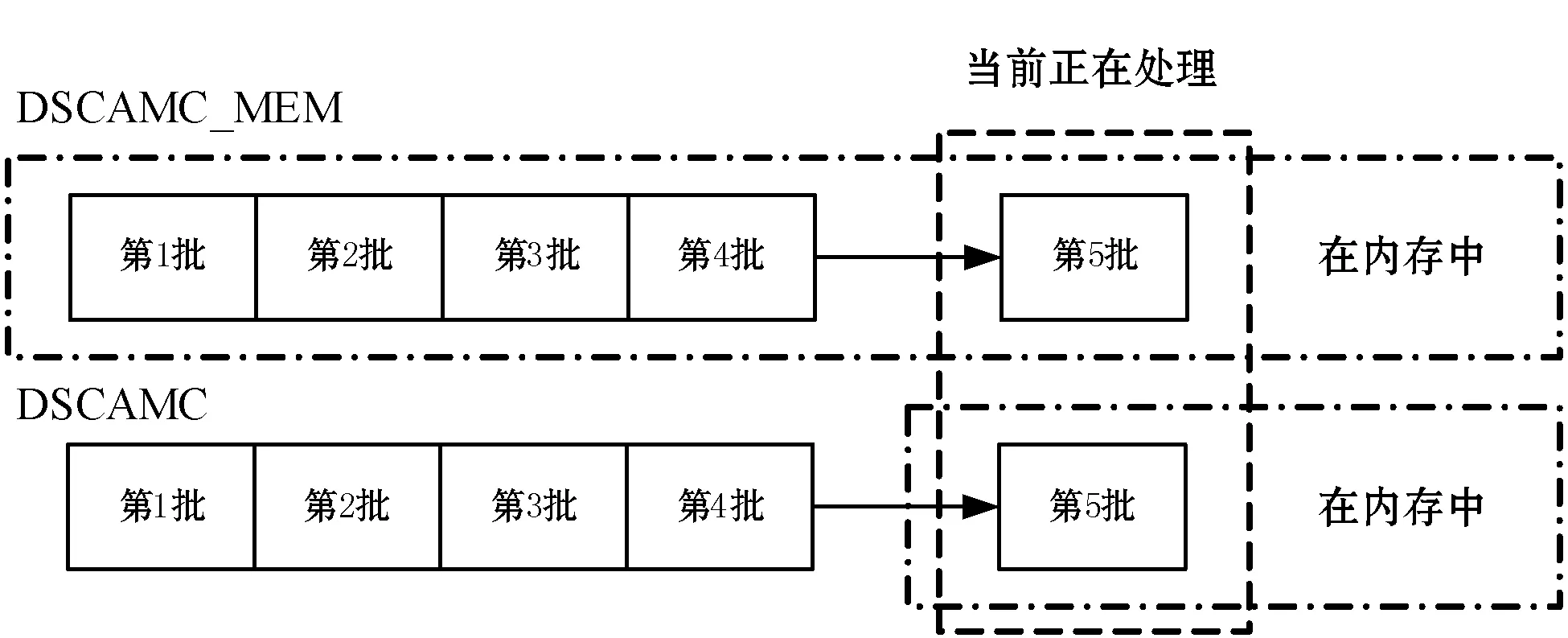
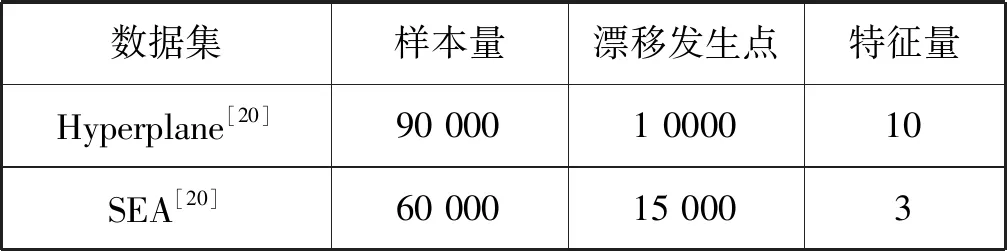
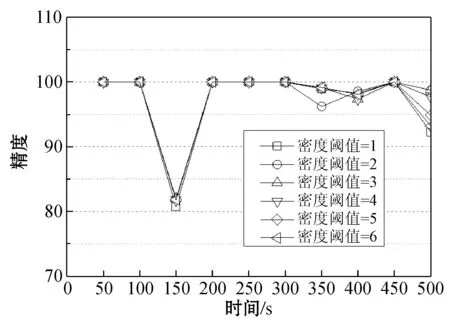
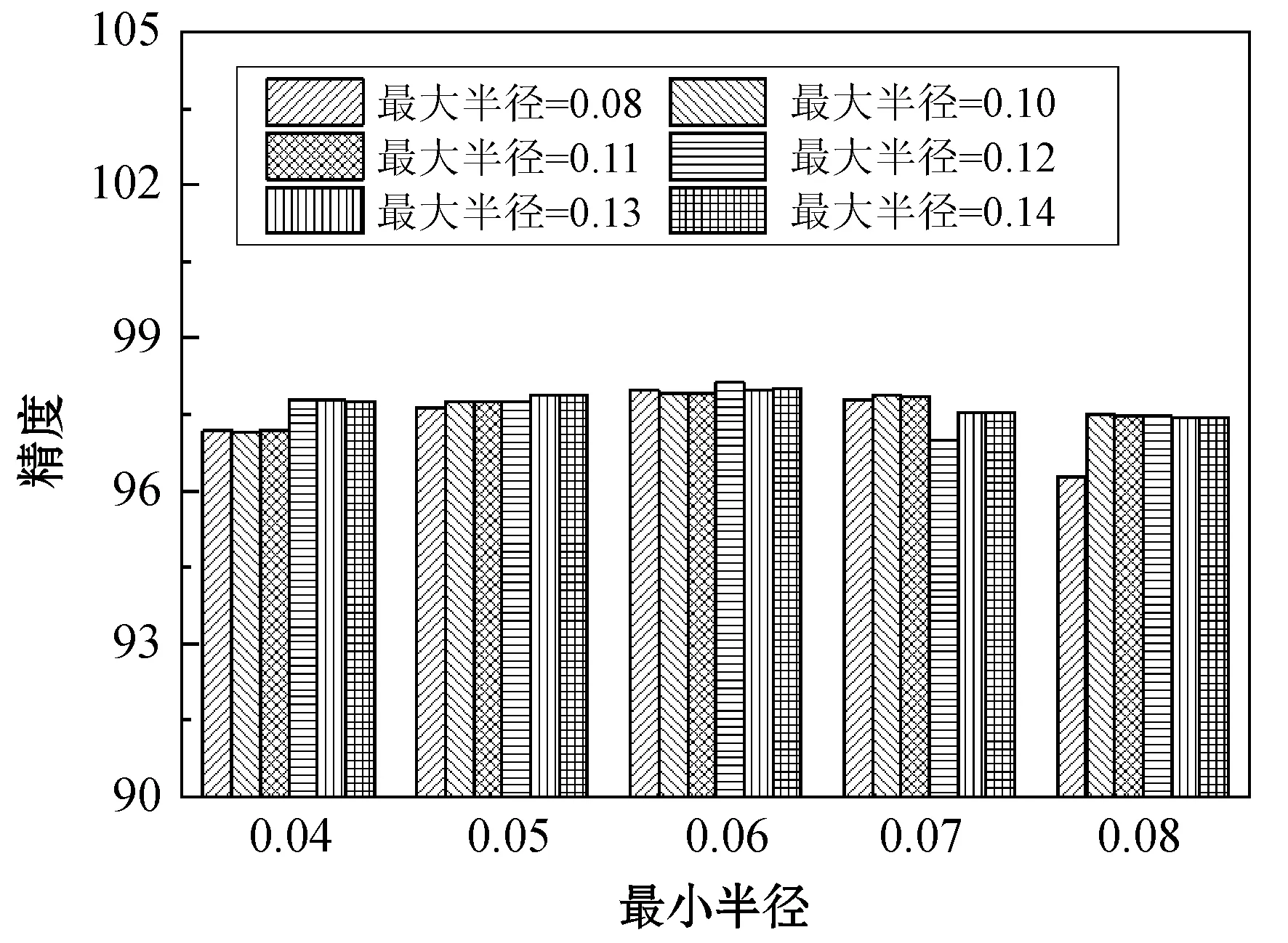
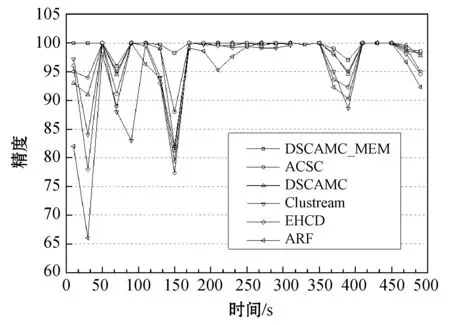
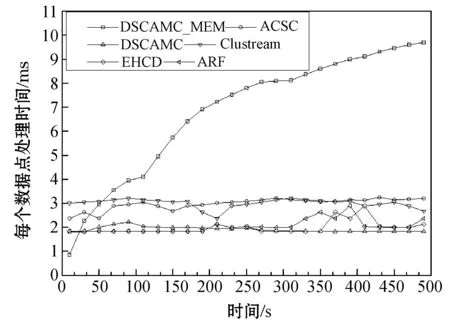
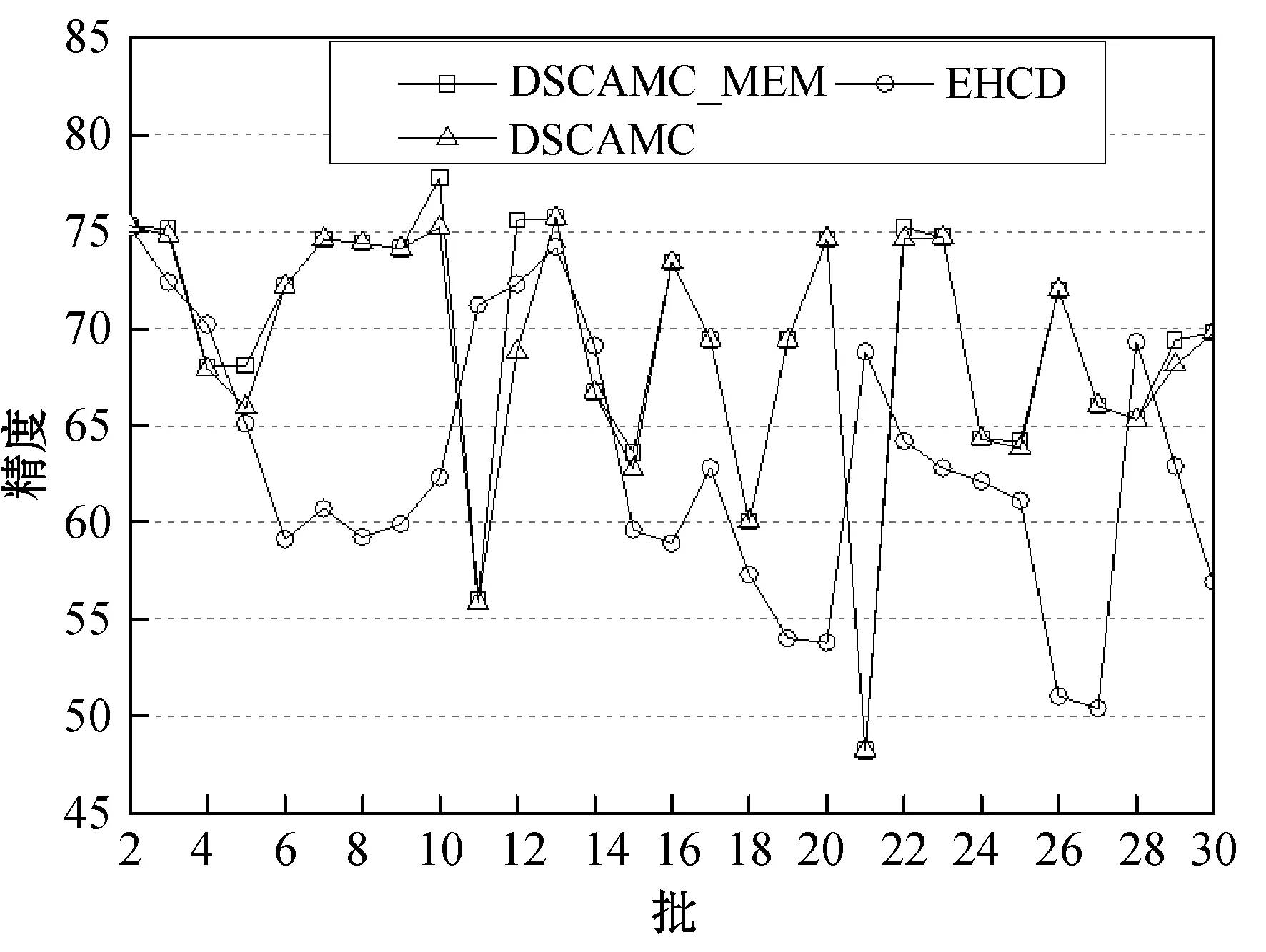
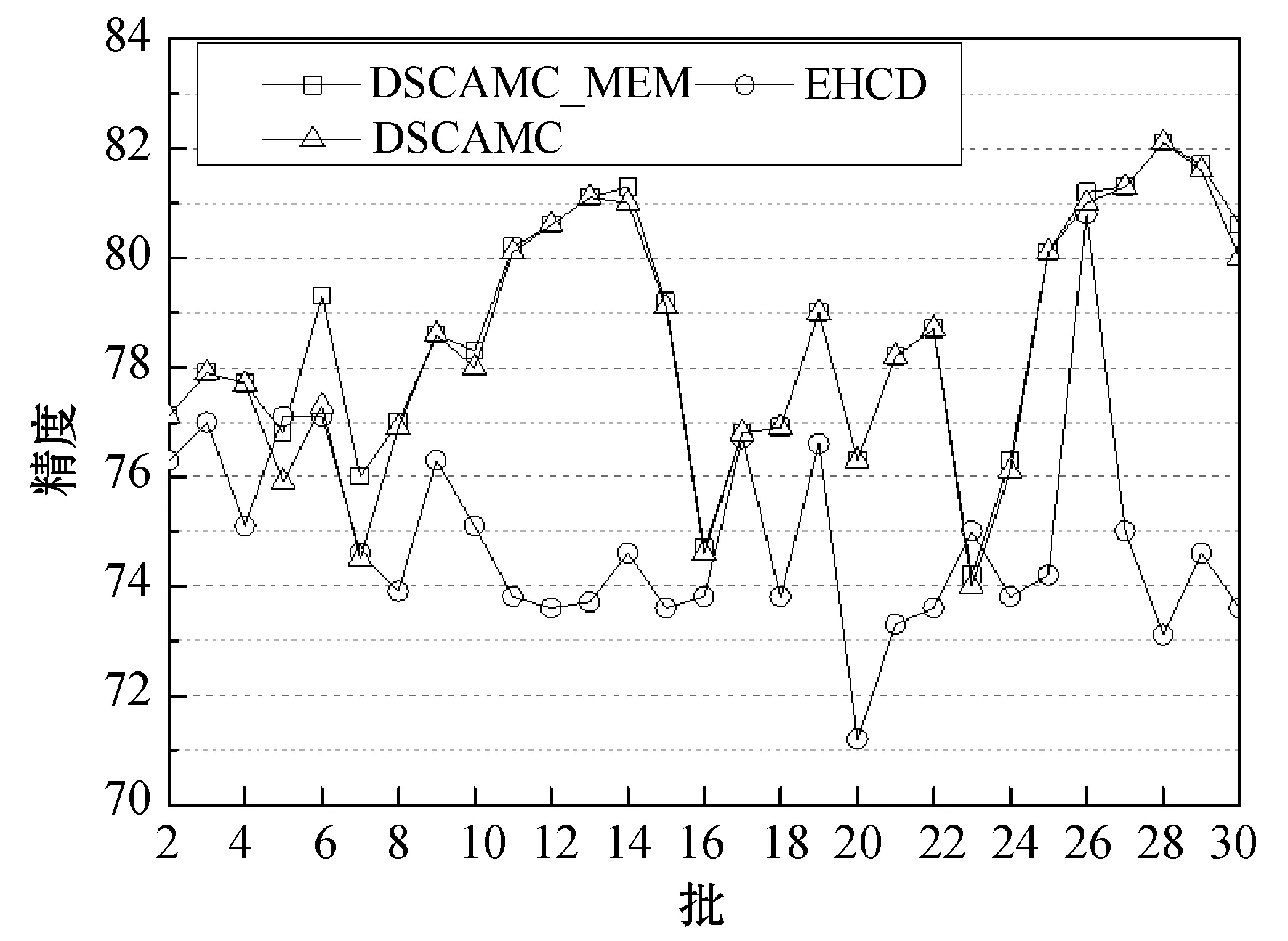
定义4将孤立微簇记为MCout(N,N′,C,R,E,EL,M),孤立微簇应满足以下条件:N 核心微簇和弱微簇的能量都是正值,核心微簇保存于主内存,弱微簇保存于缓存。核心微簇主动加入簇图,并且分配了宏簇ID,而弱微簇未被加入簇图,且未分配宏簇ID。潜在微簇和孤立微簇也未被加入簇图,且未分配宏簇ID。将孤立微簇视为噪声数据,直接删除。 设DeDe表示数据流每个单位时间到达的数据点数量,该变量描述了数据流的速率,设Rmax和Rmin分别表示微簇的最大半径和最小半径,设Thden表示一个核心微簇所需的最少数据点数量,设数据流为X={X0,X1,…,Xn}。DSCAMC算法的训练程序包含7个步骤: (1) 初始化微簇。 (2) 搜索目标微簇。 (3) 更新微簇。 (4) 弱微簇移入缓存。 (5) 清除缓存的弱微簇。 (6) 更新簇图。 (7) 更新最优路径森林。 DSCAMC聚类程序首先输入应用相关的聚类参数(DeDe,Rmax,Rmin,Thden)。当数据点Xi到达,计算Xi和超微簇之间的欧氏距离,搜索其目标微簇T。在核心微簇、弱微簇和潜在微簇中搜索目标微簇,如果成功找到目标微簇T,则提取T的信息;如果未找到,则创建一个新的潜在微簇。更新每个微簇的能量,同时在核心微簇集内搜索候选弱微簇,在潜在微簇集内搜索候选孤立微簇,在弱微簇集内搜索候选死亡微簇。具体搜索方法为:如果核心微簇E≤0,那么该微簇为候选弱微簇;如果一个弱微簇E≤0,那么该微簇为候选死亡微簇;如果一个潜在微簇E≤0,那么该微簇为候选孤立微簇。 1) 初始化微簇。将未分簇的数据点创建一个新微簇MCnew,初始化微簇的特征向量,将该数据点作为微簇的中心,初始化半径设为R=Rmin。局部密度和边缘区域的数据点数量均设为1,即N=N′=1。连接列表EL设为空集,初始化能量设为1,即E=1。新生成微簇的局部密度小于密度阈值,所以MCnew的微簇类型为潜在微簇,通过并集运算将新创建的微簇加入潜在微簇集中: MCpot=MCpot∪MCnew (3) 新微簇的宏簇ID设为M=0。 2) 搜索目标微簇。每当一个数据点到达,DSCAMC计算数据点和每个微簇中心的欧氏距离d,如果距离d小于微簇的半径,该微簇即为数据点的目标微簇。方法定义为: d(Xi,C) (4) 目标微簇可能为以下三种情况: (1) 缓存中核心微簇集的一个弱微簇MCwea。 (2) 潜在微簇集的一个潜在微簇MCpot。 (3) 核心微簇集的一个核心微簇MCcore。 图4是DSCAMC搜索目标微簇的流程框图。首先搜索缓存内的弱微簇集,从时域相关的微簇集寻找相关微簇。如果未找到弱微簇,然后搜索潜在微簇集。如果这两个步骤均失败,则在核心微簇集内寻找目标微簇。 图4 搜索目标微簇的流程 Nt+1=Nt+1 (5) 图5 更新微簇的流程 如果T是弱微簇MCwea或潜在微簇MCpot,并且局部密度大于阈值Thden,则将T加入核心微簇MCcore内。如果T已经是一个核心微簇MCcore,则递归地更新它的半径Rt+1。如果数据点在微簇的边缘区域,则递归地更新微簇的半径。将数据点和微簇边缘的接近度定义为[{2d(Xt+1,Ct)/R}-1],更新微簇半径的方法定义为: (6) 微簇半径不会超过最大值Rmax,仅当新数据点位于边缘区域,才会更新微簇的中心点Ct+1,该机制可以减小微簇的更新频率。如果新数据点出现在边缘区域,通过式(7)和式(8)分别更新N′t+1和微簇中心Ct+1。 N′t+1=N′t+1 (7) (8) 式中:k=1,2,…,D,D为数据点的维度。 借鉴重引力搜索算法的思想评估微簇的密集程度,为每个微簇定义能量函数,微簇的能量增益跟数据点和微簇中心的距离成反比例关系,核心微簇的能量更新方法为: (9) 如果是弱微簇,那么它的能量Et+1设为1;如果是潜在微簇,且密度Nt+1≥Thden,那么它的能量Et+1也设为1。在图5中,如果目标微簇T是潜在微簇,局部密度Nt+1达到阈值Thden,那么将T转化为核心微簇,加入核心微簇集MCcore内。 4) 弱微簇移入缓存。新数据点分簇完成后,减少每个核心微簇的能量,该机制和进化数据流的进化属性吻合,将能量低于0的核心微簇修改为弱微簇。核心微簇T的能量E≤0,说明微簇在时域不相关,将此类型的弱微簇移入缓存。将缓存内的微簇从簇图内删除。对移入缓存的弱微簇作以下处理:(1) 删除T的边,EL=∅。(2) 删除T的宏簇,M=0。(3) 从核心微簇集删除T。(4) 重设T的死亡能量,E=0.5。(5)T移入缓存的弱微簇集。 5) 清除缓存微簇。如果核心微簇的能量减少,那么缓存的弱微簇能量也随之减少1/De。将能量小于等于0的弱微簇称为一个死亡微簇,从缓存内清除。图6所示是识别和清除缓存微簇的流程框图。将能量值小于等于0的弱微簇设为死亡微簇,从缓存内删除死亡微簇。每个潜在微簇的能量也逐渐降低,将能量小于等于0的微簇视为孤立微簇,从缓存内删除孤立微簇。 图6 清除缓存微簇的流程 6) 更新簇图。在以下4种情况下更新簇图: (1) 潜在微簇满足最小密度阈值,转化为核心微簇。 (2) 弱微簇包含当前的数据点,转化为核心微簇。 (3) 核心微簇的中心被修改。 (4) 核心微簇被放入缓存,转化为弱微簇。 上述4种情况下微簇的连接列表可能发生变化,因此需要修改宏簇的数量。前两种情况将新顶点加入簇图,计算交叉的微簇,然后更新微簇的边列表EL。如果两个核心微簇T和T′的半径分别为R和R′,那么两个微簇的交叉距离d′计算为: (10) 如果边缘列表EL发生变化,基于新的EL更新宏簇的数量。对于第(3)、第(4)种情况,删除簇图中对应的顶点,将目标顶点和相关连接从簇图中删除,更新簇图中宏簇的信息。 7) 更新最优路径森林。基于第2节的模型更新最优路径森林OPF,采用当前时间t的OPF聚类t+1的数据流。 实验环境为PC机:Intel Core i5- 4690处理器,16 GB内存,Windows 10操作系统。基于MATLAB R2014A实现实验的算法,从开源软件管理平台github(https://github.com/jppbsi/LibOPF)获取最优路径森林OPF的源代码,然后基于文中每个聚类步骤的程序实现总体的DSCAMC数据流聚类算法。 本文算法简称为DSCAMC,也是完全在线的数据流聚类算法。同时测试本文算法在全部内存情况下的聚类性能,即对于每批新到达的数据均基于所有历史数据重新训练分类器,将全部内存的方法简称为DSCAMC_MEM,DSCAMC和DSCAMC_MEM的差异如图7所示。选择经典的Clustream算法[14]作为对比方案,EHCD[17]作为另一个对比方案,EHCD检测概念漂移的准确率较高,并且对于数据流的聚类准确率也较为理想。选择ARF[18]作为另一个对比方法,ARF基于自适应随机森林实现了对进化数据流的实时聚类,将该算法与本文算法比较,能够观察本文最优路径森林的有效性。ACSC[19]是一种基于密度和人工蚁群优化算法的数据流聚类算法,选择该算法与本文算法比较,能够观察本文算法基于密度聚类的效果。 图7 DSCAMC和DSCAMC_MEM的差异示意图 实验采用合成数据集和真实数据集,合成数据集能够更好地观察概念漂移的聚类效果。表1是合成数据集的主要属性,Hyperplane数据集每隔10 000个样本人工加入概念漂移处理,SEA数据集每隔15 000个样本人工加入概念漂移处理。将每个数据集划分成30个等量的批来模拟数据流,例如:SEA数据集共有60 000个样本,每个批为2 000个样本,因为每隔15 000个样本发生概念漂移,所以每隔7.5个批数据流发生变化。此外采用网络入侵数据集KDD CUP 99作为真实benchmark数据集,KDD CUP 99是一种不平衡数据集,每个攻击类型数据点的形状各异,能够观察本文算法对不同形状数据分布是否有效。 表1 合成数据集的基本属性 上述数据集均为稳态数据集,而本文算法是一种完全在线的聚类算法,数据点在聚类之后立刻从内存中删除,所以需要对实验数据集进行处理。采用Mackey-Glass时间序列生成方法处理: (11) 采用4阶龙格-库塔(Runge-Kutta)法计算式(11)即可产生在线的数据流,最终KDD CUP 99共产生了500 s的数据流。将进化数据流的进化参数DeDe设为1 000个数据点。 精度acc能够评估不平衡数据集的分类性能,因此采用acc作为性能评价指标: (12) 式中:i=1,2,…,c是数据集的分类;E(i)是类i的总误差。 (1) 参数敏感性实验。基于KDD CUP 99数据流测试本文算法的参数敏感性,本文算法包含密度阈值Thden和微簇范围Rmin~Rmax两个参数,通过实验评估算法性能对参数的敏感性。将Thden从1增加至6,观察算法性能的变化情况,Dede=1 000,Rmin=0.06,Rmax=0.12。图8是不同Thden的实验结果,在大部分时间的聚类准确率均接近100%,在150 s时因为数据发生剧烈的变化,准确率出现明显的降低,在350 s之后数据点也发生明显的变化,导致聚类准确率降低。总体而言,Thden=3时取得最好的效果。 图8 Thden参数的敏感性实验 Rmin分别设为0.04、0.05、0.06、0.07、0.08,分别测试最大半径0.08~0.14的聚类性能,结果如图9所示。可以看出,微簇半径的范围对于聚类性能的影响较小,其中Rmin=0.06、Rmax=0.12时取得最好的聚类性能。 图9 微簇范围的敏感性实验 (2) 对比实验。图10为6个数据流聚类算法对网络入侵数据集KDD CUP 99的准确率结果。可以看出,DSCAMC_MEM由于采用所有可用的数据集训练分类器,所以获得最高的聚类准确率。ACSC是基于密度和人工蚁群优化算法的数据流聚类算法,该算法通过人工蚁群优化算法对微簇的密度进行优化处理,也取得十分理想的准确率结果。DSCAMC则和ACSC的结果接近,相较于DSCAMC_MEM则存在明显的衰减,但DSCAMC的准确率好于Clustream、EHCD和ARF算法。 图10 6个数据流聚类算法对真实数据集的准确率结果 图11为6个数据流聚类算法对网络入侵数据集KDD CUP 99的平均处理时间结果。可以看出,DSCAMC_MEM由于采用所有可用的数据集训练分类器,所以随着时间的推移,其处理时间也快速提高。ACSC是基于密度和人工蚁群优化算法的数据流聚类算法,该算法对每批数据均需要采样人工蚁群优化算法对微簇的密度进行优化处理,平均每个样本的分类时间也较长,在数据量较大的情况下,其效率较低。本文算法是一种完全在线的数据流聚类算法,随着时间的推移也始终保持较低的处理时间。 图11 6个数据流聚类算法对真实数据集的处理时间结果 概念漂移是进化数据流的一个重要问题,采用合成数据集进行实验,便于观察本文算法对概念漂移问题的处理效果。因为ACSC、Clustream和ARF三个算法不支持概念漂移的检测处理,所以将DSCAMC_MEM、DSCAMC和EHCD三个算法进行比较。图12(a)和12 (b)分别是3个算法对于Hyperplane数据集和SEA数据集的实验结果。图中DSCAMC_MEM的结果依然略好于DSCAMC算法,但本文算法也对概念漂移的情况表现出较为理想的响应,在发生漂移的数据点,分类的准确率出现明显的衰减,但是在短时间内即可恢复到较高的准确率。虽然EHCD也成功检测出概念漂移的发生,但是需要很长的时间才能恢复到稳定的状态。 (a) Hyperplane数据集 (b) SEA数据集图12 合成数据集的聚类结果 本文提出基于自适应微簇的任意形状进化数据流聚类算法,设计递归的微簇半径更新机制,自适应地搜索微簇半径的局部最优值。采用最优路径森林组织宏簇的完全图,将能量值最高的微簇作为最优路径树的根节点,根据最优路径将新到达的数据分类。本文算法实现对于进化数据流的完全在线聚类处理方案,对于任意形状的数据集均具有较好的聚类准确率,并且实现了理想的处理效率。 为了保持较高的聚类准确率,防止一些时域相关的微簇被过早地删除,本文通过缓存机制保留一些当前空间域不相关的微簇。未来将深入研究结合计算机的体系架构实现快速且规模小的缓存方案,提高缓存的命中率和匹配速度。
3.2 DSCAMC算法设计
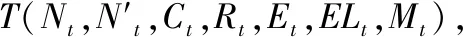
4 实 验
4.1 实验环境和对比方法
4.2 实验方法和benchmark数据流
4.3 性能评价指标
4.4 真实数据流实验
4.5 合成数据流实验
5 结 语
