MX″(t)+CX′(t)+KX(t)=F(t)解析解的两个实例应用

姜 雄，苏中乾

(辽宁科技学院 基础部，辽宁 本溪 117022)

1 一类方程的解析解与数值解

(1) 文献〔1〕方程

MX″(t)+CX′(t)+KX(t)=F(t)

(1)

称为刚性动力方程。

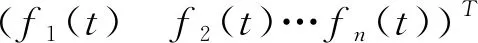
(2)MX″(t)+CX′(t)+KX(t)=F(t)的解析解

文献〔1〕将MX″(t)+CX′(t)+KX(t)=F(t)降阶为一阶方程为：

(2)

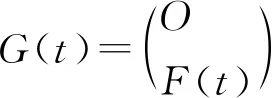
(3)

(4)

(5)

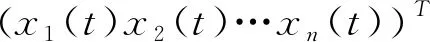
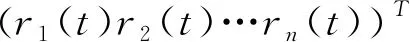
(6)

(7)

其中：V0包括初始条件

V(0)=(x1′(0)x2′(0) ...xn′(0)x1(0)

为了便于计算，由文献〔3〕，定义A=-T-1U，R(t)=T-1G(t)中的A,R(t)可以证明写成：

(8)

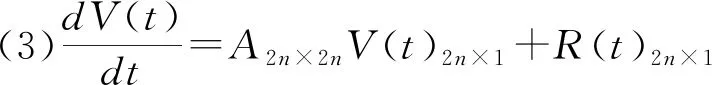
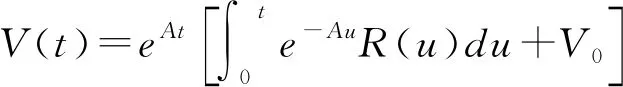
(4)参照文〔1〕将eAt用泰勒展开式的数值计算方法。

(5)参照文〔1〕将e-At用泰勒级数展开数值计算方法。

2 微分方程MX″(t)+CX′(t)+KX(t)=F(t)的实例分析

通过实例来分析方程的解析解。

例1：如图1是粘滞阻尼媒质中的两质—量弹簧系统。

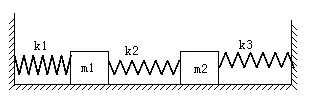
图1

设两质量在一媒质中运动，媒质的阻尼力正比于速度，设质量m1和m2上分别作用推动力为f1(t)和f2(t)，建立x1(t)和x2(t)所需的方程。

解：设阻尼系数C，则运动方程：

矩阵形式为：

即MX″(t)+CX′(t)+KX(t)=F(t)，是文献〔1〕的微分方程。

由(8)得：

将A,R(t)带入(8)式，

但是，eAt是难以求出的，所以，当矩阵A的秩大于2时，解析解(8)只能是形式上的。

下面通过实例，来运行数值解的过程。

例2：如图2所示。

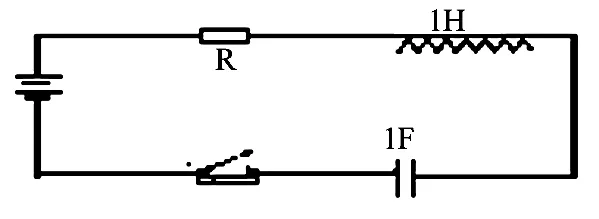
图2

开关S在t=0时闭合的简单RLC环路。

试计算开关闭合后t=0.3秒时环行电流和电荷，初始电流电荷为零，选择0.1秒。

解：由克希霍夫定律〔4〕，有：

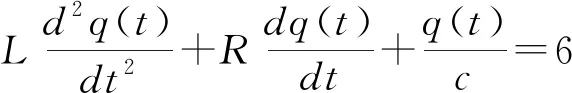
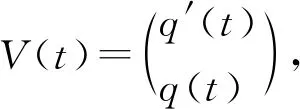
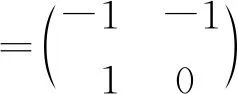
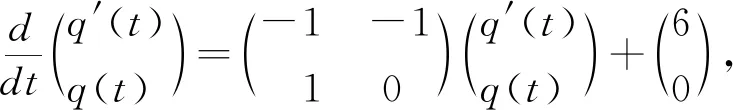
当t=nh，

[R((n-1)h)+R(nh)]

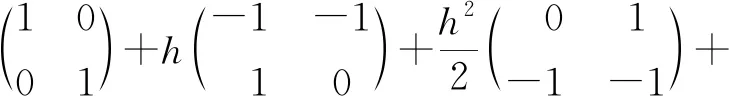
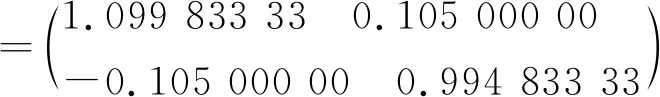
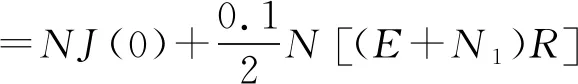
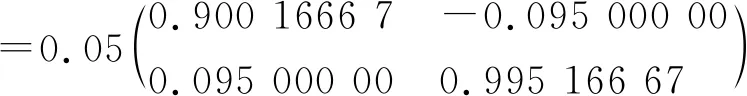
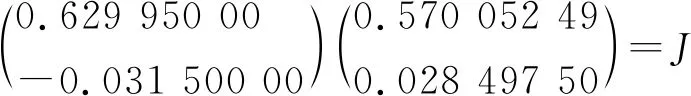
当n=2，V(0.2秒)

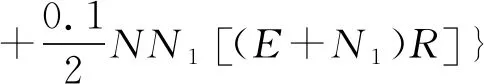
=N{J(0.1秒)+NN10.05[(E+N1)R]}

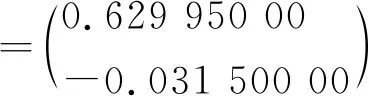
V(0.2秒)=N{J(0.1秒)+NN10.05[(E+N1)R]}

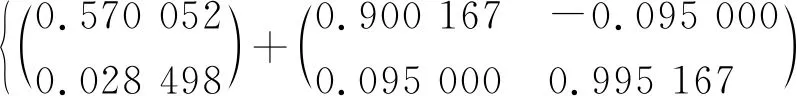
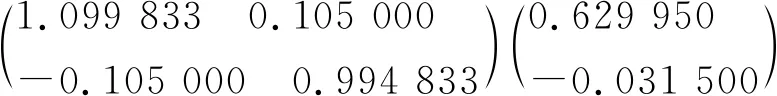
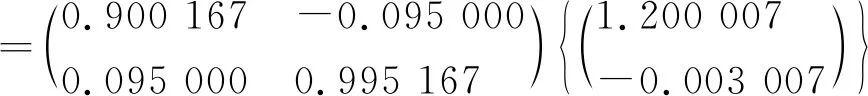
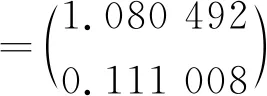
=J(0.2秒)

当n=3，V(0.3秒)

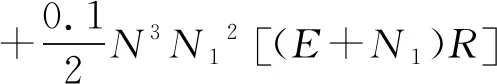
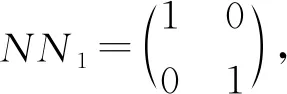
V(0.3秒)=

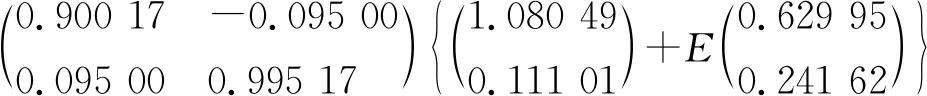
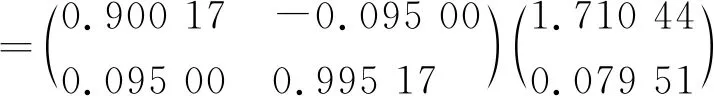
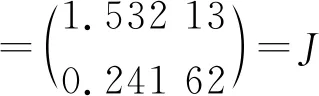
所以，开关闭合后，当t=0.3秒，q′(t)=1.532 13A，q(t)=0.241 6C

通过实例分析，我们对刚性方程的解进行了简单的讨论。考虑到微分方程MX″(t)+CX′(t)+KX(t)=F(t)的解析解计算复杂，尤其当矩阵的阶很大时，计算量变得庞大，其数值解可以用简单的程序完成。但这里就不做阐述， 我们只是强调方程的解法极其模型的建立过程。