改进型卷积神经网络焊点缺陷识别算法研究

常 颖，常大俊

(1.吉林建筑科技学院 计算机科学与工程学院， 长春 130000； 2.长春建筑学院 电气信息学院， 长春 130000)

引 言

随着工业4.0与我国“智能制造2025”计划的不断深入发展，电子产品焊接质量的自动识别、智能检出也成为热门话题，因为对焊点质量的检测是保证产品质量的重要环节[1]。智能检出技术的有效应用离不开机器视觉，而通过机器视觉判断的核心是图像识别处理算法[2]。电子产品焊点的焊接形式各异，焊接程度要求标准也不同，传统的识别算法已难满足日益增长的测试需求，开发具有更好识别能力的算法具有重要意义。

为了实现对印刷板电路(printed circuit board,PCB)[3]中的焊接异常进行识别，有效地机器视觉配合具有自适应、自学习的识别算法成为了当前的研究热点。尤其针对密度大、元件小的产品批量监测需求，研究开发快速准确、具有一定适应性的图像识别算法是十分必要的。现有PCB焊接问题主要包括桥连、小球、虚焊、焊珠、空洞等问题[4-6]，传统的机器视觉检测往往是通过将拍摄照片与标准照片进行对比完成的。这种方法对于缺焊、空洞的识别率非常高，几乎不存在漏检或误检，但对锡量过大或少锡的情况识别效果很差，漏检率高,同时，当焊点不均或者边界欠清时还会出现检测类型有误的现象。这些问题的产生主要是因为识别算法不具备学习能力，或者自适应性不强。

为了提高该类情况的检出效果，有多种方法被尝试,如反向传播(back propagation,BP)算法[7]、k均值近邻法[8]、支持向量机(support vector machine,SVM)[9]、深度学习法[10]等。BP算法思路成熟但收敛速度慢，容易产生局部极值[11]；k均值近邻法简单易实现、但无学习能力，拍摄图片效果稍有差异就会造成识别精度大幅下降[12]； SVM具有学习指向性，能够从一定程度上解决图片差异的问题，但面对当前焊接异常类型的不断增多，大样本的训练导致其识别速度大幅下降[13]。相比之下，深度学习识别能力强、速度快，更适合智能制造的需求。本文中提出了一种基于深度学习的快速焊点异常识别算法，其具有低误检率、低漏检率、高速响应的特点，可应用于智能制造中的快速焊接质量检测。

1 系统设计

在焊接质量检测过程中，希望获得低误检率和低漏检率。误检率(false detection rate,FDR)指错误判断采集图像，将正常焊点误判为异常焊点的比率。漏检率(missed detection rate,MDR)指将有焊接质量问题的焊点误判为正常焊点，从而漏掉检出问题焊点的比率。系统由X射线源、机械控制转台、数据处理系统、像增强器、CCD以及图像采集卡构成。测试系统及其采集获取得到原始图像如图1所示，图中矩阵表示原始图像中每个焊接点Sij对应的矩阵位置。

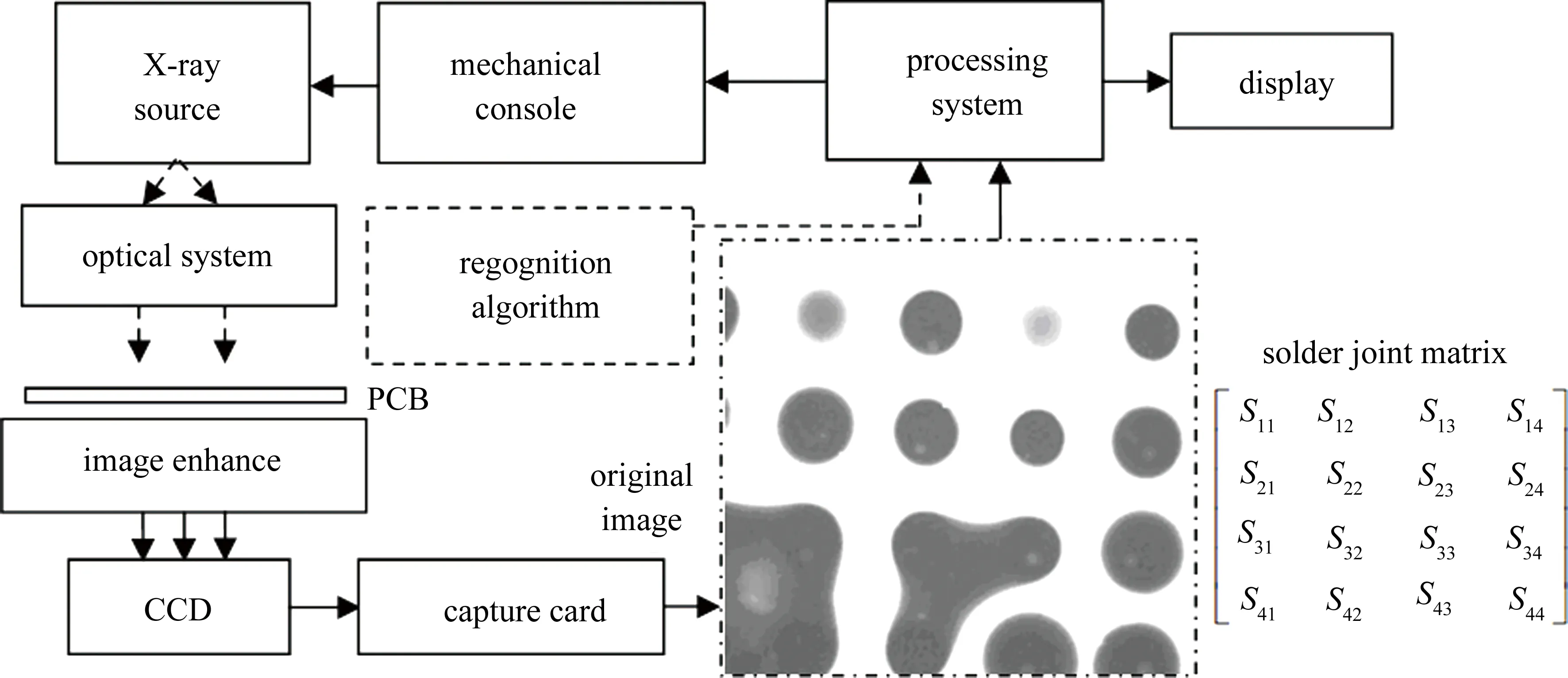
Fig.1 Diagram of the system structure

2 数据预处理

为了实现快速焊点质量检测，需要对原始图像进行预处理，即图像增强、均衡化处理以及平滑补偿，从而突出待测图像特征，降低焊点异常提取的难度。由于相机对环境光强变化的动态适应性有限，故首先对照明变化导致的成像质量差异进行预处理,利用图像增强技术调节原始图像亮度范围，本系统中采用了直方图均衡配合灰度拉伸算法完成图像灰度调节。算法步骤如下。

2.1 获取灰度直方图函数

将原始图像中的灰度直方图均匀化分布，使每个灰度级对应的像素数一致，进而增加其动态范围。设图像灰度级为横坐标，灰度级像素出现频率为纵坐标，灰度级∈[0，L-1]，则灰度直方图函数可表示为:

h(rk)=nk,(k∈[0,L-1])

(1)

式中，rk为第k个灰度级，nk为灰度级rk的像素数,L表示图像的最大灰度值。

2.2 图像增强

通过灰度拉伸算法对图像中每个点的灰度值进行拉伸处理。设f(x，y)为原始图像，其灰度级∈[l1，l2]。为了得到[l3，l4]范围内图像函数g(x，y)，需要进行转换，转换函数可表示为

T=(l4-l3)(l2-l1)-1(r-l1)+l3

(2)

式中，r表示图像像素点的灰度值。由此可见，经过拉伸函数处理后，图像中所有像素点的灰度值均完成灰度变换，图像对比度得到提高，实现图像增强。

2.3 滤波优化

为了降低焊点图像的不均匀性，抑制杂散光等的影响，选取平滑算法优化图像质量，提高图像信噪比。采用中值滤波的方式对所有像素对应值进行排序处理，对所选图像区域所有像素点灰度值取中值Qmid，其图像矩阵可写为:

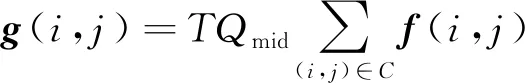
(3)

式中，(i,j)为算法选择区域中滤波区域对应的像素位置，(i,j)在图像边界区域中，C表示图像区域。由于中心像素选取的灰度值是根据原始像素及其相邻像素的灰度值统计分类获得的，故本滤波算法可用于非线性图像处理。利用此中值滤波算法可以剔除误差较大的孤立像素，对图像全局影响不大，同时大大降低离散噪声对图像的影响。

3 焊点异常识别算法设计

3.1 深度学习算法构架

深度学习(deep learning,DL)[14]是学习样本数据的内在规律及表示层次的一种数据处理方法，属于机器学习算法的一个方向，重点应用于图像识别方面。其中，深度学习算法中具有深度结构反馈运算特性的有卷积神经网络(convolutional neural network,CNN)[15-16]，可对原始图像样本进行数据处理。其结构由输入层、卷积层、汇集层、连接层和逻辑回归层构成。系统通过卷积核实现卷积操作，指示符为长度、宽度及深度，其卷积神经网络传递函数的表达式有:

S(i,j)=(I*K)(i,j)=

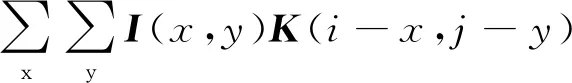
(4)

式中，I为图像矩阵，*表示卷积，K(i-x,j-y)为卷积核。x和y为i和j像素点对应的图像位置，x和y的集合为焊点区域。将相邻像素点与卷积核对应点相乘再求和，获得该点的像素值，该操作遍历每个像素点，从而得到卷积神经网络的前向传播。

3.2 改进型卷积神经网络

卷积神经网络属于前馈式神经网络，训练样本不需要太大，最重要的是其对图像畸变、模式变化具有较高的容错能力，所以对大量焊接图像不同缺陷类型具有较好的兼容性。该网络结构由输入层、卷积层、降维层、连接层以及输出层构成。焊接图像进入输出层后与核函数进行卷积，由激励函数输出神经元，实现特征图像的获取并进入下一层。设第n卷积层的第j个特征为:

(5)

式中，f()为激励函数，Nj为上层特征图像集合，ki,j,n为卷积核权值，bj,n为和偏置。获取特征后导入降维层减小运算量。则第n降维层第j个特征图有:

Yj,n=f(ηg(Yj,n-1)+bj,n)

(6)

式中，g()为降维函数，η为积偏置。

因为焊接异常图像特征本身具有多样性，每种缺陷虽然存在相似性，但尺寸面形仍具有较大差异，所以需要具有数据选择的自适应性，由此提出了通过对数据自组织映射实现对卷积神经网络的改进。

设输入数据样本为xi,p(p=1,2…,m,i为分量)，输出为Cij，则输出方程有:

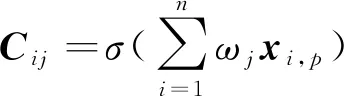
(7)

式中，σ( )为单调函数，ωj为第j个神经元的权值。利用赫布规则化简可得:

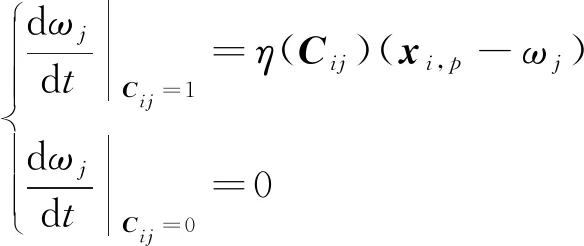
(8)

式中，t是时间。

由此得到输出层相当于具有中心分布的样本数据，然后利用训练网络与学习网络配合实现数据分类的加速收敛。

3.3 模型设计与实现

在改进型卷积神经网络框架基础上构建焊接质量识别算法的模型，其中，损失函数利用Cross Entropy实现。在本算法中利用反馈数据自适应的方式完成，从而依据每次的测试结果进行参量调整。基于自组织映射的卷积神经网络算法参量设置与实现步骤如下:(1)在训练网络中设卷积神经网络的核函数、激活函数等，确定学习速率初值并构建邻域初值；(2)将标记样本导入训练网络，由(5)式和(6)式获取特征样本；(3)在邻域权值竞争基础上完成异常图像特征点调整，并将获得的新特征点加入样本标记；(4)将训练网络导入学习网络，迭代寻找最优值。

其工作流程如图2所示。

Fig.2 Flow chart of an improved CNN model

4 实 验

4.1 数据获取

实验中选用UNIQ-3000型CCD相机完成焊机图像采集，共采集5000张，其中包括焊接良好和焊接异常两大类，焊接异常中分为小球、桥连、虚焊、少锡、偏球5种类型。3000张焊接图像构成算法模型训练集，1000张焊接图像构成模型验证集，1000张焊接图像用于测试。基于深度学习的焊接异常识别算法在Ten-sorflow环境下采用Python编译实现。

4.2 焊接异常图像对比

为了检验对比基于深度学习的焊接异常图像识别算法的效果，对其漏检率与误检率量化分析。与传统的canny边缘提取算法进行对比，从而考察本算法在边缘特征信息保留方面的性能；同时，与k均值聚类算法进行对比，从而考察本算法在特性分类方面的性能。同时采用3种方法针对5种典型焊接异常进行识别检测，3种方法获得的处理结果如图3所示。

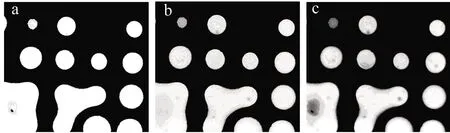
Fig.3 Image recognition result of welding abnormality

由图像处理结果可知，canny算法的边界处理效果最好，清晰度高、对比度强，有利于识别桥连和小球类型的焊接异常(例如桥连缺陷S32和S33、小球缺陷S23)，但焊点中的分布信息被明显削弱，造成对虚焊、偏球、少锡类型的焊接异常识别能力降低。k均值算法的边界处理效果虽然清晰度不如canny算法好，但采用反馈型阈值解析仍可以获得很好的边缘检测精度。另外，k均值算法获得的焊点图像仍保留了同灰度级的差异，可有效地识别偏球缺陷(例如偏球缺陷S12)，但对虚焊和少锡的特征分类效果并不明显。本算法中边界处理效果与k均值算法相近，同时，焊点特征保留更为明显，不但有表征偏球缺陷的同灰度级差异，还有梯度变化信息，可以对虚焊和少锡问题进行阈值量化分析(例如虚焊缺陷S24，少锡缺陷S22)。对验证集的检测结果进行统计分析，获得3种方法漏检率与误检率数据分布如表1所示。

由测试结果可知，3种算法对桥连的判断都能达到100%识别，即误检率和漏检率均为0，分析认为桥连的图像范围大，易识别；相比而言，小球缺陷的检测对边界特征信息要求更高，canny算法的边界处理效果更好，其误检率和漏检率均低于k均值算法和本算法；对于偏球缺陷而言，其不但涉及边界分布还需考虑焊点灰度分布特性，canny算法的识别效果最差，k均值算法优于canny算法，本算法效果最好，误检率与漏检率相比canny算法减小了一个数量级；对于虚焊和少锡缺陷而言，都需要对焊点的灰度分布梯度进行解析，传统的两种算法测试效果相近，本算法识别精度有所下降，但总体水平仍优于前两种方法。实验结果表明，相比传统图像分割算法,本算法可以更好地获得各种焊接缺陷图像，从而为焊接质量分析提供了更好的支撑。

Table 1 Comparison of missed detection rate and false detection rate of three methods

4.3 测试集分析

算法验证后采用未知缺陷分布情况的焊接图片进行测试，将1000张测试图片分别输入3种算法后迭代运算，分类后完成数据统计分析，对误检率、漏检率和召回率进行统计。为了对图像测试数据进行综合评价，在1000张测试图像中等比例插入了5种不同缺陷形式的焊接图像。统计结果显示，canny算法在测试集中的误检率为7.8%、漏检率为9.7%、召回率为90.75%；k均值算法在测试集中的误检率为7.4%、漏检率为8.3%、召回率为92.15%；本算法在测试集中的误检率为1.6%、漏检率为1.7%、召回率为98.45%。由此测试集统计数据可知，3种算法的识别能力与验证集中各测试结果的加权平均值相近，说明基本可以表征各算法的实际测试效果，也验证了本算法具有更好的焊接异常检测识别性能。

5 结 论

针对传统焊接异常识别算法对不同焊点缺陷识别能力差异大的问题，提出了一种基于深度学习的焊接异常识别算法，利用卷积神经网络完成自适应矩估计计算，并结合5000幅焊接图像进行训练测试。实验结果显示,本算法在5种常见焊接异常情况下均能很好地完成焊点缺陷的识别，验证了其在快速电路板检测应用领域具有一定的应用价值。