基于CPSO 算法在风电接入时无功优化的应用研究

2020-11-11赵柏翔关焕新

沈阳工程学院学报（自然科学版） 2020年4期

关键词：定子发电机粒子

赵柏翔，关焕新

（沈阳工程学院a.研究生部；b.新能源学院，辽宁沈阳 110136）

1 双馈式风力发电机特性分析

双馈式风力发电机组在定子侧与转子侧分别采用发电机与电动机的转动惯例，如图1所示。

图1 双馈式风力发电机等效电路

等效图对应的基本方程组如下：

图1 中Pr、Ps、Qr、Qs分别表示为转、定子的有功、无功功率。将转子侧电抗折算至定子侧。

式中，Xs为定子侧励磁电抗；Xr为转子侧励磁电抗。

通过DFIG 的基本方程和等效电路图可知，变频器不仅为双馈式发电机提供定子电源，还可以调节转子转速，追踪最大功率。根据以上公式可以得到转子电流的表达式为

注入系统有功与无功为

定子侧有功功率Ps和无功功率Qs选定范围受定子绕组、转子绕组和变流器转子端的电流大小的限制影响。为推算每台双馈式发电机的最大无功功率输出能力，需要选取最大运行电流，假设Irmax为1.4倍额定电流。

忽略转子侧无功，每台风力发电机的无功全部由定子侧等效，即单机极限功率表达式为

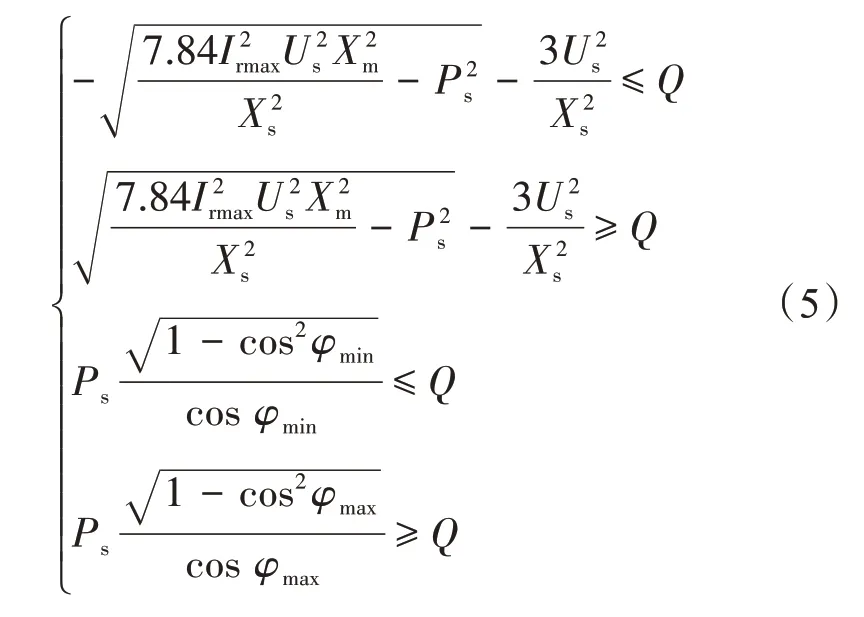
式中，cos2φmin、cos2φmax分别为功率因数的上限与下限；Q为每台双馈式发电机最大无功输出功率。当功率因数最大时将失去无功调节能力。

2 STATCOM运行原理及特性

STATCOM 的运行原理与SVC 基本相同，都是可以等效为可调电压源，可利用全控型元件GTO控制连接电网的电压源最大值与相位，以改变电网输送的无功大小。STATCOM 实际上也是一个自换相全波桥式逆变器，原理如图2所示。

图2 STATCOM原理

可控电压源电压根据自身与电网电压的高低判断无功的输出类型，若高于系统，则向系统输送感性无功，否则向电网输送容性无功。STATCOM输出电压控制模式分为移相调压与脉宽调制两种。保持脉宽θ不变，只调整相角δ就可以改变STAT‐COM 向系统输出的无功大小，电容电压也随之发生改变，同时调整θ、δ就可以保持电容电压不变，只改变无功功率的大小。STATCOM 向系统输送的无功功率为

以南瑞继保35 kV 电压等级Y 型STATCOM 为例，其损耗与容量的关系如表1所示。

表1 STATCOM的损耗与容量百分比关系

根据表1 中数据可知，随着容量的增加，损耗值也随之增加，但损耗占容量的份额基本保持不变，甚至有下降的趋势。

3 多目标无功优化数学模型

本次优化以电力系统线路的有功网损最小及线路各个节点的电压偏差最小为目标，动态优化目标公式可以表达为

式中，i、j为始末节点；f1为风电场并网时未进行优化的系统有功功率损耗；f2为风电场并网时未进行优化的系统各节点电压偏差之和；Ui为i节点电压幅值；UN为节点的额定电压，节点电压幅值的选取应当满足系统的安全性与合理性。

3.1 约束条件

潮流约束方程为

3.2 罚函数策略

为了提升最优解的准确度，化解不等式约束，需要引入罚函数和惩罚因子的概念。罚函数是在原函数的基础上增加的障碍函数，目的是得到增广目标的函数。罚函数的作用在于规定某极大值，限制可行域内点的运动轨迹，禁止粒子企图穿越或逃离界限，将有约束的策略优化问题转换为无约束的策略优化。

惩罚因子的作用是衡量损失的权重，其取值的大小对分类隔离的重视程度相关。如果惩罚因子较小，算法计算失误的惩罚力度小，修正效果不明显，此时就需要加大惩罚因子的值；若过大就会导致罚函数接受未知数据的能力削弱。不同节点的惩罚因子的最佳值也各不同，从理论上讲，每个节点惩罚因子分别赋予最佳求解效果，但又会提高系统的复杂程度。

式中，FP为目标函数有功部分的适应度；FQ为目标函数无功部分的适应度；Ui为节点i的电压；Qi为需要补偿的无功大小。

式中，F(x)定义为最终适应度；FP为满足不等约束时的目标函数值；FQ为满足不等约束时最小目标函数值；CU(x)为状态量x的所有约束和。

为方便运算，把控制变量解约束作为罚函数的形式计入到目标函数中。添加罚函数及惩罚因子的作用：

1）限制了最优解的范围，避免了粒子算法陷入局部最优；

2）避免了由于复杂的计算过程及限制条件的不到位而造成的解质量下降的问题。

4 混沌粒子群算法

4.1 传统PSO算法

PSO 是高维空间内对人类思维和行为的智能模拟，首先建立一个n维的搜索空间，在空间内布置10～20 个粒子，对每个粒子赋予位置和速度矢量，表示如下：

粒子经历的最优位置Pb和种群最优位置Gb表示如下：

当粒子感知到最佳位置时，其他粒子就会在该粒子周围重新布置，通过公式迭代得到速度矢量与新位置：

式中，c1、c2为学习因子，传统PSO 算法学习因子值为2；惯性权重ω为0.8；r1、r2为（0，1）间随机数。

粒子速度的选择关系到结果的精确度，速度过快，会使搜索陷入局部最优；过慢不仅会加大迭代次数，增加运算量，还会降低搜索精度。

4.2 混沌优化

混沌优化算法具有遍历性，对初始值反应快，具有易跳出局部最优的特点且搜索最优粒子能力较强。由于其在局部寻优上优势突出，同时可以简化迭代过程，本文为方便操作，通过一维Logistic函数进行迭代：

当μ=4 时，系统会进入完全混乱状态，从公式可知，不含有其他参数。在寻优的过程中，对粒子迭代进行混沌优化。

式中，Pb(x)、P'b(x)分别表示混沌优化前后的粒子最优位置值。

优化前先对个体映射，对优化后的粒子重新计算适应度，若适应度更优，则选取变异粒子；否则，继续迭代，直至达到要求值。

4.3 算法流程

基于多目标函数的混沌粒子群优化算法的电力系统无功优化流程如图3所示。

图3 混沌变异粒子群算法寻优流程

5 算例分析

为了说明混沌粒子群算法在无功补偿应用中的优越性，利用MATLAB 对IEEE30 系统进行仿真，并与PSO算法优化网络损耗和节点电压结果对比。由于本文关注点只在于网损与无功偏差，为简化研究过程，将系统中发电机视为风力发电机，IEEE30节点系统拓扑结构如图4所示。

图4 IEEE30节点系统拓扑结构

该系统由6 台发电机、4 个可调变压器、2 个补偿节点、41分支组成。平衡节点、PV 节点、PQ 节点电压规定为0.95～1.05 p.u.，设置PSO 算法与混沌粒子群算法的种群数为10，ωmax=0.8，ωmin=0.3，c1=c2=2，以最大迭代次数为150 次为结束条件，每个粒子在10 维空间内寻求最优解，网络总负荷为5.045+j2.498 MW，系统三相功率的基准值为10 MVA，在节点24、25 间添加SVG。在150 次迭代过程中，CPSO无功优化中的网损与电压偏差的变化情况如图5 所示。IEEE30 节点检测量及节点电压优化结果对比如表2所示。

图5 网损与电压偏差的变化

表2 IEEE30节点检测量及节点电压优化结果对比

从表2 可知，未用算法优化的网损为570 kW，采用传统粒子算法与混沌粒子群算法优化的网损分别为520 kW 与510 kW。PSO 与CPSO 无功优化网损与电压偏差关系如图6 所示，从图中可以看出CPSO 的优化效果优于传统PSO。由于随着SVG容量投入的增大，电压偏差指标减小，网损呈递增趋势，因此需根据风电场具体情况，选择合适的无功投切容量。