面向集合计算的隐私保护统计协议

宋祥福 盖 敏 赵圣楠 蒋 瀚

1(山东大学计算机科学与技术学院 济南 250101) 2(山东大学软件学院 济南 250101)

目前，通过共享分散于多机构的孤立数据、挖掘其中蕴含的潜在价值，从而服务于政府决策以及提高服务质量，已经成为一种客观需求.然而，在很多场景下，数据持有者往往有隐私需求，并且待分享的数据通常包含一定的商业价值，因而数据持有者不想揭示持有数据的明文信息.况且，国内外关于数据安全的法律法规，如欧洲的数据保护总条例(general data protection regulation, GDPR)和《中华人民共和国密码法》的生效，为数据安全提出了更高的要求.因此，如何在保护数据隐私的前提下，对分散的数据进行融合计算，发掘数据的潜在价值，已经成为学术界和工业界的热点研究问题.

在数据共享场景中，一种典型应用需求是集合求交(private set intersection, PSI).以两方计算为例，参与方P0持有集合X，P1持有集合Y，执行集合求交运算后，双方得到交集结果X∩Y,而不泄露任何其他信息.集合求交可广泛应用于隐私需求较高的保险、医疗、征信等业务场景，如2个银行计算共同客户而不泄露自己持有的客户群体.然而，仅仅计算集合交集并不能满足持续扩大的需求.具体来说，很多场景下，协议双方可能不仅仅满足于交集计算，而想计算集合运算结果的某些函数.比如双方可能只想泄露关于交集的某个函数f(X∩Y)，如交集大小、交集权值和等.在这些应用场景中，很多时候泄露交集元素都是不被允许的.因此，需要对隐私保护的集合运算及性能进行拓展，从而满足法规约束下的越来越多的隐私保护数据共享需求.

通用安全多方计算可以实现以上需求.具体来说，安全多方计算能够允许互不信任的n个参与方P0,P1,…,Pn-1通过协议交互计算某个既定函数f，协议运行结束后，只揭示计算结果y=f(x0,x1,…,xn-1)，除此之外不泄露任何关于输入的信息.虽然近年来基于Yao电路和秘密共享的通用安全多方计算协议的效率得到极大提升，但对于集合运算，专用安全多方计算协议更高效.在本文中提出了计算集合运算统计量的专用安全计算协议.具体来说，在两方计算场景下，设计了计算集合运算统计量的协议架构.利用该协议，参与方可以高效地计算集合交集大小、并集大小以及交集权值和等统计量，而不泄露具体的交集元素.该协议主要利用了茫然传输(oblivious transfer, OT)作为协议的主要密码组件.由于OT可以通过OT拓展协议生成大量实例，从而使得协议具有较好的可拓展性.具体地，本文主要内容包含3个方面:

1) 提出了计算集合运算统计量的一组协议，能够实现针对集合运算的数据统计计算，包括交集大小、并集大小、交集权值和交集权值方差等集合运算的统计信息.

2) 该协议可以仅利用OT作为底层密码组件，因而可以借鉴高效的OT拓展技术实现较好的效率.本文对协议的通信和计算的渐进效率进行了复杂度分析和对比.

3) 在半诚实敌手设定下，利用理想现实模拟对协议进行了安全证明.

1 相关工作

基于Diffie-Hellman密钥协商的PSI协议可以实现较好的通信效率，但是计算效率较低.此类协议[1-2]利用了Hash函数H：{0,1}n→G，其中底层群G为素数阶p且判定Diffie-Hellman问题是困难的.具体来说，参与方P0和P1分别持有密钥k0,k1∈Zp.发送者P1计算Y′={H(y)k1}y∈Y并发送给P0，P0计算X′={H(x)k0}x∈Y并发送给P1.然后P1计算X″={H(x′)k1}x′∈X′并发送给P0.最终，P0计算Y″={H(y′)k0}y′∈Y′，并输出{x|x″∈X″∩Y″}.

基于OT的PSI协议[3-7]由于计算性能友好，近来成为主流设计思路.基于OT的方案主要想法是利用OT来进行等值比较计算.在等值比较协议中，P0输入x,P1输入y，协议结束后P0只能知道x是否等于y.利用这种方法，在最坏情况下，双方对所有可能的元素对执行运算，产生O(n2)的通信和计算复杂度.为了提高此类协议的效率，可以借鉴Hash分桶[8]的思想，将元素映射到Hash表中的每个桶中，然后逐桶执行等值比较.通过合理选取参数，可以达到O(nlogn)甚至O(n)的复杂度.文献[9]提出了一个传输短消息的OT拓展协议.随后，通过对文献[9]中的OT拓展协议进行改进，Kolesnikov等人[10]设计了基于OT拓展的茫然伪随机函数(oblivious pseudorandom function, OPRF)，并将其利用到PSI协议中，实现了ω(n)的复杂度，接近于最优.近来Pinkas等人[11]设计了一个新的稀疏OT拓展协议，能够允许OPRF接收方计算多个点的OPRF输出.利用该OT拓展，可以实现O(n)的通信复杂度.

Dong等人[12]提出了一个高效的基于布隆过滤器的成员测试数据结构——混乱布隆过滤器，并将其应用到集合求交协议中；文献[13]基于混乱布隆过滤器构造了一个恶意敌手下安全的PSI协议.集合求交可利用通用安全计算协议来实现；Huang等人[14]提出利用混乱电路来执行集合求交运算，能够实现O(nlogn)的复杂度.此外，利用多项式可以表示集合元素.具体来说，给定一个集合，可以将集合元素作为多项式零点值来生成代表集合的多项式，那么2个多项式的最大公约多项式为集合交集，而2个多项式相乘则代表了集合并集.因此，集合求交问题可以转换成针对多项式的运算；Kissner和Song[15]基于此想法构造了针对集合操作的隐私保护协议，包括集合求交、交集大小、门限并集等.

除了计算集合交集，很多时候参与方可能只想计算关于交集的某个函数f(X∩Y)，比如保密计算交集大小、交集元素权重求和、求方差等交集统计量.文献[16]中的协议可以计算集合交集大小.文献[17]基于加同态加密设计了保密交集求和协议，可以应用到计算广告转化率协议中.具体来说，该协议假设参与方P0持有集合X，另一个参与方P1不仅持有集合Y，同时对于Y中的每一个元素都有一个对应的权值，记该权值集合为V.双方执行交集权值求和协议，最终P0得到所有交集元素的权值和.随后，Miao等人[18]利用零知识证明对文献[16]的交集求和协议进行了安全加固，能够实现双输出模式的恶意敌手下安全.之前提到的文献[6]同样支持计算交集的函数，该文献基于GMW范型[19]的通用电路构造了计算关于交集的某些函数，本质上能够计算关于交集的任何函数.然而，基于GMW范型的安全计算一个主要的缺点是轮数较高.此外，Le等人[20]基于三方秘密共享设计了一个两方计算集合交集函数的协议，然而，该协议需要额外借助一个第三方服务器，且服务器不能和任何任意一方合谋；文献[21]对集合求交的基本构造技巧进行了归纳和总结.

2 预备知识

本节中主要介绍后文用到的符号和安全多方计算的一些基本组件.

2.1 符号说明

本文中，λ表示安全参数，函数μ:N→R是可忽略函数，即对于任意大的正多项式ploy(·)以及任何足够大的λ，都有μ(λ)<1ploy(λ).

2.2 相关原语

1) 茫然传输(OT).OT是安全多方计算的核心组件.以应用最广泛的2选1 OT为例，发送者提供2个消息m0,m1,接收者提供选择比特b，最终接收者拿到mb.OT的安全性要求接收者不知道m1-b，而发送者不知道接收者的选择比特b.更一般地，可以定义N选1 OT，其中发送者提供N个消息，接收者只能拿到1个消息.OT的理想功能函数定义为：

FOT功能函数:

① 接收方提供输入(m1,m2,…,mN)，接收方输入选择比特b;

② 将mb发送给发送方.

OT只能通过公钥密码原语进行构造，但是可以利用对称技巧进行高效拓展.具体来说，OT拓展协议只需要执行少量的基础OT，附加高效的对称操作，就可以产生大量的拓展OT实例.当前，OT拓展技术已经相当高效.

2) 茫然伪随机函数.茫然伪随机函数(OPRF)是一个两方协议，其中发送方持有伪随机函数F的密钥key,而接收方持有输入x.双方执行协议后，接收方输出F(key,x)而发送方输出为空.OPRF的理想功能函数定义为：

FOPRF功能函数:

① 接收方提供输入(m1,m2,…,mt),随机选一个PRF密钥key;

② 将key发送给发送方，(F(key,m1),F(key,m2),…,F(key,mt))发送给接收方.

OPRF理想功能函数可通过多种方式实现，如通过两方计算AES电路来实现，其中发送方持有密钥key，接收方持有输入x，双方执行安全计算AES(key,x)，最终将安全计算结果揭示给OPRF接收方.此外，可利用专用协议计算F(key,x)=H(x,H′(x)key)，其中H是普通Hash函数，H′的输出为某个群元素.当然也可以利用文献[10]中的OPRF协议，该OPRF协议可以仅仅利用OT拓展协议来实现，因而其计算效率得到大大优化.在实际协议中，参与方可以根据具体场景的需求来选取合适的OPRF协议.为了描述简单，本文用理想功能函数FOPRF来代替具体的OPRF协议.

在布谷鸟Hash方案中，Hash表保存了b个桶B1,B2,…,Bb，布谷鸟Hash利用了2个Hash函数h1,h2:{0,1}σ→[1,b]将m个元素映射到b=2(1+ε)m个桶中.在布谷鸟Hash的元素插入过程中，当插入元素e时，首先利用2个Hash函数计算2个位置h1(e)和h2(e)，然后检查h1(e)和h2(e)哪一个位置空缺.如果有空缺，那么随机选一个空缺位置插入e.如果2个位置都已经存在元素，那么随机选一个位置，用e替换该位置原来的元素o.然后继续计算h1(o)和h2(o),对元素o继续做插入处理.持续以上过程，直到没有元素被移出或者移出次数达到某个界值.对于后一种情况，最后一个被移出的数据会被放置在缓存Stash中.现存结论[6-7]表明，当|Stash|≤lnm时，插入m个元素后失败的概率为m-s.布谷鸟Hash的查找非常高效，对于待查元素x，只需要计算h1(x)和h2(x)，然后查找b个桶中对应2个位置.如果元素x存在，必存在于h1(x)和h2(x)或者Stash中.

文献[6-7]设计了无Stash的布谷Hash.简单来说，通过增加布谷Hash函数个数(如Hash函数个数k设为3，4，5)以及合理设置桶的数目，可以在很大的概率下将所有元素放置在桶中，而无需Stash.这种无Stash的布谷Hash技巧，可以避免Stash中元素和集合Y的成员测试.在本文方案中，所有布谷Hash采用此类无Stash的布谷Hash构造技巧.

2.3 安全定义

本节回顾半诚实安全模型的定义，同时也是本文方案可以达到的安全属性.在半诚实安全模型中，参与方会诚实地参与协议执行，但好奇的腐化方会尝试分析协议交互视图来尝试学到额外(关于诚实方输入)的信息.

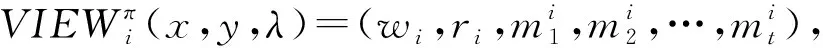
定义1.令f=(f0,f1)为待计算功能函数，方案π在半诚实敌手下安全计算了功能函数f，必须存在该路多项式时间的模拟器Si,i∈{0,1}，使得：

其中,x,y∈{0,1}*,|x|=|y|且λ∈N.

对于确定性的功能函数，由于f(x,y)=OUTPUTπ(x,y,λ)，定义1可以简化为

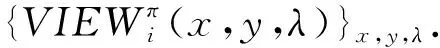
3 协议构造

本节介绍隐私保护的集合求交集大小、并集大小以及交集权值和、权值方差等隐私保护统计协议.

3.1 协议组件

3.1.1 共享等值比较

在一个共享等值比较协议中，参与方P0和P1各自提供输入x和y，协议运行结束后，双方共享等值比较结果e.其中，如果x=y,P0和P1共享比特e=1；否则，共享e=0.其功能函数为

FSEQ:

① 从P0收到x，从P1收到y;

② 如果x=y,e←1,否则e←0;

③ 随机选取r←Z2,发送r给P0,发送e⊕r给P1.

功能函数FSEQ可以通过YAO协议或者GMW协议计算等值比较电路来实现.然而，简单的基于电路的方法存在通信量或轮数过高的缺点.在本文中借助一个基于OT的等值比较协议ΠSEQ[23]来安全计算功能函数FSEQ，相比基于电路的实现，对于长度为l位的待比较字符串，该协议的轮数仅为O(log logl).

ΠSEQ:

① 令v←l,x(v)←x,y(v)←y;

② whilev>δ*δ最小可取为3*

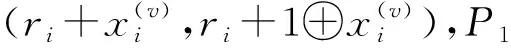
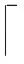
③ end while

④ 令N←2v,P0随机选取b←Z2,计算(m0,m1,…,mN-1)，其中mx(v)←b⊕1，而对于任意i≠x(v)，mi←b⊕1;

⑤P0和P1执行N选1 OT，P0输入(m0,m1,…,mN-1)，P1输入y(v).最终，P0输出b，P1输出my(v).

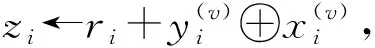
对于长度为l的初始输入，该协议仅需O(log logl)轮便可分享最终的等值比较结果.这意味着对于长度为128 b的字符串，参与方可以在3轮之内执行完该协议，而且每轮计算量相比于前一轮都大大缩减.此外，利用高效的OT拓展技术和OT预处理技术，协议的计算效率也是相当高效的.

定理1.在FOT混合模式下，协议ΠSEQ安全计算了功能函数FSEQ.

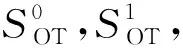
1)P0被腐化.模拟器S0需要根据输入输出(x，b)，模拟生成一个和真实协议不可区分的视图.令ΠSEQ中OT的调用次数为m+1,其中包括m次2选1 OT和1次N选1 OT.这里将构造m+1个中间视图，其中初始视图和最终视图分别为真实视图和模拟视图.需要证明任意2个相邻游戏的可区分概率为可忽略概率，因此最终得出真实视图和模拟试图不可区分的结论.

H0:H0的视图和真实协议的视图完全相同.

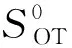
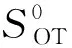
由以上游戏可知，H0为真实协议的视图，而Hm+1为最终模拟器构造的模拟视图.假如存在一个区分器D，能够以不可忽略的概率区分出H0和Hm+1.即：

|Pr[D(H0(x,y,r0))]-
Pr[D(Hm+1(x,y,r0))]|>1p(λ);

那么必定存在i，使得：

|Pr[D(Hi-1(x,y,r0))]-
Pr[D(Hi(x,y,r0))]|>1((m+1)p(λ)).

可见，可以利用以上方法构造一个针对第i次OT发送者模拟的区分器D.然而，这和OT的安全性是矛盾的.因此，区分器D对H0和Hm+1的区分优势是可忽略的.

2)P1被腐化.模拟器S1需要根据输入输出(y，my(v))，模拟生成一个和真实协议执行不可区分的视图.类似于证明P0被腐化的情况，令ΠSEQ中OT的调用次数为m+1,其中包括m次2选1 OT和1次N选1 OT.将构造m+1个中间视图，其中初始视图和最终视图分别为真实视图和模拟视图.需要证明使得任意2个相邻游戏的可区分概率为可忽略，从而最终得出真实视图和模拟试图不可区分的结论.

H0:H0的视图和真实协议的视图完全相同.

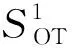
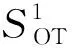
由以上游戏可知，H0为真实协议的视图，而Hm+1为最终模拟器构造的模拟视图.假如存在一个区分器D，能够以不可忽略的概率区分出H0和Hm+1.即：

|Pr[D(H0(x,y,r0))]-
Pr[D(Hm+1(x,y,r0))]|>1p(λ);

那么必定存在i，使得：

|Pr[D(Hi-1(x,y,r0))]-
Pr[D(Hi(x,y,r0))]|>1((m+1)p(λ)).

类似于之前的证明，可以利用以上方法构造针对第i次OT接收者模拟视图的区分器D.然而，这和OT的安全性是矛盾的.因此，区分器D对H0和Hm+1的区分优势是可忽略的.

证毕.

3.1.2 共享成员测试

成员测试关注以下场景：P0持有元素x,P1持有集合Y,P0想测试元素x是否属于P1的集合Y.针对本文关注的场景，要求成员测试的结果共享在参与方，而任意一方不知道测试结果.为此，定义共享成员测试理想功能函数FSPMT：

FSPMT功能函数：

①P0输入元素x，P1输入集合Y;

② 计算成员测试结果c,如果x∈Y，则c←1,否则c←0;

③ 随机选取r←Z2,发送r给P0,发送c⊕r给P1.

针对该理想功能函数，给出了一个计算FSPMT的协议ΠSPMT，该协议利用了功能函数FOPRF和FSEQ，因此工作在(FOPRF,FSEQ)-混合模式.

ΠSPMT:

①P0作为FOPRF的接收方，输入x.P1作为FOPRF的发送方.最终，FOPRF发送伪随机函数F的密钥key给P1，发送F(key,x)给P0;

② 针对任yi∈Y，其中i∈[1,|Y|],P1随机选取r←Fp，计算多项式：

P1发送多项式P的系数给P0;

③P0计算s=P(F(key,x)).2个参与方调用FSEQ，其中P0输入s，P1输入r.最终参与方共享r和s的等值关系.

通过协议ΠSPMT，参与方首先调用FOPRF使得P0拿到OPRF输出F(key,x).随后，P1生成多项式P(x)并将多项式的系数发送给P0.这里的直觉是，如果x∈Y，那么x必定是P(x)-r的某个零点值，那么P0计算s=P(F(key,x))必定和r相等.因此，对s和r调用共享等值功能函数FSEQ，最终将x是否属于Y的信息共享到2个参与方.

ΠSPMT协议利用了功能函数FOPRF和FSEQ，其中FSEQ可以利用基于OT拓展的OPRF实现[9]，或者基于茫然伪随机函数F(key,x)=H(x,H′(x)key)实现.P1生成多项式P(x)并将多项式的系数发送给P0，该过程需要发送的系数规模和集合大小|Y|相当.最终的等值比较功能函数由协议ΠSEQ实现，轮数为O(log logl).

定理2.在(FOPRF，FSEQ)-混合模式下，协议ΠSEQ安全计算了功能函数FSPMT.

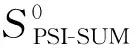
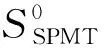
H0:H0的视图和真实协议的视图完全相同.

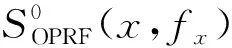
H2:H2的视图和H1的视图相同，除了模拟器随机选取多项式系数.由于密钥只有多项式生成方知道，因此随机生成的P*的多项式系数和真实协议接收得到的参数不可区分.因此，H1和H2的视图无法区分.

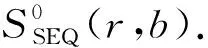
证毕.

3.2 具体方案

协议ΠSPMT只是针对P0持有一个元素，而P1持有集合Y的情况.而本文关注P0持有集合X，P1持有集合Y，双方计算f(X∩Y)的情况.如果重复调用以上协议|X|次，会带来O(n2)的通信复杂度.

针对这个问题，同以往的PSI方案一样，采用Hash技巧降低上述协议的复杂度.具体来说，P0利用布谷Hash将其输入集合X映射到Hash表中，而P1利用普通Hash，将每个元素y∈Y放置到Hash表中的所有可能位置.布谷Hash的性质保证如果P0的某个元素x∈Yi，那么无论x被放在所有可能位置的哪一个位置i，在那个位置i上必有x∈Yi，其中Yi是P1利用简单Hash映射到位置i的所有元素.在接下来的协议中将阐述具体操作过程.

给定功能函数FSPMT，辅助以特定的Hash技巧，可以很方便地计算集合交集大小、交集权值和、方差等基于集合的统计计算.具体示意图如图1所示.

3.2.1 计算交集权值和

FPSI-SUM功能函数：

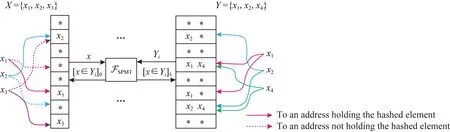
Fig. 1 Private shared membership test based on cuckoo hashing图1 基于布谷Hash的共享成员测试示意图

①P0输入X以及权值集合V，P1输入集合Y;

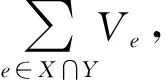
针对该理想功能函数，设计了计算交集权值和的协议ΠPSI-SUM，利用3.1节中共享等值比较协议和OT来安全实现FPSI-SUM.

ΠPSI-SUM:

输入：P0输入集合X以及每个元素的权值集合V，P1输入集合Y，其中|X|=|Y|=O(n)，以及共享布谷Hash桶个数m=k(1+ε)n，其中k是某个常数值；

①P0利用布谷Hash将X映射到Hash表B1,B2,…,Bm中，令桶i中的元素为xi.P1利用简单Hash，将集合Y映射到m个桶中，其中每个桶中的元素们定义为Yi.

② 参与方对逐桶执行协议ΠSPMT.P0输入xi，P1输入Yi，参与方共享xi是否属于Yi的信息ci.最终P0输出[ci]0，P1输出[ci]1，其中ci=[ci]1⊕[ci]0.

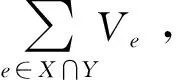
以上方案可以很方便地计算交集和并集权值大小.针对交集大小，发送者只需将每个元素对应的权值统一设置为1即可，这样只有在交集中的元素被计数为1，否则为0.此外，由于并集大小可以通过公式|X∪Y|=|X|+|Y|-|X∩Y|求得.给定共享的交集大小，只需要计算加法(加法在安全计算中不需要交互就可完成)，可以很高效地计算得到并集大小.ΠPSI-SUM支持交集、并集大小计算，本文把以上2个协议特别地记为ΠPSI-CA和ΠPSU-CA.

针对更一般的情况，ΠPSI-SUM可以用于计算广告转化率.在计算广告转化率协议中，广告投放商拥有访问广告的用户集合，用户点击广告后，可能会转向零售商购买商品.因此，零售商不仅拥有购买商品的用户集合，还额外拥有用户的消费金额.广告商和零售商想要计算所有交集用户的消费总和.可见，计算广告转化率本质上是求交集用户的消费之和，因而可以通过协议ΠPSI-SUM解决.文献[17-18]中的方案可以实现以上计算需求，然而，这些协议需要额外泄露交集大小，并且严重依赖公钥密码.本方案不需要泄露交集大小，并且仅仅需要OT就可以实现计算需求.考虑到当下高效的OT拓展和OT预处理技术，本方案的计算效率更加高效.

定理3.在(FSPMT,FOT)-混合模式下，协议ΠPSI-SUM安全计算了功能函数FPSI-SUM.

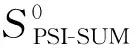
H0:H0的视图和真实协议的视图完全相同.

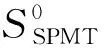
H2:H2的视图和H1的视图相同，除了模拟器调用OT模拟器来生成OT发送过程中的视图.由OT的安全性，H1和H2的视图无法区分.

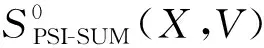
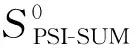
证毕.

3.2.2 计算交集权值的方差

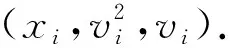
4 效率分析

共享成员测试作为本文的最重要的支撑协议，其效率影响着后续基于交集函数的协议的效率.因此，本节主要分析共享成员测试协议的轮数、计算和通信效率，以及和相关方案的比较.

1) 轮数复杂度.共享成员测试协议主要包含OPRF协议、多项式构造、共享等值比较协议.其中OPRF协议根据具体实现不同，轮数会有相应的区别.基于OT拓展的OPRF协议需要执行一轮的基础OT然后本地生成OPRF输出，加上利用OT拓展协议中的接收矩阵生成多项式并传输系数，总共需要2轮.随后，基于OT的共享等值比较协议中，针对长度为l的待比较字符串，仅需要O(log logl)轮复杂度即可完成计算.在通常l=64的设定下，这意味着至多需要3轮即可完成等值比较运算.而通常基于GMW范型的等值比较电路的构造，需要O(logl)轮完成计算.从渐进意义上来说，协议的论复杂度为O(log logl),具体轮越数为5轮.而基于电路的构造，渐进意义下至少为O(logl),在l=64的具体参数下，轮数约为10轮.

2) 计算复杂度.本方案不需要同态加密或者通用的电路构造得到，而是高度依赖OT.要知道，执行O(n)次OT，其中n≫λ，可以通过仅仅执行O(λ)次的基础OT协议(基础OT协议需要公钥操作)，附加高效O(n)次对称操作，因而可以非常高效地生成大量OT实例.从这个意义上讲，相比于依赖同态加密的构造[17]和通用电路的构造[6]，本方案计算效率更有优势.此外，P1的Hash表中每个桶的元素数量最多为O(logn)，利用简单的多项式计算方法需要O(logn)，总共O(nlogn).

3) 通信复杂度.在共享成员测试协议中，参与方逐桶执行协议.其中P1利用简单Hash将集合Y分配到规模为O(n)的Hash表中，其中每个桶的元素个数最多为O(logn).由于P1发送的多项式系数个数和桶中的元素个数相等，所以执行所有桶的成员测试协议总共需要O(nlogn)的通信量.对于共享等值比较协议，一次l位字符串的比较，通信量为O(l).而在实际情况下n≫λ，因此总体的通信复杂度为O(nlogn).为了进一步降低通信量，可采用文献[6]中多项式插值的技巧，将通信复杂度降低到O(n)，然而该优化需改变多项式计算方法，一定程度上牺牲了部分计算效率.是否接受该优化，取决于协议应用的具体场景.

目前能够两方计算(不依赖第三方服务器)交集函数的集合求交方案中，最高效的方案是基于电路的构造[6].和其相比，本方案在轮复杂度上更具优势.具体信息如表1所示：

Table 1 Comparison of Efficiency

5 结束语

保密集合求交是很重要的隐私保护数据处理协议，具有实际的商业应用前景.本文仅利用茫然传输，设计了一组支持计算集合交集函数的协议，能够在不泄露交集元素的前提下，计算集合交集大小、并集大小以及交集权值和、交集权值方差.利用Hash技巧，对协议的通信量进行了优化.协议可以在半诚实敌手下证明安全.在未来，将探索支持更多统计功能的协议，以及将这些协议应用到具体的应用场景中.