利用液晶波片去除零级像的数字全息成像研究

宋洁睿， 孙 蕾， 吴 玥， 袁子怡， 董 昊， 孔 勇

（上海工程技术大学 电子电气学院， 上海201620）

0 引 言

数字全息技术（DH），是一种既能记录振幅图像又能记录相位图像的方式，可对物体图像目标进行实时三维检测和测量［1］。 此外，即使样品焦点不在最佳位置，或者光学系统包含像差，DH 也能够重建目标波的振幅和相位［2-3］。 基于这些优点，DH 在工业和科学领域得到广泛的应用，特别是在生物医学领域，实时监测活细胞的振幅和相位图像［4］。 在工业产品制造中，通过对产品进行地形和断层的实时检测，可以显著提高生产能力。

对物光和参考光干涉形成全息图，再进行数字再现或光学再现的过程中，在成像平面中会出现零级像、原始像和共轭像。 其中零级像位于成像平面的中心，具有较高的能量，形成零级亮斑。 它会严重影响再现像的成像质量，导致原始像或共轭像不清晰，降低成像的信噪比，再现图像细节较难分辨。 因此，去除再现平面中心的零级亮斑尤为重要。 目前，常用的几种消除零级像的方法主要包括频谱滤波［5］、空域滤波法［6-7］、相移法［8-11］等。 频域滤波法虽能够有效地去除零级像的干扰，提高原始像或共轭像的对比度，但普遍存在滤波窗口选择困难且主观性强等问题。 基于空间域的滤波方法由于计算简单，只需记录一幅全息图，适于动态探测而被广泛应用于数字全息中。 但空域均值滤波方法在滤波模板的尺寸较大时，计算速度较慢，且采用均值滤波时物体的细节变得模糊；空域有限脉冲响应滤波器在有限脉冲响应滤波后，会减弱再现像的强度。 利用相移的方式也可以很好的去除直流和共轭分量，但PZT 和波片相移全息系统具有结构复杂，响应速度较慢等缺点，而液晶空间调制器相移全息系统成本较高。 近期有人提出，采用循环迭代算法［12］和非线性滤波［13-14］等方法来消除零级衍射分量的影响，取得了较好的效果。 但迭代算法需要较长的运算时间，并且结果受初始条件影响。 非线性滤波方法仅局限于1／4 象限频谱区域内使用，而且需要在傅里叶频谱区域设置滤波窗口。

基于上述研究，本文提出利用电控液晶波片，在参考光路中引入任意相移δ 记录两次全息图，来实现提取离轴DH 中的物体信息。 一次任意相移法可有效的消除零级项的干扰，不需要零级项和物体信息完全分离也可以实现物体信息的再现。 此系统操作简易，只需通过控制电压使得液晶波片产生一次任意相移，不需要其他的硬件操作和精确的相移控制，稳定性较高。 此外，还具有成本低、响应速度快、结构简单等优点。

1 实验原理

1.1 一次任意相移法原理

离轴数字全息记录光学系统如图1 所示。 其中，O 和R 分别是物光及参考光，T 是电控液晶波片，P 是是生成参考光的棱镜，平面H 是全息记录面。

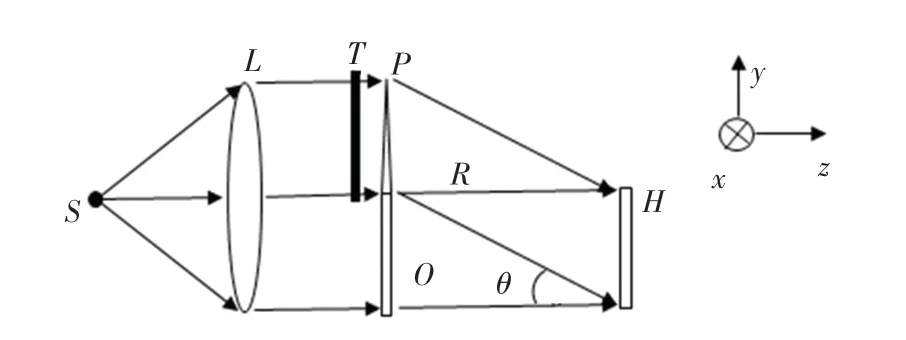
图1 离轴数字全息光学系统Fig. 1 Off-axis digital holographic optical system

再全息面上的参考光波可表示为：

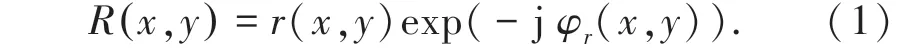
其中，r（x，y） 和φr（x，y） 分别为参考光光波的振幅和相位分布。 同理，全息面的物光波可表示为：

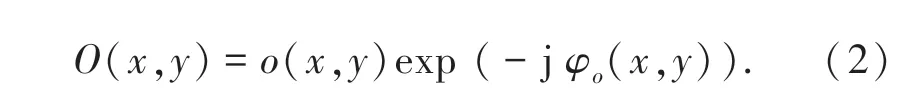
其中，o（x，y） 和φo（x，y） 分别为物光光波的振幅和相位分布。 则这两个波在全息面上的叠加复振幅是：

该光强用CMOS 相机记录下来，输入到计算机得到数字全息图：

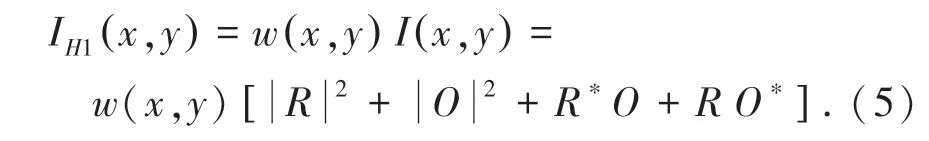
其中，w（x，y） 是CMOS 光电转换的窗口函数。对全息图进行再现后，前两项的直透光和晕轮光形成的零级像；第三项含有物体信息，形成原始像；第四项携带物体共轭信息，形成共轭像。 重建的图像中零级像和共轭像将对物体的原始像产生干扰，若在参考光路中加入电控液晶波片T，引入一相移δ 再次记录一幅全息图，即将参考光变为：

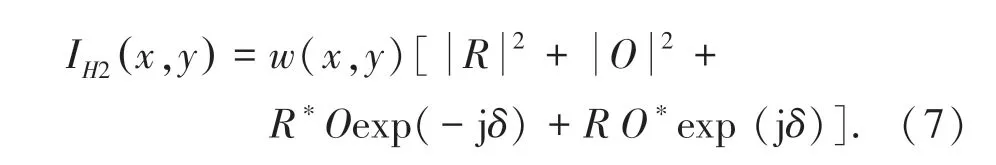
将两次记录的全息图相减可以得到不含零级项的全息图：

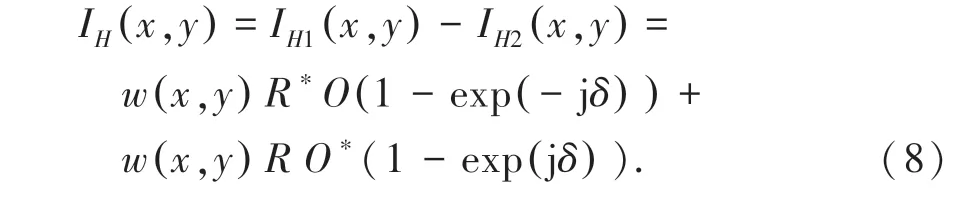
再次对全息图进行再现后，可以得到不含零级像的再现像。

1.2 电控液晶移相原理

液晶分子结构是非对称的，具有各向异形，通过控制液晶上的o 光及e 光折射率可以实现相位调制。

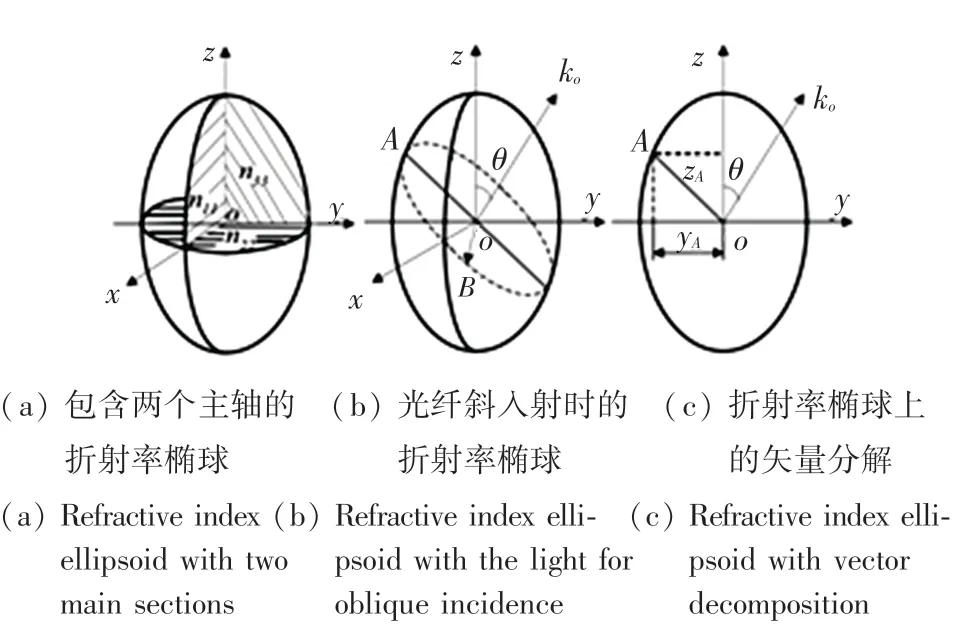
图2 向列型液晶折射率椭球Fig. 2 Ellipsoid of refractive index of nematic liquid crystal

如图2 所示，光线沿k0方向传播并与z 轴成θ角，通过原点作以k0为法线方向的平面， 得到一个与椭球相截后的椭圆。 OA 和OB 是椭圆两个主轴，两个主轴方向也被k0所允许存在的线偏振光矢量D方向。 OA 和OB 的矢径长度分别为这两个方向线偏振光的折射率。 因OB 方向永远保持和z 轴垂直，其矢径长度恒定为n⊥，而且不随θ 角变化而改变。 因此，沿OB 方向的光确定为寻常光o 光。 然而，OA 矢径长度在zoy 面内随θ 角变化而改变，沿OA 方向的光确定为非寻常光e 光。 要确定e 光的折射率，必须确定OA 矢径长度。 当zoy 平面跟折射率椭球相截时，可以得到：

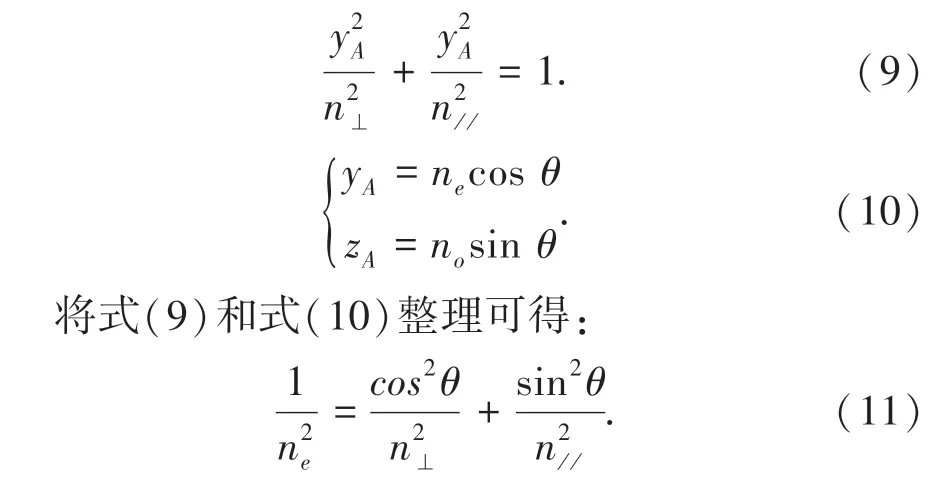
当液晶的各向异性发生双折射后，折射率可以表示为：

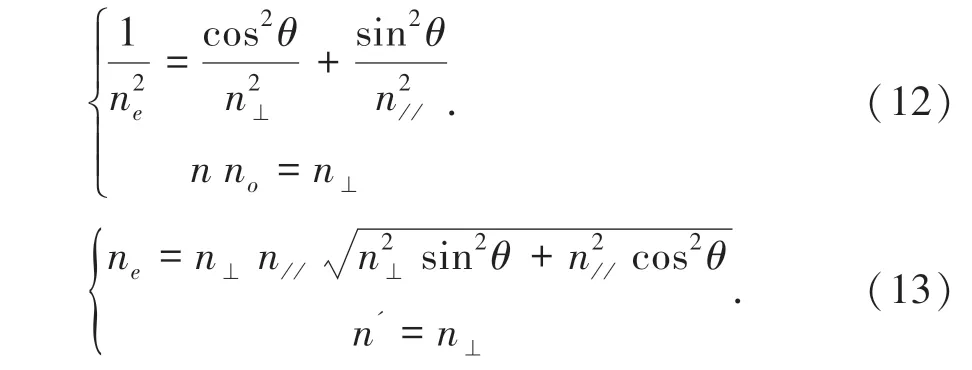
由式（13）可以分析入射向列型液晶的出射o 光和e 光的折射率。 当外界施加电压后，液晶指向发生改变，导致液晶对e 光的折射率发生改变，使液晶的双折射率改变，如式（14）：

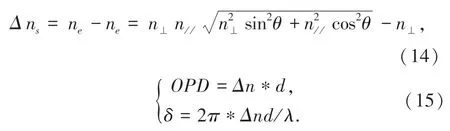
当有光射入液晶后，输出的o 光与e 光产生光程差OPD，如式（15）。 可以得到相位延迟，通过液晶电控双折射效应实现对光的相位调制。

液晶波片的琼斯矩阵为［15］：

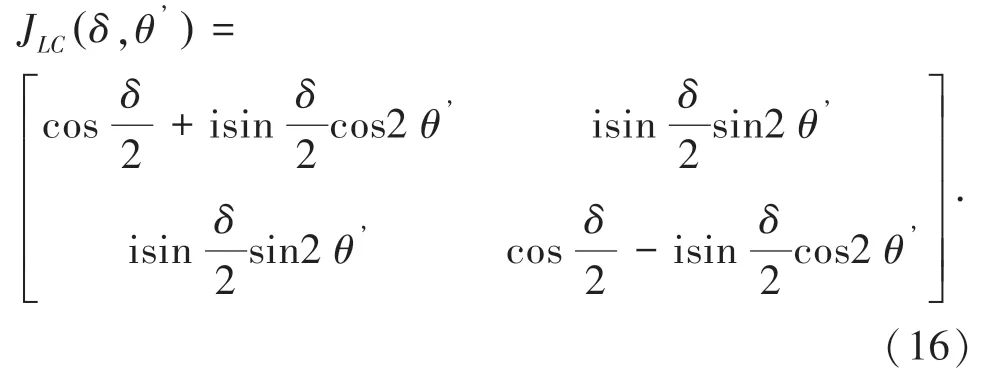
式中，θ’ 是液晶慢轴与x 轴夹角，当θ ＝90°，入射激光为平行于x 轴的线偏振光时，液晶输出的琼斯矩阵为［15］：

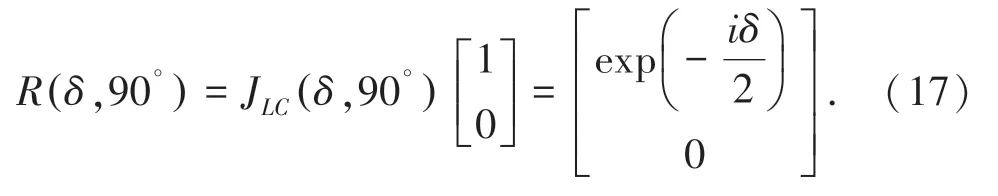
由此可见，通过调节加在液晶波片上的电压来调节延迟。 如式（6），在参考光中引进了可调的相位，达到了移相的目的。

2 实验结果及分析

实验中采用离轴数字全息光路，如图3 所示。其中，激光器输出波长为532 nm（由长春新产业光电技术有限公司提供）；激光束经PBS 起偏后，通过分光镜BS 分为参考光和物光两路，参考光经过电控液晶波片T（该液晶波片为E7 向列相型，由深圳市中达瑞和科技有限公司提供）实现相移；经过滤波准直后，从反射镜M1 反射垂直入射到CMOS 上，物光经反射镜M2 反射照射物体，物体表面发生漫反射光与参考光在CMOS 成像面产生干涉，形成干涉全息图；CMOS（由德国Cinogy 公司提供）记录该全息图并输入到电脑中，CMOS 像素为1280×1022且每个像素大小为5.3×5.3 （μm）；拍摄实物为长宽高均为10 mm 的骰子，记录距离为0.38 m；参考光与物光的夹角为5°；BE1 和BE2 为参考光和物光的扩束透镜系统（由物镜、小孔光阑和准直透镜组成）。 实验光路实物如图4 所示。

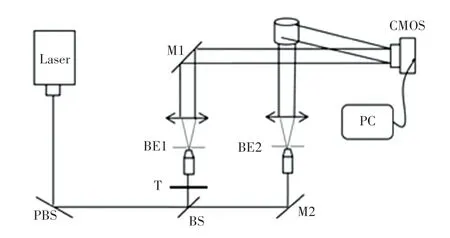
图3 离轴数字全息光路示意图Fig. 3 Schematic illustration of off-axis digital hologram

图4 实验光路图Fig. 4 Diagram of the experimental light path

首先，在液晶波片不加电压时记录一幅数字全息图，之后通过对液晶波片施加电压产生移相后再次纪录一幅全息图。 此过程仅通过电压改变了液晶波片的延迟量，而不需要进行其它机械操作，响应时间为10 ms 左右（如采用铁电相的液晶波片，响应时间可减小为100 μs 左右）［15］。 对记录的原始全息图进行菲涅尔再现，获得其频域图和再现像如图5所示。 其中图5（a）记录的是全息图。 图中横向和纵向的条纹是光路间激光来回反射所造成，可通过对全部光器件增加增透膜来降低。 图5（b）是全息图的频域信息。 可以看到零级项能量最高对物体信息有一定的干扰。 图5（c）是全息图的重建像，零级像衍射造成的干扰十分明显，因此在频域滤波再现。 图5（d）中图像信噪比较低，从而导致成像质量较差。

如在公式（8）中进行相移后，对两幅全息图进行处理得到的频域图和再现像，如图6 所示。 其中6（a）是处理后全息图的频域信息，可以明显的看到零级项得到很大程度的抑制。 相比图5（b），再现像（b）中的零级像产生的干扰大大降低。 因此，结合频域滤波再现图（c）的质量得到很大的提升。

从上述实验结果对比可以明显看到，零级项对物体信息有很大的干扰，频域中零级项占据大部分的能量，导致物体信息噪声较多。 本文提出的方法对于去除零级项的效果较为明显，在真实项被零级噪声淹没的条件下，仍可以较好的恢复出物体信息，使物体信息的质量得到很大的改善。 对于图6（b）中存在的少量残余直流分量，主要是对液晶两次相移前后外界的实验环境有所变化所造成，可采用维纳滤波［16］去噪和提高系统稳定性等方式来减小残余的直流分量。从图5（d）和图6（c）的对比中可以看出，虽然本文采用的是离轴全息成像系统，但实验的结果同样降低了直流分量对再现物理信噪比的影响。 所以，本文提出的去除直流分量的方式同样适用于同轴全息成像系统。

通过控制液晶固定的延迟量可以产生0，π／2，π和3／2π 等相移［17］，利用该结果可进行全息成像系统两步、三步和四步的移相研究，从而在共轭像的去除、四步相移去相位包裹、移相剪切散斑干涉成像等领域将会得到较好的应用。 由于本文采用的是向列相液晶，其响应时间为10 ms 左右，所以提出的该方案在实时三维全息的成像系统中也可以得到较好的应用。

3 结束语

本文通过电控液晶波片在参考光路中引入一次任意相移的方式，记录了两幅全息图。 此系统不需要进行额外的进行机械操作，有较好的稳定性，且对移相不需要精确的相位值，数据处理简单。 通过采用一次任意相移法结合频域滤波法，有效地消除了全息图中的零级干扰，得到了基本没有干扰的再现像，对图像的质量有较大的提升。 由于该方法可以直接消除零级项，所以也适应于记录相机分辨率较低、拍摄夹角较小的全息系统，而导致零级项和真实项重叠的情况也可以适用。 相信本文的结果将对实时三维成像的数字全息系统、等相关领域得到较好的应用。