基于改进烟花算法的多导弹目标分配方法*

安炳合，寇佳禹，王永骥，刘 磊

(1 华中科技大学人工智能与自动化学院， 武汉 430074；2 多谱信息处理技术国家级重点实验室， 武汉 430074)

0 引言

随着现代战争需求的提升，单一导弹对目标进行拦截已经难以满足作战要求。在多个目标需要被拦截的情况下，需要多个导弹协同作战。因此，在多导弹情况下的目标分配问题是作战过程中需要被解决的重要问题。在分配过程中需要考虑不同导弹对目标拦截的优势度，同时保证所有目标都被拦截，且不出现浪费火力的现象。已有不少学者对该问题进行了研究。

YANG F根据饱和攻击战术的思想，建立了武器-目标分配优化模型[1]，将火力分配决策与路径规划过程相结合，提出了一种在多火力和多约束条件下实现饱和攻击的方法。DOU J基于单舰空导弹射击区定义方法[2]，提出了编队舰空导弹系统的目标分配方法。王晓红基于目标的威胁度建立了一种目标分配模型[3]，采用匈牙利算法求解了分配问题。群体智能算法作为一种求解函数最优值的有效方法，也被广泛应用在目标分配问题中。针对火力分配问题，李平建立了一种层次分配结构[4]，把武器的作战效费比作为总的性能指标，利用遗传算法对性能指标进行了优化。周凌超在导弹与目标战术关系的基础上[5]，建立了多目标分配的数学模型，并提出一种改进的模拟退火算法对目标分配问题进行求解。黄峰首先改进了蚁群算法的搜索机制[6]，提出一种半约束随机蚁群算法，之后根据动态威胁因素，建立了防御过程的目标函数，利用改进的蚁群算法对多波次目标下的最优分配问题进行了求解。

在已有成果的基础上，针对多导弹拦截多目标情形下的目标分配问题，文中提出一种基于改进烟花算法的分配方法。首先综合考虑导弹的速度倾角，弹-目相对距离，弹-目速度关系对拦截效果的影响，建立了综合优势函数。之后将差分进化算法的交叉变异操作引入到烟花算法中，提出一种改进的烟花算法。对同一个标准函数，使用改进的烟花算法以及其他智能优化算法进行优化，仿真结果证明了改进后的算法具有更快的收敛速度。最后将提出的改进烟花算法用于求解目标分配问题，试验结果证明使用改进的烟花算法可以在较短的时间内完成目标分配任务。

1 多导弹目标分配建模

导弹与目标在平面内的相对运动模型如图1所示：其中M代表导弹，T代表目标，R代表导弹与目标的相对距离，VM为导弹的速度，VT为目标的速度，λ为视线角(LOS)，即导弹与目标的连线与基准线之间的夹角。导弹的导弹偏角为θM,目标的弹道偏角为θT，γ为导弹的速度前置角，即导弹速度方向与视线之间的夹角。

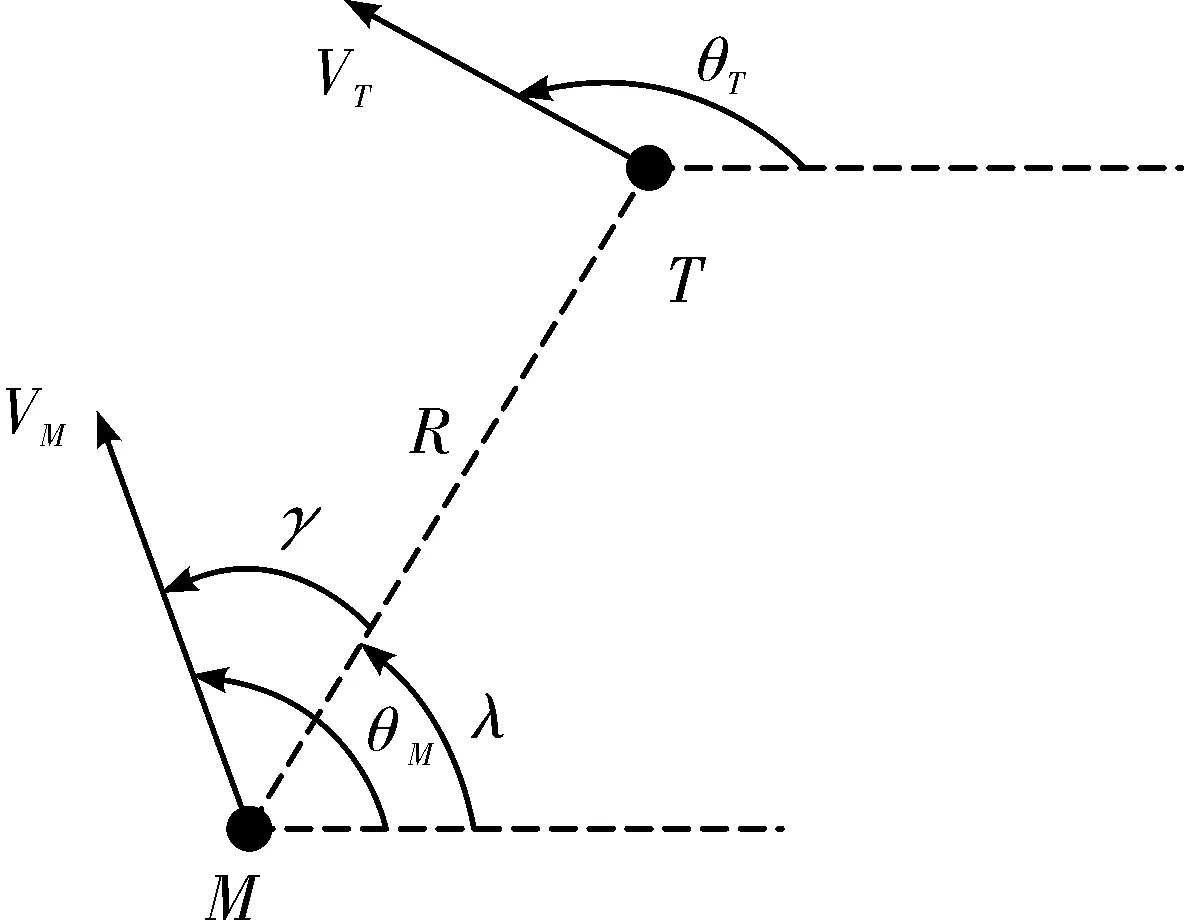
图1 导弹-目标相对运动示意图

根据几何关系可以得到：

γ=θM-λ

(1)

在多导弹进行目标拦截的过程中，需要进行合理的目标分配，获得最大的作战效能。同时在分配的过程中应保证所有目标都被拦截，且不存在过多导弹拦截同一目标的火力浪费现象。因此需要根据导弹的物理状态设计综合优势函数，保证分配的结果能使综合优势函数达到最大值,达到最优的拦截效能。在综合优势函数中主要需要考虑导弹的角度优势，导弹的距离优势以及导弹的速度优势对拦截过程的影响[7-8]。首先假设目标全部在导弹导引头的检测范围内，且多弹之间可以通过通讯网络相互通讯。

下面对各优势函数做具体分析：

1)导弹的角度优势

导弹速度方向沿视线方向的分量为VMcosγ，导弹速度沿视线方向的分量越大，越有利于导弹对目标的拦截，速度前置角γ的取值范围为[-π,π]，因此γ的绝对值越小，VMcosγ的值越大，当γ=0时，导弹可以获得最大的角度优势。根据以上分析定义如下的角度优势函数：

(2)

随着|γ|的增大，角度优势Sγ逐渐减小，符合实际物理意义。

2)导弹的距离优势

当目标进入导弹的导引头检测范围时，相对距离越小，越有利于拦截。因此定义距离优势函数：

(3)

其中：a为当前状态下所有导弹与不同目标间距离的最大值。 设计的距离优势函数随着距离的增大而减小。

3)导弹的速度优势

在一般情况下，提高导弹的速度更有利于对目标的拦截，因此定义速度优势函数：

(4)

在实际交战过程中，当导弹的距离优势与速度优势较大，但角度优势较小，即导弹的速度沿视线分量较小时，综合优势函数也不会很大[7]。考虑以上特性，采用综合优势函数：

s=M(c1sγsR+c2sγsV)

(5)

综合优势函数由两部分组成，角度优势与距离优势的乘积项以及角度优势与速度优势的乘积项。其中：M>0为正常数，c1、c2为两部分的权重因子，满足条件c1>0,c2>0, 且c1+c2=1 。

设在交战过程中，有i个导弹执行拦截任务，有j个目标需要被拦截，根据定义的综合优势函数可以计算出综合优势函数矩阵S为：

式中：si,j表示第i个导弹对第j个目标的综合优势函数值。

定义拦截矩阵D为：

式中：di,j的取值范围为{0,1}，当di,j=1 时代表第i个导弹对第j个目标进行拦截，当di,j=0时代表第i个导弹不对第j个目标进行拦截。为保证每一个导弹对应一个目标，且每一个目标都被拦截到，应满足条件：

(6)

(7)

为了避免出现过多导弹拦截同一目标造成火力浪费的现象，加入限制条件：

(8)

式中：G为针对同一目标的最大拦截弹数。

根据以上分析，可以将目标分配问题转化成含有约束的非线性整数规划问题：

(9)

约束条件为:

(10)

(11)

群体智能算法是求解非线性规划问题的有效手段，相较于传统的求解方法，在求解空间较大时具有较大的优势，同时不需要函数的梯度信息，更有利于实际应用。因此提出一种改进的烟花算法并应用改进的烟花算法求解目标分配问题。

2 改进的烟花算法设计

烟花算法是学者TAN Y提出的一种新型群体智能优化算法，它启发于烟花的爆炸过程[9]，在搜索最优解的过程中，以烟花的火花作为问题的可行解，模拟烟花爆炸产生新的火花的方式在旧的可行解的基础上产生新的可行解，并根据可行解的适应度函数(即待优化函数)进行选择，直到找到问题的最优解。但是，传统的烟花算法中种群内部的烟花粒子之间无法进行有效的信息交流：为了充分利用烟花粒子中所包含的可行解信息，文中在传统烟花算法的基础上引入差分进化算法中的交叉、变异操作，加强了粒子间的信息交流，提高算法的全局搜索能力。改进后的算法的流程如下：

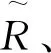
步骤2：爆炸。以第i个烟花粒子xi为例进行说明：根据其适应度函数值f(xi)分别按照式(12)、式(13)计算该烟花爆炸产生的火花数量Ni以及爆炸半径Ri。

(12)

(13)

式中：fmax和fmin分别代表所有烟花粒子中适应度函数值的最大值和最小值，ε是一个很小的常数，用来避免分子被零除。由式(12)、式(13)可知，当烟花粒子的适应度越好，即f(xi)越小时，该烟花粒子的爆炸半径越小，爆炸数目越多。采用这样的爆炸策略有利于在适应度较优的粒子附近寻找到最优解。

为了防止爆炸产生的火花数目过多或者过少，采用式(14)所示的策略对Ni进行限制。

(14)

假设烟花的维数为E，然后在每个即将爆炸的烟花xi中随机抽取一些维度k(1≤k≤rand(0,1)·E)，并采用式(15)所示的策略对爆炸产生火花的每一维位置进行计算。

(15)

式中：xi,j为烟花xi爆炸产生的第j(1≤j≤Ni)个火花。根据式(15)即可计算所有烟花爆炸产生火花的每一维位置。

假若爆炸产生火花的第k维度的值超出了可行域[xlow,xup]，则采用式(16)所示取模的方法将其映射到可行域内。

(16)

最后对所有爆炸产生的火花计算其各自的适应度函数值。

步骤3：差分变异。借鉴差分进化算法中交叉、变异的操作[10]，产生一定数量的变异火花。首先在当前种群内部任意选取4个不同的个体Q1、Q2、Q3、Q4以及适应度最优个体Qbest，按照式(17)的计算方式交叉产生第i个变异火花Ui，F为缩放因子。

Ui=Qbest+F·(Q1-Q2)+F·(Q3-Q4)

(17)

然后在种群内部随机选取一个未选择过的烟花或火花粒子Qi，并按照所设定的交叉率CR对粒子Ui中的第j维信息进行变异操作，产生式(18)所示的最终变异火花Ui，并计算其适应度函数值。

(18)

步骤4：选择。首先选取当前种群(包括烟花、子代火花、变异火花)中适应度最优的个体参与下一次迭代，然后采用轮盘赌的方式在其余的所有个体中选取参与下一次迭代的其余个体。每个体被选中的概率采用式(19)所示的策略进行计算。

(19)

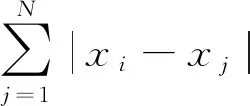
步骤5：判断。若算法已达到最大迭代次数或者最优解满足所需要求则结束迭代寻优过程。反之，跳至步骤2继续循环迭代寻优。

整个改进烟花算法的流程如图2所示。

3 数值仿真

3.1 改进烟花算法性能测试

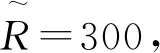
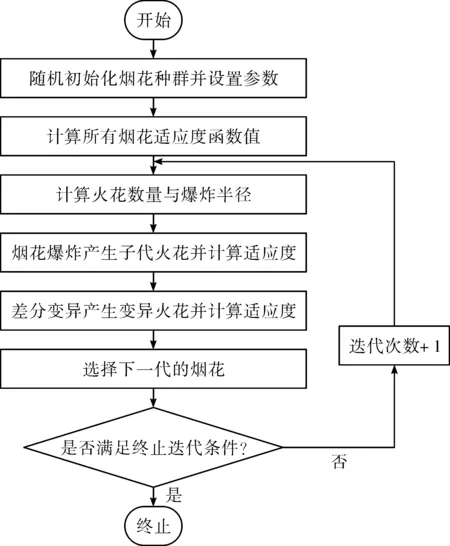
图2 改进烟花算法流程图

1)标准测试函数Beale 函数如式(20)所示。

J1(x,y)=(1.5-x+xy)2+(2.25-x+xy2)2+

(2.625-x+xy3)2

(20)

J1(x,y)在其定义域x∈[-4.5, 4.5],y∈[-4.5, 4.5] 内是一个多模态函数，存在多个极小值点，全局最小值点为J1(3,0.5)=0。其函数图像如图3所示，使用上述3种优化算法搜索函数的最小值，仿真结果如图4所示。

图3 Beale函数图像

根据适应度变化曲线可以看出，使用改进后的烟花算法收敛速度更快，认为当适应度函数的值小于1×10-4时，优化算法已经找到最优解。使用传统烟花算法找到最优解需要的迭代次数为20次，使用改进的烟花算法需要6次，使用差分进化算法需要28次，改进的烟花算法需要的次数最少，证明了改进烟花算法具有较好的收敛性。

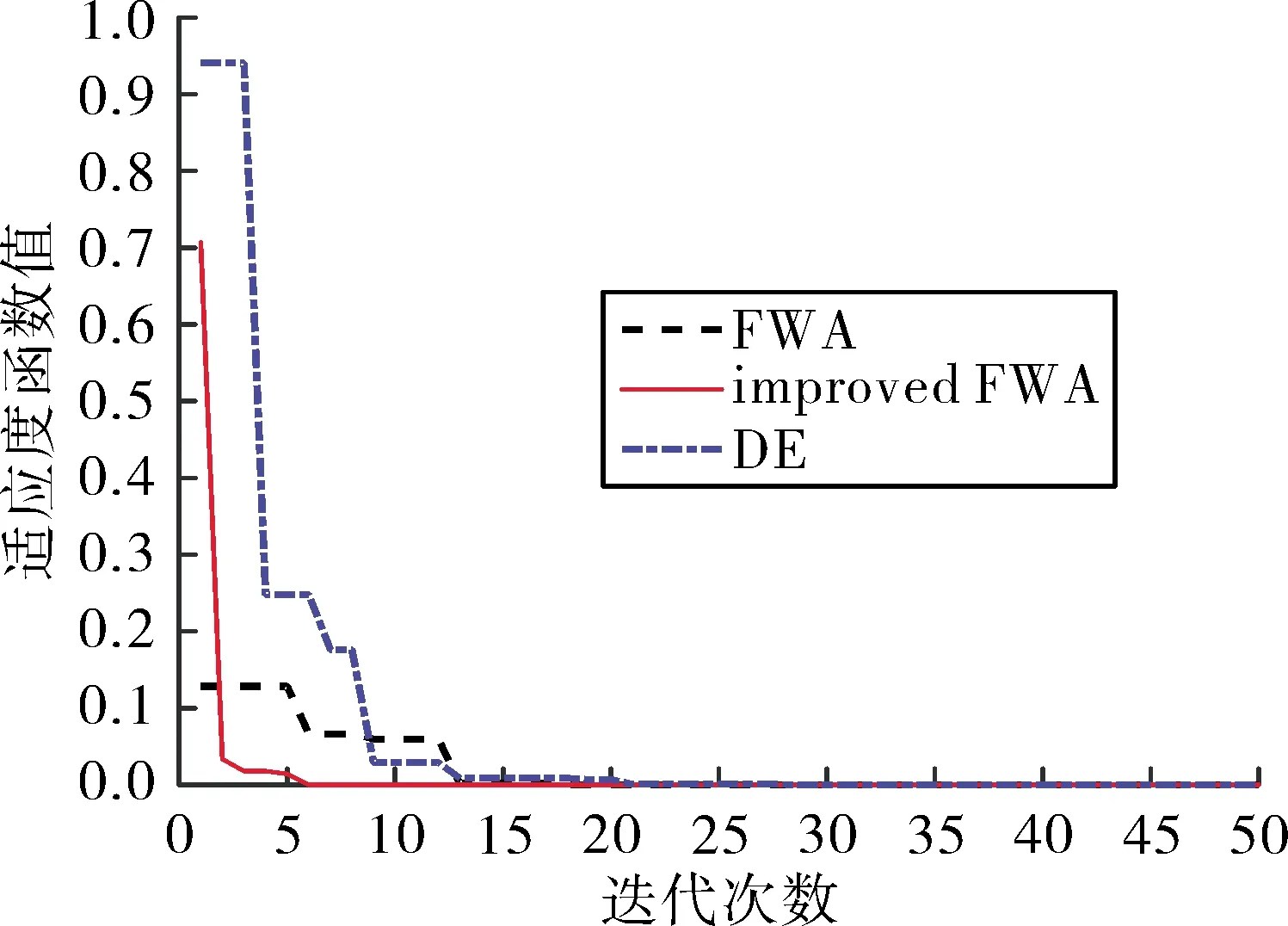
图4 适应度函数变化曲线

2)标准测试函数Eggholder 函数如式(21)所示。

(21)

J2(x,y)在其定义域x∈[-512, 512],y∈[-512, 512] 内存在众多极小值点，其函数图像如图5所示，函数的全局最小值点为J1(512,404.2319)=-959.6407。使用上述3种优化算法搜索函数的最小值，仿真结果如图6所示。

图5 Eggholder 函数图像

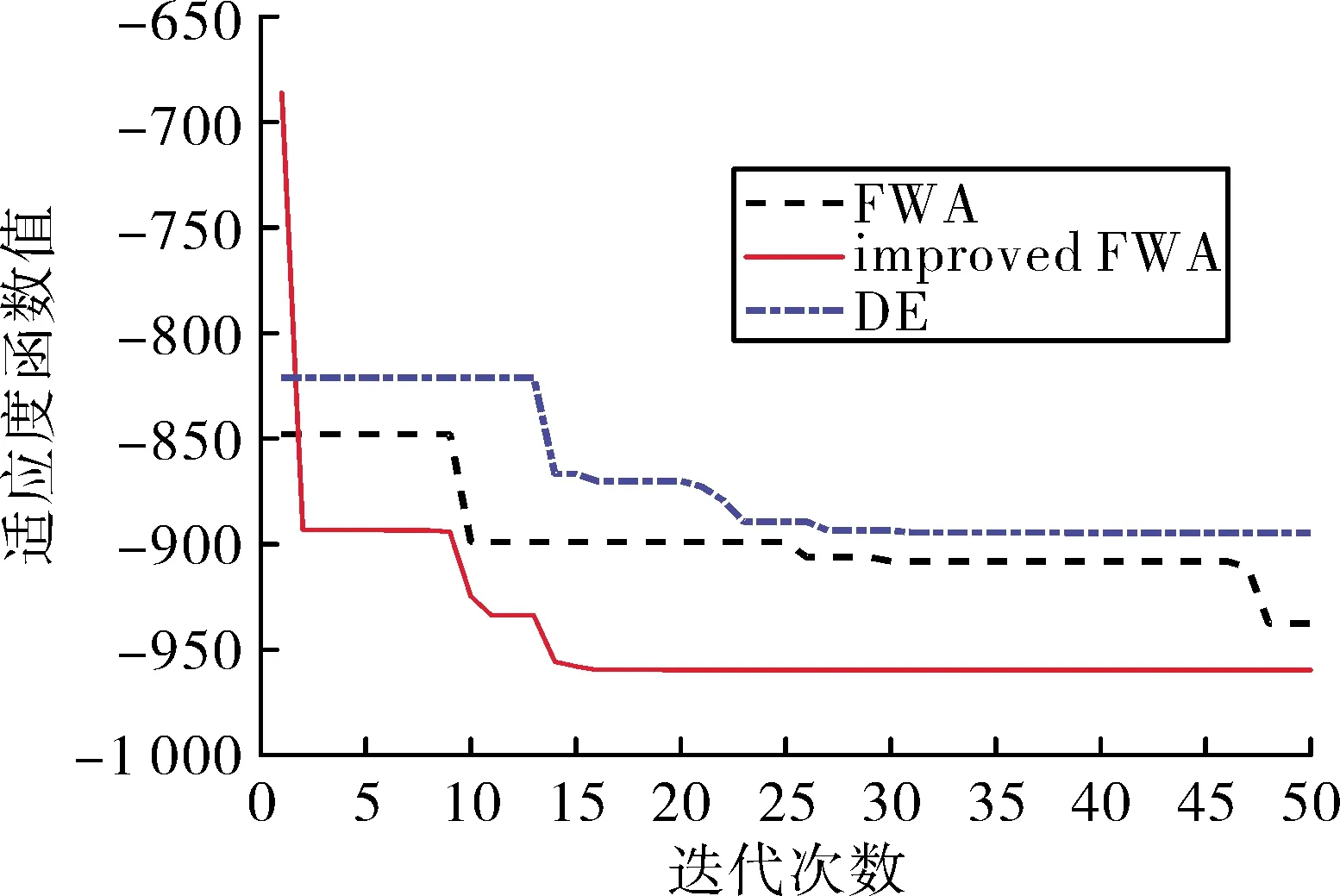
图6 适应度函数变化曲线

根据适应度变化曲线可以看出，使用改进后的烟花算法，达到最大迭代次数后，使用改进的烟花算法已经找到了全局最优解，且收敛速度较快，最终使用传统烟花算法搜索的结果为J2(507.8374,398.3313)=-937.489，使用差分进化算法搜索的结果为J2(-465.7,385.7107)=-894.579，使用改进烟花算法搜索到的最优解为：J2(512,404.2131)=-959.640，由仿真结果可以看出使用改进烟花算法优化得到的解更接近真实最小值点，证明改进后的烟花算法具有更好的全局搜索能力。

3.2 使用改进的烟花算法求解目标分配问题

设执行拦截任务的导弹共有6个，需要被拦截的目标为4个，每一代火花数目选取为10个，导弹的位置与目标位置如表1所示，导弹的速度均为300 m/s,目标的速度为150 m/s,导弹的弹道偏角均为0° 。综合优势函数的参数取值为c1=0.5,c2=0.5,M=5,G=2。根据当前交战状态以及式(5)可以计算出当前综合优势函数矩阵S，之后采用改进的烟花算法对分配方案进行优化。改进烟花算法参数的设置与3.1节相同。

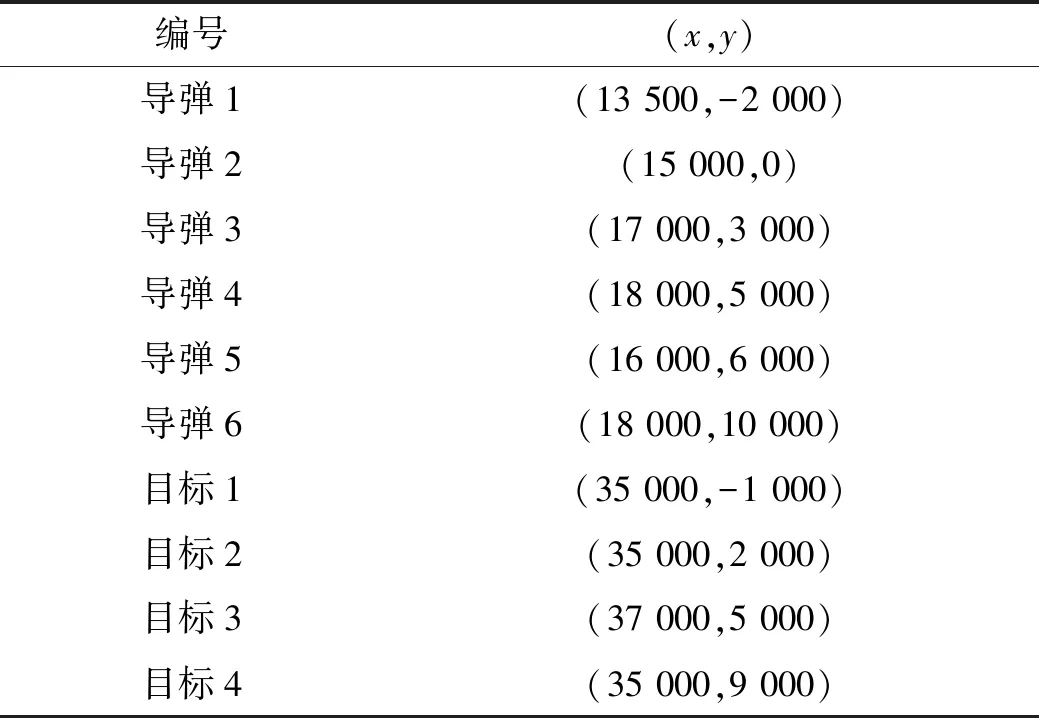
表1 导弹与目标位置分布 m

烟花粒子采用如图7所示的方式编码：每一个烟花粒子共6维，第k(k=1～6)维的取值代表第k枚导弹拦截的目标序号，按此方式编码可满足一枚导弹只拦截1个目标的约束。在烟花算法的迭代过程中，检测粒子是否满足约束式(11)，如不满足则该烟花粒子的综合优势函数直接取0值。优化过程适应度函数变化曲线如图8所示，最终目标分配结果如图9所示。

图7 烟花粒子的编码方式

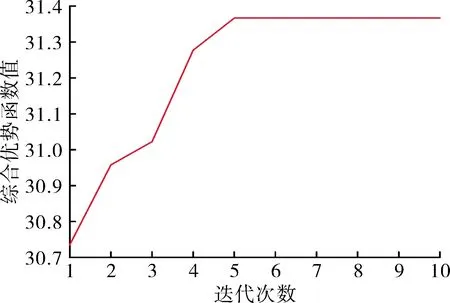
图8 综合优势函数变化曲线

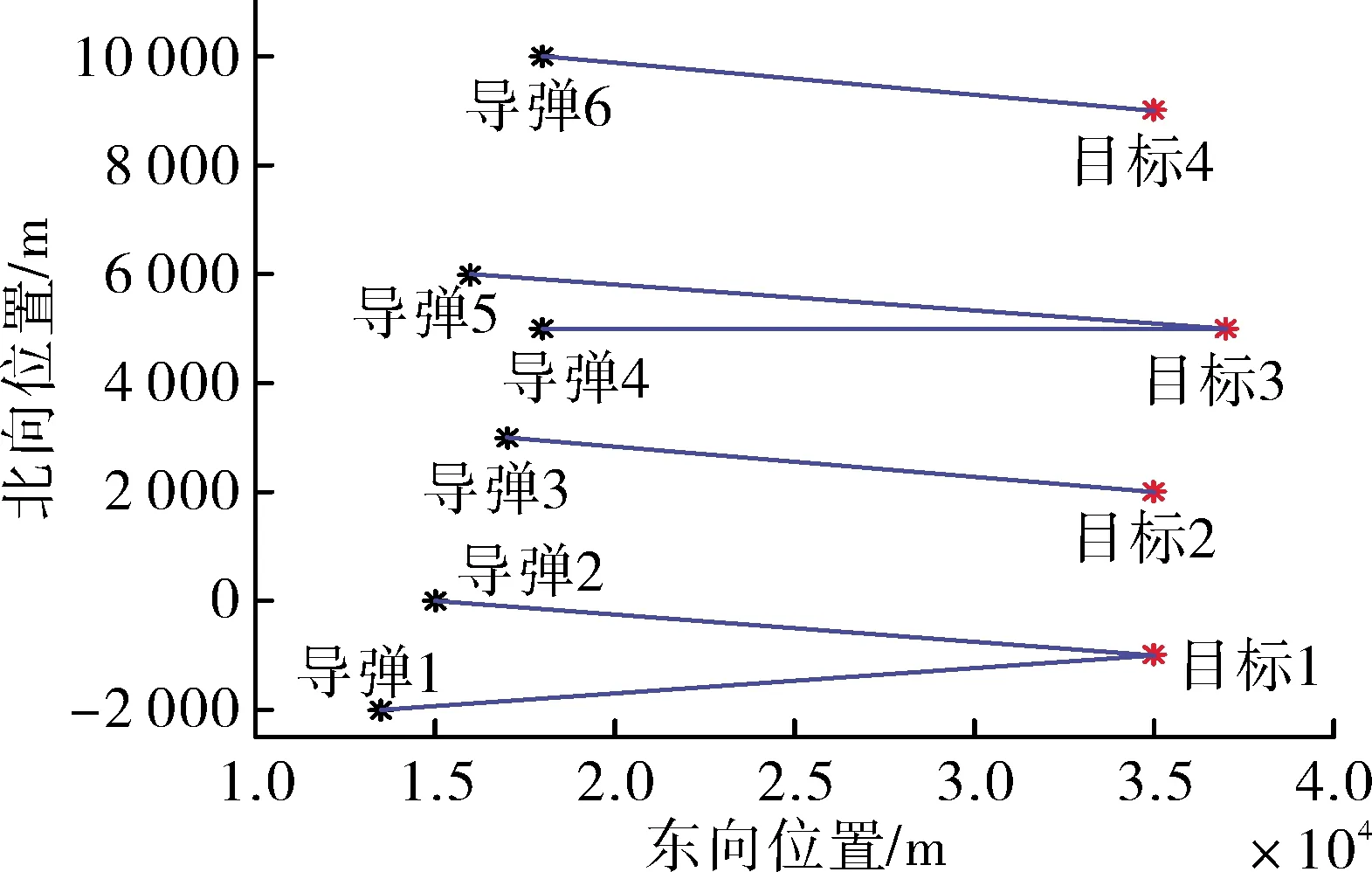
图9 目标分配结果

由仿真结果可以看出：经过5次迭代后，改进的烟花算法找到了最优的目标分配方案，找到的最优分配方案与使用穷举法计算出的最优方案相同，即导弹1、导弹2拦截目标1，导弹3拦截目标2，导弹4、导弹5拦截目标3，导弹6拦截目标4，实现了最大的优势函数，且分配结果在几何关系上适合各个导弹的拦截，并满足目标分配过程中的约束条件。找到最优方案需要的时间小于0.4 s，满足了快速目标分配的要求。仿真结果证明了文中提出方法的有效性与优越性。

4 总结

对导弹拦截情况下的目标分配问题进行了一定探索性研究，提出了一种基于改进烟花算法的目标分配方法。首先分析了交战情况下的弹-目优势关系，并建立了基于综合优势函数的目标分配数学模型。为了求解目标分配模型，将差分进化算法中的交叉变异操作引入到烟花算法中，提出了一种改进的烟花算法。在数值仿真中，首先通过标准函数的测试证明了改进烟花算法具有较好的收敛性与全局搜索能力，之后将改进的烟花算法用于求解目标分配问题，仿真结果证明使用提出的方法可以快速地找到最优分配方法，验证了算法的有效性。