一种面向效率的系统多序参量识别方法

温 馨，周佳子

(沈阳工业大学 管理学院，辽宁 沈阳 110870)

0 引言

自协同学创始人哈肯将序参量一词引入系统自组织过程研究后，序参量这一概念，在协同学应用于管理、经济、社会等领域后得到了深入的拓展。在以往关于序参量应用的研究中，国内外学者主要关注序参量识别方面的研究，例如：利用线性均衡点，通过对快、慢变量的识别，以快变量消除之后的慢变量即为序参量[1]；通过零售商和制造商之间的协同度来建立识别序参量的模型[2]；运用协同学与灰色系统建模方法构建识别序参量的系统演化模型[3];采用弛豫系数法识别序参量[4]；以目标规划模型的主旋律分析方法识别序参量[5]。在对序参量进行识别研究的同时，学者们也对序参量在协同演化过程中所起的作用进行研究，其认为序参量对系统的协同演化起到了支配和主宰的作用[6]；并对交互系统的三个维度产生系统效用[7]；在5G时代的引领下，相关学者运用熵权法对电子商务—大数据系统的序参量进行识别[8]。纵观这些研究成果，仍然没有突破哈肯模型的限制，或者对哈肯模型进行不同程度的拓展。在经典的哈肯模型中，对序参量的识别也只是停留在宏观层面上，缺少对系统演化过程中各环节的详细信息的分析，并且通过哈肯模型对系统的分析，只能识别出少量的序参量，而在系统演化实践中，特别是社会组织系统在演化变革过程中往往会产生多个序参量。基于此，针对社会组织系统演化的特殊性，本文提出一种面向效率的系统多序参量识别方法，以期为序参量的识别提供新的思路和方法。

本质上，一个开放系统由于受到内部或外部环境的干扰，系统整体会远离之前的平衡状态，并通过信息、物质及能量来与外界进行交换。系统通过与外界能量的不断转换，其利用能量效率不断提升的同时，系统演化的效率也不断提高。在系统的能量耗散过程中，可以采用投入指标和产出指标来对指标体系进行划分，在目前的研究方法中，数据包络分析作为经典的投入产出测算方法，通过建立系统投入、产出指标数据的非参数数学模型，并对决策单元在一定时期内进行评价，最终获取各决策单元间的相对有效性。运用数据包络进行评价有以下两点优势：(1)通过输入、输出变量之间的加权和来度量决策单元之间的效率，则投入、产出之间的函数关系可以不予考虑；(2)投入产出的变量权重以DEA模型计算得出，不需预估任何参数与权重，计算结果较为客观。上述优势使得数据包络方法应用于各种效率评价[9～11]和效率测度[12,13]研究。因此本文拟运用投入产出效率的理论方法，以竞优理论为研究依据，运用改进的数据包络分析方法，构建面向效率的系统多序参量识别模型。

1 面向效率的系统演化分析及序参量识别原理

根据序参量的定义，序参量可以表示系统状态，系统在演化过程中，从最初的无序状态通过序参量的作用变为有序状态，最终趋于平衡有序，序参量在系统演化中主导了系统的发展趋势。在系统变革过程中，序参量在驱动系统发展时，其可能是子系统间的协同演化，亦可能是内部子系统的整体变革，或者是系统外部因素的微小调整。若微小的涨落随着线性作用的驱动无限放大为巨涨落，巨涨落随着时间的发展到达临界点时，新形成的有序结构将替代杂乱无序的旧结构，同时耗散结构形成。系统路径在耗散结构的循环交替过程下进行演化，同时系统组织在各个演化阶段下，为达到稳定状态，子系统产生序参量，随着序参量效率的升高，系统的有序程度也随之增强。当系统达到一定有序度时，对能量的利用率也在不断提升，因此，在系统演化过程中，系统能量利用效率的表现状态，可以间接表示系统的有序程度，即系统演化过程有序度的提高也是系统对能量利用率的提高。以目前研究成果来看，以能量利用率来分析系统演化的方法难度较大，因此学者们以投入产出的角度来分析系统内部各部门之间的相互关系，并以全要素生产率为衡量的依据。

在系统演化过程中，变量对系统状态的描述可以反应在数值上，并通过数值大小的不同来映射子系统的发展状态。在评价的过程中，变量的权重系数可以表示评价的最终结果,并驱动着系统的发展。因此在实际的研究中，序参量可以表征为一组反应变量重要程度的权重系数向量。本文通过数据包络分析方法，对系统演化过程的耗散过程，通过投入指标和产出指标来划分指标体系，并以分析投入产出效率来分析系统演化过程的能量耗散效应。若将系统设定为一系列的生产过程，系统的发展过程可以理解为从初级阶段向终级阶段的变化，在变化的过程中，存在价值转移并产生价值增值的现象。在系统达到有序的状态时，其产生的价值也越大，则系统对能量的利用率也越高。因此，序参量的识别就是对每个系统个体投入指标和产出指标的价值参数的识别。

2 面向效率的系统多序参量识别方法

系统演化过程中，外界能量与系统内部要素自由交互时，系统组织开始形成能量的耗散，同时为序参量的产生提供动能。依据系统演化过程投入产出效率的特性，计算面向效率的系统个体价值参数，以改进的数据包络分析方法，建立面向效率的多序参量识别模型，进而识别系统的多序参量。

2.1 客观价值参数识别模型

(1)模型假设

实际生产中，社会组织系统要想确保生产顺利发展，其首要条件就是要素的投入，即现实生产中的“无本万利”情况很难存在，但管理者必然是希望在获得最大产出的同时投入最少的要素。成本的投入和运营费用的投入都是日常生产中系统组织运营必不可少的，因此本研究提出组织运行的公理假设：任何系统组织在实际运营中其投入要素均大于0；系统在有限时间和有限个体的约束下，这些个体在运营发展中必然拥有非负下限，转换成数学公式为：vτxj>0,vτ≥ε>0,j=1,2,…,n，其中xj(j=1,2,…,n)为投入变量，v为投入指标的价值参数向量，ε为最低投入。

(2)识别基本模型

系统中的个体通过展现其优良性来推动系统整体的发展[14]。虽然投入产出思想中产出投入比越大越好，但是系统个体在实际发展中并不是无限制的。系统整体的良性发展，以群体中个体间相互协调为基础，并且每个个体的优良表现均需遵循系统群体的整体发展规律。因此，以系统整体的产出投入比限定于规定范围内来确定系统个体的价值参数。

多目标问题推演形式可以转化为面向效率的系统个体价值参数识别问题。本研究假设n个系统构成整个系统群体，记可行域D=[(x1,y1),(x2,y2),…,(xn,yn)]的个体集合构成整个系统。系统的个体中有t种类型的投入和s种类型的产出，记为xj=(x1j,x2j,…,xtj)τ,j=1,2,…,n为系统的投入变量，其中xij(xij≥0)为系统的第i(1≤i≤t)种投入量；yj=(y1j,y2j,…,yrj)τ,j=1,2,…,n为系统的产出变量，其中yrj(yrj≥0)为系统j的第r(1≤r≤s)种产出量；v=(v1,v2,…,vt)τ为t种投入的价值参数向量，u=(u1,u2,…,us)τ为j种产出的价值参数向量。在vτxj>0,j=1,2,…,n的条件下，对于系统个体的客观价值参数模型如下：

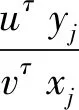
u≥0,v≥0

(1)

模型(1)的含义通俗易懂，并且表现出系统个体的不同特质。最优解不仅表示了系统个体k的活动效率，同时也解释了系统个体k如何在给定的投入产出下，获得最优的产出投入效率。

(3)客观价值参数求解方法

通过数学公式的计算，以组织行为学中“理性人”的行为假设为依据，便可对模型(1)进行求解。对数据进行标准化处理后，以 “理性人”作为假设基础(即现实生产中系统中的个体均认可 “投入是产出的前提”)，可知ε>0使得vτxj≥ε,j=1,2,…,n。

求解方法可由下列变量替换：

vτxk=t-1,tu=w,tv=λ

(2)

则模型(2)可转化为:

max(wτyk)

(3)

sub.to:wτyj-λτxj≤cj,j=1,2,…,n

(3a)

λτxk=1

(3b)

(3c)

w≥0,λ≥0

(3d)

其中，cj>0是无法确定的常数；向量λ由约束条件式(3b)λτxk=1保证不恒为0；并且w也可由模型(3)来保证不恒为0。

从形式上看模型(3)与DEA模型存在相似性，但二者本质却存在很大区别。具体表现为，第一行约束条件(3a)表示系统个体k以群体的发展规律来发展自身个体，即系统群体中的各个成员认可了个体的产出投入效率。

事实上，由于生产运营中ε的难以确定则cj也难以确定。cj在影响模型(3)结果的同时，还表示决策单元j产出投入效率的上限。在求解cj的众多方法中，系统个体往往注重最小投入和最大产出评价指标的考核，因此，本文选取以下公式：

(4)

(5)

2.2 多序参量的识别

序参量作为被系统中大多个体承认的“主流价值观”，其本身也遵从系统的发展规律。在一般情况下，由于子系统间的差异，则系统的发展目标也存在差异，则系统群体中会存在多个主流价值观的情况。在系统群体的发展中，存在多少个序参量便有多少个“主流价值观”与之对应，同样对应的每个“主流价值观”都可对系统的成员进行评价，随即也可得到系统成员在价值观下的排序情况，可排序意味着可择优[15]。在识别序参量时有以下两个步骤：其一，通过公式计算出价值参数，并对其聚类分析，进而得到系统的“主流价值观”；其二，计算系统群体在每个“主流价值观”下的顺序结构与理想状态的顺序结构的相似度，确定序参量。求解过程为：

(1)确定“主流价值观”

(2)识别多序参量

其中群体投入指标理想价值参数v*和产出指标理想价值参数u*可由公式(5)得到：

(6)

式(7)可由式(6)代入(1)的目标函数中得到：

(7)

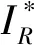
(3)多序参量的识别方法

(8)

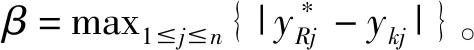
(9)

通过式子(9)可得到cRK的取值范围为[0.5,1]。因此，在系统全部“主流价值观”下，支配系统中每个个体发展的序参量即为拥有较大相似系数(cRK)的“主流价值观”。

2.3 多序参量的结果分析

(1)系统个体多序参量下结果分析

系统组织中投入产出效率的逐渐提高，是系统组织内多个序参量之间相互协作下，组织系统由无序到有序或从低级有序向高级有序的演化过程。尽管所求出的序参量得到系统“主流价值观”的认同，但其对系统个体k的引导作用却迥然有别。若系统群体中的全部个体在某一序参量下存在极高效率，则此序参量便可作为系统个体的调控序参量。作为系统群体发展变革的有效依据，整个系统给的有效发展由调控序参量的价值观引领。

(10)

(2)系统群体多序参量下调控策略

系统在发展中，若作为调控序参量的某个序参量下的个体个数远多于该系统下的其他序参量，并且该序参量在系统发展中起到主导作用，则此序参量就是系统群体在效率表征下的主流序参量。主流序参量在系统发展中对系统个体起到引导作用，并且对多个系统的群体发展评价提供明确的理论依据。

3 算例

3.1 群体中投入产出价值参数计算

本研究选取的样本数据为M行业同N企业相似的35家企业。通过对研究M行业的N企业在行业发展过程中序参量的情况，可进一步确定企业的投入产出效率的影响状况。36家企业的投入产出指标标准化数据如表1所示，其中数据编号1为N企业。

表1 36家企业投入产出标准化数据

把表1中数据代入模型(4)可求得系统个体的价值参数，表2所示。

表2 系统个体的价值参数

3.2 多序参量的识别

(1)提取“主流价值观”

以上文分析为依据，运用SPSS 19.0软件聚类分析系统群体的价值参数集合，并根据距离远近的标准确定“主流价值观”。图1为“主流价值观”的提取过程。

图1 “主流价值观”提取过程图

表3 系统群体“主流价值观”

通过计算可得理想价值参数(u*,v*)=(0.1493，0.0406， 0.715，0.0951，0.65，0.35)τ。

(2)多序参量的识别

通过公式(8)和公式(9)可求得相似系数Cn(n=1,2,3)，若Cn的值超过0.8，则此“主流价值观”就是序参量，并且改“主流价值观”对系统中的个体产生支配和引导的作用。因此，序参量的确定是通过对系统群体下“主流价值观”的排名向量与对应理想价值参数下的排名向量的相似系数来确定。表4所示为对应的相似系数。

表4 相似系数

3.3 多序参量的调控分析

系统中的个体在不同序参量下的支配结果各不相同，其本质为系统个体在不同序参量下的协作与竞争关系，同时展现出不同的效率。系统个体的调控序参量可通过计算系统个体不同序参量下的效率水平确定。表5为系统个体在不同序参量下的顺序。

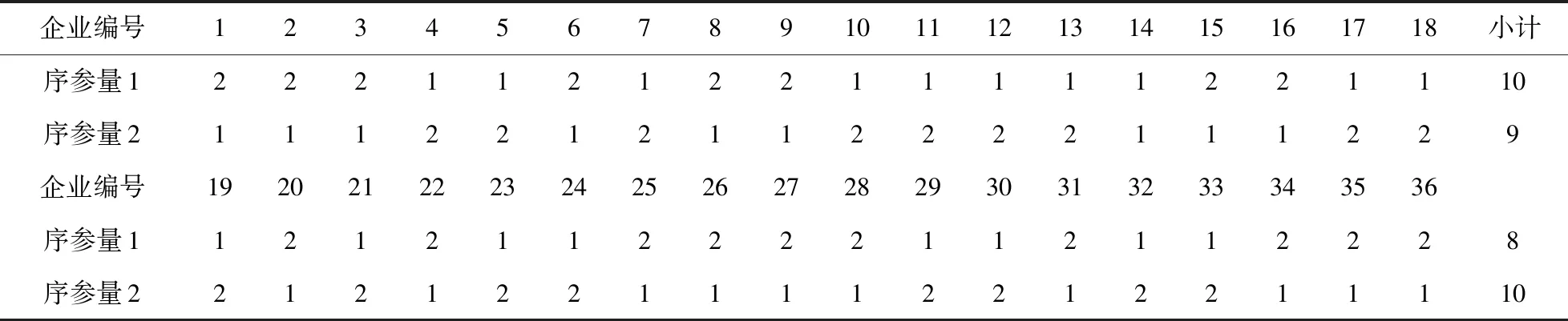
表5 系统个体在不同序参量下的顺序

(1)系统个体发展过程多序参量调控分析

(2)系统群体发展过程多序参量调控分析

从经济学角度来考虑，以识别出的序参量对组织系统进行调控，在本质上是对系统内部资源的有机配置，不管是成本、效率还是投入、产出，对各种生产要素最佳比例的运用，以实现最大的产出投入比。企业N作为一个经济系统，各部门的生产经营及服务过程共同组成了企业的演化过程，其要素产生的价值会通过一系列的生产过程转化为市场中的经济价值，而经济价值的宏观表现即为组织系统的有序化程度，有序程度的提高会带来产品价值的增大，即要素的利用率越高。以识别出的序参量对组织系统进行调控，可以提高组织的有序性，进而提升系统内各要素的利用率，增加系统组织的社会经济价值，促进系统良性发展。

4 结论

对系统组织演化过程中产生多序参量的识别，是目前系统组织如何有效的应对外部多变环境的关键问题。文章应用系统演化过程中能量的耗散特性，研究了序参量的产生机理，提出了面向效率的多序参量识别方法。本研究的主要创新性和应用价值体现在：1)理论研究方面，本文基于协同学原理，通过耗散结构思想，应用投入产出视角，分析了面向效率的系统多序参量作用机理，丰富了系统演化过程中序参量的内涵；2)研究方法方面，通过提出面向效率的多序参量识别方法，弥补了以往研究方法的不足，为系统演化效率下多序参量的识别提供了有效的方法；3)技术应用方面，该方法识别出的序参量，可以进一步演化为系统发展过程中的投入产出效率，为有序性的调控问题提供技术支持。