考虑蠕虫传播风险的信任度更新模型
2020-11-10李艳博宋明秋
李艳博,宋明秋
(大连理工大学 经济管理学院,辽宁 大连 116024)
0 引言
蠕虫是一种广泛流传的恶意代码类型,它具有自我复制和主动传播的特性。一旦网络中的主机被蠕虫感染,蠕虫将会借助被感染主机发起对其他主机的新攻击,从而造成大规模的主机瘫痪,给整个网络带来不可估量的损失。随着信息技术的快速发展,蠕虫不断进化出新的攻击形式,例如近年在全球蔓延的蠕虫式勒索软件,其危害和杀伤力都是巨大的,因此对于蠕虫防御的研究一直都是网络安全领域的重要问题之一。传统的蠕虫防御方法主要是入侵检测,它通过安全策略、特征检测等方式来发现和判别网络中的入侵行为[1,2]。当检测到特定的入侵后,会自动触发阻止攻击的操作,并通过改变环境等方法来修复导致入侵发生的漏洞。入侵检测是一种基于行为的被动检测,由于检测异常行为需要与特征库中的已知攻击行为进行对比,因此它对已知攻击的检测准确性高,而对未知攻击的检测准确性低。近年来,基于信任模型的管理机制被广泛应用到蠕虫攻击的防御,它是一种主动管理的防御网络蠕虫攻击的方法[3,4],通过评估节点的信任度能有效识别网络中的恶意节点,并根据节点信任度构建可信交互路径来规避恶意攻击,从而提高节点的机密性和完整性[5,6]。因此网络节点信任度的度量成为信任机制能否有效规避恶意攻击的关键问题。
在已有信任模型研究中,出现了基于模糊逻辑推理的声望模型[7]、集中式的信任模型[8]以及基于推荐的信任模型[9,10]等,其中基于推荐的信任模型应用最为广泛。它结合了节点间的直接交易历史以及第三方推荐节点提供的交易信息两方面内容,使得对节点的信任度评估更加全面和准确。Eigen Trust模型[9]是一种基于推荐的全局信任机制,在计算信任度时考虑了所有交易历史。但是该模型将推荐节点的可信度用节点的直接信任度代替,而实际网络中节点提供推荐信息的可信度并不等同于节点交易的信任度,因而使模型的准确性大大降低。姜守旭等[11]在信任模型中明确了节点交易行为可信度和推荐节点评价可信度的差异性,并根据源节点和推荐节点对目标节点信任度评价的一致性给出了推荐节点可信度评价的计算方法。文献[12]在基于攻击传播性的信任模型中对推荐节点的可信度进行了定义和说明,并根据攻击传播性的特点给出了推荐可信度的更新计算方法。
以上基于推荐的信任模型都是根据节点间的交易行为建立的,通过统计节点间交易结果的正确与否次数来计算信任度,此类计算方法不能使信任度对恶意攻击行为做出快速反应。为了解决这个问题,对恶意节点的惩罚机制被引入到信任模型。马满福等[13]认为与恶意节点有联系的所有节点的信任度都应该受到缩减,并将此机制称为连带惩罚。叶正旺等[14]建立了一个和交易次数相关的惩罚函数和调节函数,分别实现了短时间内不成功交易次数剧增时信任值的快速下降以及短时间内成功交易次数剧增时信任值的缓慢提升。在电子商务以及企业信任模型的研究中,汪克文[8]和徐彪[15]引入了一种新的惩罚机制,该机制在考虑交易次数的同时,还分别关注了失败金额和负面事件的严重程度,这两个因素都直接反映了交易事件对节点造成的影响。
此外,网络节点间交易失败带来的影响也可以用恶意攻击行为产生的安全风险来表示,因此风险作为对信任的一种补充被加入到信任模型[16]。田春岐等[17]提出了一种基于信誉和风险的信任模型,该模型用信息熵量化了恶意节点攻击带来的不确定性风险值,并将风险作为对信誉度的补充添加到信任模型中。仿真结果表明该模型能够有效识别恶意节点,较大程度提高了系统成功交易率。但是该模型在计算风险值时仅根据直接交易结果考虑了节点的潜在威胁,忽略了推荐节点提供的信息中隐含的风险因素。
综上,现有信任模型忽略了蠕虫传播过程中隐含的风险因素,从而造成对信任度的刻画不够准确。针对这一问题,本文建立了考虑蠕虫传播风险的信任度更新模型。首先对蠕虫的传播过程进行了详细分析,发现信任度是影响蠕虫传播的关键因素,由此定量化描述了信任度和传播概率的关系并构建了蠕虫传播模型。然后结合蠕虫的传播过程,在基本信任模型的基础上,讨论了信任度对蠕虫传播风险的响应作用,分别在直接风险、间接风险和传播性风险三种条件下对信任度进行了更新计算:(1)引入直接风险系数描述节点直接信任度和推荐可信度对直接风险的响应关系;(2)引入间接风险系数描述节点信任度对间接风险的响应关系;(3)引入传播性风险系数描述节点信任度对传播性风险的响应关系。最后以无标度网络作为基础网络模型,仿真分析了信任度对蠕虫传播演化趋势的影响,验证了考虑蠕虫传播风险的信任度更新模型的有效性。本文模型可用于实际网络中信息传输可信路径的构建,通过节点间的历史交互行为以及节点对风险的感知来动态计算节点信任度,进而判别节点的可信级别,避免将安全级别要求高的数据包传输给可信级别低、具有潜在威胁的网络恶意节点,保证信息传输的安全性。
1 蠕虫传播模型
1.1 蠕虫传播过程分析
蠕虫是一种智能化的、不需要人工干预就可独立运行的攻击程序。该程序包含四个功能模块,分别是信息搜集、扫描探测、攻击渗透和自我复制[18]。其中,攻击渗透是主体模块,包含发起攻击和入侵渗透两个过程,本文将这两个过程分别定义为蠕虫的传播过程和感染过程。
(1)蠕虫的传播过程:蠕虫借助感染状态节点向邻居节点发起攻击,主要行为包括建立节点间的信息传输通道以及借助此通道将蠕虫副本传送给邻居节点。传播过程可看作是感染状态节点和邻居节点的一次信息交易过程。由于信息交易的成功与否取决于节点间的信任关系[19],该值可以用概率形式的信任度来刻画,因此邻居节点对感染状态节点的信任度会影响两节点间的信息交易过程,从而影响蠕虫的传播过程。信任度越大,信息交易越容易成功,蠕虫传播成功的概率越大。基于以上分析,本文在建立蠕虫传播模型时引入了信任度指标。
(2)蠕虫的感染过程:当副本文件成功传送到节点后,蠕虫开始入侵渗透,不断对节点造成破坏,增加其脆弱性,直至攻破该节点。节点被感染的概率和该节点的脆弱性相关。节点越脆弱,其被感染的概率越大。
1.2 节点状态描述
根据上述分析,本文建立了蠕虫传播模型STIDR,节点状态的具体描述如下:
S:表示易感状态(Susceptible),S状态节点存在漏洞,可能会受到蠕虫攻击;
T:表示威胁状态(Threatened),T状态节点已经受到蠕虫攻击,还没有被感染,不具备传播和感染能力;
I:表示感染状态(Infectious),I状态节点已经被蠕虫成功感染,具备传播和感染能力;
D:表示隔离状态(Detached),它是节点的一种附加状态;
R:表示免疫状态(Recovered),R状态节点已获得免疫能力,不会被蠕虫感染,也不具备感染其他节点的能力。

1.3 蠕虫传播建模
在STIDR模型中,节点的状态转换关系如图1所示。其中各参数定义为:α表示传播概率,描述节点由易感状态S转变为威胁状态T的概率;β表示感染概率,描述了节点由威胁状态T转变为感染状态I的概率;δ1表示易感状态节点的免疫概率,描述节点由易感状态S转变为免疫状态R的概率;δ2表示感染状态节点的免疫概率,描述节点由感染状态I转变为免疫状态R的概率。
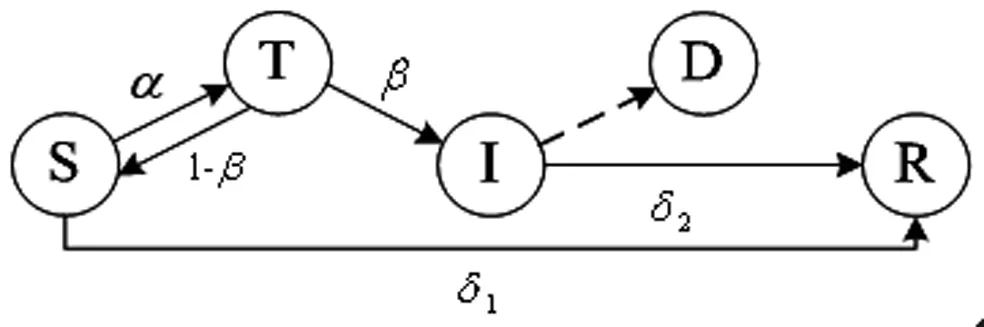
图1 STIDR模型的状态转换图
根据图1中节点的状态转换关系,本文分析了网络中节点的状态转换规则,并参照文献[20]中的状态转移概率法建立了蠕虫传播动力学方程,具体如下:
(1)当节点i处于易感状态S时,它存在的状态转换关系有S→T和S→R,若未发生以上两种状态转换,则保持原状态S。
a.节点i以概率δ1转变为免疫状态R。
b.当节点i受到邻居感染状态节点j的攻击时,它会以概率αij转变为威胁状态T,或以概率1-αij保持原状态S。当节点i存在多个邻居感染状态节点时,它成功受到至少一个邻居感染状态节点jk的攻击就会发生S→T的状态转变,否则保持原状态,由此可知节点i和这些邻居感染状态节点的交互过程对于S→T转变是"或关系",对于保持原状态S是"与关系",这些交互过程中使节点i发生S→T转变的数目是当前时刻该节点受到的攻击数目KIS。
根据上面的分析,易感状态节点i的状态转换动力学方程见式(1)。
(1)
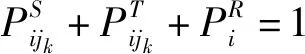
(2)
Si(t+1)=MultiRealize[Pi(t+1)]
(3)

αij=μOTij
(4)
(2)当节点i处于威胁状态T时,它存在的状态转换关系有T→I和T→S。T→I的转变对应蠕虫的感染过程,β表示节点的感染概率,则节点i以概率β转变为感染状态I,或以概率1-β转变为易感状态S。考虑攻击相关性,节点的感染概率和当前时刻受到的攻击数目KIS相关,计算公式为β=β0+β1×KIS,其中β0表示感染概率初始值,β1表示感染概率变化率。威胁状态节点i的状态转换动力学方程见式(5)。
(5)
(6)
Si(t+1)=MultiRealize[Pi(t+1)]
(7)
(3)当节点i处于感染状态I时,它会以概率δ2转变为免疫状态R或以概率1-δ2保持原状态I。则感染状态节点i的状态转换动力学方程见式(8)。
(8)
(9)
Si(t+1)=MultiRealize[Pi(t+1)]
(10)
(4)当节点i识别邻居节点j是感染状态节点后,会主动采取安全策略来断开与该节点的连接。此时,对于节点i来说,节点j由感染状态I转变为隔离状态D。隔离状态是节点i对节点j所处状态的主观判断,是节点i赋给节点j的一种附加状态,并不会影响节点j真实状态的转变过程。因此,本文不再对隔离状态的转变进行具体说明。
2 考虑蠕虫传播风险的信任度更新模型
2.1 基本信任模型
信任模型大多都是根据节点间的交易行为建立的。通过对历史交易记录的分析,推算对节点未来交易行为的期望值。节点的交易行为是指服务请求节点向服务提供节点发起请求,服务提供节点响应请求并向服务请求节点传送相应的服务文件[21]。现有大多信任模型都是站在服务请求节点的角度计算服务提供节点的信任度。而实际网络中节点具有双重身份,既可以作为服务请求者也可以作为服务提供者[22]。因此,本文在计算节点信任度时不再区分服务提供者和服务请求者的身份,而是将交易行为看作是信息传递的过程,将发生交易行为的两方分别定义为信息发送方和信息接收方,如图2所示。在发生交易行为时,信息接收方i通过信任度评估来判别信息发送方j的身份。在这个过程中,信息接收方i是信任度评估中的源节点,信息发送方j是目标节点,节点i和节点j的共有邻居节点m是推荐节点。
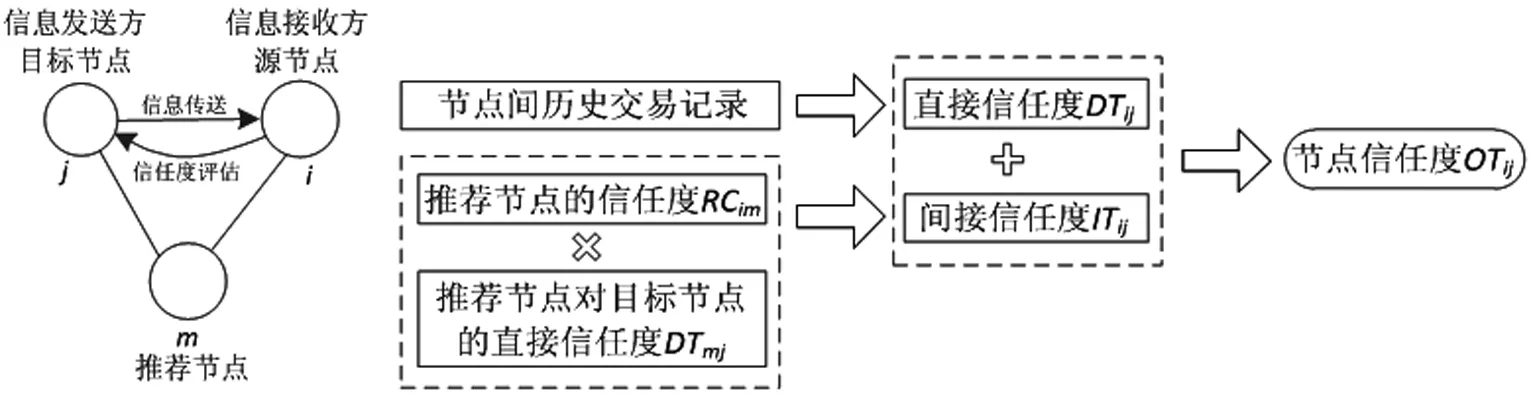
图2 信任模型的节点示意图 图3 信任模型
图3展示了信任模型中的参数构成以及各参数之间的关系。本文参照文献[4,12,23]对节点信任度、直接信任度、间接信任度以及推荐可信度的相关概念、符号表示以及计算过程进行了具体说明。
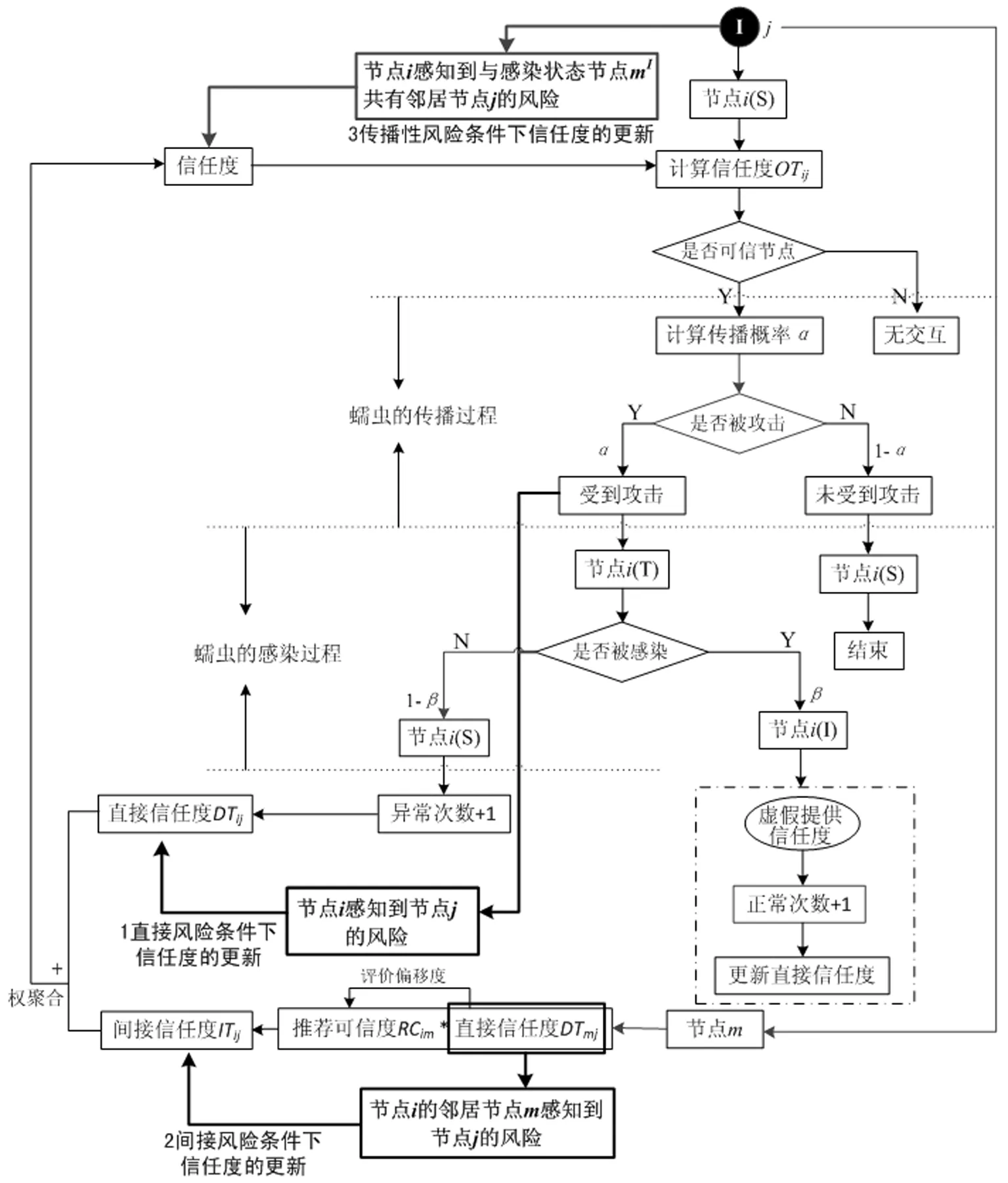
节点信任度是源节点对目标节点未来行为的期望值,用OT表示。节点信任度由直接信任度DT和间接信任度IT加权构成,计算公式见式(11)。其中,θ是加权因子。本文设置了信任度阈值T*,当OTij OTij=θ·DTij+(1-θ)·ITij (11) 直接信任度是源节点根据与目标节点的直接交易历史对目标节点未来行为的期望值,用DT表示。参考文献[24],节点i和节点j的直接信任度服从Beta分布,以交易正常次数占总次数的比作为信任度,计算公式见式(12)。Sij和Fij分别代表节点j与节点i交易正常和交易异常的次数。节点间交易正常的次数越多,节点间的信任度越高。 (12) 在计算当前时刻的直接信任度时需要综合考虑历史信任度信息。本文引入了时间衰减函数f(k),表示第k个时间区间内发生的交易相比当前时间区间内交易的折扣幅度函数,具体计算过程见式(13),ρ为时间衰减因子。考虑了时间衰减函数后,直接信任度的计算公式变为式(14): f(k)=fk=ρn-k (13) (14) 间接信任度是源节点根据推荐节点提供的信任度对目标节点未来行为的期望值,用IT表示。本文将推荐节点提供的信任度称为推荐信任度。推荐信任度是推荐节点对目标节点的直接信任度。间接信任度由推荐可信度加权构成,计算公式见式(15)。其中,推荐可信度RC是一个加权系数,M是推荐节点m的集合。推荐节点是两节点的共有邻居节点,为了消除感染状态节点提供虚假信任度的影响,本文去除了推荐节点中对源节点不可信的节点。 (15) 推荐可信度描述了推荐节点提供推荐信任度的可信任程度,用RC表示。推荐节点中可能存在正常节点(S节点、R节点)或恶意节点(I节点),其中正常节点提供客观的信任度,而恶意节点提供虚假的信任度。因此,在对推荐可信度进行更新时需要提高正常节点的推荐可信度并降低异常节点的推荐可信度。文献[12]设置了推荐节点可信度评估机制:首先根据所有邻居节点的推荐信任度来计算评价偏移度ε,ε的大小表示了节点的可信程度,然后根据ε对推荐节点进行奖惩,具体计算方法如下: (16) (17) 2.2.1 考虑蠕虫传播风险的信任度更新过程 本文结合蠕虫的传播过程和感染过程,针对不同状态节点受到攻击的反应来分析信任度的更新过程。网络中节点的状态有S、T、I、D、R五种,其中D是节点的一种附加状态,不会影响节点真实状态的信任度更新。T是S到I的一种中间状态。节点经历蠕虫的传播过程由状态S变为状态T后,会再经历蠕虫的感染过程。若节点被感染则变为状态I,否则返回状态S,由此发现节点不会在状态T停留。因此,本文在信任度更新部分不再对D、T节点进行分析。下面将具体讨论S、I、R状态节点在蠕虫传播网络中信任度的更新过程,图4是蠕虫传播过程中信任度的更新框架。 图4 信任度的更新框架 (1)当易感状态节点i受到邻居感染状态节点j发起的蠕虫攻击时,它会经历蠕虫的传播过程和感染过程。节点i对节点j的信任度会根据这两个过程的结果进行动态更新。本文分三种情况讨论了信任度的更新过程: 第一种情况:图4中,当节点i以概率α受到感染状态节点j的攻击,以概率1-β未被感染时,节点交易记作异常,交易异常次数Fij增加1。此时,节点i虽然没有被感染,但是已经感知到节点j的风险,本文将此部分风险定义为直接风险。在对节点j进行信任度评估时需要对直接风险进行响应,具体计算见2.2.2节。 定义1直接风险 源节点通过直接交易过程感知的目标节点的风险是直接风险。 第二种情况:图4中,当邻居节点m感知到节点j的直接风险后,它会通过推荐信任度传给节点i。此时,节点i也间接地感知到节点j的风险,本文将此部分风险定义为间接风险。间接风险也会影响目标节点j的信任度,具体计算见2.2.3节。 定义2间接风险 源节点从推荐信任度中感知的推荐节点对目标节点的直接风险是间接风险。 第三种情况:图4中,节点i和节点j存在共有邻居节点mI。当节点i认定节点mI为感染状态节点时(OTimI) 定义3传播性风险 源节点通过传播性作用感知的目标节点的潜在风险是传播性风险。 图5 传播性风险示意图 (2)蠕虫攻击计算机的实质是在利益机制驱动下,从不同的角度或为达到不同目的而投入成本来促使蠕虫传播[26],因此感染状态节点为了推动蠕虫在网络中的传播会虚假提供信任度,如图4中恶意行为部分。假设在每一个时间点,感染状态节点会通过增加与邻居节点的成功交易次数来提高直接信任度,如公式(18)所示,其中Sij表示节点i与节点j的成功交易次数。 Sij=Sij+1 (18) (3)R节点具有免疫能力,可能会受到蠕虫攻击,但不会被蠕虫感染。R节点的信任度更新过程和S节点信任度更新过程保持一致。 下面将具体讨论在直接风险、间接风险和传播性风险条件下信任度的更新计算。 2.2.2 直接风险条件下信任度的更新计算 在直接风险条件下,节点i对节点j的直接信任度和推荐可信度都会受到影响,计算见式(19)和式(20)。其中,参数d和r表示直接风险系数,反映了直接信任度和推荐可信度对风险的敏感程度(d<1,r<1)。直接风险系数和节点承担的风险大小相关,由于节点当前时刻受到的攻击数目KIS能侧面反映一个节点面临的风险大小,因此本文设定dij=rij=e-KISi。则: DTij=DTij*dij (19) RCij=RCij*rij (20) 2.2.3 间接风险条件下信任度的更新计算 节点信任度对间接风险也具有响应作用。心理学研究表明,共情是一种情绪反映,是一种能够体验他人情绪状态,并受他人情绪影响的能力[27]。本文借用心理学中的"共情"概念讨论了源节点对推荐节点提供的推荐信任度中间接风险的感知以及目标节点信任度对间接风险的响应,具体表现为:在间接风险下,源节点会降低对目标节点的信任度OTij,计算公式如(21)。其中,s表示间接风险系数,反映了目标节点信任度受间接风险的影响程度。间接风险系数s和推荐节点集合M中感知到目标节点风险的节点个数kM相关,计算公式如(22)。推荐节点中感知到目标节点风险的数目越多,间接风险系数越小,信任度对间接风险的响应越强烈,目标节点的信任度下降越快。 OTij=OTij*s (21) s=e-kM (22) 2.2.4 传播性风险条件下信任度的更新计算 OTij=OTij*cij (23) (24) 研究表明,Internet网络符合无标度网络特性。因此,本文依托无标度网络进行蠕虫传播模型的仿真实验。实验目的是研究信任度对蠕虫传播的影响以及考虑蠕虫传播风险信任度更新模型的有效性。在验证模型的有效性部分,实验对比分析了直接风险、间接风险、传播性风险三种条件下,信任度更新模型和基本信任模型中信任度指标的变化及其对蠕虫传播影响的差异性。 仿真实验是依托Python实验平台,构建的无标度网络中节点总数N=1000,节点平均度 表1 实验参数设置 为了研究信任度对蠕虫传播过程的影响,本文对不考虑信任度指标、基于基本信任模型以及考虑蠕虫传播风险的信任度更新模型三种情况下的蠕虫传播过程进行了对比分析,仿真结果如图6所示。 图6 信任度对蠕虫传播过程的影响 图6分别显示了网络中S、T、I、R状态节点的数目变化情况。从图6可以看出,与不考虑信任度指标的情况相比,基本信任模型以及考虑蠕虫传播风险的信任度更新模型两种情况中S状态节点数目下降更慢,T和I状态节点数目增加更慢且峰值更低,R状态节点数目增加更慢。以上结果表明,在蠕虫传播模型中引入信任度指标在一定程度上降低了蠕虫在网络中的传播速度和传播规模,达到了抵御蠕虫攻击的目的。另外,从图6中还发现,考虑蠕虫传播风险的信任度更新模型比基本信任模型中I曲线的上升速度慢且峰值低,这表明考虑蠕虫传播风险的信任度更新有助于识别网络中的感染状态节点进而提高抵御蠕虫攻击的能力。 本文对基本信任模型以及考虑蠕虫传播风险的信任度更新模型两种情况下,信任度变化以及信任度对蠕虫传播过程的影响进行了对比分析,仿真结果如图7所示。 图7 信任度的变化及对蠕虫传播过程的影响 图7(a)展示了蠕虫传播过程中各状态节点的信任度变化过程。从图7(a)可以看出,与基本信任模型相比,考虑蠕虫传播风险的信任度更新模型中易感状态节点和免疫状态节点的信任度上升更慢,感染状态节点的信任度下降更快,符合信任值"快下降,慢增长"的目标[13]。观察图7(a)中感染状态节点I曲线,它呈现先上升后下降的趋势。信任度的上升主要是由蠕虫传播初始阶段网络中感染状态节点间相互提供虚假信任度导致的。当蠕虫传播一段时间后,网络中感染状态节点开始逐渐减少,提供虚假信任度的节点占比减少,同时易感状态和免疫状态节点通过直接交易过程感知到感染状态节点的风险,对其信任度大幅降低,因此感染状态节点的信任度开始下降。以上结果表明考虑蠕虫传播风险的信任度更新能更好地识别网络中的感染状态节点。 图7(b)和(c)分别展示了蠕虫传播过程中感染状态节点和隔离状态节点的数目变化过程。图7(b)中考虑蠕虫传播风险的信任度更新模型中I曲线的峰值低于基本信任模型,图7(c)中基本信任模型的D状态节点数目变化不大,而考虑蠕虫传播风险的信任度更新模型中D曲线随着时间变化出现了明显凸起。图7(b)和(c)中的结果都表明本文考虑蠕虫传播风险的信任度更新对网络中感染状态节点的识别更加有效,被识别为感染状态的节点转变为了隔离状态,从而使蠕虫的传播受限,导致I曲线上升更慢,峰值更低。 为了研究直接风险条件下信任度更新的有效性,本文对比了基于基本信任模型以及直接风险条件下信任度更新的蠕虫传播过程,仿真结果如图8所示。 图8 信任度的变化及对蠕虫传播过程的影响 从图8(a)可以看出,直接风险条件下信任度的更新对S节点的信任度基本无影响,使I节点的信任度下降变快,R节点的信任度增加变缓,这说明直接风险条件下的信任度更新可以帮助更好地识别感染状态节点。图8(b)展示了蠕虫传播过程中I状态节点的数目变化过程。在蠕虫传播的初始阶段,基本信任模型和直接风险条件下信任度更新中I曲线的增长速度基本保持一致,这是因为此阶段网络中的I状态节点数目还比较少,信任度对直接风险的响应还不敏感。随着t的增加,直接风险系数的影响作用开始显现,两种情况中I状态节点数目逐渐出现差异。相比于基本信任模型,直接风险条件下信任度更新中I曲线峰值更低。观察图8(c)中的D曲线,直接风险条件下信任度更新中的D曲线随着时间变化出现了凸起,峰值达到300,而基本信任模型中的D曲线变化不大。图8(b)中I曲线和(c)中D曲线的差异性都表明通过对直接信任度和推荐可信度的惩罚达到了识别感染状态节点以及抵御蠕虫攻击的目的。 为了研究间接风险条件下信任度更新的有效性,本文对比了基于基本模型以及间接风险条件下信任度更新的蠕虫传播过程,仿真结果如图9所示。 从图9(a)可以看出,间接风险条件下信任度的更新对S状态节点的信任度基本无影响,使I和R状态节点的信任度始终低于基本信任模型中的信任度。观察图9(b),当t在0~2时,两种情况下的I状态节点数目差别不大,这是因为刚开始时节点间的信任度为初始化直接信任度0.5,节点间的信任度比较低,节点间信息交易成功的概率比较小,感知到蠕虫传播风险的节点数目少,从而使间接风险条件下的信任度更新对蠕虫传播的影响很小。随着t的增大,网络中I状态节点数目增多,感知到风险的节点通过推荐信任度帮助源节点识别感染状态节点,信任度更新的作用开始显现,I状态节点的数目表现出差异性。图9(c)中间接风险条件下信任度更新的D曲线相比于基本信任模型的D曲线出现了明显凸起。以上实验结果都表明,间接风险条件下的信任度更新在一定程度上能更好地识别感染状态节点以及抑制蠕虫在网络中的传播。 图9 信任度的变化及对蠕虫传播过程的影响 图10 信任度的变化及对蠕虫传播过程的影响 为了研究传播性风险下信任度更新的有效性,本文对比了基于基本模型以及传播性风险条件下信任度更新的蠕虫传播过程,仿真结果如图10所示。 从图10(a)可以看出,传播性风险条件下信任度的更新使S、I和R状态节点的信任度都低于基本信任模型中对应状态节点的信任度。观察图10(b),在I曲线的上升阶段,传播性风险条件下信任度更新中I状态节点数目始终低于基本信任模型中I状态节点数目,验证了传播性风险条件下信任度更新的有效性。考虑传播性风险后,S和R状态节点会认为与I状态节点相连接的正常节点(S或R状态)在下一时刻存在转变为I状态的可能性,因此会降低这部分节点的信任度。如果与I状态节点相连接的节点在下一时刻没有变为I状态,那么会导致对这些正常节点的信任度偏低,这与图10(a)中传播性风险条件下信任度更新中S和R状态节点的信任度低于基本信任模型相符。在图10(c)中,传播性风险条件下信任度更新中D状态节点数目要多于基本信任模型中D状态节点数目。总体来说,信任度对传播性风险的响应在一定程度上有助于识别感染状态节点,进而抵御蠕虫攻击。 本文首先建立了蠕虫传播模型,讨论了信任度指标对蠕虫传播的影响作用,并对信任度和传播概率的关系进行了定量描述。然后针对现有信任模型中信任度计算不准确的问题,提出了考虑蠕虫传播风险的信任度更新模型,分别在直接风险、间接风险以及传播性风险三种条件下对信任度进行了更新计算,最后依托无标度网络进行了仿真实验。结果表明,在蠕虫传播模型中引入信任度指标可以降低蠕虫在网络中的传播速度和传播规模,达到了抵御蠕虫攻击的目的;相比于基本信任模型,考虑蠕虫传播风险的信任度更新模型使感染状态节点的信任度下降更快,易感状态节点和免疫状态节点的信任度提升更慢,符合信任值"快下降,慢增长"的目标。直接风险、间接风险和传播性风险三种条件下的信任度更新都在不同程度上降低了感染状态节点的信任度以及蠕虫在网络中的传播速度,其中直接风险的作用最为明显。 本文考虑蠕虫传播风险的信任度更新模型丰富了网络信任相关领域的研究,为信任度的准确刻画提供了一种新方法。在实际应用中,本文模型可用于评估可信网络中节点的安全性。通过引入风险系数,根据节点间交易结果的变化来动态更新节点的信任度,帮助节点更有效地识别潜在威胁,防御和对抗蠕虫攻击。本文模型涉及了节点对蠕虫传播风险的感知,对于有些隐蔽性强的攻击,主机并不能有效地感知恶意节点的威胁,这将会影响信任度对风险的响应,因此,如何提升主机对恶意行为的识别能力和检测能力是作者后续研究的重点。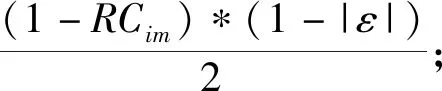
2.2 考虑蠕虫传播风险的信任度更新模型


3 仿真分析
3.1 实验环境

3.2 信任度对蠕虫传播过程的影响

3.3 信任度比较分析及对蠕虫传播过程的影响

3.4 直接风险条件下信任度更新及对蠕虫传播过程的影响

3.5 间接风险条件下信任度更新及对蠕虫传播过程的影响


3.6 传播性风险条件下信任度更新及对蠕虫传播过程的影响
4 结论
