椭圆管道与连接器过盈装配应力有限元分析
2020-11-10李森
李 森
(中石化胜利石油工程有限公司钻井工艺研究院, 东营 257000; 中国石油大学(华东)机电工程学院, 青岛 266580)
海底管道是海洋油气资源开发的重要基础设施之一,其安全对海上油气田的正常运行至关重要,受运营期间复杂工作载荷、环境载荷的作用,具有极大的失效概率。海底管道一旦发生失效,就会造成巨大经济损失[1],因此通过机械连接器在对其进行修复是目前应用最为广泛的方法,但由于过盈量与椭圆度因素导致过盈修复过程中出现承压失稳,影响整个管道修复的效果[2]。
中外专家与学者主要通过理论法和数值模拟法对装配过程中过盈量与椭圆度因素产生的接触应力进行研究。
关于过盈装配引起的应力分布问题,文献[3]分析了均匀内外压作用下厚壁圆筒应力、变形,推导了组合厚壁圆筒过盈配合经典解。在组合厚壁圆筒理论基础上,学者们进一步提出了多层厚壁圆筒过盈配合解、组合厚壁圆筒弹塑性统一解等理论[4-5]。王挺等[6]通过数值模拟的方法对轮轴间等效应力的大小与过盈量的关系进行研究。刘奔等[7]对油管接头螺纹及密封有限元模型进行合理简化,通过数值模拟的方法分析了过盈量对接触应力及密封性能的影响。然而,若叠加考虑管道椭圆度的影响,目前尚未有成熟的理论可直接借鉴。
关于椭圆度引起的应力分布问题,李伟健等[8]、王常文等[9]主要集中在连续油管弯曲引起椭圆度及椭圆管道承压稳定性的问题,形成了一些关于失稳临界压力的理论或经验公式。调研发现管件模压式缩颈矫圆问题与本文问题比较相似,文献[10-11]采用理论和试验方法研究了大型管件的模压位移对矫圆后的管道椭圆度的影响,遗憾的是文章未给出矫圆过程中管道应力与椭圆度的理论关系,但是,文中管端问题简化为短管问题、模压过程逆向等效等做法可借鉴至本文的研究。
综上所述,过盈量与椭圆度两种因素共同影响下管道与连接器过盈装配的问题未深入研讨,现有理论公式很难直接应用于工程。本文基于理论和数值模拟相结合的方法,简化管道-连接器过盈装配有限元模型,定义椭圆度应力系数衡量椭圆度的应力集中效应,借助数值模拟结果观察装配过程中接触应力与等效过盈量、椭圆度的关系,分析两种因素对管道承压强度的影响,基于此提出提高管道承压能力的方法。
1 厚壁圆筒基本解
针对直径误差引起的海底管道与连接器的过盈安装问题,可以借鉴组合厚壁圆筒理论进行分析。由两层圆筒过盈装配形成组合厚壁圆筒,即依靠等效过盈量δ,配合后使零件表面间产生弹性压力,从而获得紧固的连接。如图1所示,其内筒内半径为a,外筒外半径为c,配合后接触面的半径为b,外筒内半径比内筒外半径为小,两者的差值δ为套装等效过盈量,配合之后,两接触面上将产生互相挤压的装配压力p,形成紧固的静配合。在装配压力p作用下,内筒外半径会缩短δi,外筒内半径伸长δo,二者之和为等效过盈量,其中内、外筒的弹性模量、泊松比分别为Ei、Eo、μi、μo。根据厚壁圆筒基本解可知内筒和外筒接触面上位移为
(1)
由|δi|+|δo|=δ可整理出组合圆筒装配压力为
(2)
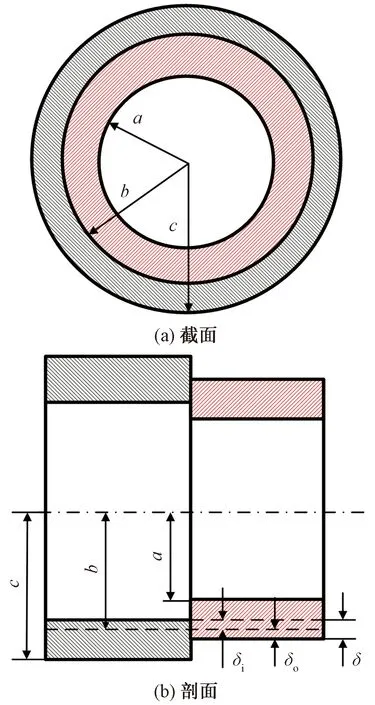
图1 组合厚壁圆筒几何模型Fig.1 The geometric model of combined thick wall cylinder
2 有限元模型及验证
2.1 管道-连接器修复连接有限元模型
通常,连接器设计时会在连接端头设置一小段坡口,以便于管道的安装,之后是过盈配合段,如图2(a)所示,其中B为等径段长度,且满足B=2L。事实上,安装过程可视为准静态过程,选取安装后的稳定状态进行建模,其中,将存在椭圆度的海底管道简化为椭圆管道,无椭圆度管道简化为标准圆管,连接器简化为标准圆筒,考虑结构对称性简化建立1/4管道-连接器修复过盈连接三维有限元模型[12],如图2(b)所示。椭圆管道如图3所示。其中管道椭圆度定义为
(3)
椭圆管道等效直径:
(4)
等效过盈量I:
(5)
式中:o为椭圆度;Dmax为椭圆管道长半轴,mm;Dmin为椭圆管道短半轴,mm;d为连接器内径,mm。
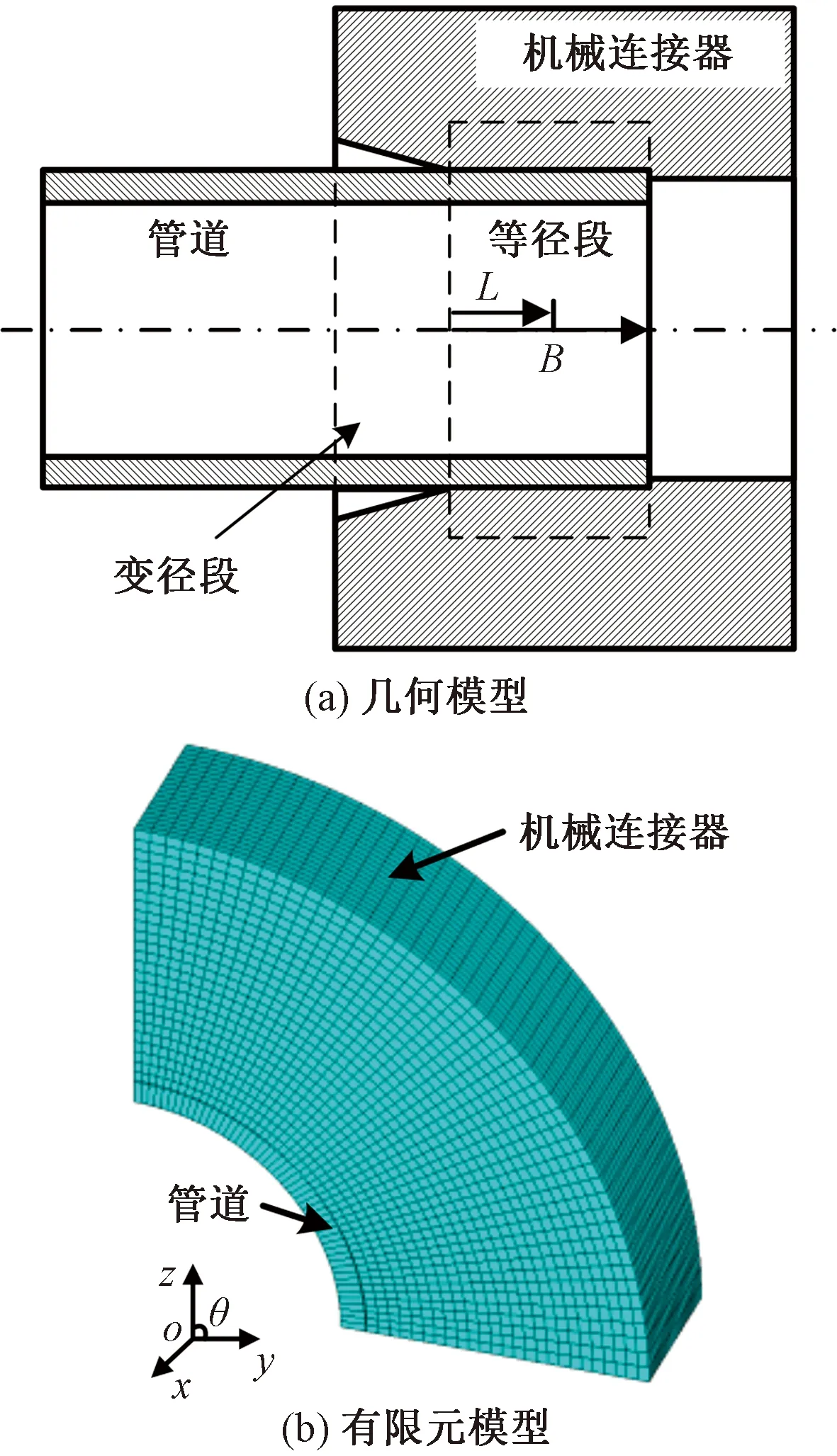
图2 海底管道与机械连接器过盈装配模型Fig.2 The interference fit model of subsea pipeline and mechanical connector

图3 椭圆管道几何模型Fig.3 The geometric model of oval pipeline
2.2 模型有效性验证
建立圆管有限元模型与组合厚壁圆筒经典理论模型,通过两者结果对比分析,验证海底管道与连接器过盈连接模型是否有效。选用单元及基本参数如表1所示。
对称面施加对称约束,约束一侧轴向位移,过盈连接表面设置接触对。圆管有限元模型,直径为277.10 mm,过盈量1.10 mm,如图4模拟分析发现,轴向接触应力约为65.73 MPa,轴向两侧边缘稍有应力集中,最大接触应力为68.53 MPa,整体而言,接触面上的接触应力基本一致,取平均接触应力66.45 MPa。采用组合厚壁圆筒理论接触应力解[式(2)]进行计算,所得接触应力为66.55 MPa。比较有限元模型接触应力和理论模型接触应力,有限元模型误差只有0.15%,二者具有高度的一致性,可认为圆管有限元模型具有可靠性。

表1 有限元模型单元及材料参数
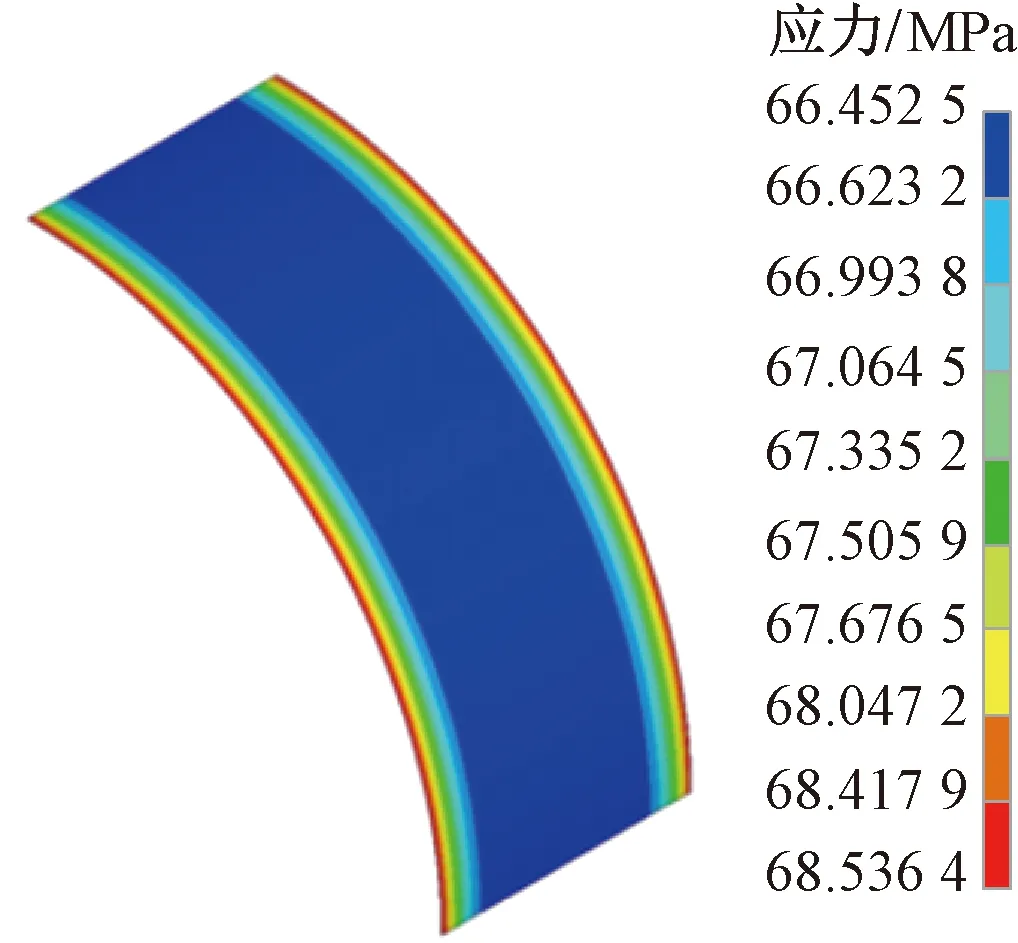
图4 圆管-连接器接触应力云图Fig.4 Contact stress nephogram of pipeline to connector
圆管模型验证有效,文章认为参数一致、问题相似、材料相同、尺寸相近的椭圆管-连接模型也是可靠的,在误差允许范围内将继续以上述两模型开展后续研究。
3 椭圆管道过盈装配应力分析
3.1 管道极值有效应力与等效过盈量的关系
海底管道由于存在直径误差和椭圆度而面临过盈装配问题,因此必须对装配过程进行应力分析。DNV-OS-F101[13]中规定管道允许存在最大直径误差2.0%、最大椭圆度3%。依据DNV-OS-F101中管体椭圆度偏差0.001 5D,选择4组等效过盈量均为0.36%、椭圆度依次为0、0.5%、1.0%、1.5%的椭圆管-连接器研究模型。分析4组模型的接触应力,图5(a)为椭圆度1.0%工况下的接触应力分布,接触应力沿轴向和环向应力分布不均匀,但是,可以观察到接触应力存在整体对称性规律。
观察x向中面(L/B=0.5)上接触应力的环向分布,如图5(b),容易发现三组椭圆管道模型接触应力关于0°~180°、90°~270°轴对称,在45°~225°、135°~315°对称轴上关于平均直径相同的圆管接触应力分布曲线反对称,其他厚度位置也有类似规律。根据反对称性性质,接触应力对面积上的积累相互抵消;所以提出平均接触应力与椭圆度无关,仅由等效过盈量决定的假设。
为进一步验证假设,选择了16组相同等效过盈量,不同椭圆度研究模型分析接触面积和接触总压力。如图6所示。
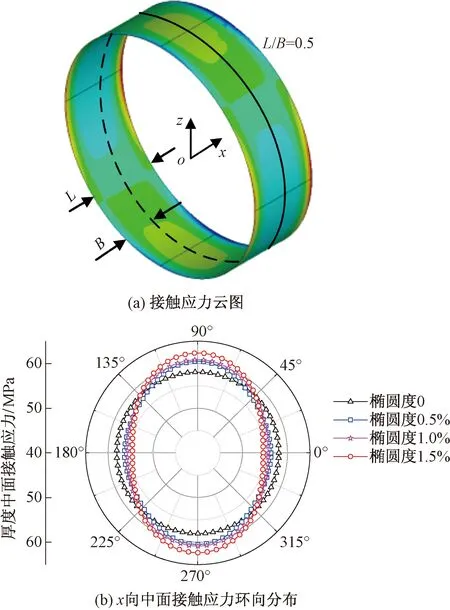
图5 管道接触应力环向分布情况Fig.5 The circumferential distribution of contact stress

图6 接触总压力及接触面积随椭圆度变化曲线Fig.6 The curve of total contact pressure and contact area with changed ovality
接触面积和接触总压力随着椭圆度增加是基本不变的,且与直径相同的圆管基本相同,根据曲线变化规律验证了平均接触应力与椭圆度无关,仅由等效过盈量决定的假设。因此可认为椭圆管道由等效过盈引起的接触应力与圆管道是相同的,结合拉梅公式得到椭圆管道最大有效应力与等效过盈量的关系式:
(6)
式(6)中:DGo为管道平均外径,即(Dmax+Dmin)/2,DGo=2b,mm;DTo为连接器外径,DTo=2c,mm;DTi为连接器内径,DTi=2a,mm;DGo-DTi=2δ,mm;EG为管道弹性模量,MPa;ET为连接器弹性模量,MPa;μG为管道泊松比;μT为连接器泊松比;t为管道厚度,mm。
观察式(6),仅考虑等效过盈量影响,椭圆管道平均接触应力与尺寸参数(过盈量、直径、壁厚、外筒内外径)和力学性能(弹性模量、泊松比)相关。
3.2 椭圆管道极值有效应力与椭圆度的关系
上述分析发现,管道与连接器等效过盈量影响平均接触应力,椭圆度会引起应力集中效应,影响分布不均匀性。因此,椭圆度也会影响修复管道的极值应力,鉴于目前并无成熟理论可参考,文章将通过数值方法分析椭圆度对管道极值应力的影响。
研究设置了等效过盈量δ分别为0.1、0.2、0.3、0.4、0.5 mm的5个系列模型,每个系列设置6组不同的椭圆度o,分别为0、0.3%、0.6%、0.9%、1.2%和1.5%,其他参数与前述模型相同。对于等效过盈量相同、椭圆度不同的模型,模拟结果显示,随着椭圆度的增加,管道最大有效应力是逐渐增加的,由环向均匀分布出现沿着大径和小径两处应力集中趋势,以等效过盈量为δ=0.1 mm的模型为例,如图7所示,椭圆管道大小径处存在应力集中的现象,并且随着椭圆度增加极值应力增加,椭圆度越大极值等效应力越大,应力集中效应越明显,承载的强度越大。
为分析椭圆度对管道极值有效应力的影响,定义椭圆度应力系数衡量椭圆度的应力集中效应。椭圆度系数为椭圆管道最大有效应力σrmax与等效过盈量相同圆管道的最大应力σrc的比值,即Ke=σrmax/σrc。如图8所示,对于等效过盈量相同的系列管道,椭圆度应力系数与椭圆度成线性增加关系,对于不同等效过盈量系列,等效过盈量越大,椭圆度应力系数增加趋势逐渐变缓。椭圆度应力系数随椭圆度是线性增加的,但是与等效过盈量成负相关。
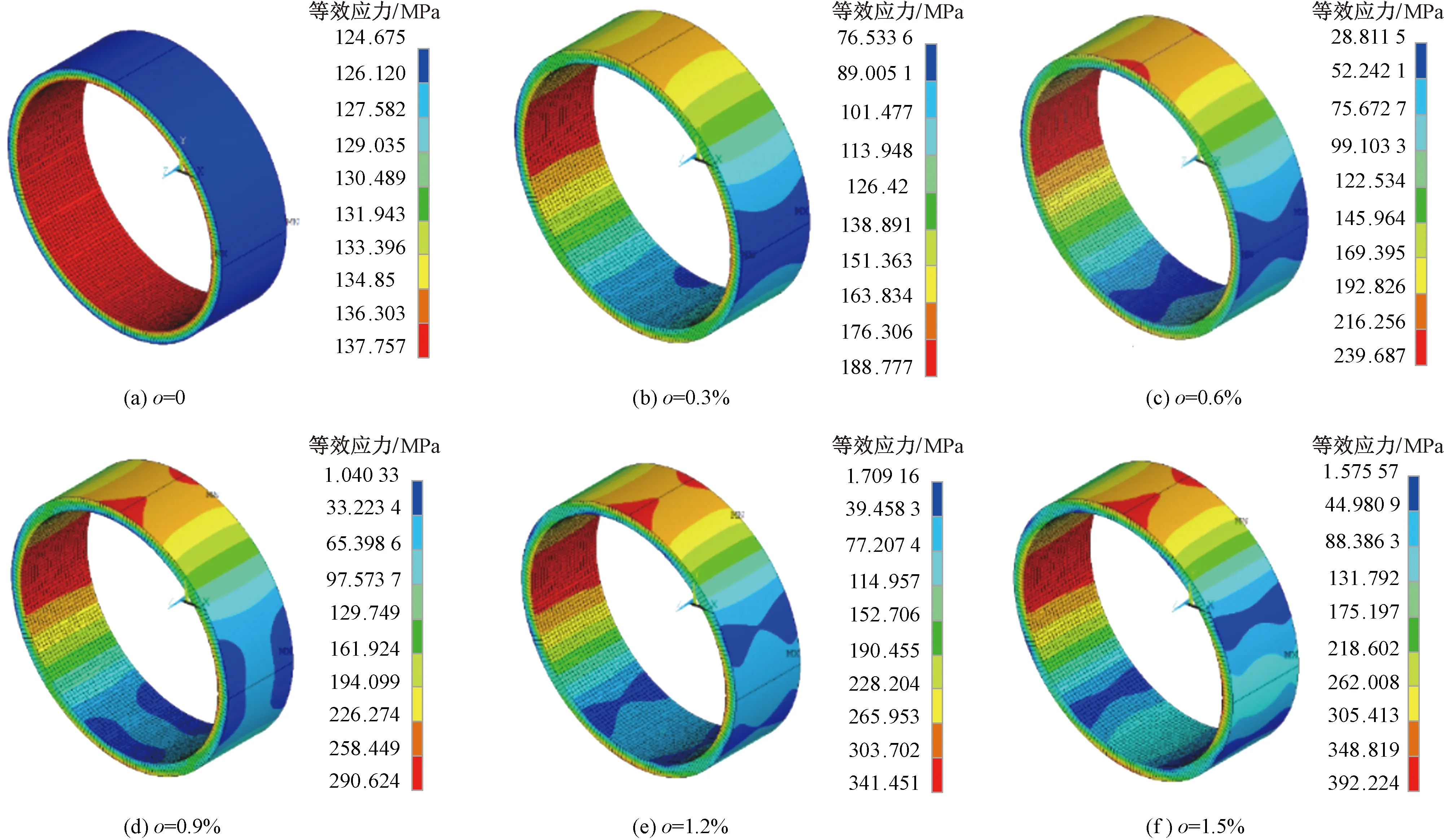
图7 等效过盈量δ=0.1 mm系列管道有效应力随椭圆度的变化Fig.7 The variation of the Von Mises stress with ovality in the equivalent interference of δ=0.1 mm
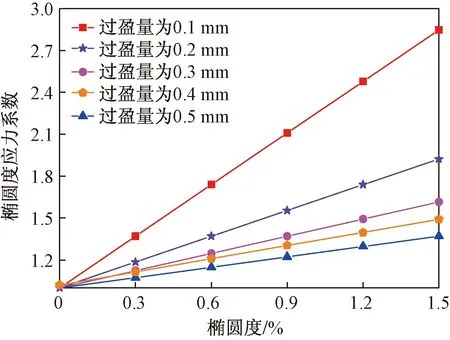
图8 椭圆度应力系数与椭圆度的关系Fig.8 Relation between the ovality stress coefficient and ovality
4 结论
将存在椭圆度的管道过盈连接问题简化为椭圆管与圆管的过盈配合模型,采用理论与数值方法对比分析的方法,验证了有限元模型简化的合理性。分析了椭圆管道和连接器过盈装配过程中椭圆度、等效过盈量对极值应力影响,得到以下结论。
(1)管道平均接触应力与等效过盈量密切相关,其大小由尺寸参数(过盈量、直径、壁厚、外筒内外径)和力学性能(弹性模量、泊松比)决定。
(2)椭圆度会影响过盈接触面上的接触应力分布均匀性,但不影响接触应力在整个过盈接触面上的作用效果。
(3)引入椭圆度应力系数衡量椭圆度的应力集中效应,对于等效过盈量相同的系列管道,椭圆度应力系数与椭圆度成线性增加关系,对于不同等效过盈量系列,等效过盈量越大,椭圆度应力系数增加趋势逐渐变缓。
(4)随管道椭圆度增加,适当增加等效过盈量。即可增大过盈装配过程中管道承载的强度。
