管桩预应力自动张拉机张拉部件的优化设计与疲劳寿命分析
2020-11-10杜卫东龚发云李飞扬
汤 亮, 杜卫东, 龚发云, 李飞扬
(1.湖北工业大学机械工程学院, 武汉430068; 2.湖北省制造业创新方法与应用工程技术研究中心, 武汉430068)
预应力混凝土技术在建筑结构等领域应用非常广泛[1-2]。管桩预应力张拉机是一种预应力管桩生产的主要设备,它为管桩钢筋笼施加预应力,保证管桩获得良好的力学性能和产品质量。随着城镇化的加速,对预应力混凝土产品的质量和产量有越来越高的要求。实践表明,管桩生产过程中,张拉机长期处于频繁启动、制动以及重复变幅载荷的状态,长期反复的重载荷作用可能引起机械系统故障,甚至导致零部件疲劳失效,严重影响管桩产品的质量,给企业带来巨大的安全隐患和经济损失[3-4]。近年来,在预应力张拉机设计方面有一些研究。任磊[5]为了减少轨道板的裂纹,增加轨道板的使用寿命,对张拉部件进行了有限元分析,设计了高铁轨道板预应力筋自动张拉。刘瑞东[6]设计预应力水泥电杆张拉机,提高了水泥张拉生产自动化程度,保证了张拉的准确度。在张拉部件优化和疲劳寿命预测的研究较少,因此为了有效地降低张拉部件疲劳断裂引起的安全事故的发生率,和保障工作人员生命以及财产安全,对优化设计方案进行疲劳寿命预测显得至关重要。
疲劳寿命预测方法一直是机械装备设计领域研究的热点[7-9]。由于实际零件的载荷多为变幅载荷,其具有随机性且难以准确获取,为了分析变幅载荷的疲劳寿命,学者们提出了一些变幅载荷疲劳寿命预测的方法。有的学者提出了理论模型,进行变幅载荷疲劳寿命预测。徐国建等[10]根据Miner理论,通过对恒幅载荷条件下应力幅与寿命之间的关系的随机化处理,提出了用于随机变幅载荷下疲劳可靠性分析的RDCDR模型。赵少汴[11]根据Miner理论简化实际零件受到的变幅载荷,只认为峰值和谷值对寿命起作用,将变幅载荷看作是若干个恒幅载荷的组合。也有的方法是基于实验进行变幅载荷的疲劳寿命预测。Sonsino等[12]通过对比试验,研究了变幅载荷与恒幅载荷的疲劳寿命,得出变幅载荷疲劳寿命高于峰值的恒幅载荷疲劳寿命,因此施加恒幅载荷得到的寿命结果较为保守。卢耀辉等[13]通过车辆系统动力学计算获得车体随机载荷谱,基于FKM标准和有限元法对高速列车进行疲劳寿命分析。还有的方法是基于有限元分析进行变幅载荷的疲劳寿命预测。卢黎明等[14]利用ABAQUS动力学仿真分析结果生成变幅载荷谱,基于nCode Design-Life对滚滑轴承疲劳寿命进行了预测。
现以提高系统的响应速度为目标对张拉部件进行轻量化设计;根据Miner理论简化实际零件受到的变幅载荷,通过将变幅载荷转化为峰值的恒幅载荷来分析其疲劳寿命;由易损伤点位置的分析进一步明确了优化方案,并对比分析了优化前后的疲劳寿命。与传统实验法进行疲劳寿命分析相比,此方法缩短了前期设计周期以及为进一步优化设计提供一定的安全空间,是一种高效实用的方法。
1 张拉部件结构优化设计
1.1 张拉部件结构设计
管桩预应力自动张拉机整体方案如图1所示,主要由管径检测传感器、锁螺母装置、张拉部件、千斤顶、垂直升降台、控制柜和水平位移小车组成。管桩预应力自动张拉机的基本工作原理:张拉机自动调整位置与管桩模对接,其千斤顶活塞收缩将预应力传递给管桩模内部的钢筋笼。考虑到张拉机使用环境和功能要求,其执行端部件主要完成自动对接和张拉两个动作,因此设计了合抱式张拉部件。张拉部件主要包括卡爪、位置传感器1、张拉杆、液压缸、转轴、位置传感器2、基座和拉杆。张拉部件具体结构如图2所示,张拉机对接和张拉过程中,首先张拉杆接触到位置传感器1产生限位信号,两个液压缸推动两个卡爪合抱张拉杆;接着两个卡爪合拢时触发位置传感器2产生信号,表明对接已完成;最后液压千斤顶活塞收缩,通过张拉部件将预应力传递给管桩模内部的钢筋笼。
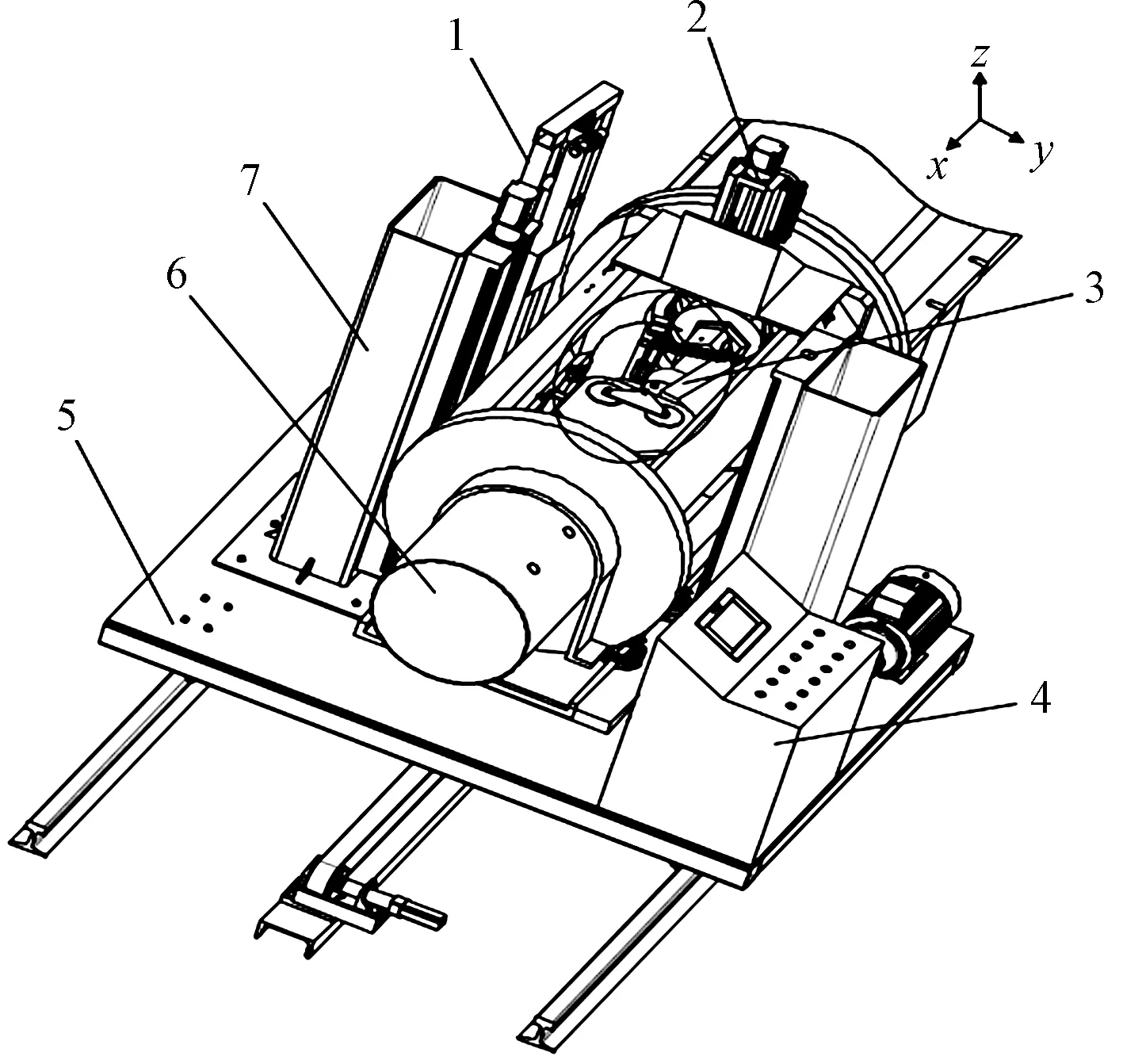
1为管径检测传感器;2为锁螺母装置;3为张拉部件;4为控制柜;5为水平位移小车图;6为千斤顶;7为垂直升降台图1 管桩预应力自动张拉机整体方案Fig.1 The general scheme of prestressed pipe automatic tensioning machine

1为位置传感器1;2为卡爪;3为位置传感器2;4为液压缸;5为基座;6为拉杆;7为转轴;8为张拉杆图2 张拉部件结构示意图Fig.2 Structural sketch of tensioning components
1.2 活动零件卡爪的静力学分析
张拉部件是管桩预应力张拉机的重要执行端,其中卡爪是关键的执行零件,卡爪的力学性能与张拉部件的寿命有密切关系,因此有必要进行静力学分析。E级钢是广泛应用于火车车钩的材料,其各项强度几乎是45钢的2倍,因此,采用E级钢可以更好地提升张拉部件整体的工作性能[15-17]。根据卡爪使用的要求,分析得到卡爪主要承受拉力,因此利用第一强度理论分析计算得出初始尺寸。在Solidworks中建立卡爪的三维模型,导入到ANSYS Workbench中,定义卡爪的材料属性为E级钢,其弹性模量E=2.15×1011Pa,泊松比为0.3,密度为7 050 kg/m3。采用四面体单元Solid186将模型进行网格划分。张拉机在张拉过程中最大的张拉力为300 t,每一个卡爪受到的拉力最大为1 470 kN,因此在卡爪一端设置固定约束,另一端施加大小为1 470 kN的拉力,得到卡爪的加载模型,如图3所示。有限元模型进行求解可以得到卡爪应力云图,如图4所示。

图3 卡爪有限元模型Fig.3 Finite element model of connector
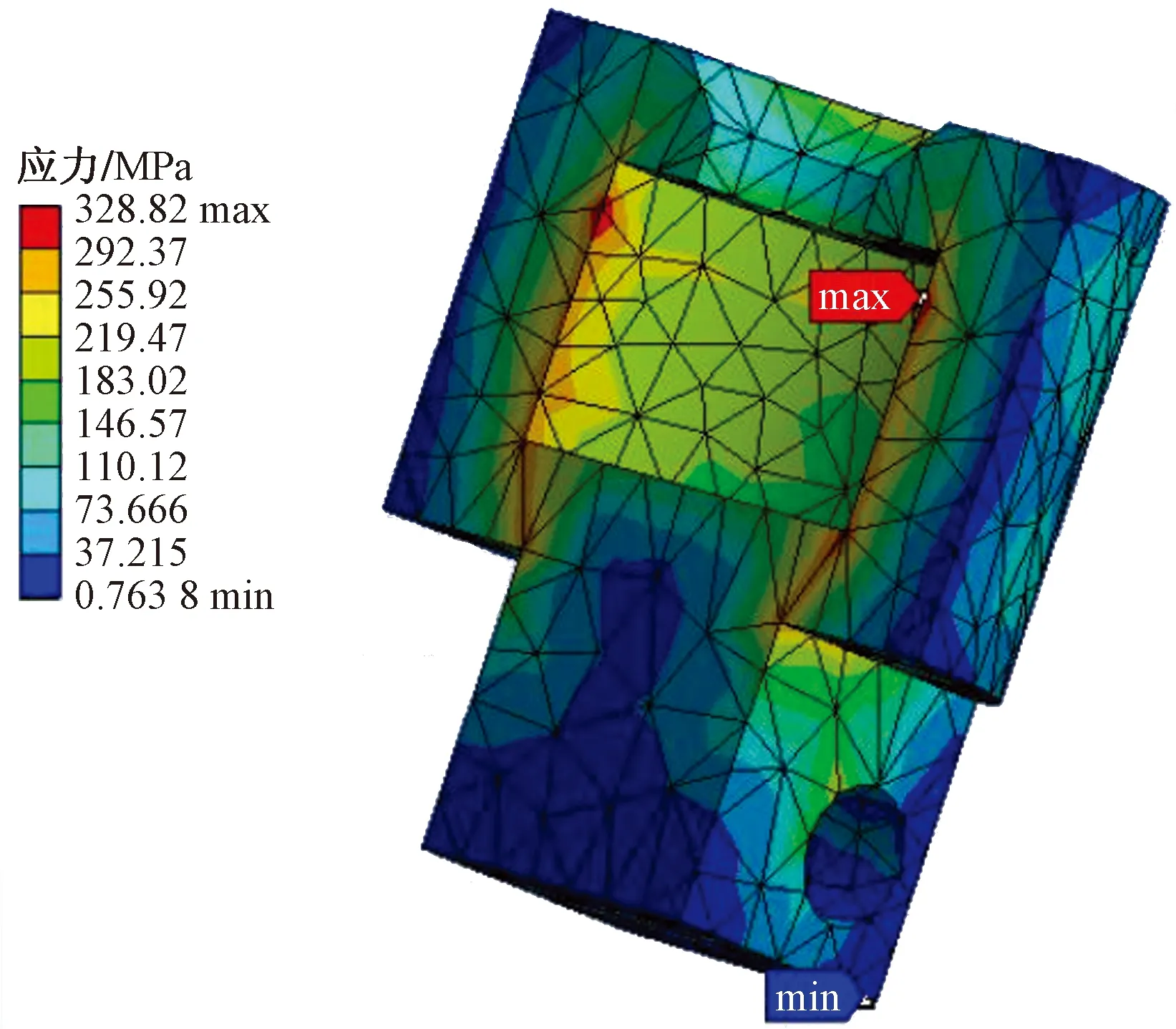
图4 卡爪应力云图Fig.4 Stress nephogram of connector
由有限元求解结果可知,活动零件卡爪的最大应力为328.82 MPa,小于材料的屈服极限690 MPa,满足其强度要求,其质量有较大的盈余,惯性过大,不利于执行机构的控制,严重影响了张拉执行系统响应的速度,因此活动零件卡爪必须进行轻量化设计。
1.3 卡爪尺寸优化设计
根据张拉部件的工作和装配要求,选取卡爪截面尺寸D1、D2、D3、L1作为优化设计变量X。卡爪的结构特点可知,可以将以质量最小为目标简化为以剖面的面积S最小为优化目标,ε为最大变形量,σmax为最大应力,可以得到尺寸优化数学模型,如图5所示。
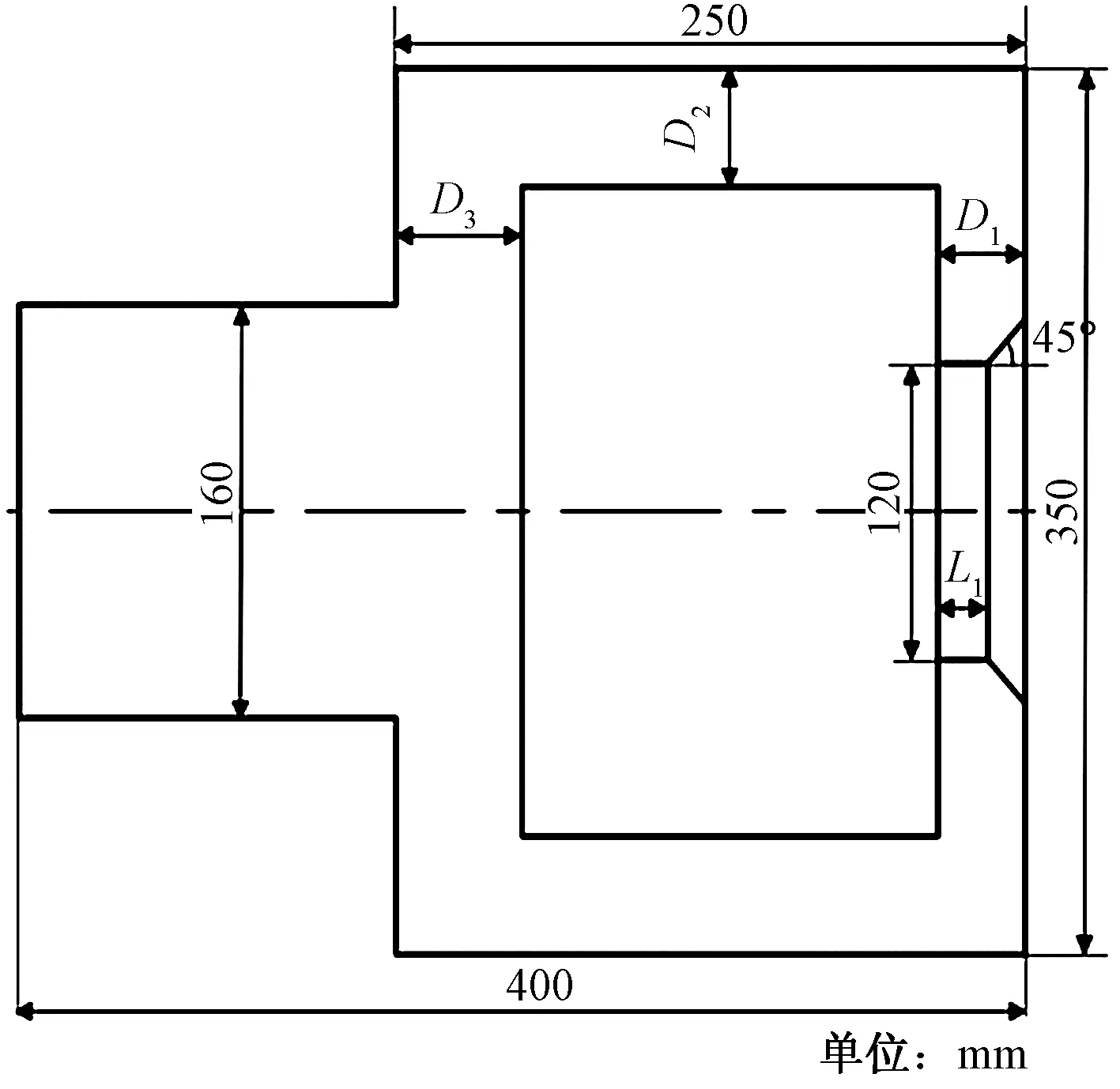
图5 尺寸优化数学模型 Fig.5 Mathematical model of size optimization
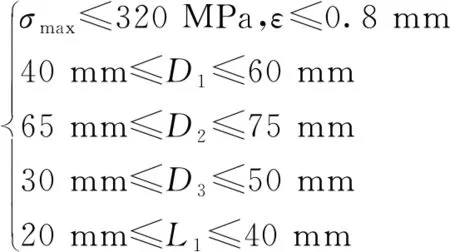
根据活动执行端卡爪的活动空间范围及其强度与刚度要求,确定优化的约束条件为
X=(D1,D2,D3,L1)T,
minS=24 000+350D1+500D2+350D3-
2D2(D1+D3)-120L1-(D1-L1)2,
(1)
由活动零件卡爪优化数学模型可知,约束函数是设计变量的隐函数,因此其优化算法必须结合有限元分析才能进行优化求解。利用ANSYS Workbench中的Goal Driven Optimization模块,基于有限元分析结果的响应曲面算法,采用Kriging法能够准确高效地得到上述卡爪优化数学模型中隐函数的解集。以卡爪截面尺寸D1、D2、D3、L1作为输入变量,根据边界条件,输入变量D1取40~60 mm,D2取65~75 mm,D3取30~50 mm,L1取20~40 mm,以卡爪的质量m、最大应力σmax、最大变形量ε为输出变量,并设置面积最小为目标函数,以σmax<320 MPa、ε<0.8 mm为约束条件,Workbench给出3组最佳的优化解,如表1所示。
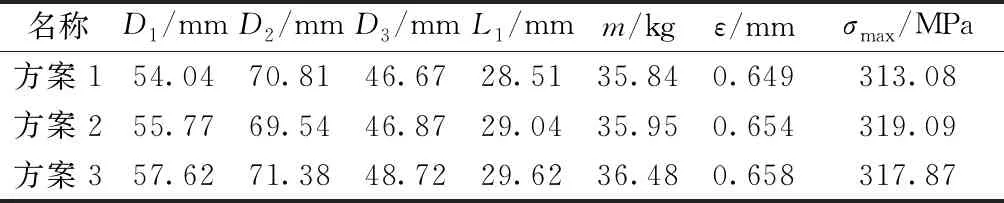
表1 最佳的优化解
综合考虑卡爪轻量化与强度刚度要求,选择方案1为最优设计方案,将方案1进行圆整,即取D1=54 mm、D2=70 mm、D3=46 mm、L1=28 mm,作为最终优化方案。最终优化方案进行静力学分析,结果如表2所示。
利用拓扑优化的分析,结果如图6所示,得出卡爪质量还有较大的盈余,同时考虑到其执行动作时的干涉问题,于是卡爪结构进一步优化,即圆角处理。

表2 优化前后结果对比
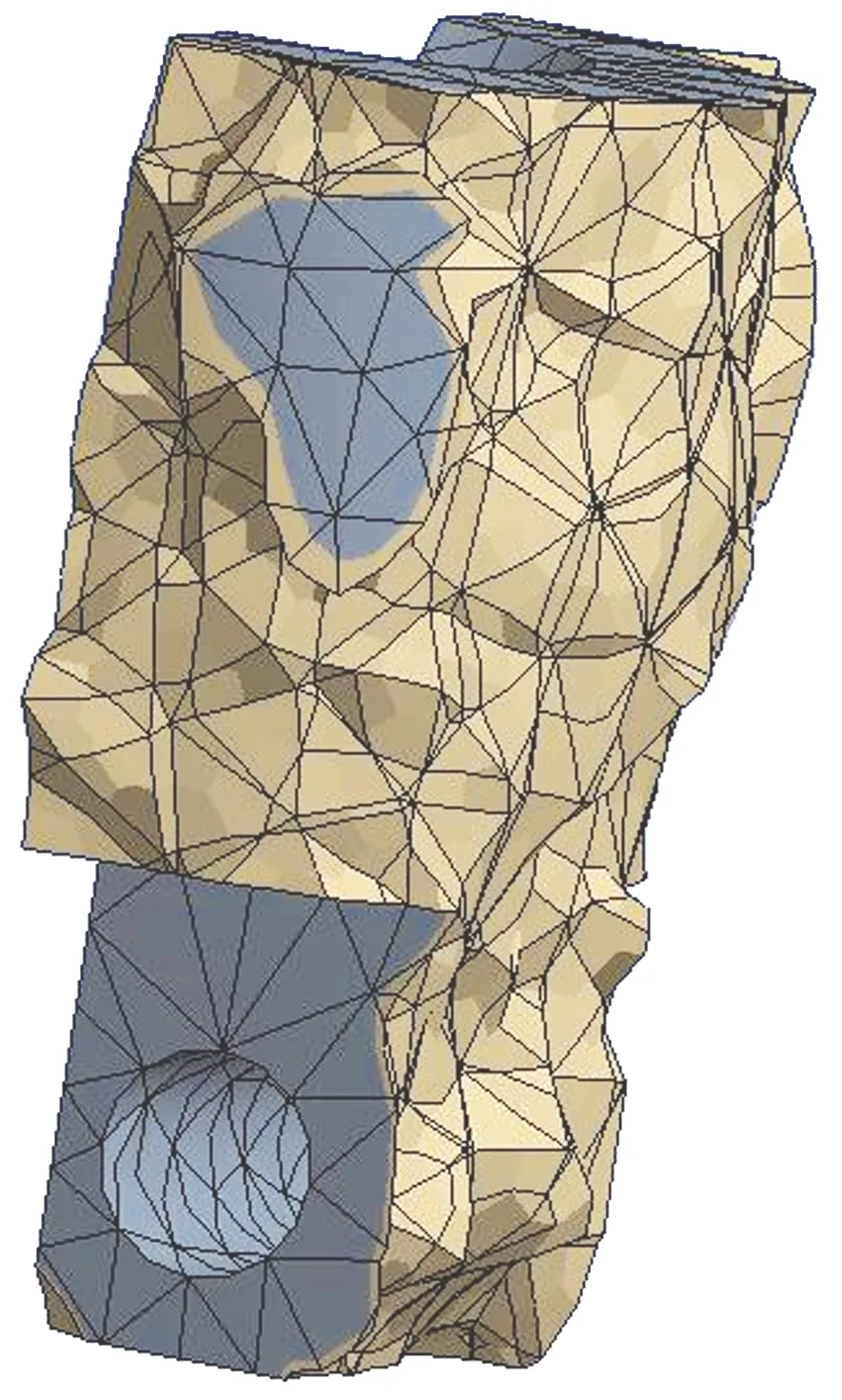
图6 拓扑优化 Fig.6 Topological optimization
得到优化结果:图7为再优化有限元模型,图8为再优化应力云图。由图7、图8可以得到,最大应力为219.69 MPa,远远小于材料的屈服强度。最终质量为33.524 kg,质量总体减少了16.75%,从而减少了执行系统的惯性力,提高了响应速度,提高了张拉机的工作性能。
2 张拉部件静力学分析
2.1 建立张拉部件有限元模型
考虑到张拉部件实现的功能和强度要求,分析各个零部件的受力情况,根据不同的受力情况分别采用第一强度理论和第三强度理论分析计算得出零部件的重要尺寸,结果如表3所示。
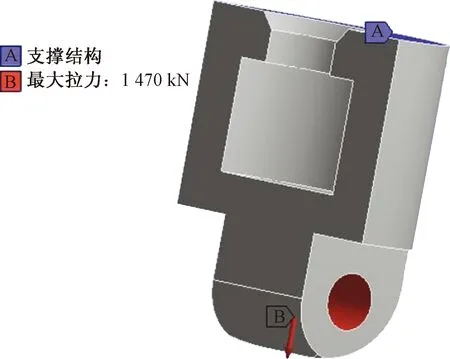
图7 再优化有限元模型Fig.7 Reoptimization finite element model
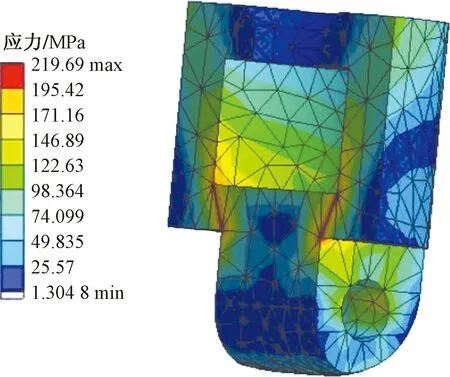
图8 再优化应力云图Fig.8 Re-optimizing stress nephogram
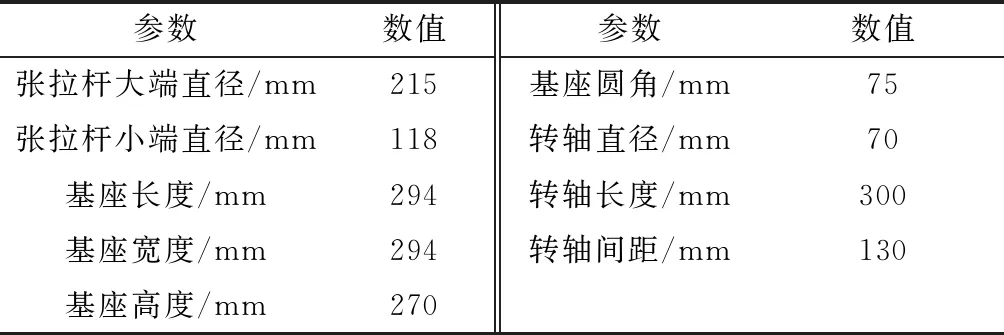
表3 张拉部件主要参数
为了真实有效地反映其疲劳损伤和疲劳寿命情况,采用整部件模型分析,转轴与基座采用刚性连接,卡爪与转轴采用铰关节连接,并考虑到卡爪与张拉杆的紧扣连接。为了便于有限元分析,需要将结构简化,因此可以忽略影响较小的因素,利用表3中的数据建立张拉部件有限元简化模型,结果如图9所示。在预应力张拉时,两卡爪处于完全闭合状态,张拉力是沿Z轴方向,考虑到在此状态下张拉部件承受全部的张拉力300 t。张拉部件结构分析计算主要需要考虑的载荷类型是张拉工作载荷,其峰值为最大张拉预应力2 940 kN,因此以最大张拉预应力为承受载荷进行静强度分析。
在ANSYS Workbench中进行有限元静力学分析,采用四面体单元网格划分,完整的卡爪、转轴、基座和后张拉杆网格划分,网格划分结果如图10所示,单元最小尺寸为10 mm,包含单元数67 062个,节点数116 118 个。

图9 张拉部件有限元简化模型 Fig.9 The simplified finite element model for tension parts

图10 张拉部件网格划分结果Fig.10 Meshing results of tensioning parts
2.2 张拉部件静强度分析
通过有限元分析得到应力云图,如图11所示。

图11 张拉部件应力云图Fig.11 Stress nephogram of tensioning parts
从有限元分析结果得出,最大应力为425.71 MPa,远小于材料的屈服极限强度690 MPa,位于卡爪形状突变位置和张拉杆的轴肩处,并且在最大应力附近的应力分布梯度较大,应力集中非常显著。
3 张拉部件疲劳分析
3.1 获取载荷时间序列
张拉部件作为张拉机的重要执行端,长期承受重复变幅载荷,是常常疲劳破坏的部件。依据ANSYS Workbench静力分析结果得到最大应力小于屈服极限强度,以及疲劳类型分类,确定该张拉部件属于应力为主导的高周疲劳类型,因此选择应力疲劳(S-N)分析方法[18]。基于ANSYS Workbench有限元静力学分析结果,利用总应变寿命方程基本原理和Miner理论,采用nCode Design-Life专业疲劳寿命仿真分析软件[19],对张拉部件进行疲劳寿命预测。
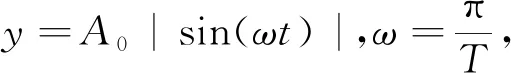
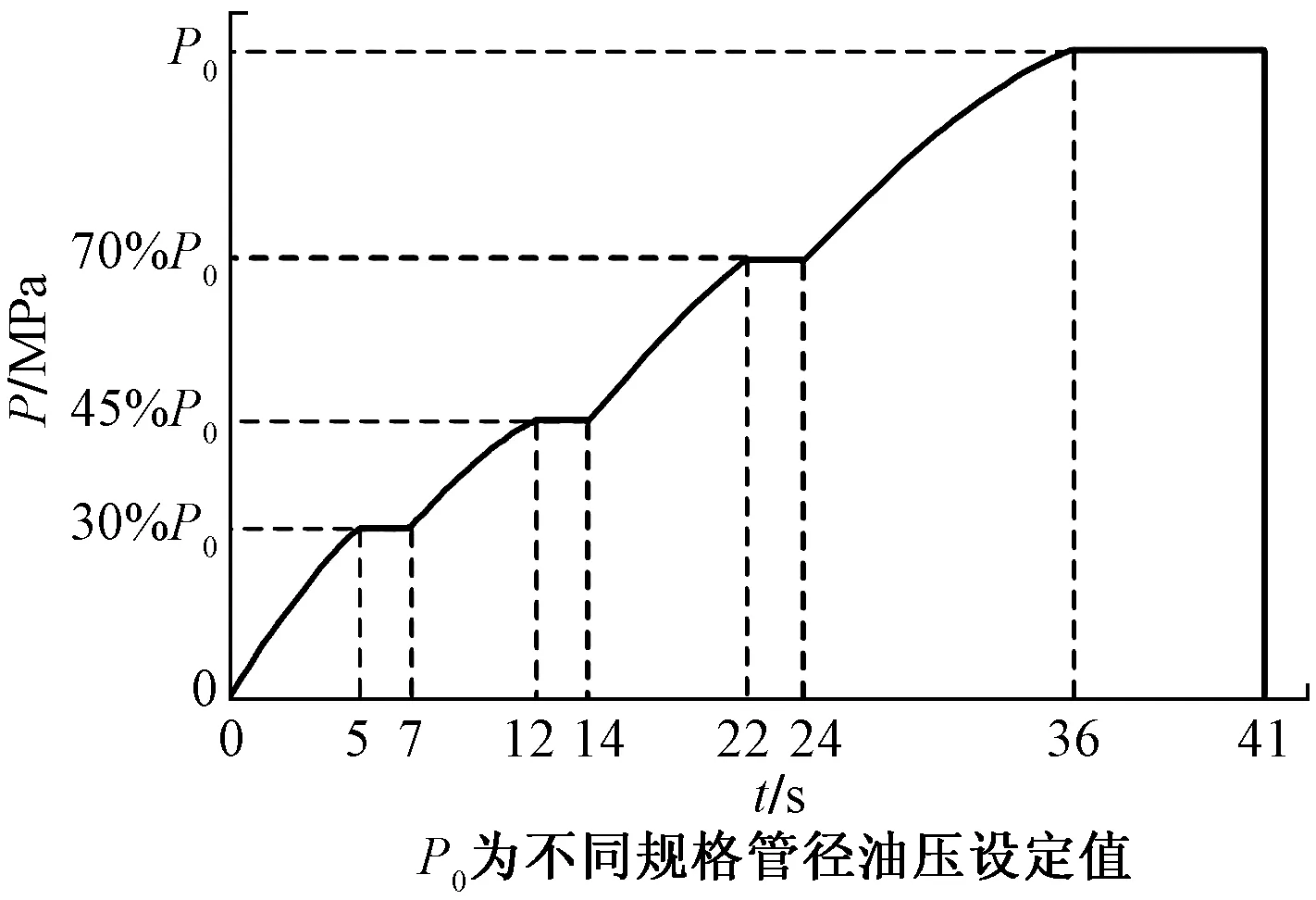
图12 张拉曲线的加载阶段Fig.12 Loading stage of tension curve
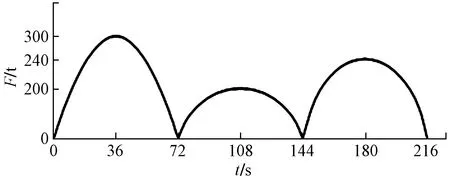
图13 简化后的张拉载荷Fig.13 The simplified tension load
载荷时间序列反映了零部件所受载荷随时间的变化情况,其与静载荷结果相映射作为疲劳寿命分析的循环载荷谱。根据张拉机的载荷范围和拟合的张拉曲线,需要确定最大值的恒幅载荷时间序列。以最大峰值300 t为例编制载荷时间序列,0.1 s间隔为步长,利用MATLAB编制计算程序,得到载荷时间序列文件。将载荷时间序列文件输入nCode Design-Life中,绘制得到一个作业循环的载荷时间序列曲线,如图14所示。
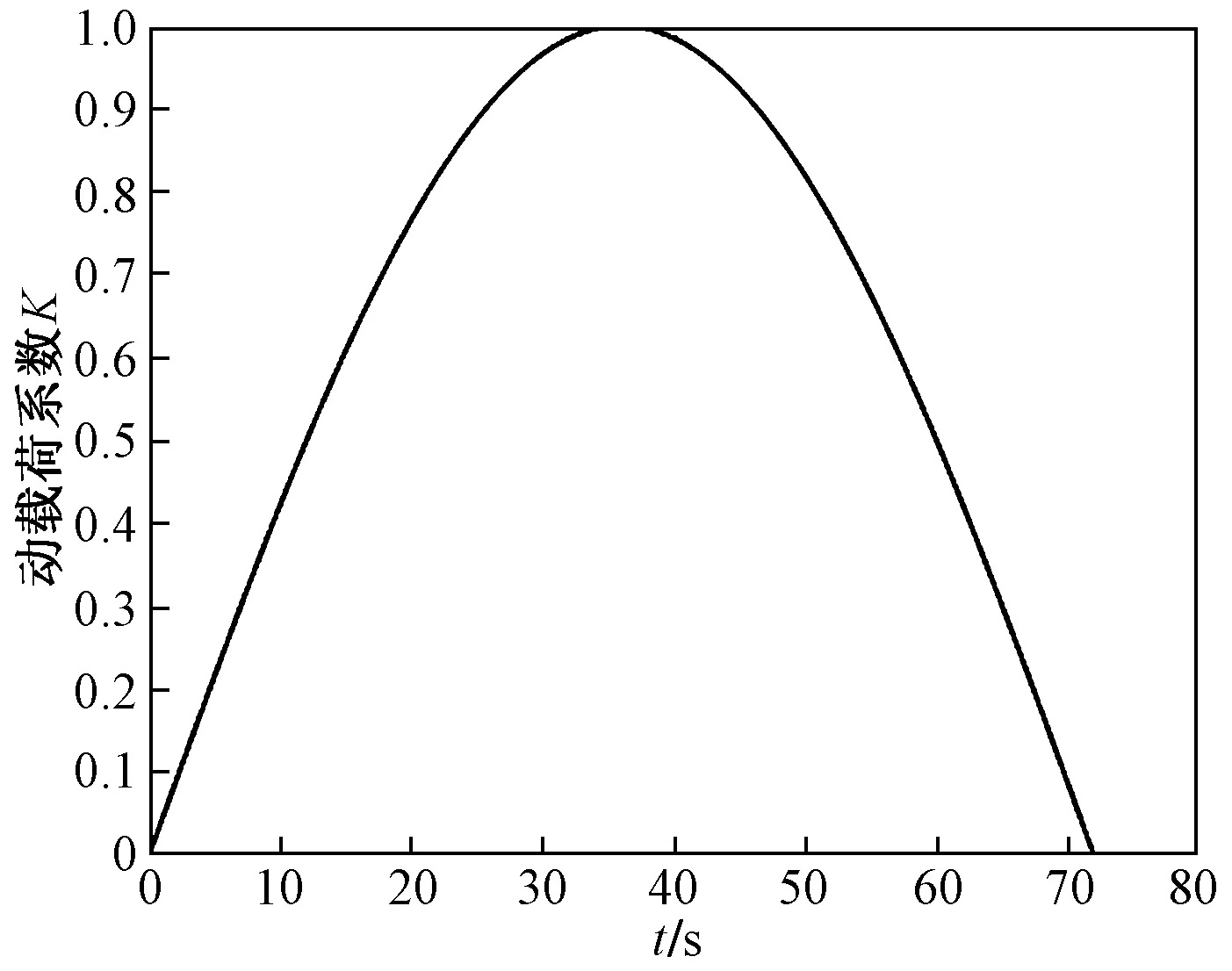
图14 300 t载荷时间序列曲线Fig.14 Time series curve of 300 tons load
3.2 材料设置
为了精确地预测疲劳寿命,必须保证材料参数的准确性。该张拉部件所用材料均采用屈服强度为690 MPa的E级钢。国家标准提供的材料寿命参数是通过标准试棒测得的数据,实际零件与标准试棒的形状差别较大,以及考虑到使用环境和载荷状况等多种影响因素,需要将材料寿命数据进行等效处理,因此对标准的S-N曲线进行修正,才可以进行精确的疲劳寿命计算。采用Soderberg理论进行修正,得到材料修正后的S-N曲线,结果如图15所示。

图15 修正后S-N曲线Fig.15 The corrected S-N curve
3.3 疲劳预测分析
将ANSYS workbench静力学的分析结果与nCode Design-Life连接进行联合仿真,创建材料和载荷谱的映射,设置求解参数,利用有限元计算得出疲劳损伤云图和寿命云图。最大峰值恒幅载荷疲劳寿命云图和损伤云图,如图16、图17所示。
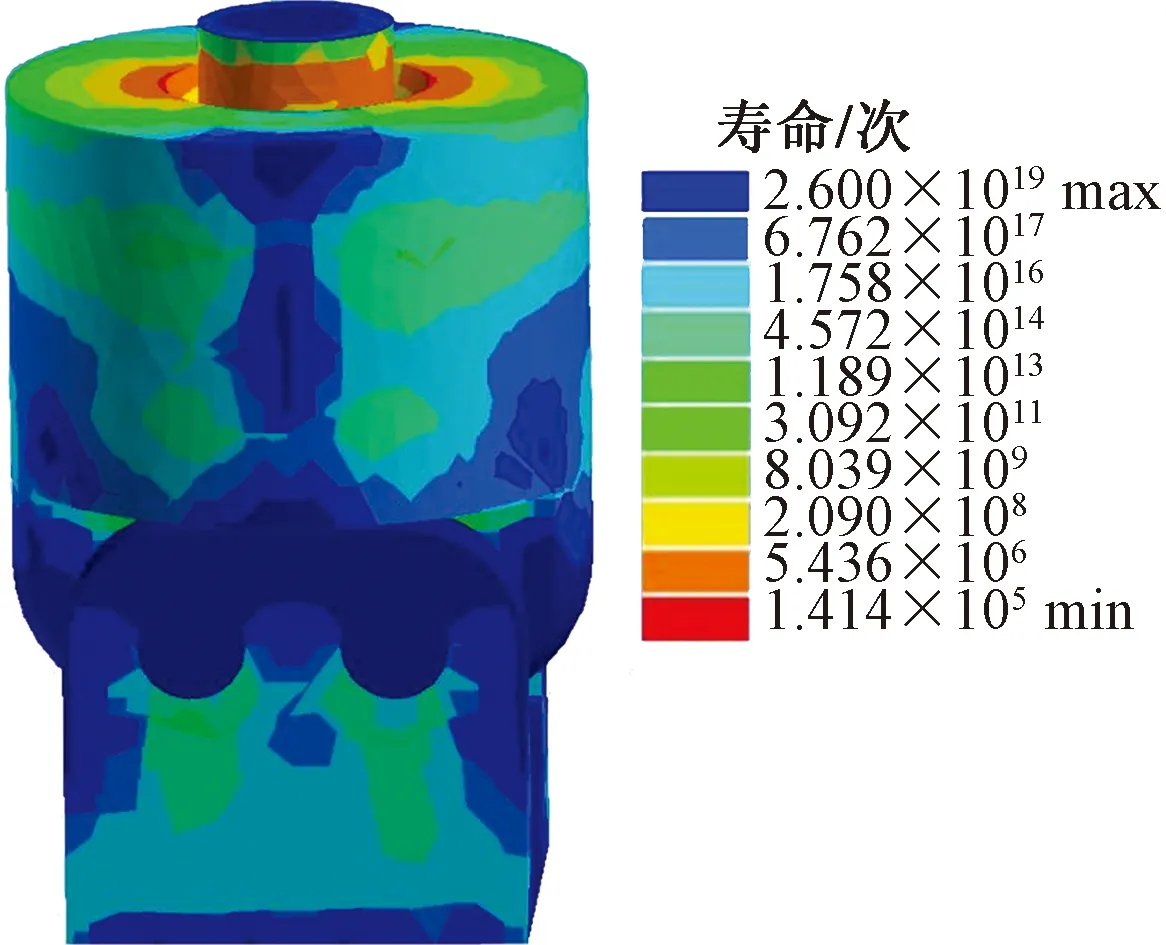
图16 最大峰值恒幅载荷疲劳寿命云图 Fig.16 Fatigue life nephogram of maximum peak constant
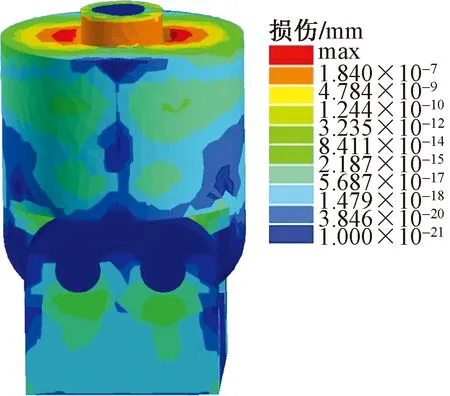
图17 最大峰值恒幅载荷疲劳损伤云图Fig.17 Fatigue damage nephogram of maximum peak constant
根据图16、图17,考虑到生产效率和8 h工作制,以及张拉机准备时间得出每月循环次数为4 000 次,进而计算出张拉部件的寿命。在变幅载荷作用下,张拉部件绝大多数部位循环次数均大于1.77×105次,最大损伤值为7.07×10-6mm,疲劳循环次数为1.41×105,其寿命为2.95年。
3.4 最易损伤位置分析
通过在nCode Design-Life中的glyph区域中添加hot模块,可以得到最伤点位置及其损伤情况,如表4为在最大峰值恒幅循环载荷条件下10个最易损伤点的疲劳寿命情况。
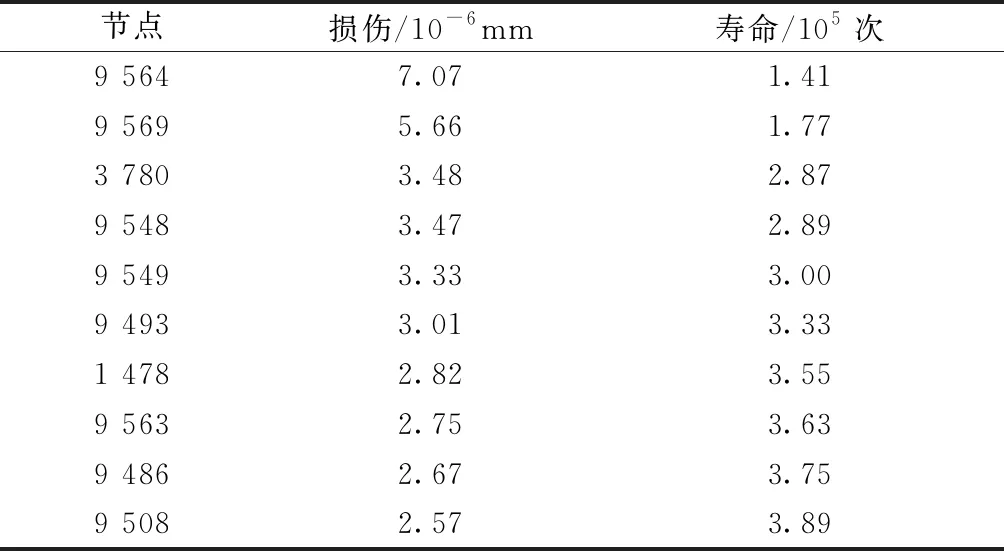
表4 疲劳损伤最大节点处疲劳寿命及损伤大小
4 张拉部件再优化以及寿命预测分析
机械结构的变截面处,在外部载荷作用下往往会出现应力集中, 易出现疲劳失效[20]。通过易损伤位置的分析,针对张拉部件的连接处应力集中问题,得出在连接处极易产生裂疲劳纹和破坏,因此提出了在卡爪和张拉杆的应力集中处增大圆角以提高张拉部件疲劳强度的方法,如图18所示。

1为卡爪;2为张拉杆;3为圆角处图18 卡爪与张拉杆连接处增大圆角处理Fig.18 Increased the roundness at the joint of connector and tensioning rod
通过表4确定张拉部件的易损伤位置,可以为在包括材料等其他基本因素相同的条件下建立有限元模型,以载荷峰值300 t为例,利用ANSYS Workbench中进行静力学分析,结果如图19所示。圆角前后结果对比如表5。由应力云图可知最大应力为388.91 MPa,与结构优化前相比最大应力减小了,并且最大应力节点附近应力分布梯度较小,因此应力集中有了明显改善。根据上述的疲劳分析流程图以及载荷时间序列曲线,基于结构优化后的静力学分析结果进行疲劳寿命分析,结果如图20所示。
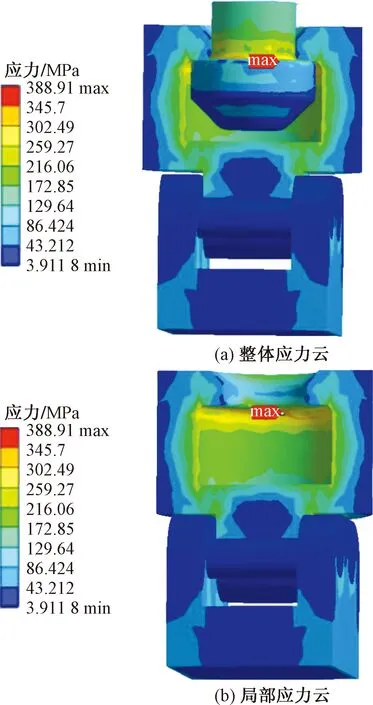
图19 张拉部件结构再优化应力云图Fig.19 Stress nephogram of re-optimizing structure of tensioning parts

表5 圆角前后结果对比
分析最大峰值恒幅循环载荷疲劳寿命云图可知,在载荷作用下循环次数为1.78×105次,因此该张拉部件的寿命为3.41年,比优化前的疲劳寿命提升了15.5%。通过对比优化前后的疲劳寿命,得到采用大圆角的方法可以改善应力集中的状况,以及提高疲劳强度,为新一代张拉部件优化设计提可靠的理论依据。
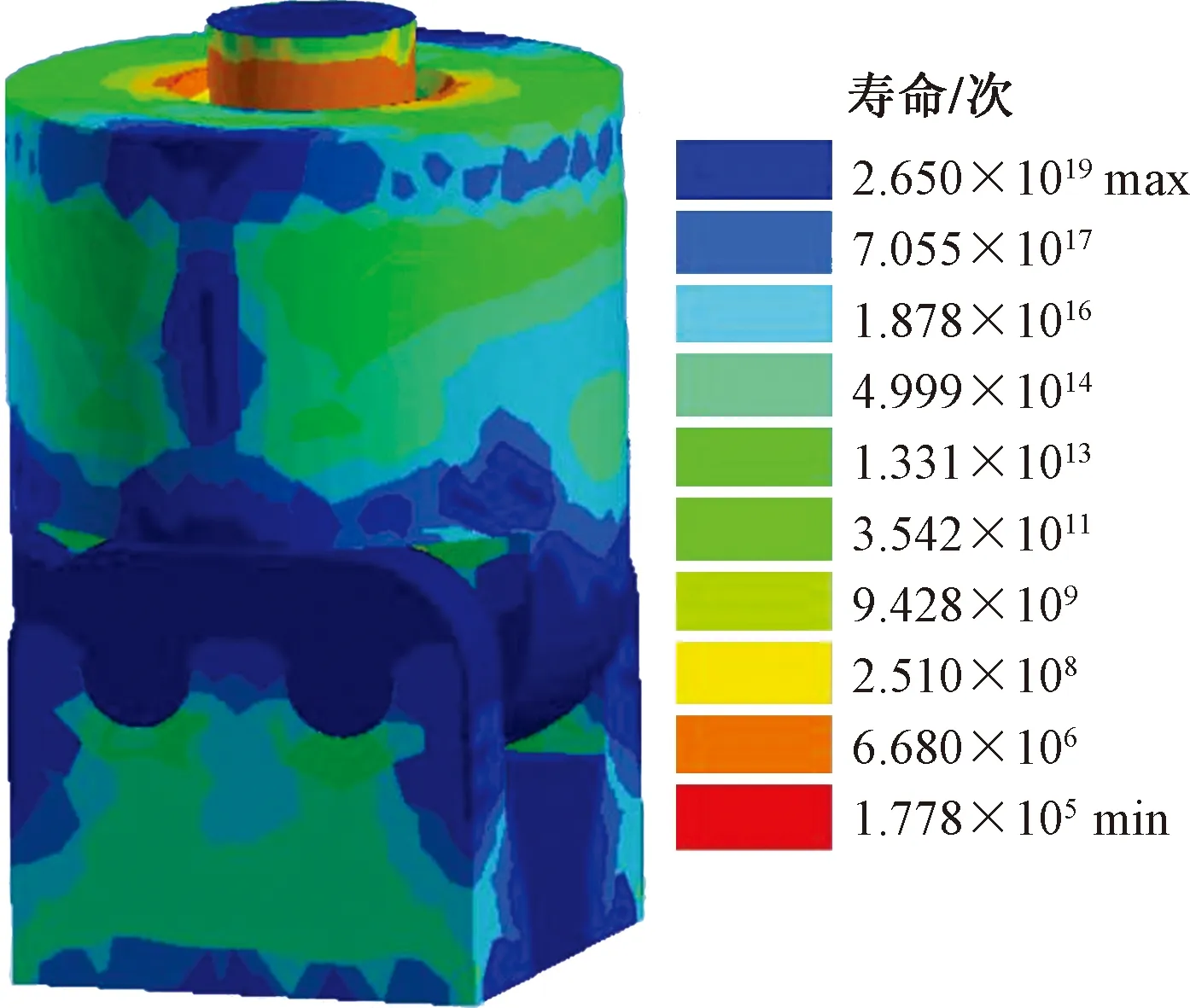
图20 张拉部件结构再优化寿命云图Fig.20 Life nephogram of re-optimizing structure of tensioning parts
5 结论
(1)为了解决张拉机笨重导致加载滞后时间过大的问题,设计了合抱式张拉部件,同时对活动零件卡爪进行了优化设计与轻量化设计,改善了张拉机的工作性能,为新一代张拉机的设计制造提供了思路。
(2)基于有限元静力学分析结果,利用nCode Design-Life疲劳仿真软件建立疲劳分析流程图,将变幅载荷转化为峰值的恒幅载荷条件来进行疲劳寿命预测,分析张拉部件损伤云图和寿命云图,从而得出变幅载荷条件下张拉部件的疲劳寿命范围。与传统实验法进行疲劳寿命分析相比,此方法缩短了设计周期和减少了成本。
(3)张拉机关键执行端张拉部件受到的变幅载荷具有随机性,其疲劳寿命具有较大的离散性,且在前期优化设计中变幅载荷曲线难以准确获取,基于峰值的恒幅载荷疲劳寿命结果较为保守,利用钢筋拉伸曲线将变幅载荷转化为最大峰值的恒幅循环载荷条件下的疲劳寿命预测,利用这一结果为零部件优化设计预留安全空间,可以为张拉部件的设计提供参考。
