The effect of resonant magnetic perturbation with different poloidal mode numbers on peeling-ballooning modes

Liangkang DONG(董良康),Shaoyong CHEN(陈少永),Maolin MOU(牟茂淋) and Changjian TANG(唐昌建)

1 College of Physics,Sichuan University,Chengdu 610065,People’s Republic of China

2 Key Laboratory of High Energy Density Physic and Technology of Ministry of Education,Sichuan University,Chengdu 610065,People’s Republic of China

Abstract

Keywords:tokamak,resonant magnetic perturbation,edge-localized mode,peeling-ballooning modes,pedestal

1.Introduction

High-confinement mode(H-mode)has been determined to be the most promising operation in future nuclear fusion devices,such as the International Thermonuclear Experimental Reactor(ITER)[1-3].It has been found that H-mode is normally accompanied by the occurrence of a steep edge gradient of pressure(pedestal),which can drive a specific magnetohydrodynamic(MHD)instability,the so-called edge-localized mode(ELM)[4].The ELM can release energy and particles from the plasma edge,causing overloaded heat on the divertor[5].However,it helps to expel impurities[4].As a result,it is necessary to mitigate or suppress type I ELM and develop a small ELM H-mode.

Externally applied resonant magnetic perturbation has been one of the main methods to control ELM in recent decades.There are many experiments on ELM mitigation and suppression by RMP with various modes.In both the low[6]and high[7]collision conditions,ELMs are eliminated with RMP in DIII-D.Recent experiments[8]in DIII-D show that ELMs are partly suppressed,and there are only some residual grassy ELMs with n=3 RMP.ASDEX-Upgrade[9],KSTAR[10]and EAST[11]also successfully suppressed ELM with n=2 and n=1 RMPs,respectively.In JET[12]and MAST[13,14],n=1 and n=4 RMPs are used for mitigating ELM.To explain the mechanism involved in ELM mitigation by RMP,a series of simulations on ELM mitigation[15-18]and suppression[19-21]have been developed.Champman et al have shown that RMP can change edge rotation,the 3D corrugation of the plasma boundary and lead to the existence of lobe structures,which reduce the pressure gradient threshold of peeling-ballooning(P-B)mode instability,thus the pedestal can be re-established to the threshold faster after an ELM crash,resulting in ELM mitigation[16].Bécoulet et al have shown that RMP can drive mode coupling in the nonlinear phase,which can produce small multimode relaxations instead of a large ELM relaxation due to the most unstable medium-n ballooning mode[15].

Although the mechanisms above have been proposed to explain the mitigation of ELM,these mechanisms do not explain the phenomena of how the ELM mitigation effect changes with RMP modes.It is necessary to explore the mechanism and relation between mitigation effect and RMPs with different modes because it may help us understand the ELM mitigation.

In recent decades,type I ELMs have been successfully explained by P-B mode theory in the pedestal[22],whereby the strong bootstrap current drives peeling modes and the steep pressure gradient generates ballooning modes.In this work,RMPs with different resonant surface locations are used to affect the P-B modes.This simulation is based on BOUT++MHD code[23-25].To consider different resonant surfaces,the poloidal mode numbers are set to be m=5,6,7,while the toroidal mode number of RMP is n=3.Changes in the effects of RMP on the P-B modes,when using different m/n RMP modes,are preliminarily studied in this work.The remainder of this paper is organized as follows:section 2 describes the physics model and section 3 represents the simulation results and analysis,section 4 is the conclusion and discussion.

2.Physics model

In order to simulate the P-B mode instability,four-field reduced MHD BOUT++code[26]is used.The evolutions of vorticity,parallel velocity,pressure and magnetic potential are shown in equations(1)-(4):

Figure 1.Vacuum field of resonant magnetic perturbation(m/n=7/3)in the poloidal section.

where H is an amplitude modulation factor.Cpeak=0.5,W=0.3 are the Gaussian peak and broadening in the poloidal angle,respectively.Figure 1 is the vacuum field of RMP(m/n=7/3)in the poloidal section.

In this simulation,we adopted a field-aligned flux coordinate system(x,y,z)[23]derived from an orthogonal toroidal coordinate system(ψ,θ,ζ).ψis the poloidal flux,θis the poloidal angle andζis the toroidal angle.The relation between coordinate system(x,y,z)and(ψ,θ,ζ)is in equation(11).νis the local field-line pitch given byν(ψ,θ)=B·∇ζ/B·∇θ=Bζ hθ/Bθ R,andhθ=1/∣ ∇θ∣is the scale factor forθ.The grid-point space size of the simulation region is(Nx,Ny,Nz)=(516,64,64).

A circular cross-section is adopted in this simulation.Major radiusR0=3.50 m,minor radiusa=1.19 m.The magnetic field at the magnetic axisB0=1.94 T.Figure 2(a)is the initial pressure and q profile,and(b)is the initial parallel current density profile.

3.Simulation results and analysis

Firstly,the linear phase of the P-B modes is simulated.The toroidal and poloidal modes of RMPs aren=3,m=5,6,7.Theamplitude modulationfactorof RMPisH=2.0×10−4,which represents a magneticperturbation about2.0×10−5−3.4×10−5T inψ=0.7−0.9.Since our simulation region in the radial direction isψnor=0.4−1.2,the region of RMP is alsoψnor=0.4−1.2.It is worth noting that a small vorticity perturbation is given as the initial perturbation in our simulation.The P-B modes(pressure perturbation)grow in the pedestal region because the driving source of the P-B modes is located here.Finally,we evaluated the convergent growth rate of pressure perturbation,which is the linear growth rate of the P-B modes.Figure 3 is the growth rates versus toroidal mode numbers(n)before the ELM crash.It is shown that RMP has no effect on the linear growth rate of the P-B modes.In our simulation,the amplitude of the RMP is incredibly small,and the RMP is added into equations as a magnetic perturbation.In the linear stage,the magnetic perturbation grows so rapidly that it is far larger than the RMP’s intensity in a short time.So RMP has a trivial influence on the linear growth rate of the P-B modes in the present simulation.In addition,this linear result is different from the result of Bécoulet et al[15].In fact,RMP can produce a variety of plasma responses(such as,shielding effect,resonant field amplification,etc),which can significantly influence the plasma flow,current,magnetic topology,turbulent transport and internal modes compared to that produced by the vacuum field alone.These effects may have an influence on the growth of modes.In our simulation,the response is not included in the model.However,Bécoulet et al take the response into account.Therefore,our linear result is distinct from the result of Bécoulet et al.

Secondly,the energy loss due to pedestal crash and turbulent transport in the nonlinear evolution of the P-B modes with/without RMP is also studied.In order to simulate it more efficiently,only 1/3 of the torus is calculated in the nonlinear simulation.ELM size[25]is just used for characterizing the pedestal energy loss in this work.In experiments,most of the loss energy will arrive at the divertor along the scrape-off layer.Therefore,the pedestal energy loss is closely related to the transient heat load on the divertor,but this process is not taken into account because our research focuses on the effects of RMPs on the pedestal dynamics and the P-B modes.It may be included in our next work.ELM size is defined in equation(12)[25],which is the ratio of pedestal energy lossΔWped(t)to pedestal stored energyWped.P0is the equilibrium pressure.ψin=0.4is the inner boundary of the simulation region.ψoutis the position of the largest pressure gradient.J is the Jacobian matrix.m/n=5/3,6/3,7/3RMPs are used.The amplitude

Figure 4.(a)Evolution of ELM size without and with RMPs(m/n=5/3,6/3,7/3 ).(b)Evolution of ELM size without and with RMPs(m/n=9/5,10/5,11/5 ).

In order to change the locations of the resonant surfaces,modulation factor of the RMP isH=1.0×10−4,which represents a magnetic perturbation about1.0×10−5−1.7×10−5T inψ=0.7−0.9.As shown in figure 2(a),the resonant surface positions are at the top,middle and bottom of the pedestal,respectively.Figure 4 shows the evolution of ELM size with and without RMPs.The Lundquist number,S=1×107(the typical value of Lundquist number is aroundS=106−1010in tokamaks[26])andαH=2×10−4is a little larger for the convenience of numerical calculation in figure 4(a).The blue dashed line is without RMP,the red,blue,and black solid lines are withm/n=5/3,m/n=6/3,m/n=7/3RMPs,respectively.It is found that the evolution process of ELM crash(shown in the following figure 4(a))includes several stages,which are the linear phase(t=(0−55)τA),the pedestal initial collapse(t=(55−80)τA)and the turbulence stage(aftert≈80τA).The resonant surface locations change with poloidal mode numbers,which leads to different mitigation effects on the ELM size.The pedestal does not collapse untilt=55τAin the linear phase.ELM size starts to increase and energy is released out from the pedestal radially aftert=55τA.The initial collapse of the pedestal is triggered when the most unstable mode with the largest growth rate grows to some extent in this simulation.Since the amplitude of the RMP is too small to impact the linear growth rate of the P-B modes shown in figure 3,the initial collapse intensity is the same regardless of whether there is RMP or not.At the turbulent transport stage,ELM size is reduced bym/n=5/3,m/n=6/3,andm/n=7/3RMPs,and the ELM size is the smallest with them/n=7/3RMP.The mitigation effects ofm/n=7/3RMP(corresponding resonant surface is near the bottom of the pedestal)andm/n=5/3RMP(corresponding resonant surface is near the top of the pedestal)are better than that ofm/n=6/3RMP(corresponding resonant surface located at the middle of the pedestal).In order to further investigate the mitigation effect of RMP with different resonant positions,RMPs withn=5,m=9,10,11 are used to affect the P-B modes and the pedestal energy loss,withS=1×108andαH=3.0×10−4.The results are presented in figure 4(b),which shows that ELM size is also reduced bym/n=9/5,10/5,11/5RMPs.The results in figure 4(b)could help us draw a clear conclusion that the reducing effect of RMPs on energy loss from the pedestal is obviously better when the resonant surface position is at the bottom and top of the pedestal,rather than in the middle,which is consistent with the results in figure 4(a).

The nonlinear evolution of ELM size consists of the initial pedestal collapse and the following transport process.In this stage,the P-B modes come into the nonlinear phase,and a variety of modes grow,leading to turbulent transport,and energy loss is mainly due to the turbulent transport.The turbulent transport is related to the fluctuation level and the propagation of the P-B modes.The case in figure 4(a)is analysed to get more details about the effects of RMP on the P-B modes and ELM size.The increase of ELM size results from the energy transported outward radially when the pedestal collapses.The P-B modes in the linear phase and the initial collapse process are shown in figure 5.The turbulent transport process is shown in figure 6.Figures 5(a)-(f)represent the pressure perturbations in the frame of normalized poloidal flux and toroidal angle without and withm/n=5/3RMP,respectively,and this is one-third of the torus.The pressure perturbation is normalized with the maximum at each time slice.In the linear phase(duringt=(0 -5 5)τA),as shown in figures 5(a)and(d),the initial mode(n=18),which is the most unstable mode with the largest growth rate,increases first accompanied by positive and negative perturbations appearing near the pedestal.Then,the negative perturbations begin to move inward and the positive perturbations move outward radially in figures 5(b)and(d),leading to pedestal collapse and the ELM size beginning to increase.In figures 5(c)and(f),negative perturbations spread further inward and the pedestal collapses acutely.The initial pedestal collapse is triggered when the most unstable mode grows large enough,and the collapse intensity is related to the strength of modes in the linear phase.The RMP is too small to influence the linear growth rate,thus the RMP has no impact on the pedestal crash in the early stage in this simulation.Therefore,the RMP has no evident effect on the development of pressure perturbation duringt=(0−80)τA.Figure 6 represents the pressure perturbation propagation in the turbulent transport stage(after aboutt=180τA).It is a nonlinear multimode developing stage,in which energy is lost from the pedestal due to turbulent transport,and the transport process depends on the fluctuation level and the propagation depth of negative perturbation.The results in figure 6 show that negative pressure perturbations propagate inward deeper without RMP compared to the case when RMP is added.It is found that the dominant mode numbers are n=12 both att=180τAandt=240τAwithout RMPs,as shown in figures 6(a)and(b).However,there is no single fixed dominant mode duringt=(180−240)τAwhen the RMP is added,shown in figures 6(c)and(d).From the above,a deeper propagation may happen when a single mode is dominated in the turbulence stage.

Figure 5.The pressure perturbation of the P-B modes in the frame of normalized poloidal fluxψ and toroidal angleζ at various moments.(a)-(c)are without RMP;(d)-(f)are withm/n=5/3 RMP respectively.

In order to obtain a clearer conclusion about the restraining effect of RMPs with different resonant surface locations on the radial spread of negative pressure perturbation,all of the cases in figure 4(a)are further analysed.Here,we show the evolution of pressure perturbation RMS(rootmean-square)of the P-B modes at the outer midplane in figure 7.The pressure perturbation is normalized with the maximum at each time slice.It is found that the negative pressure perturbation spreads inward toψ=0.45(marked with a bold red line)radially duringt=(180−250)τAwithout RMP in figure 7(a),while in figure 7(b),the perturbation spreads toψ=0.57 merely when RMP(m/n=5/3)is added,indicating thatm/n=5/3RMP could restrain the pressure perturbation spreading inward evidently in the early turbulence stage(t=(180−250)τA).In addition,when the RMPs have mode numbersm/n=6/3and7/3,the pressure perturbation spreads toψ=0.52 andψ=0.47,respectively,which seems to have a weaker restraining effect on negative pressure perturbation propagation compared tom/n=5/3 RMP.It can be concluded that RMPs could restrain the radial inward propagation of negative pressure perturbation in the early turbulence transport process and the restraining effect decreases with the locations of resonant surfaces.

It is widely known that the development of turbulence can be suppressed by self-generatedE×Bshearing[27,28],and theE×Bshearing rate is defined as follows[27,28]:

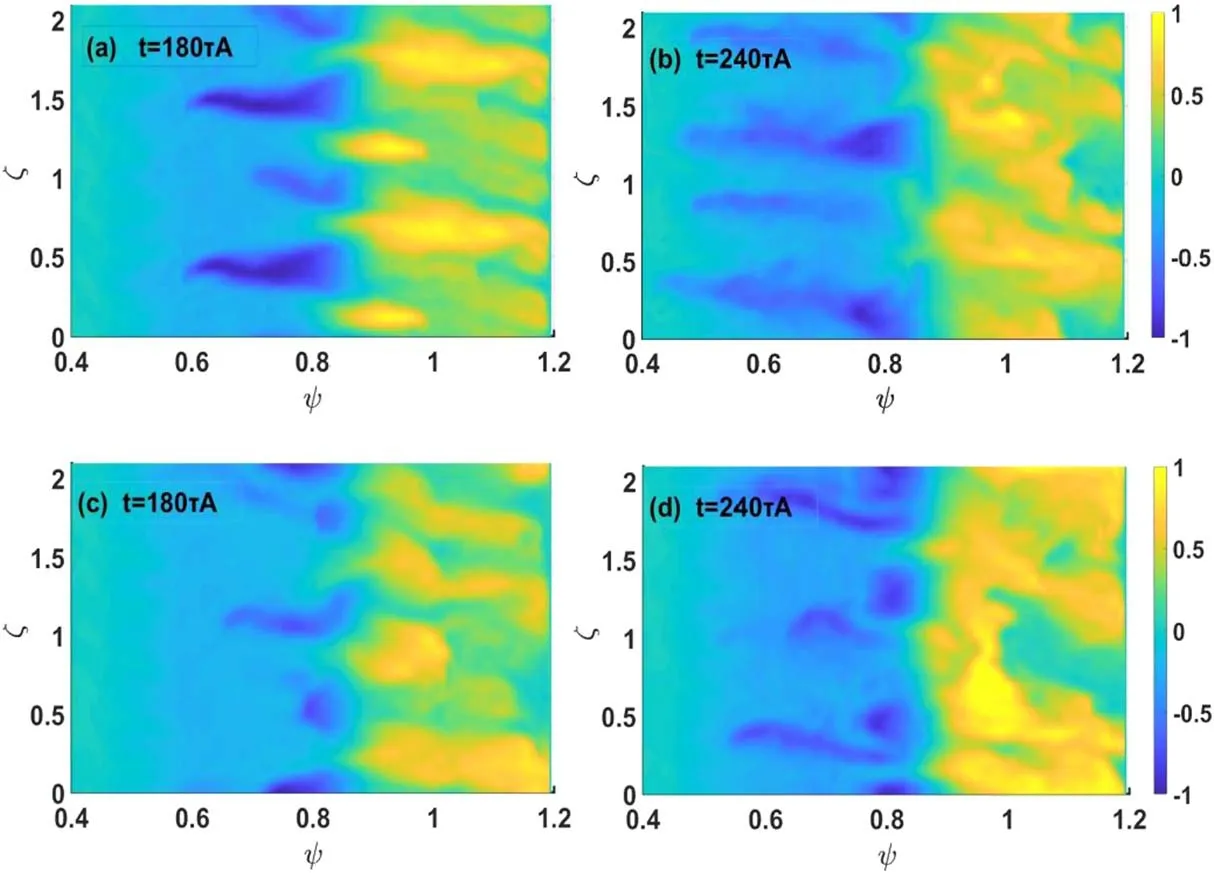
Figure 6.The pressure perturbation in the frame of normalized poloidal fluxψ and toroidal angleζ in the stage of turbulence phase.(a),(b)Without RMP;(c),(d)withm/n=5/3RMP.

Figure 7.Evolution of pressure perturbation in the outer midplane(a)without RMP,(b)with RMP(m/n=5/3),(c)RMP(m/n=6/3)and(d)RMP(m/n=7/3).The red bold lines mark the innermost positions of pressure perturbation spread radially.The black dashed lines in(b)-(d)show the positions of different resonant surfaces(m/n=5/3,m/n=6/3,m/n=7/3),respectively.

To have a vivid physical image of the restraining effect of RMPs on propagation of the negative perturbation of the P-B modes,the averageE×Bshearing rate〈ω〉tduringt=(180−250)τAis analysed.The averageE×Bshearing rate〈ω〉tis defined as:

The average of theE×Bshearing rate at the outer midplane duringt=(180−250)τAis displayed in figure 8.The results show that theE×Bshearing rate is stronger in the pedestal region,and it issignificantly stronger when RMPs are added,especially them/n=5/3RMP(shown in figure 8(b)),which is able to suppress the turbulence propagation and reduce energy loss from the pedestal duringt=(180−250)τA.However,theE×Bshearing rate withm/n=7/3RMP is too weak,leading to negligible restraining effects on the radial spread depth of negative pressure perturbation of the P-B modes.

To further investigate the mechanism of ELM size mitigation.We represent the fluctuation of the toroidal mode of pressure perturbation in figure 9.In figure 9(a),there are only a few modes(n=0,6,12,18)growing quickly at the beginning of pedestal crash(t=(60−70)τA),and the other modes(n=3,9,15)begin to grow slowly aftert≈180τA.However,in figures 9(b)-(d),almost all modes(n=0−18)grow immediately at the beginning of the pedestal crash(t=(60−70)τA).It illustrates that RMP can motivate mode coupling[15],which can lead to earlier growth of these modes(n=3,9,15).What is more,the results also show that these RMPs have different effects on the development of fluctuation level in the late stage of the turbulence phase(aftert≈300τA).For example,compared with the results shown in figure 9(a),the turbulence fluctuation level grows less in the late stage of turbulence phase(aftert≈300τA)with them/n=7/3RMP in figure 9(d),which might help reduce pedestal energy loss,while the turbulence fluctuation level in them/n=6/3RMP case is much stronger in figure 9(c).

From the above,the evolution of the P-B modes,including the propagation of negative pressure perturbation and turbulence fluctuation level,could be influenced obviously when the m/n=7/3 and5/3RMPs were added.As shown in figure 10,because the resonant positions ofm/n=7/3and5/3RMPs are at the peak of the positive perturbation and in the trough of the negative perturbation of the P-B modes,respectively,the RMPs may have a more obvious effect on the P-B modes in the turbulence phase.Them/n=6/3RMP may have a relatively weaker effect on the P-B modes since the resonant surface position(q=6/3)is in the nodal point of perturbation.Thus,compared with them/n=6/3RMP,them/n=7/3and5/3RMPs have stronger impacts on the P-B modes in the turbulence stage.

Figure 9.Fluctuation of toroidal modes of pressure perturbation.(a)Without RMP,(b)-(d)withm/n=5/3,m/n=6/3,m/n=7/3RMPs,respectively.Black dashed lines show the evolution of ELM size.Toroidal modes that n ＞18 are not represented here as they are too small.

Here,we tried to propose a mechanism to explain the mitigation effects of RMP on pedestal energy loss in the turbulent transport stage by investigating the effects of RMPs on the P-B modes,and pedestal energy loss is characterized with ELM size in this simulation.ELM size depends on the radial spread depth of negative pressure perturbation of the PB modes and the fluctuation level in the turbulence process.RMP can reduce the energy loss from the pedestal through the two following effects.Firstly,theE×Bshearing rate in the early turbulence stage(duringt=(180−250)τA)can be changed whenm/n=5/3andm/n=6/3RMPs are added,which helps to restrict the radial inward propagation of the negative pressure perturbation of the P-B modes.The restraining effect is weaker as the resonant surface position is radially further outward.Secondly,RMPs can motivate mode couplings,and they lead to earlier growth of the low to intermediate-n multimode instead of a single fixed dominant mode in the nonlinear phase,which may help reduce pedestal energy loss.What is more,the results also show that the RMPs have different effects on the development of fluctuation level in the late stage of the turbulence phase(aftert≈300τA).The turbulence fluctuation level grows stronger in the late stage of the turbulence phase(aftert≈300τA)withm/n=6/3RMP,while them/n=7/3RMP case is much weaker.

In brief,compared with them/n=6/3RMP,them/n=5/3andm/n=7/3RMPs can significantly influence P-B modes.TheE×Bshearing rate,which could suppress the radial propagation of negative pressure perturbation in the turbulent transport process,is stronger when them/n=5/3is added and the turbulence fluctuation level grows stronger in the late stage of turbulence phase(aftert≈300τA)with them/n=7/3RMP.Therefore,the RMPs can mitigate energy loss from the pedestal better when the resonant surface is near the bottom and top of the pedestal.

Since RMP withm/n=7/3demonstrates better performance in reducing the energy loss from the pedestal,we also simulated the mitigation of ELM size with different RMP amplitudes by changingthe amplitude modulation factor in figure 11.H=1.0×10−4represents a magnetic perturbation about1.0×10−5−1.7×10−5T inψ=0.7−0.9.It is found that the mitigation effect gets stronger when the RMP amplitude is larger.

4.Conclusions and discussion

The nonlinear evolution of ELM crash is a complicated process,which includes the initial pedestal collapse and the following turbulent transport stage.The ELM crash is closely related to the evolution of vorticity,magnetic field,parallel velocity,pressure,etc.The initial collapse is triggered when the most unstable mode with the largest growth rate grows large enough,and turbulent transport is related to the fluctuation level and the radial propagation depth of negative pressure perturbation,which could be suppressed byE×Bshearing.In fact,ELM control is an even more complicated multi-scale problem associated with the coupling of more than one mode element.In this paper,the effects of RMPs with various poloidal modes,corresponding to different resonant surfaces,on the P-B modes are studied numerically with BOUT++code.

The results of the linear simulations show that RMP has a trivial effect on the linear growth rate of P-B modes in the present simulation,thus the RMP has no influence on the initial pedestal collapse(t=(50−80)τA)intensity.One reason is that the amplitude of the RMP is too small to affect the linear growth rate evidently because the magnetic perturbation grows far larger than RMP rapidly.

In the nonlinear phase,to investigate the RMP mitigation mechanism involved in pedestal energy loss with different resonant surface locations,various RMPs with different poloidal mode numbers(n=3,m=5,6,7 andn=5,m=9,10,11 RMPs)have been used to affect the P-B modes.The main conclusions are as follows.

(1)The reducing performance of RMP on pedestal energy loss is closely related to the position of the resonant surface.The RMPs have stronger reducing effects on pedestal energy loss when the resonant surfaces are at the bottom and top of the pedestal rather than in the middle.

(2)TheE×Bshearing rate is strong in the pedestal region,and it issignificantly stronger when them/n=5/3RMP is added,which can suppress the radial propagation of the negative pressure perturbation and reduce energy loss from pedestal.In addition,the restraining effect on the radial propagation is weaker as the resonant surface position is radially further outward.

Figure 11.Evolution of ELM size without and with different RMP amplitudes form/n=7/3.

(3)Although the externally applied field perturbation is small(about 10−5T),the influence of RMPs on the mode coupling and saturation is quite significant in the nonlinear stage.It is found that RMP can motivate mode coupling and some modes(n=3,9,15)increase earlier than the case without RMP,while there would not be a single fixed dominant mode in the nonlinear stage.Multi-mode coupling would help reduce ELM size,which is consist with Bécoulet et al’s work[15].Furthermore,the turbulence fluctuation level becomes lower in the late stage of the turbulence phase(aftert≈300τA)when them/n=7/3RMP is added,which might also help reduce pedestal energy loss.

In this work,ELM size is just used to define the pedestal energy loss,and a physical mechanism is proposed to explain the mitigation effects of RMP on energy loss.ELM size depends on the radial propagation depth of the negative perturbation pressure and the strength of the fluctuation level in the turbulent transport stage.The averageE×Bshearing rate is significantly stronger when the RMP(m/n=5/3)is added,which can suppress turbulent transport.Although the restricting effects on the radial inward spread of negative pressure perturbation are not obvious whenm/n=7/3RMP(resonant surface locates at the bottom of the pedestal)is added,the turbulence fluctuation level could be suppressed significantly.Thus,it has a better mitigating performance on pedestal energy loss.

Recent studies,including experimental evidence and modeling results[29],seem to suggest that the RMP penetration occurs at the timescale of several milliseconds,which is a relatively slower process compared with our simulation time(about 10−5s).Plasma may not have enough time to produce response effects and these response effects may not be obvious when RMP is just added.Therefore,as the first step of the study,we preliminarily investigated the effects of RMPs on the P-B modes and the pedestal without taking the plasma response into account,and the qualitative effects of RMPs on the P-B modes and the pedestal are preliminary reported in this paper.This work probably could not be applied to explain the mechanism of RMP ELM mitigation directly at present,but it might be applied to investigate the effects of RMPs on the P-B modes and the pedestal dynamic process.

In fact,RMP can produce a variety of plasma responses in several milliseconds,such as screening the external vacuum field at the rational surface and amplifying the external field,which can significantly change the magnetic topology compared to that produced by the vacuum field alone.It is widely known that RMP can produce a magnetic island at the resonant surface.The island formation due to RMP can be influenced by the shielding effect(such as,island width can be suppressed).The shielding effect may be so strong that the stochastic field region may not be able to form.In all,plasma response plays an important role in the actual RMP distribution,which can influence topology,plasma rotation,current,turbulent transport,kinetic plasma dynamic and so on.Therefore,there will be some influence of the plasma response(such as,shielding effect,RFA,etc)on the effect of RMPs on the P-B modes,and our conclusions may have some differences compared with the case where response is taken into account.The numerical simulation of the effect of RMPs on the P-B modes,including plasma response and self-consistently kinetic plasma dynamics,is under investigation,and we will deeply investigate the mechanism of the effects of RMPs on the P-B modes by comparing the difference between the effects of RMPs with and without a response in our next work.

Acknowledgments

The authors wish to thank X Q Xu and T Y Xia for their contributions to the BOUT++code and thank W P Guo and C Y Su for their help.This research was supported by National Natural Science Foundation of China(No.11775154)and the National Key R&D Program of China(Nos.2017YFE0301203,2017YFE0301101 and 2017YFE0300500).