SBS:基于固态盘内部并行性的R-树高效查询算法
2020-11-10陈玉标李建中李英姝
陈玉标 李建中 李英姝,2
1(哈尔滨工业大学计算机科学与技术学院 哈尔滨 150001)
2(佐治亚州立大学计算机科学与技术学院 美国佐治亚州亚特兰大 30303)(chenyubiao@hit.edu.cn)
闪存固态盘以其耗能低、体积小、高可靠性、读写速度快等特点,快速地取代机械硬盘,成为无论是个人电脑,还是数据中心的主流存储设备.与此同时,技术的进步和越来越多的硬件资源被集成进固态盘,使固态盘拥有丰富的内部并行性[1-4].近些年,学者们针对该特点,开始研究如何发挥固态盘的内部并行性.例如,一些人开始研究如何利用固态盘内部并行性加速数据库中一些基础操作和索引,如数据库表的扫描与聚集[5]、B+树[6]、R-树[7]、LSM-树[8]、文件系统[9]等.
R-树是Guttman[10]于1984年提出的用于空间数据管理的树索引结构,它在理论和实践中都取得广泛应用[11],例如在著名数据库Spatial Hadoop,MySQL,PostgreSQL和GIS软件平台ArcGIS中都支持R-树索引结构.在R-树的基础操作中,范围查询是最具有代表性的操作.实际上,对于地理数据,例如GML(geography markup language)文件而言,实际操作主要集中在范围查询上,因而范围查询的执行效率对于R-树的性能至关重要.
R-树的特点有:任意子树最小外接矩形之间允许重叠,因此即使对于精确匹配查询操作,其查找路径也不是唯一的,往往结点的多个子树都需要被查询.因此,对于范围查询,R-树索引结点的读操作往往比较密集.这为利用固态盘的并行性优化R-树索引提供了可能.
因而,本文主要研究如何利用固态盘内部并行性去加速R-树的范围查询.目前,针对R-树上范围查询的优化工作,主要关注在内存环境下多核和多线程并行发挥和外存环境下机械硬盘的IO减少.新型存储闪存固态盘的出现,为我们提供了新的存储特性,除了快速随机读写外,另外还包括固态盘的内部并行性.该特点之前并未被考虑,本文就着重从充分发挥固态盘内部并行性的角度去优化R-树的范围查询操作.
本文的主要贡献包括3个方面:
1) 提出基于栈结构的范围查询算法SBS,该算法能充分发挥固态盘的内部并行性;
2) 从理论上证明SBS的内存使用上界;
3) 针对千万级别的数据,对本文提出R-树的范围查询算法SBS和另外3种算法进行对比实验,验证SBS算法的性能.
1 相关工作
地理信息系统在社会生产和生活中起到非常重要的作用,而该类系统的主要操作为范围查询,R-树作为其存储数据GML文件上的索引结构,其范围查询的性能对于整体系统的性能至关重要.因此对于R-树范围查询的优化具有重要意义.接下来,我们概述R-树范围查询优化的研究工作.
第1类工作:通过缩小MBR(minimal bounding rectangle)加速范围查询.在R-树的范围查询过程中,MBR对于判定是否可能存在查询结果起到至关重要的作用.MBR越大,重叠机率越大,查询过程中加载索引数据就越多,查询性能越低.因此,想方设法让MBR面积更小,就能够提升R-树的查询性能.文献[12]针对轨迹数据,把轨迹数据分段计算出一种更紧凑的MBR以提升查询效率.上述算法针对的是特定结构数据,而文献[13]基于bitmap位图索引构造出一种通用的缩小MBR的方法.它把MBR化成8×8的位图,如果对应区域有数据就置为1,否则置为0,这样就能更细粒度地表达一个数据对象或者子树的外形,从而能够尽可能地去减少MBR重叠误判率.这些缩小MBR的思路都是让MBR形状更接近真实数据的分布,还有另外一种思路就是让数据放得更紧凑一些,以此来缩小MBR.文献[14]基于希尔伯特曲线将近似的数据尽可能放到一起,这在减少MBR的同时,也可以降低机械硬盘的访道距离以提升整体的查询效率.
第2类工作:通过并行执行来加速范围查询.在外存机械硬盘环境中,文献[15]针对单CPU多磁盘的存储模型设计出索引的存储策略,当有新的索引结点被创建时,根据算法策略判定该结点的不同磁盘存放位置,使R-树索引上的范围查询可以发挥磁盘的并行性.由于大内存环境的出现,在内存环境中,关于R-树的研究工作也开始出现,随着技术的进步,服务器中集成了越来越多的处理器和核,于是文献[16]开始考虑利用多核多线程的并行来加速R-树索引,其中包括范围查询.另外,GPU的计算能力近些年以惊人的速度增长,文献[17-19]开始考虑使用GPU加速R-树索引以及R-树上的范围查询.
第3类工作:根据存储介质特点来加速范围查询.传统外存存储介质为机械硬盘,它的代价主要和寻道距离有关,因此机械硬盘对于随机访问操作非常不友好.而R-树的范围查询恰恰会产生大量的随机访问,文献[20]针对R-树的叶子结点访问,通过skip-sequential prefetch技术使得大量叶子结点的随机访问变成顺序访问,以此来减少范围查询代价.闪存介质作为一种新型存储介质拥有和磁盘完全不同的特性,首先是读写不对称,其次是擦除次数有限.因而,针对闪存介质的R-树优化主要集中在这2点上.近些年,关于R-树的优化主要考虑减少写操作来提升R-树的性能,而为了达到这个目的,额外的读操作是可以被牺牲来换取更少的写.宏观上来看,是牺牲R-树查询性能来换取更新操作的性能.其中,文献[21]通过缓存来减少更新;文献[22]用批量更新代替即时更新;而文献[23]把每个结点的更新操作信息存储到更新日志中,当结点被查询时,才会将更新操作作用到结点.这无一例外是减少了写的代价,但却增加了额外读的代价.
本文主要从存储介质特点的角度去考虑对R-树索引的范围查询进行优化.传统机械硬盘主要考虑查询过程中减少随机写或者是减少寻道距离.而针对闪存存储介质,基于该介质的读写不对称以及擦除次数有限的特点,优化目的更着重于减少写操作,也就是更偏向于优化更新操作.而闪存固态盘除了拥有闪存介质的特点外,作为一个整体来看,还拥有丰富的内部并行性.本文考虑如何利用固态盘内部并行性来加速R-树的范围查询.
2 背景介绍
2.1 固态盘的内部并行性
如图1所示,经典的闪存固态盘包含4个部分:主机接口逻辑模块、内存缓存模块、固态盘控制器模块、闪存包模块.多个闪存包通过共享的数据通道连接至闪存控制器.一个固态盘通常含有2~10个通道来传输数据.在通道数据传输中,控制指令执行时间相对于数据传输时间非常短,可以忽略不计,因此可以认为通道之间工作是独立的.同样也可以认为不同包之间的工作也独立.那么根据上述描述,在闪存固态盘内部,至少存在2个层级上的并行性:通道级别并行和闪存包级别并行.假设通道为m个,每个通道连接n个闪存包,理论上最大并行度为mn.为了利用上述并行性,需要批量地提交大量的IO请求到每个通道与之连接的每个闪存包来使得固态盘的并行性得到充分发挥.文献[7]实现一个并行批量提交算法ParallelIO,它的输入为IO请求集合,输出为加载结果集.文献[7]从理论和实验都证明它能够实现一个比较可观的加速效果.本文的优化算法均基于该算法实现.
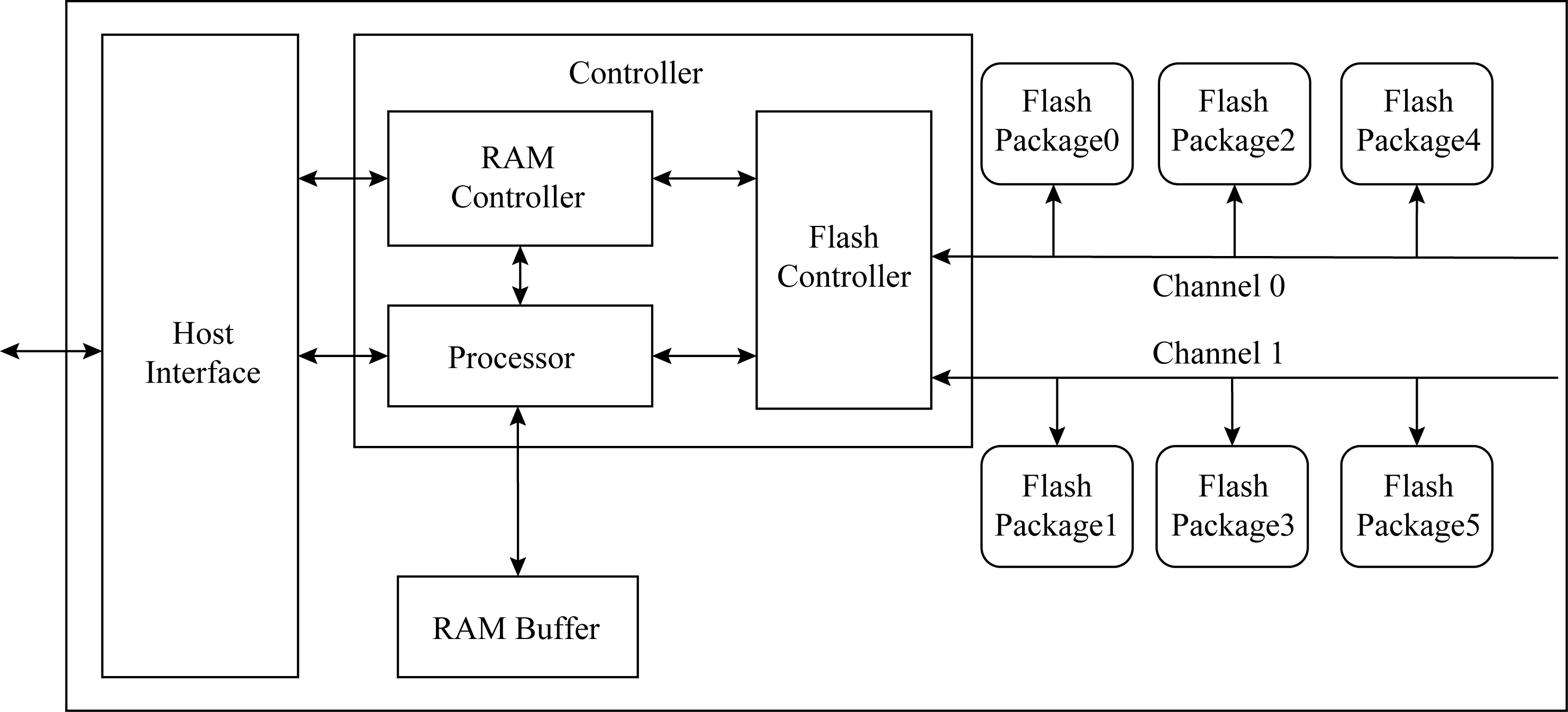
Fig. 1 The architecture of solid state drive
2.2 R-树表示和范围查询定义
本节给出R-树索引结构的描述和范围查询的定义.
R-树是目前最广泛使用的空间索引结构,它本质上是B-树在高纬的拓展,因此它的索引结构和B-树类似.对于一棵L阶、最大项数为M的R-树,它的索引结构可以描述为:
(Count,Level,Branch1,Branch2,…,BranchM).
1) 中间结点:Branchi=NPi,MBRi;
2) 叶子结点:Branchi=DPi,MBRi.
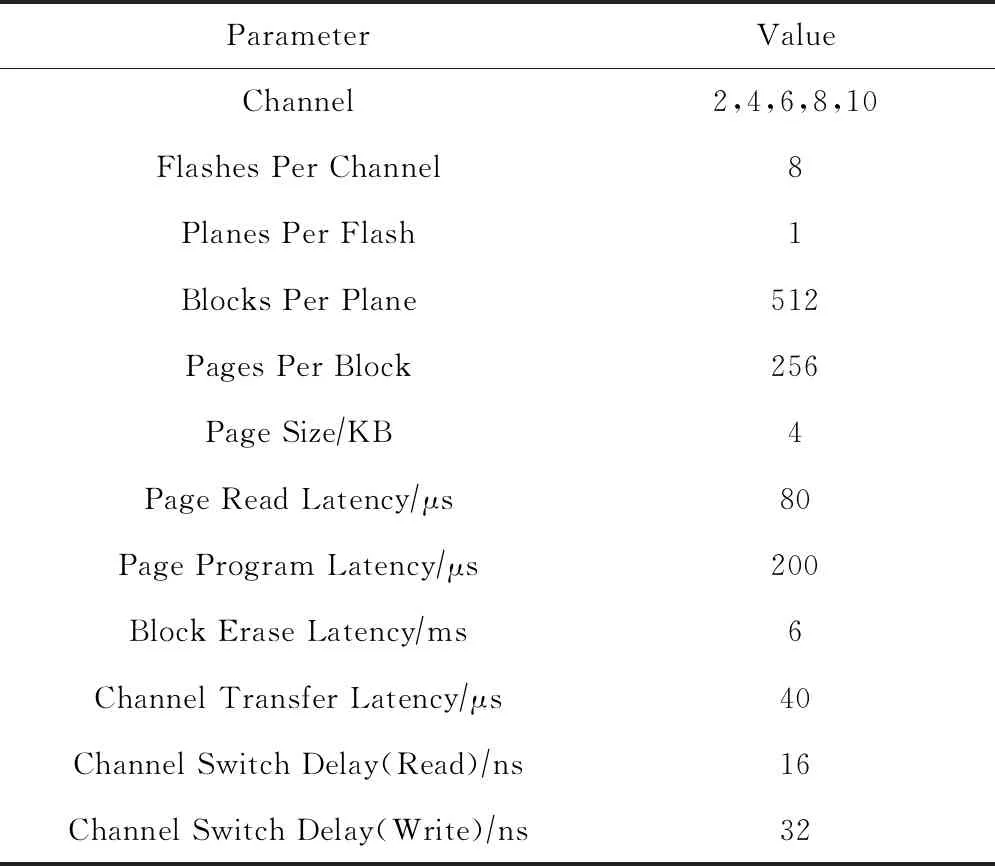
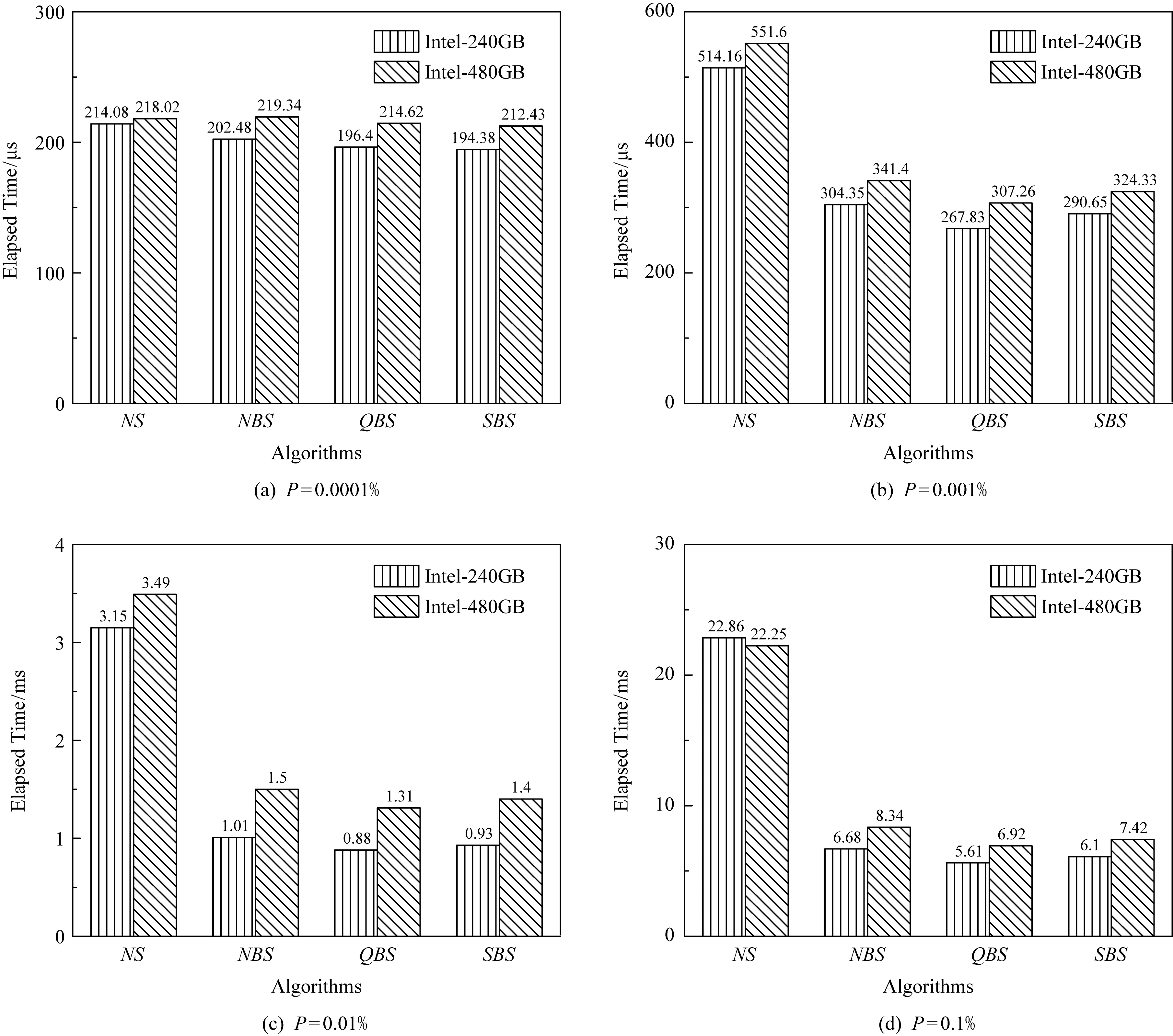
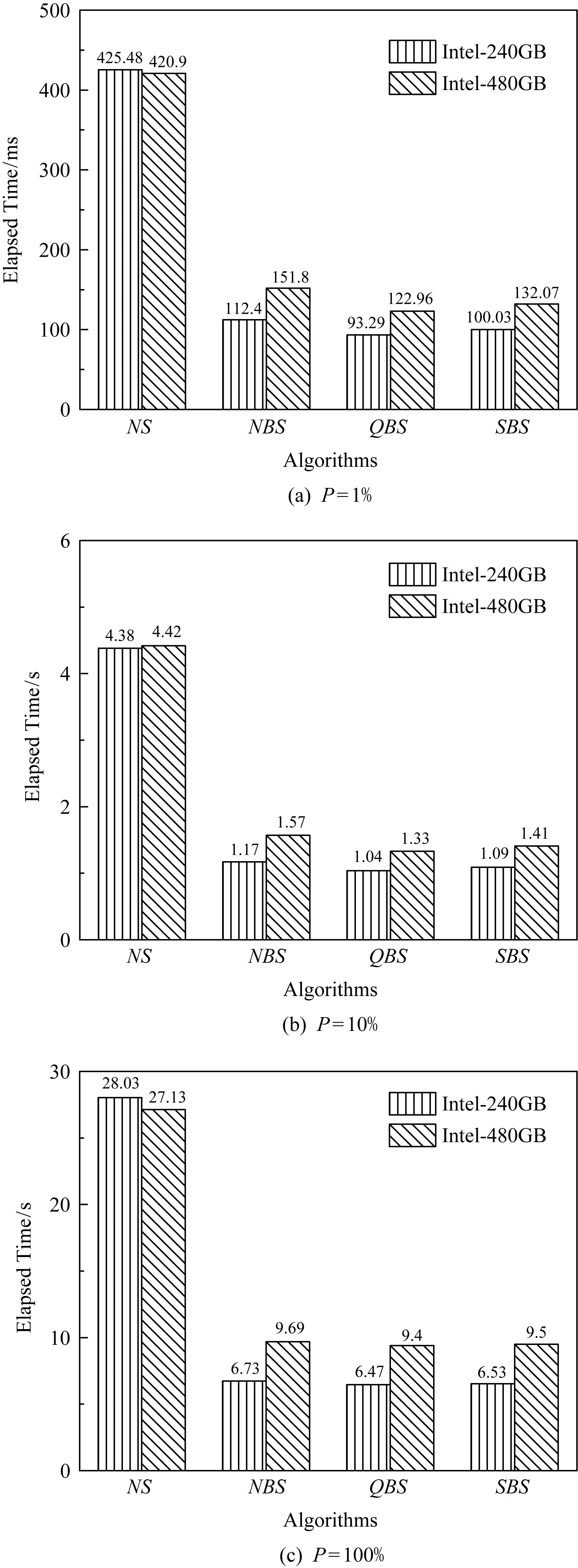
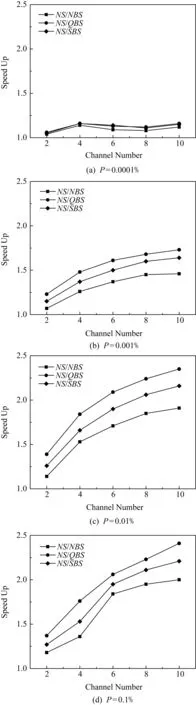
其中,Count∈[M2,M)表示结点中有效索引项或数据项数目,当L=0时,即当R-树根结点又是叶子结点时,允许Count 定义1.范围查询.对于外存R-树索引,输入根结点r,查询区域为m,要求从根结点r开始查询返回m范围内的所有数据索引集合S.这里S满足S={DPi|MBRi∩m≠∅}. 如图2就是一棵R-树和范围查询的例子,是一棵L=3和M=4的R-树.图2(a)为R-树的空间结构,图2(b)为R-树的索引结构.图2(a)中的虚线框m表示查询范围,图2(b)中每个结点上的通道号是R-树索引每个结点的存储单元连接在8通道固态盘上的通道号.查询结果就是落在虚线框中的黑色圆点的索引集合.这里假设图2中R-树索引每个结点单独占用固态盘1个物理页,固态盘读取1页的时间为T.本文提出的算法都将通过该R-树例子来具体说明. Fig. 2 An example of R-tree index range query 本节回顾R-树经典的范围查询算法NS(naïve search). 算法1.NS(r,m). 输入:r为R-树根结点,m为搜索的MBR; 输出:S为m范围内的数据索引集合. ①S←∅; ② if (r是非叶结点) then ③ for all (brancht∈r.branchs) do ④ if (t.MBR∩m≠∅) then ⑤child←read(t.NP); ⑥NS(child,m); ⑦ end if ⑧ end for ⑨ else ⑩ for all (brancht∈r.branchs) do 如算法1所示,输入为R-树根结点r,查询区域为m;输出为查找所有搜索矩形m覆盖的记录条目;算法返回查询数据的索引集合.算法1除去开头初始化和最后返回结果,主要共分成2个部分: S1. [查找子树](行②~⑧).如果r是非叶子结点,并且r所对应的矩形与m有重合,那么检查所有r中存储的条目,对于所有这些条目,使用NS操作递归作用在每一个条目所指向的子树的根结点上(即结点r的孩子结点). 下面以图2为例详细描述算法1的查询过程,并给出查询代价分析.查询过程从根结点A开始,首先枚举处理它的第1个儿子结点B,判断B是非叶子结点,那么进入S1子树查找模式;枚举处理B的第1个儿子结点E,判断E是叶子结点,进入S2叶子结点查找模式;判断E的儿子结点中落在m范围的有{P2},将其放入查询结果集合S中;E处理完后,继续枚举B的儿子结点F和G,它们均为叶子结点,将对应的查询结果{P5,P6}和{P7,P8,P9}放入S中.以B为根结点的子树被处理完后,继续以子树查找模式处理C,D.最终,将S的查询结果返回.默认根结点A已经加载至内存,整个过程需要依次加载的索引点为{B,E,F,G,C,H,I,J,D,K,L,M}.根据2.2节的假设读取一个索引结点的时间为T,那么整个查询过程IO时间为12T. 可以看出,算法1是简单的深度优先搜索过程,基于算法1的优化将在第3节并行优化算法部分给出. 在本节中,我们将设计用于R-树的范围查询的优化算法,首先给出一个直观的基准算法NBS(naïve batch search),它能够在不改变原来搜索策略的同时发挥固态盘的内部并行性;然后,我们给出一个优化算法QBS(queue batch search),它提供了一种新的搜索策略,这种搜索策略会尽可能将IO读请求聚集然后批量提交,来使固态盘内部并行性充分发挥,但是它存在一个问题,那就是内存开销会比较大;最终,为克服上述缺点,我们给出一个有内存上界保证的范围查询算法SBS,它能在充分发挥固态盘内部并行性的同时,又能限制内存的开销在一个可接受的范围内.需要注意的是输出结果在具体实现中会先将结果放到写缓存区中,待缓存区满再写到外存中去,因此,文中用于衡量内存最大消耗的空间复杂度将不会把输出结果的规模计入.相关的的符号解释如表1所示: Table 1 The Symbols to Describe Algorithms 在算法1中我们发现,当对每个子树做查找时,对同一父结点的儿子结点之间的查找操作是相互独立的,可以被并行加载.基于该原则,给出一个基于经典查询算法NS的并行优化算法.在经典深度优先范围查询算法的基础上,对于每个访问的中间结点r,找出所有子结点中和搜索范围m相交的子结点索引集合,通过批量提交算法ParallelIO加载至内存,然后分别递归地进行子树查找. 算法2.NBS(r,m). 输入:R-树根结点r、搜索的MBRm; 输出:S为m范围内的数据索引集合. ①S←∅; ②read_queue←∅;*用于批量读的队列* ③ if (r是非叶结点) then ④ for all (brancht∈r.branchs) do ⑤ if (t.MBR∩m≠∅) then ⑥read_queue.push(t.NP); ⑦ end if ⑧ end for ⑨children←ParallelIO(read_queue); ⑩ for all (nodechild∈children) do 算法2输入依然为R-树根结点r、查询区域m;输出为查找所有搜索矩形m覆盖的记录条目S;算法2主要共分成4个部分: S1. [初始化](行①~②).初始化用于存放查询结果的集合和用于批量提交的读队列均为空. 算法2基于深度优先,在递归调用最大深度为O(logN),因此递归中栈的最大空间为O(logN).而在每一层递归调用的过程中,需要聚集加载每层中所有和查询范围m相交的子结点索引并加载,该部分会产生O(B)空间的开销,那么最多产生O(BlogN)空间开销.因此算法2的空间复杂度为O(BlogN). 下面以图2为例详细描述算法2的查询过程,并给出查询代价分析.查询过程首先从根结点A开始,批量提交并行读取{B,C,D};依次对以B,C,D进行递归子树查找,依次分别批量提交读取{E,F,G},{H,I,J}和{K,L,M}.那么整个过程一共经历4次IO,由于通道之间传输完全并行,而每次加载的3个结点数据块分别连接在不同的通道上,因此每次批量提交读取结点的加载时间均为T,那么整个加载时间为4T.算法NBS相较于NS,在图2例子中加速比为3. NBS算法是在深度优先搜索过程中,对于每个中间结点r,找出所有子结点中和查询范围m相交的子结点索引集合,然后批量提交,以充分发挥固态盘内部并行性.如图2例子所示,这种方式并不能保证将批量提交的性能发挥到最大化,原因是每个被访问结点的子结点在查询范围内m的数量可多可少不能保证.实际上,对于被访问的r,除了让m范围内的子结点加载并行起来,还可以延迟等待其他结点,和其他结点的加载聚集起来一起批量提交.直观思想就是将所有的待加载结点都找出来聚集,以让每次批量提交加载的数量尽可能多,那么就能更大地发挥固态盘内部并行性. 基于上述优化思想,实现一个基于队列的广度优先的范围查询算法QBS,它维护一个已加载至内存结点队列node_queue和一个用以加载结点索引的队列request_queue.node_queue初始化为只包含根结点的队列,每次都将所有node_queue结点的子结点遍历将和m范围相交的结点索引添加至request_queue,其目的是尽可能让批量加载的并行性更充分.request_queue用于存放待加载索引集合,当所有可能产生结果结点的索引被找到后,便开始并行批量提交request_queue中的索引以加载待遍历的结点. 算法3.QBS(r,m). 输入:r为R-树根结点,m为搜索的MBR; 输出:S为m范围内的数据索引集合. ①node_queue←{r},request_queue←∅; ②S←∅; ③ while (node_queue≠∅‖request_queue≠∅) do ④ while (node_queue≠∅) do ⑤top←从node_queue中提取第i个结点; ⑥ for all (brancht∈top.branchs) do ⑦ if (t.MBR∩m≠∅) then ⑧ if (top为非叶结点) then ⑨request_queue.push(t.NP); ⑩ else 算法3输入依然为R-树根结点r,查询区域为m;输出为查找所有搜索矩形m覆盖的记录条目S;该算法主要共分成5个部分: S1. [初始化](行①~②).算法3维护3个队列:查询队列request_queue、结点队列node_queue和数据索引队列S,其中node_queue用于存放已经载入的内存结点,request_queue用于存放待载入内存结点的索引,S存放结果数据索引.该部分初始化查询队列和数据队列为空,初始化查询队列为输入根结点. 算法3采用基于队列的广度优先策略,最坏情况下,当每个被访问node_queue的队首结点为中间结点时,对于每个当前访问结点最坏会产生B个待加载结点索引.而只有访问结点是叶子结点时,处理完成后才是被彻底释放,不会增加新的待加载结点进request_queue,进而被加载放入node_queue.对于一棵平衡树,它的树结点索引规模为O(NB).因此,最坏的情况,所有和m相交的结点都堆积在队列中等待被处理,因此最坏的空间复杂度为O(NB). 下面以图2为例详细描述算法3的查询过程,并给出查询代价分析.这里默认NCQ_SIZE=32.按照算法3步骤S1,node_queue初始化只包含根结点A;按照步骤S3:取出node_queue的首结点A,枚举所有和m相交A的待加载儿子结点{B,C,D}的索引放进request_queue; 按照步骤S4:批量提交{B,C,D}的索引读取{B,C,D},然后依次放入node_queue.按照步骤S2,算法并未停止,继续运行.按照步骤S3,将node_queue中的所有结点{B,C,D}分别处理,获取待加载儿子结点{E,F,G},{H,I,J}和{K,L,M}的索引放进request_queue;按照步骤S4,批量提交加载{E,F,G,H,I,J,K,L,M},然后将已加载结点放入node_queue中;回到步骤S2,node_queue不为空,算法继续;按照算法步骤S3,遍历{E,F,G,H,I,J,K,L,M}获取数据索引放入S,此时node_queue和request_queue均为空;回到步骤S2,算法终止;步骤S5,返回查询结果S. 算法4基于栈来模拟递归调用的情形,不同于朴素用栈模拟递归调用问题的方法,在每次处理到任意结点时:如果该访问结点未被加载,由于一次批量提交可以加载NCQ_SIZE个结点.那么,我们往堆栈栈底方向寻找,尽可能聚集满NCQ_SIZE个子结点再并发提交以提高读性能.当堆栈中的结点不满NCQ_SIZE时,寻找先序遍历顺序的后续待加载的结点一起合并提交.如果该访问结点是已经加载时,直接处理其子树分支即可. 算法4.SBS(r,m). 输入:r为R-树根结点,m为搜索的MBR; 输出:S为m范围内的数据索引集合. ①node_stack←{r},S=∅; ② while (node_stack≠∅) do ③top=node_stack.top(); ④tmp_stack=∅; ⑤ if (top未被加载) then ⑥ while (node_stack中未加载的结点数≤NCQ_SIZE) do ⑦ if (node_stack=∅) then ⑧ break; ⑨ end if ⑩ 从node_stack中不断取出结点数据压入tmp_stack直到第1个已加载结点uncle; node_stack; node(t.NP)); 算法4共分为5个部分: S1. [初始化](行①).算法初始化.初始化返回的数据索引集合S=∅,初始化存放已加载内存结点的栈node_stack={r}. 算法4采用一个栈结构,栈每次遍历一层结点最多压入B+NCQ_SIZE=O(B)个元组,最多递归深度为该树索引的高度O(logN),最多压入元素个数为O(BlogN).因为,这里面栈占据了最大的内存使用空间,当栈内结点弹出,处理后即可释放.因此,算法4的空间复杂度为O(BlogN). 下面以图2为例详细描述算法4的查询过程,并给出查询代价分析.按照算法4步骤S1:堆栈node_stack只包含根结点A,由于A默认已经加载,那么直接运行至步骤S4:由于A的儿子结点的MBR均和查询范围m相交,因此将D,C,B分别压进堆栈node_stack;然后按照步骤S2判断,算法继续;按照步骤S3:此时top未被加载,那么从node_stack栈顶开始往下寻找未加载的结点索引聚集得到{B,C,D},并且node_stack不含有可以产生新的未加载索引的已加载结点,于是直接批量提交读取{B,C,D}.此时栈顶为已加载结点B,那么按照步骤S4:遍历B的所有儿子结点,查找MBR和m相交的子结点为G,F,E,按此次序依次压入node_stack;回到步骤S2:因为node_stack不为空,因此算法继续;由于node_stack栈顶元素为未加载的结点E,那么进入步骤S3:首先从node_stack栈顶开始往下寻找未加载的结点和E聚集批量提交.包括E在内,只寻得{E,F,G},少于NCQ_SIZE=32,那么需要获取更多待加载的结点.方法是从node_stack开始寻找已加载结点,如果是未加载结点先压入tmp_stack,直到找到第1个已加载结点C,将C和m相交的待加载的儿子结点H,I,J依次压入tmp_stack.此时待加载结点依然不够,继续寻找到D,那么将其和m相交的待加载结点K,L,M压入tmp_stack.最后,将tmp_stack元素均弹出,压入node_stack.这样整体遍历依然满足先序遍历的顺序,接下来对从node_stack栈顶开始聚集未被加载的结点{E,F,G,H,I,J,K,L,M}批量提交.然后进入步骤S4来处理这些已经加载的叶子结点获取m范围内的数据索引加入S;最终进入步骤S5:返回查询结果S. 图2例子比较理想,实际固态盘是个黑箱,内存索引结点数据分布并不可知,假设索引数据是均匀地连接在不同的通道上,那么这就是一个球箱子模型,根据文献[7]的证明可知,算法4依然可以提供一个很好的加速比.如批量提交32个IO请求,对于8通道的固态盘,期望加速比至少为2.93. 本节将对本文提出的优化算法进行实验测试.优化算法基于在加州大学伯克利分校Gutman[24]提供的开源内存R-树实现.本节基于真实数据集合生成的数据测试NS,NBS,QBS,SBS的性能. 1) 真实固态盘测试平台.实验的平台为Dell PowerEdge R730,配置为:2×6核Intel Xeon处理器,主频1.90 GHz;32 GB内存;系统盘为2 TB 7200rpm机械硬盘;操作系统CentOS7.1,内核版本为3.10.0,libaio库版本为0.3.109;实验对象为表2中2块固态盘.为了消除文件缓存给实验结果造成的影响,文件打开模式为O_DIRECT. Table 2 The Testing SSD Parameters 2) 仿真固态盘测试平台.浪潮天梭TS860,配置为8×16核Intel Xeon处理器,32 GB×96=3 072 GB DDR4内存,1.2TB×8=9.6TB SAS硬盘.操作系统CentOS7.1,内核版本为3.10.实验对象为用FEMU[25-26]模拟的5款固态盘,配置参数见表3.由于真实盘很难进行控制变量,该仿真盘主要用于测试通道数对于算法性能的影响. Table 3 The Emulated SSD Parameters 3) 数据集合.测试使用的真实数据集合为美国50州的路网数据,该数据来源于美国国家地理数据库[27],共计11 278 412条数据,每个元组包含经纬度坐标和一组字符串属性值.范围查询操作的实验数据均由其产生. 4) 实验测试.本测试针对文中4种范围查询算法进行性能对比实验.在4.2节中,对于4种范围查询算法,分别从不同固态盘、查询范围2个角度进行对比,测试它们对这4种查询算法的性能影响.为了表达方便,下面将SSDSC2BB480G6R简称为Intel-480GB,SSDSC2KW240H6X1简称为Intel-240GB. 本节测试4种范围查询算法的性能,测试内容包含:小范围查询范围变化对于范围查询时间和加速效果的影响;大范围查询范围变化对查询时间和加速效果的影响.这2组实验分别在表2中2款不同的固态盘上进行实验,以考察2款不同的固态盘对于范围查询时间和加速效果的影响. 先介绍索引构建的过程.首先,根据美国路网数据构建一棵R-树索引,将共计11 278 412条数据依次插入到初始为空的R-树索引中,我们就创建了一棵拥有完全数据的R-树索引,这里把所有路网数据插入生成的R-树索引称之为Rfull.本节查询实验中,所有的查询操作均作用于Rfull. 本节考虑查询范围变化和不同固态盘对于范围查询算法加速性能的影响.因此,本文透过7组不同查询范围的测试数据在2款固态盘上实验来对4种算法进行测试,以检验查询范围对于它们性能的影响.设P为查询范围占整个数据集合MBR的百分比,这里使用P作为衡量范围查询操作查询范围大小的参数.生成P∈[0.000 1%,100%]共7组范围查询操作集,其中每组查询操作1 000个.在生成查询操作数据集合的过程中,对于每组查询操作保证P不变,即确保查询面积恒定.对于任意一组单个查询操作生成方法是,在保证查询区域面积不变的情况下,查询范围在各个维度上的长度随机生成.这里把数据集合分成2组:P∈[0.000 1%,0.1%]和P∈[1%,100%].下面将对于这2组不同范围的查询操作集在表2所示2款不同固态盘上对Rfull进行测试实验.实验将统计每组查询操作的平均执行时间.这里考察查询范围变化较小情况下对查询算法效率的影响,这里P∈[0.000 1%,0.1%],与之对应的是另外一组查询范围变化较大情况下对查询算法效率的影响P∈[1%,100%]. 这里先进行小查询范围情况下查询性能对比实验,比较在查询范围较小的情况下本文提出的3种算法NBS,QBS,SBS和经典查询算法NS的效率比较.图3是在2款不同固态盘上的小范围查询实验,可以看出QBS比NS要快很多,SBS执行时间略高于QBS.如图3(a)所示,在查询范围很小时,如P=0.000 1%时,NS,QBS,NBS,SBS执行时间几乎无区别,这是因为非常小的查询范围查询结果为空,异或查询范围不会和多个子树MBR相交即查询路径单一,单一路径上的任意2个结点都是加载依赖的结点,它们之间无法进行并行加载,使得固态盘内部并行无法发挥.因此在图3(a)中,4种算法的平均执行时间几乎相等.图3(b)(c)(d)展示了随着查询范围的变化,NS和NBS,QBS,SBS查询时间的差距越来越大,同样地NBS和QBS,SBS的执行时间差距也越来越大. Fig. 3 Effect of small search range for searching algorithms on SSDs 接下来进行查询范围较大查询性能实验,比较在查询范围较大情况下本文提出的3种算法NBS,QBS,SBS和NS的执行时间比较.图4分别是在2款不同固态盘上的大范围查询对比实验,可以看出QBS比NS要低,且随着范围越来越大,执行时间差距就越大.SBS执行时间略高于QBS.如图4(c)所示,在查询范围最大时,即P=100%时,QBS,NBS,SBS执行时间几乎无区别,且和NS差距达到最大.这是因为查询范围非常大为全索引MBR时,它会和所有子树和叶子结点的MBR相交,因此QBS,NBS,SBS算法都能很好地充分利用固态盘的内部并行性,因此QBS和SBS的优化就不会产生额外的加速效果.因此在图4(c)中,3种算法分别的平均执行时间NBS,QBS,SBS几乎相当,而和经典查询算法NS执行时间差距最大.图4(a)(b)展示了随着查询范围的变化,NS和NBS,QBS,SBS查询时间的差距越来越大,同时NBS和QBS,SBS的执行时间差距却越来越小. Fig. 4 Effect of large search range for searching algorithms on SSDs Fig. 5 Speed up and peak memory usage of proposed searching algorithms on SSDs 图5显示了3种优化算法相对于NS的加速比随着P变化的趋势.如图5(a)(b)所示,当P比较小时,随着P的变大,NBS,QBS,SBS的加速效果越来越好,即加速比逐渐变大;当P比较大时,随着P的变大,NBS,QBS,SBS加速效果同样越来越好,而NBS,QBS,SBS之间的加速效果差距也越来越小.QBS虽然是执行效率最高的算法,但是根据算法空间复杂度分析可知,QBS空间复杂度非常高,如图5(c)所示,QBS随着P的逐渐增大,内存消耗越来越多,最大达到1.6 GB,而NBS和SBS内存消耗几乎可以忽略不计.因此,如果内存受限,SBS一定是最优选择.所以,大家可以根据具体的情况,选择合适的优化算法来提高查询效率. 最后在仿真固态盘上测试通道对于算法加速性能的影响,仿真配置如表3所示.我们分别对通道数为2,4,6,8,10这5个仿真固态盘进行实验测试,用来说明通道数对算法加速性能的影响.如图6和图7所示,图6是在小范围查询数据集下通道数对算法加速效果的影响,图7为大范围查询数据集下通道数对算法加速效果的影响.图6(a)中,随着通道数的提升,算法加速效果几乎没有变化,这是由于查询范围小,并发性很低,多通道发挥不出效果;如图6(b)(c)(d),随着通道数的增加,相对于NS,QBS,SBS加速比会逐渐上升,但是加速的提升速度减慢,这是因为IO并发性存在,但是依然比较小,因此随着通道数的提升加速效果会有所增加,但是提升速度会下降.如图7所示,在大范围查询下IO并发性是充足的,因此随着通道数的增加,加速比斜率变小的速度更缓慢些.结合图6和图7整体加速比可以看出,QBS和SBS在较大查询范围情况下,通道数的增加对于加速比的提升很明显,通道越多,加速效果越好. Fig. 6 Speed up affected by variant channel SSDs under small range search 地理信息系统在人们生产和生活中起到越来大的作用,作为该系统的核心索引R-树,主要接受的是范围查询操作,那么对R-树的范围查询算法效率改进对于整体系统的性能提升具有重要意义.由于闪存固态盘逐渐成为主流存储设备,它不同于传统机械硬盘存储,拥有很多自己的特点.于是本文从固态盘内部并行性这个特点出发,针对R-树的范围查询操作设计出一系列新的范围查询算法包括NBS,QBS,SBS来发挥固态盘内部并行性,以提升R-树索引范围查询效率.通过理论分析和实验证明:QBS最能发挥固态盘内部并行性,但是需要消耗大量内存;NBS算法实现容易,内存消耗最少,但是在查询范围较小情况,加速效果会减弱;为了更能发挥固态盘内部并行性,同时内存消耗又要很低,本文提出基于堆栈的范围查询算法SBS.通过理论分析和实验证明,它可以在消耗很少内存的情况下,高效地发挥固态盘的内部并行性. 在实验过程中会发现不同的闪存固态盘,在进行算法比较时加速效果会出现差异,这是由于不同固态盘内部并行资源的不同导致.因此在选购固态盘时,如果想充分发挥本文提出算法SBS的性能,应当选取内部并行资源更丰富的固态盘作为存储盘.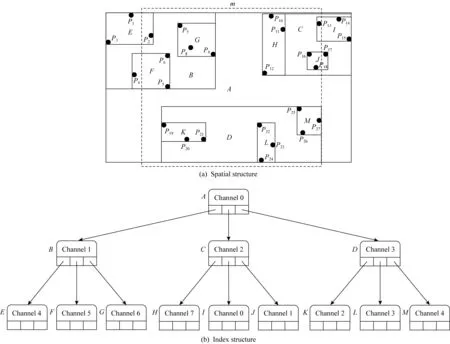
2.3 经典范围查询算法NS
3 并行优化算法

3.1 基准算法NBS
3.2 优化算法QBS
3.3 优化算法SBS
4 实验与结果
4.1 实验设置

4.2 查询实验

5 总结和未来工作
