飞翼无人机四维非线性反步制导律设计*

杨雷恒，岳 源，封承霖，王昭质，夏雁博

（1.西安航空职业技术学院通用航空学院，西安 710089；2.中国民用航空飞行学院航空工程学院，四川 广汉 618307；3.西安航空学院通用航空工程技术中心，西安 710077）

0 引言

随着各国防空力量的不断完善，对战机的突防能力也提出了更高的要求［1-2］。飞翼布局无人机取消了雷达发射面积最大的垂尾，再加上其天然具有的翼身融合体方式，为隐身隐蔽突防带来了极大的优势［3-4］。因此，飞翼无人机的作战能力越来越得到重视。

对于作战突防，可行的方案包括隐身突防和饱和打击两部分［5-6］。对于饱和攻击来说，要求打击系统几乎同时到达目标区域并实施打击。这种要求对制导系统来说就增加了对时间维度的控制需求。对于时间维度的精确制导方式，一般被称为四维制导方法。2019 年4 月，我国一架A320 四维航迹飞行管理能力试验飞机完成了天津至广州的往返航飞行试验，这也是亚太地区首次完成四维航迹精细化管制的试验飞行。同时，对时间维度的控制对无人机编队、快速机动目标跟踪、自主空中加油、巡航导弹拦截等任务至关重要。

飞翼布局无人机由于去掉了垂尾等气动安定面，使得其飞行和操纵存在更大的耦合和非线性特性［7-8］。特殊的气动布局，使得飞翼无人机在机动飞行时面临着非线性、迟滞效应、不确定扰动等因素的影响［9-10］。这些因素使得飞翼无人机精确航迹飞行控制存在困难［11-12］。

在航路跟踪设计的理论研究和工程应用中，常用的控制策略是对无人机速度和方向进行控制。但是，传统方法大多把无人机的运动被简化为质点，而忽略其非线性动力学特性。因此，本质上这些方法是基于简化模型开展设计的，并不适合非线性明显的机动飞行跟踪设计。

针对飞翼无人机的气动特性和四维航迹制导的需求，本文提出了一种利用反步控制方法的四维航迹制导律设计方法。该方法不仅有效地解决了飞翼无人机非线性问题，而且通过对速度的控制实现了对时间维度的控制。

1 控制/制导系统结构

在考虑无人机非线性特性时，无人机的航路跟踪控制器有以下两种系统结构［13］：一种为控制/制导一体化设计架构，另一种为控制回路和制导回路相对独立的系统架构。第1 种架构方式可以一次性完成系统的设计功能，但系统的稳定性、鲁棒性等指标很难得到充分考虑。第2 种方式系统层次分明、概念明确，便于针对不同层次的特点进行特定的设计，且具有方便工程实现的优点［14］。因此，第2种设计架构在工程和理论研究方面都受到了极大的重视。文献［15］采用了独立的系统架构，设计了基于视线法的航路跟随制导律。文献［16］在动态逆控制器的基础上，利用反步算法设计跟踪器。

控制回路的作用是保证系统的稳定性和鲁棒性，提高无人机的飞行响应性能。在控制系统设计方面，Backstepping 控制方法具有严谨数学表达和理论证明过程，具有解决非线性控制的能力。本文控制器采用了制导与控制回路相独立的设计思路，系统结构如图1 所示。根据该系统架构，可以根据对象的具体特性，有针对性的提高系统的性能。在制导回路设计上，本文将航路跟踪制导控制问题划分为虚拟向导飞行轨迹生成、非线性制导律计算和机动执行令生成3 个模块。其中，虚拟向导飞行轨迹生成模块主要功能是计算无人机沿参考航路飞行时的状态信息；非线性制导律计算模块的功能是计算无人机的制导指令；该制导指令经过机动指令生成器模块生成跟踪参考航路的力（力矩）和气流角等控制指令。

由于制导回路和控制回路相对独立，因此，需要通过制导/控制耦合回路把制导指令转化为控制回路的输入。

2 四维制导律设计

2.1 制导回律设计

基于反步法的航路跟踪制导律原理如下页图2所示。

图1 系统结构

图2 无人机航路跟踪

假设沿预定参考航路Γ 飞行的向导无人机p的运动方程可表示为：

无人机质心运动方程和动力学模型为：

下面推导非线性航路跟踪制导律。

定义航路跟踪误差：

对式（23）求导：

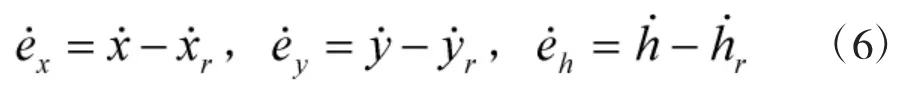
假如航路跟踪误差按指数收敛，则有：

由式（4）～式（7）可得：

对于上式的右端项，令：

由式（8）和式（9）可得：

令航路跟踪速度误差为：

对上式求导可得：

假设航路速度跟踪误差按指数收敛，则有：

由以上两式可得：

将式（3）带入式（17）经过整理可得如下航路跟踪制导律式：

下面应用Lyapunov 稳定性定理证明非线性航路跟踪制导律式（18）的收敛性。选取Lyapunov 函数如下所示：

将上式对时间求导可得：

非线性航路跟踪制导律的收敛性得证。

通过上面的推导和证明，可以得到如下定理：

2.2 虚拟向导轨迹的生成

从上节的航路制导律可知，为了实现无人机的航路精确跟踪，需要知道引导无人机在虚拟航路飞行时的状态信息。但是在工程上，参考航路信息一般为一系列关键位置处的坐标点。因此，需要研究基于坐标点获得向导无人机状态方程的方法。

图3 根据航点生成虚拟向导

同时，速度和加速度可根据任务需求和飞行性能综合给出。

2.3 机动指令生成

考虑到无人机采用倾斜转弯方式进行转弯，在转弯过程中侧滑角β 为零，侧力的影响这里不予考虑。式（23）的状态方程可表示为：

对上述3 式求逆可得：

3 耦合回路

制导/控制耦合器是连接制导回路和控制回路之间的通道，主要作用包括：控制信号不通坐标系间的转换和制导指令到控制指令的耦合生成。

3.1 不通坐标系下的角度转换

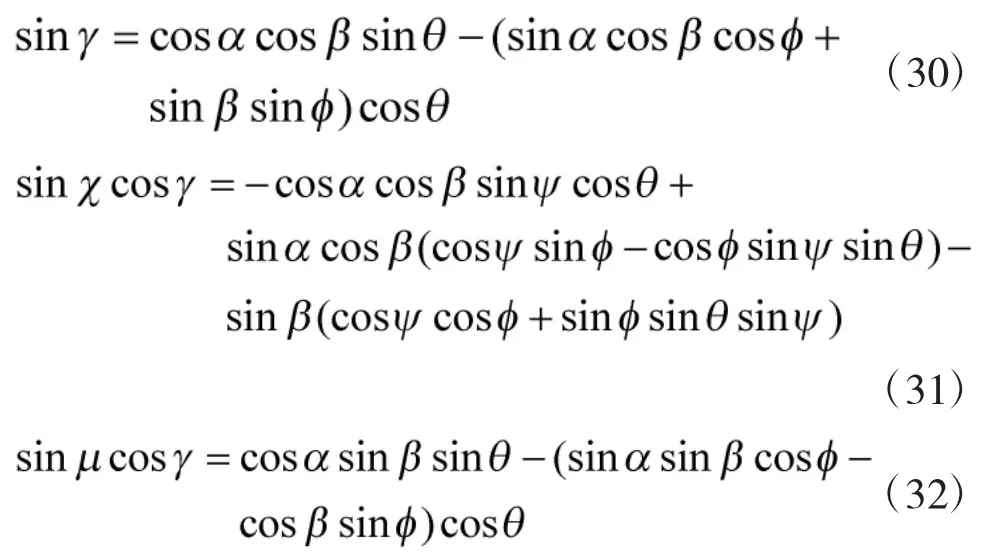
3.2 制导/控制耦合器

对于无人机的控制，总希望系统可以快速无误差的响应指令。为了消除静态误差这里构造了比例积分耦合器。耦合器的可表示为：

4 仿真验证

为了验证控制器的鲁棒性，在整个机动过程中选取如下气动系数发生不同程度的拉偏：其中，气动参数不确定的标称值如表1 所示，设定摄动参数为0.5。

表1 气动参数偏移幅度表

图4 无人机航路跟踪结果

在仿真结果中，红色曲线代表给点航点连接而成的航路，蓝色曲线表示无扰动情况下的跟踪结果，黑色曲线表示有扰动情况下的跟踪结果。下面给出长方形航路跟踪和蛇形航路跟踪仿真结果。蛇形航路的航点如表2 所示。

表2 参考航点

蛇形航路跟踪结果如下页图4 所示。

从仿真结果可知，无人机对于蛇形航路的跟踪航迹类似于一条正弦曲线。由于在同一峰谷间的两个航点距离较近，无人机需要较大的姿态调整转弯，更容易出现过调解的现象。蛇形航路的跟踪舵面响应去除掉控制部分输出后，制导带来的舵面相应如图5 所示。

图5 无人机出舵量

从各舵面响应来看：蛇形航路跟踪各舵面经过比较微小得到调节就实现了飞翼无人机姿态转换的跟踪控制。从以上仿真结果可以看出，本文提出控制/制导设计方法可以有效地跟踪无人机航路。

5 结论

针对飞翼无人机操纵能力不足、非线性和耦合性强等特点，以及对于航迹飞行过程中对时间维度控制的需求，本文提出一种四维非线性制导律设计方法。根据各功能模块独立设计的原则，文中的制导-控制系统包括制导回路、耦合回路和控制回路，并重点针对制导回路进行了设计。

在制导回路设计上，为了解决制导律设计对飞机飞行状态的依赖，文中引入了虚拟向导无人机提供制导律所需要位置和速度信息，并采用反步方法设计了四维航路非线性制导律。该制导律通过对飞翼无人机速度的控制，从而实现了对时间维度的控制。同时，为了连接控制回路和制导回路，文中设计耦合回路。文中采用六自由度模型对系统进行了仿真验证，证明该制导/控制设计方案是有效的。