多旋翼飞行器的三维时变编队量化控制
2020-11-10史浩宇
史浩宇
(空军工程大学航空机务士官学校航空仪电工程系,河南 信阳 464000)
0 引言
多旋翼飞行器在科研、民用、商业、军事等领域应用广泛[1],多旋翼飞行器的运动特性建模、控制、以及编队控制等问题也逐渐成为热点研究方向。由于多旋翼飞行器时变编队跟踪控制更具有工程意义和应用价值,因此,近年来得到了众多学者的广泛关注[2-4]。
多旋翼飞行器的建模十分重要。文献[5]建立了一个以速度、高度、航向角为控制指令的6 态模型,该模型的位置通道存在耦合,x 和y 通道的解耦依赖于确定的偏航角度。在文献[6]中,在编队控制率的设计中,将多旋翼飞行器偏航角设定为0,并只研究了在悬停或者小角度条件下的编队控制,在一定条件下实现了x 和y 通道的解耦,但是失去偏航和机动性的多旋翼编队在实际工程中应用较为困难。
编队系统需要通过相互传递信息来协同完成任务,而这些信息在被传递之前往往都需要经过量化。近年来,量化控制得到了大量的研究[7-10],文献[7]研究了一类随机非线性不确定系统的模糊自适应量化控制;文献[8]基于代数图论中的边拉普拉斯工具,研究了多智能体的量化自适应一致性;文献[9]提出了一种量化输入下的无人机时变编队跟踪控制方法;文献[10]针对具有不确定性和有限通信数据率的高阶非线性连续时间系统设计了一致性控制方法。尤其是随着网络化控制系统的应用和发展[11-13],又促使量化控制成为了解决网络化控制系统控制问题的一种有效方式。
量化控制的关键是平衡控制精度与低通信率的关系。关于输入量化的研究成果已有很多。目前,多无人机时变编队跟踪控制已取得了一系列成果,但考虑通信数据量化的研究成果较少。因此,飞行器的编队控制从理论推进到工程实践中,量化控制是一个值得研究的问题。
信号量化是指将信号从连续域映射到有限离散集的过程。在多旋翼飞行器编队中,飞行器通过通信模块相互发布状态信息,在数据传输过程中,存在一系列不可避免的问题,如:采样、丢包、传输延迟以及量化误差等。这些问题的存在会降低控制系统的性能,甚至导致系统的不稳定性,使系统的分析和设计变得更加复杂和具有挑战性。因此,量化控制的研究目标是希望经量化后的系统在通信速率尽可能小的情况下,仍能保持系统稳定并满足可接受的控制精度。
针对以上情况,并受文献[3,14]的启发,本文结合工程实际,搭建编队外环控制,将无人机位置信息、速度信息作为状态量,构建了一个二阶非线性模型,并针对该模型设计了编队量化控制器,设计了仿真实验,验证了所设计编队控制协议的有效性。
1 编队模型建立
1.1 多旋翼飞行器模型建立
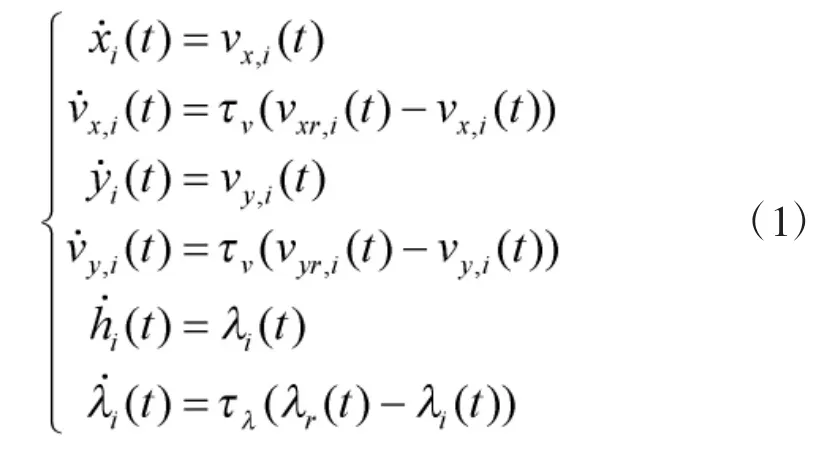
同时考虑多旋翼飞行器具有可悬停、欠驱动、电机升力有限的特性,存在以下实用性约束:
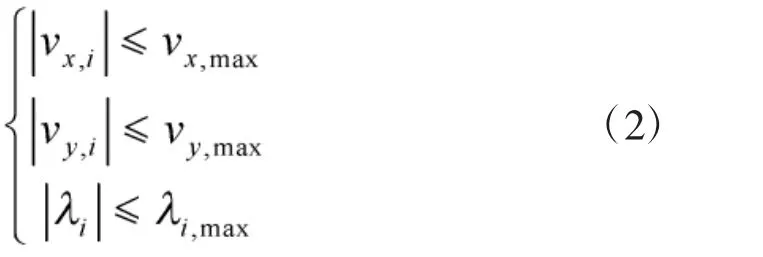
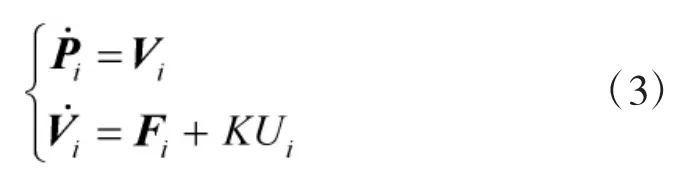
1.2 图论相关概念

在此基础上,引入图论工具入射关联矩阵E-、出射关联矩阵E+,定义如下

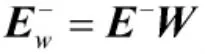


表1 本文中的图论符号
同时,针对生成边拉普拉斯矩阵存在以下引理。
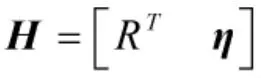
对矩阵Le进行相似H、H-1变换可以得到:
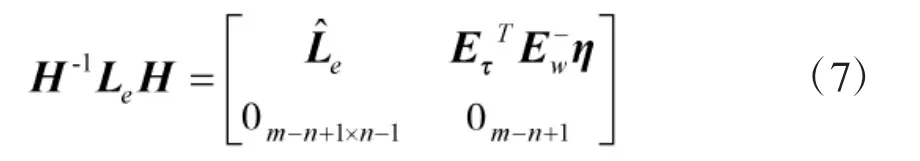
易得,如下方程的解即为分块矩阵的特征:
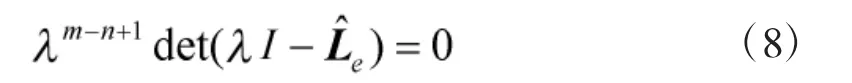
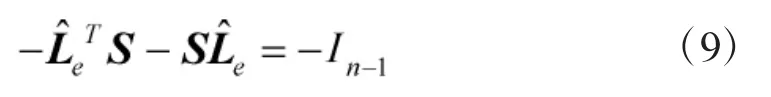
其中,S 为一个正定矩阵。
2 编队量化控制协议设计
多旋翼编队系统中的每架多旋翼飞机都能根据有向图传递信息。在控制协议的设计中,假设编队系统由n 架多旋翼构成,拓扑结构强连通。例如,图1 是由5 架多旋翼构成的编队系统,其拓扑结构是强连通的。
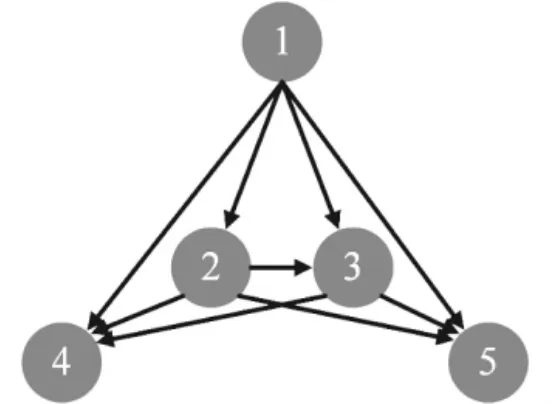
图1 由5 架多旋翼飞行器构成的有向图
本节要求设计控制率Ui使得多旋翼飞行器编队在量化通信情况下速度趋近一致以及每架多旋翼飞行器都可到达相对于编队中心的指定位置,即满足以下控制目标:
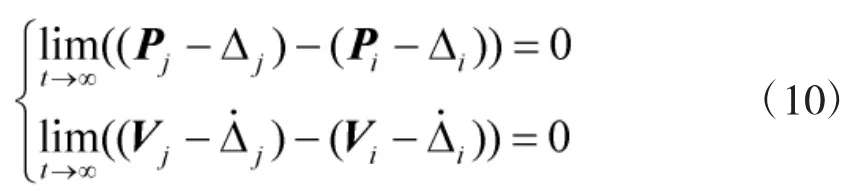
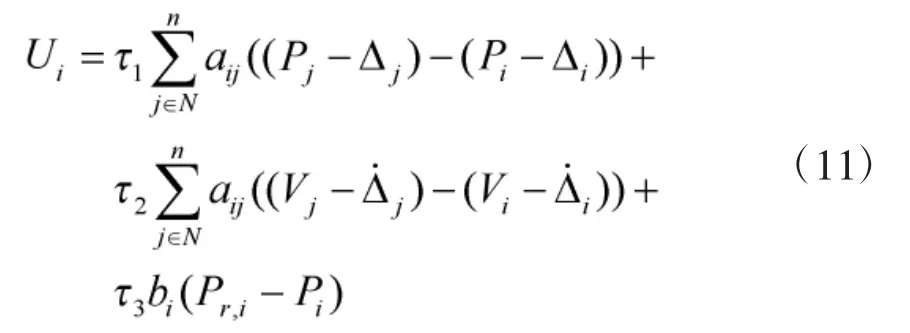
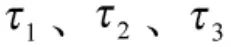
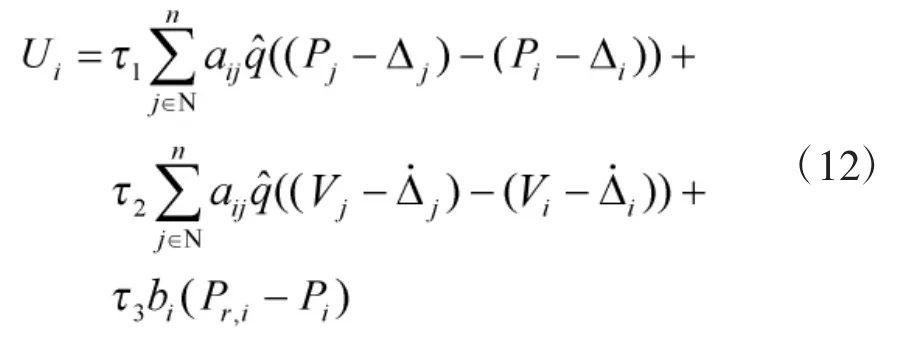
将Ui带入于式(3)表示的多旋翼飞行器数学模型,可改写为如下量化编队协议,
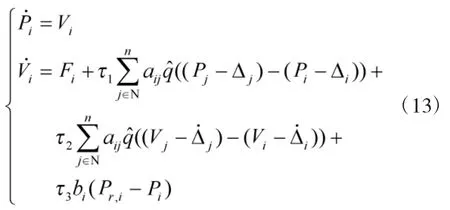
采用文献[18]中的技巧,来降低非线性问题的难度:
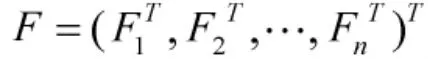
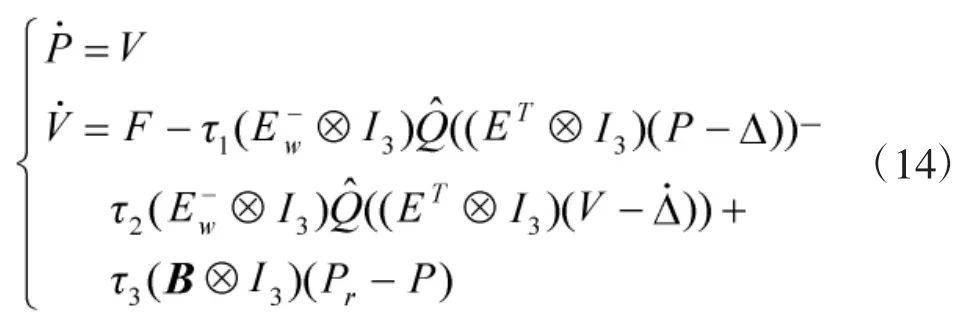
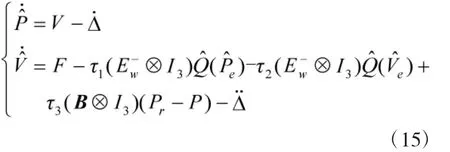
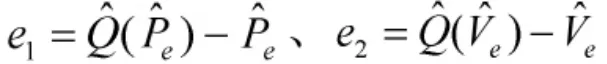
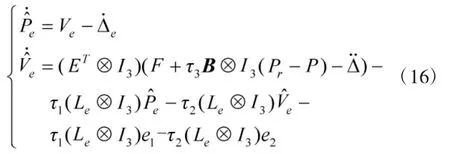
最终,控制目标式(10)可以调整为:

3 编队控制协议稳定性分析
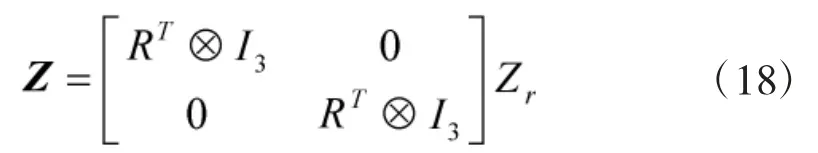
根据引理1 关于H 的定义,可以得到
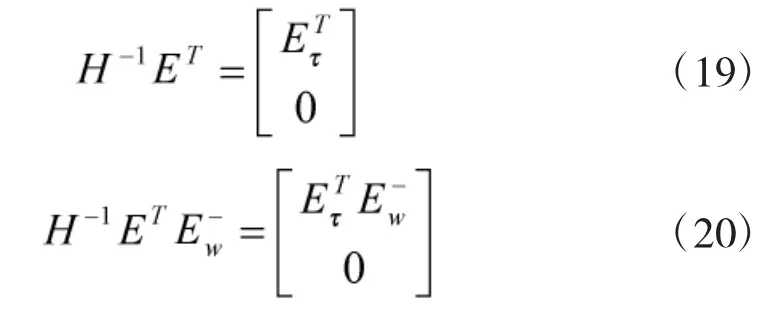
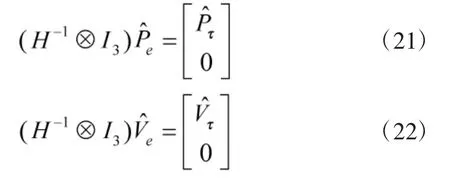
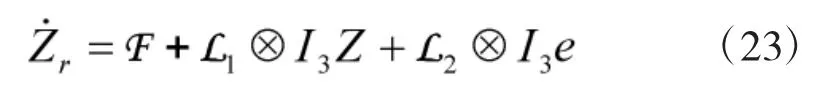
选取适当的李雅普诺夫函数:
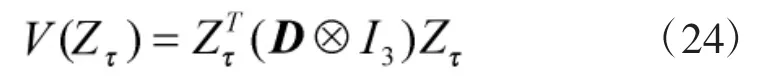
对其进行求导可得:
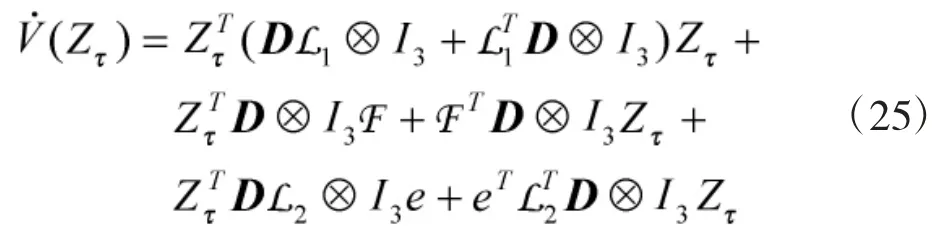
定义矩阵:
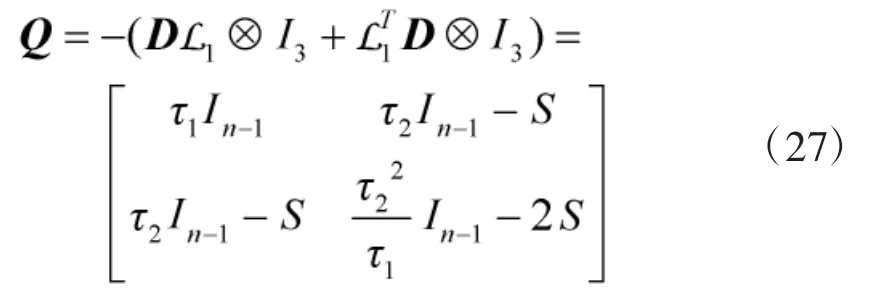
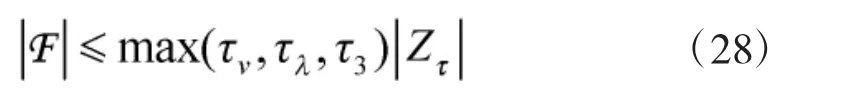

其中,m 为强连通图G 的边集的数量。
由于Q 矩阵正定,结合式(28)、式(29)可以得到:
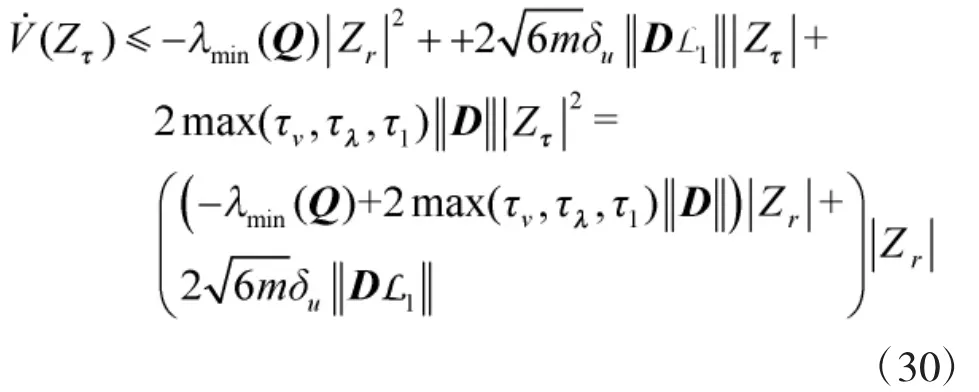
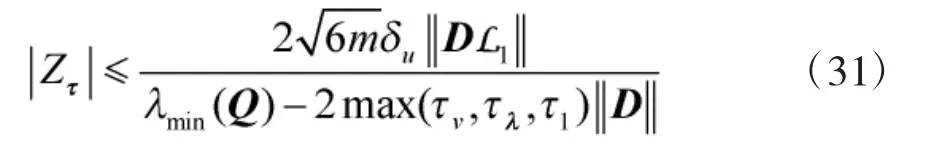
4 仿真与实验
为验证该编队控制率的有效性,设置仿真条件为:假设共有5 架多旋翼飞行器进行编队飞行,编队的拓扑结构如图1 所示,其参数设置如表2 所示。
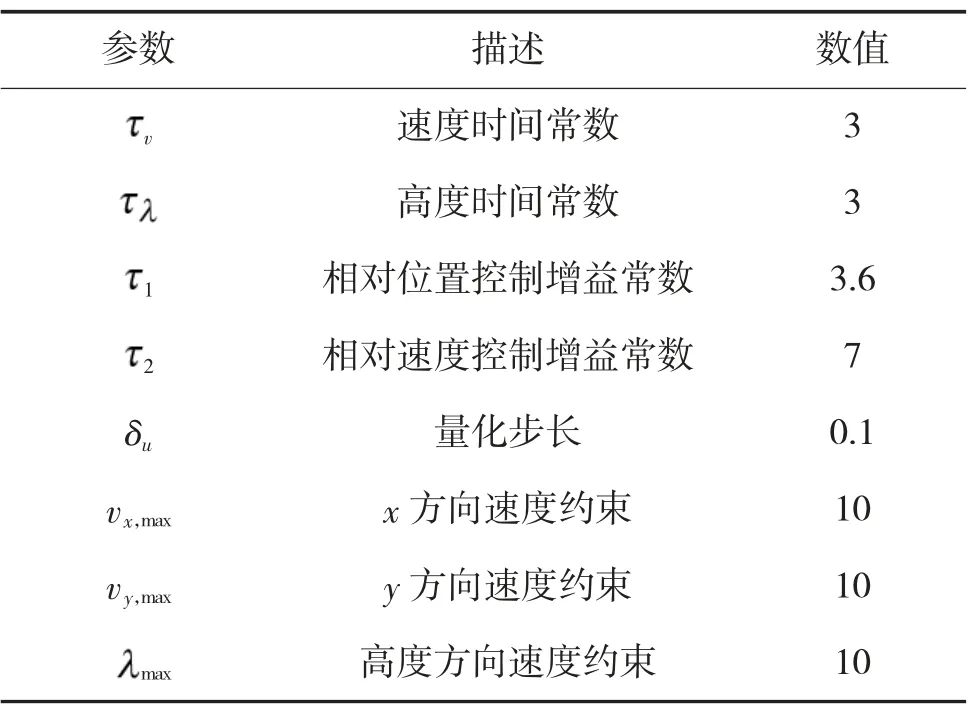
表2 无人机参数设置
期望路径设置为:
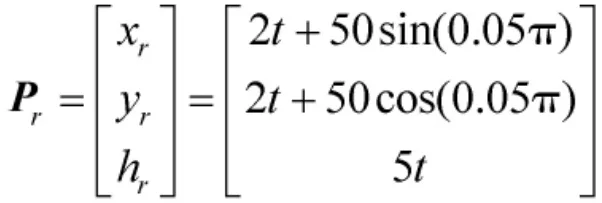
5架多旋翼飞行器的时变相对距离设置如表3所示。
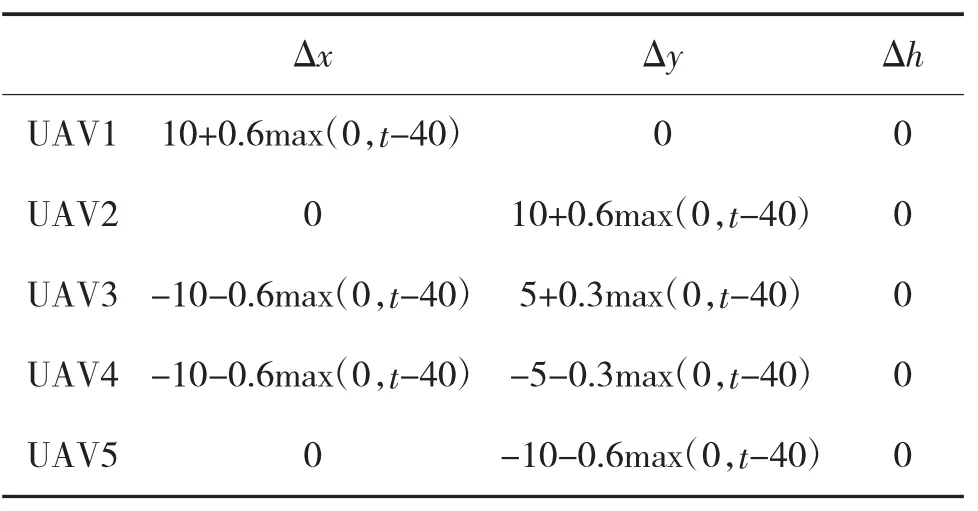
表3 编队距离期望路径的相对距离
所有多旋翼飞行器的实际轨迹如图2~图6 所示。由图可知,所有的无人机均沿着期望的路径运动,从小五边形编队变换大五边形编队。
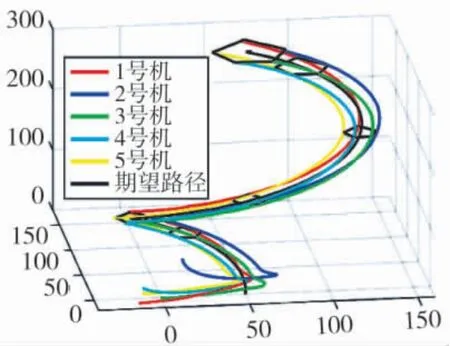
图2 无人机编队运动轨迹
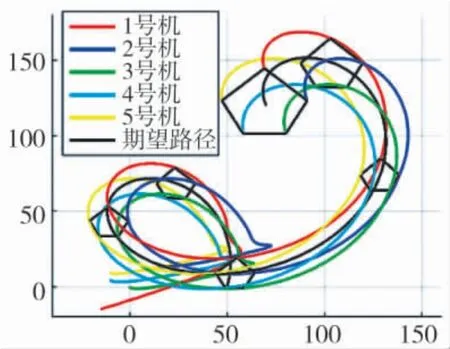
图3 无人机编队x-y 方向运动轨迹
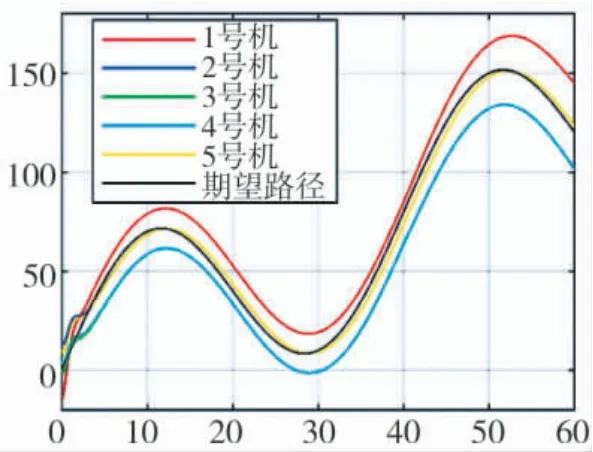
图4 无人机编队x 方向运动轨迹
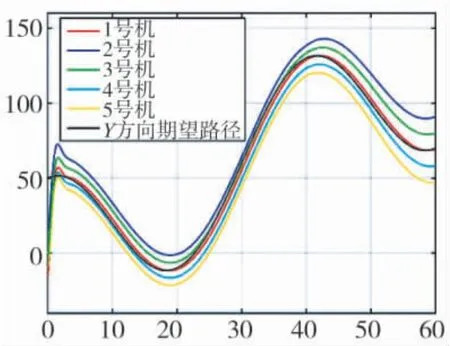
图5 无人机编队y 方向运动轨迹
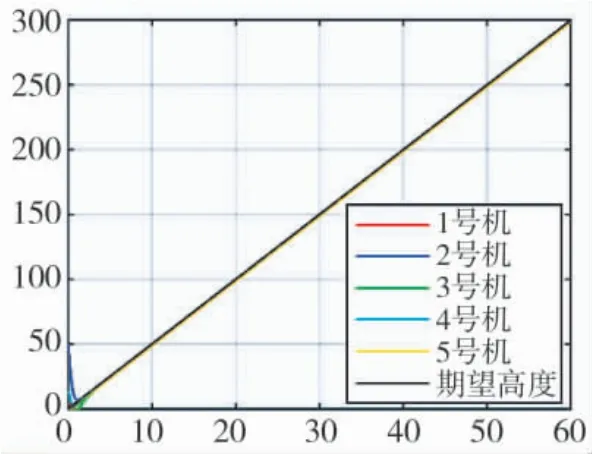
图6 无人机编队高度方向运动轨迹
图7~图9 给出了路径跟踪误差曲线。由图可知,路径跟踪误差可以收敛至一定范围内,这与式(31)的结果是一致的。
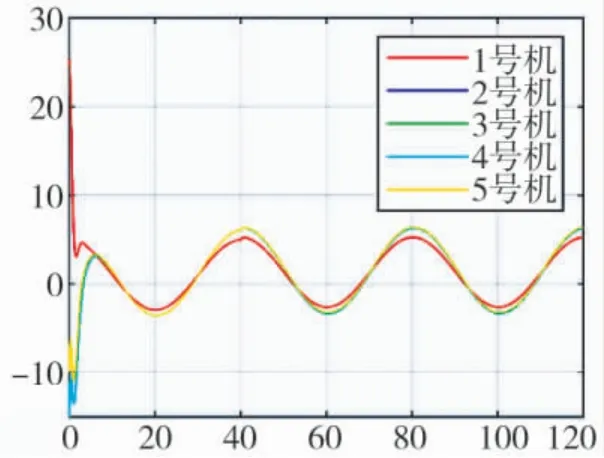
图7 无人机编队x 方向轨迹误差
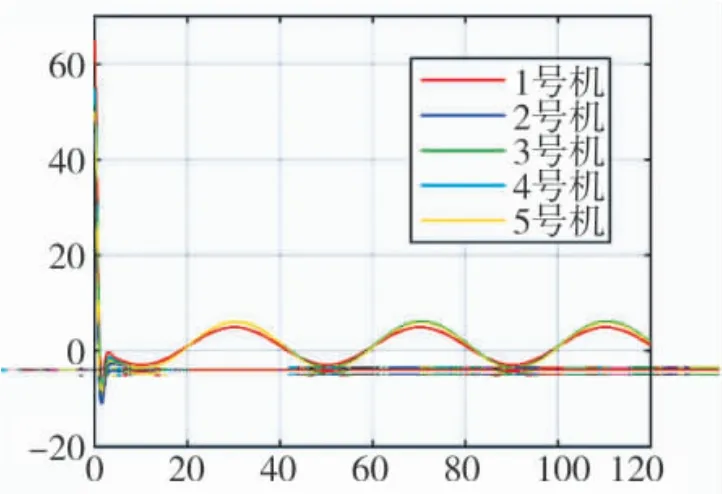
图8 无人机编队y 方向轨迹误差
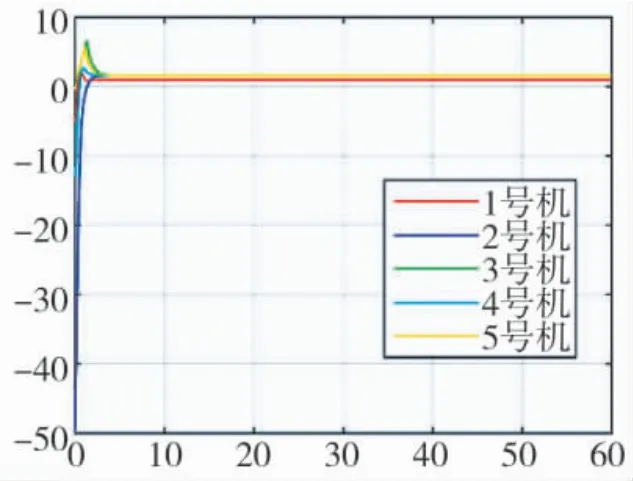
图9 无人机编队高度方向轨迹误差
5 结论
本文讨论了多旋翼飞行器的编队控制问题,建立了关于多旋翼飞行器的六态模型,并将其简化为一个二阶非线性模型。在此基础上,设计了一种基于均匀量化器的编队控制协议,并用代数图论和李雅普诺夫理论证明了误差系统的稳定性。最后,设计并实现了多旋翼飞行器编队的仿真实验。实验表明,系统能够快速形成期望编队,跟踪时变编队轨迹,以较小的稳态误差保持编队,运动规律平滑,当编队形状发生改变时,系统仍能实现稳定。实验结果验证了本文所设计编队控制协议的有效性。但由于本文所提出的控制方案未考虑多旋翼飞行器的偏航通道,以及偏航角度所带来的通道耦合问题,在以后的研究中还需进行相关的理论分析和实验验证。
