双峰谱波浪诱发细长港低频振荡的物理试验研究*
2020-11-09吴宏桥马小舟
王 敏,吴宏桥,何 波,马小舟
(1.中远海运港口有限公司,上海 200080 ;2.中交水运规划设计院有限公司,北京 100007;3.大连理工大学海岸和近海工程国家重点实验室,辽宁 大连 116024)
当特定的(与港湾本征频率一致的)低频波浪入射到港湾内部时,会被捕获于港湾内部并被显著放大,诱发港内水面大幅的波动,此现象即为港湾共振[1-3]。一般港池或系泊船系统共振响应周期在几分钟到1 h之间,而普通风浪的周期在秒的量级上,由于频率之间的巨大差距,风浪很难直接诱发港池发生共振,而是短波群通过波浪非线性将能量传递给周期与波群周期相近的低频波浪中,这些低频波浪与诱发港池共振密切相关[4-8]。当低频波浪周期与系泊船舶的自然摇摆周期或偏航周期一致时,会发生进一步的共振,这将导致系泊船舶或港池设施受损,从而导致港池作业的延误或产生昂贵的港池基础设施维修费,造成巨大的经济损失[9]。因此,准确预测低频波浪对港池共振响应的影响至关重要。
Longuet-Higgins等[10]在理论上证明了短波群在传播过程中会产生约束长波;Bowers等[11]首次将约束长波与港湾振荡联系起来;Dong等[12]利用2D-FUNWAVE完全非线性Boussinesq模型研究了短波频率对细长港内长波振荡的影响以及利用小波二阶相关谱分析了波-波非线性相互作用过程;王岗等[13]采用Boussinesq数值模型研究了双色短波波长对港池振荡的影响;Gao等[14-17]利用Boussinesq数值模型先后分析了双色短波频率,以及暗礁地形变化对细长港内约束长波和自由长波及其相对成分的影响。
当风浪和涌浪同时在某海域出现时,波浪频谱将呈现双峰,即低频的涌浪谱峰和频率较高的风浪谱峰。双峰谱在世界各地海域均有出现,例如秘鲁的钱凯湾、斯里兰卡的汉班托塔港海域、我国的东海都观测到类似波况。邓蔷[18]曾采用Boussinesq数值波浪模型,模拟双峰谱波浪作用下大窑湾水域的响应状况,然而目前关于双峰谱波浪诱发港湾振荡的研究分析较少。 本文通过物理模型试验研究了双峰谱中低频波浪(涌浪)周期和有效波高变化对诱发港池低频振荡的影响。与以往研究相比,主要有两方面的研究进展:一是首次利用物理模型试验研究了双峰谱波浪诱发细长港池低频振荡;二是首次利用平方小波二阶相关谱系统地分析了双峰谱波浪在港内发生的非线性能量传递过程。
1 试验设置
1.1 试验布局
试验在大连理工大学海岸和近海工程国家重点实验室波浪水池进行,水池长40 m、宽24 m、深1.2 m。试验布置见图1a),推板式造波机位于水池的东侧边壁处,水池的其它3个边壁处布有消浪网格栅用于吸收行进波,模型区域(4.8 m×3.2 m)位于水池的西南角,行进波水平自东向西传播。然而,当波浪模拟时间较长时,模型区域形成的反射波会在造波机处发生二次反射,为了降低二次反射波浪对试验结果的影响,充分发挥水池南北两侧消浪网格栅的消波作用,模型短边与入射波浪方向设置20°的夹角。细长港几何尺寸见图1b),港池长2.4 m、宽0.3 m,水深恒为0.6 m。图中灰色区域代表无水观察区域,用于更换仪器和近距离观察试验现象。波高仪布置见图1c),G1测点布置于港池底端中点,用于采集港内响应波浪;G2测点位于口门中央,将口门封闭时该测点采集到的双峰谱波浪作为入射波浪。试验采用的是标准电容式波高仪,量程为50 cm,测量精度为±0.1 mm,波浪到达港池底端时开始采集数据,采样间隔为0.02 s(50 Hz),采样点数为8 192个,波高是根据对相应测点位置的波面采用上跨零点法得到的,每个波况重复3次,确保试验数据的重复性。模型实物照片见图2,整个试验模型是由光滑的玻璃和方钢粘接而成。
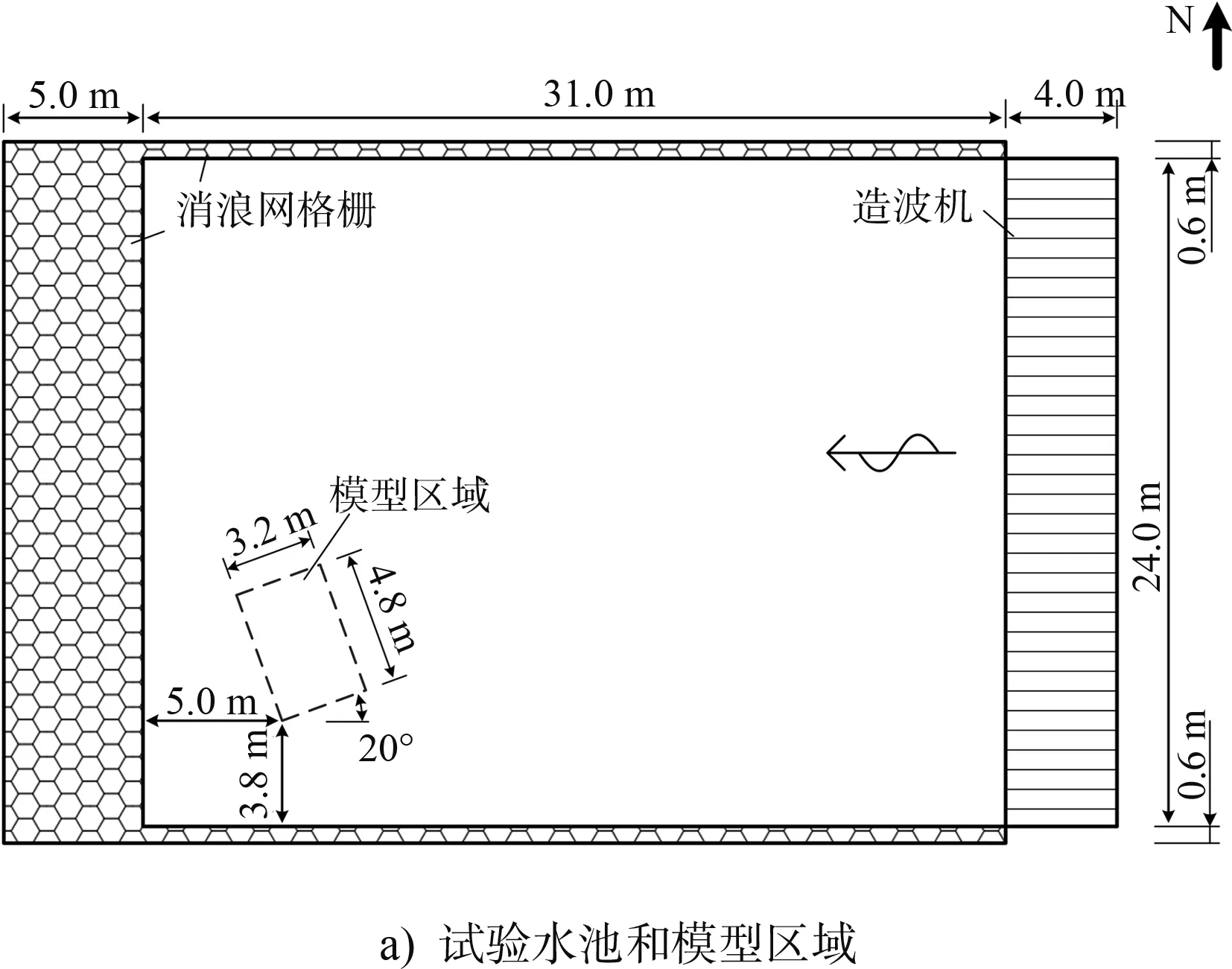
图1 试验布置

图2 模型实物
1.2 试验波况设置
1.2.1规则波波况
一般而言,一个港池的所有共振模态中,只有前几个共振模态波浪响应比较显著,试验中只研究该港池的前3个共振模态。因此,试验规则波周期设置范围为1.120 ~7.419 s,该波周期范围既覆盖了港池的前3个共振频率,同时又在造波机的能力范围内,入射波目标波高H0为0.04 m。
1.2.2双峰谱波况
双峰谱的入射谱形由两个Goda改进的JONSWAP单峰谱叠加而成,分为低频谱和高频谱两部分,其中单峰JONSWAP谱密度函数为:
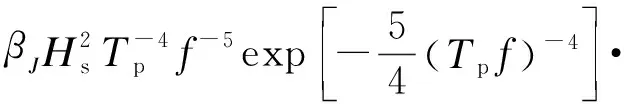
γexp[-(Tpf-1)2(2σ2)]
(1)
其中:

(1.094-0.019 15lnγ)
(2)
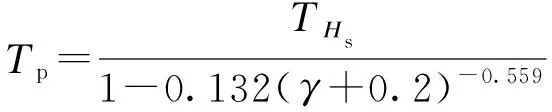

(3)
(4)
将两个JONSWAP谱合成一个双峰谱密度函数,表达式为:
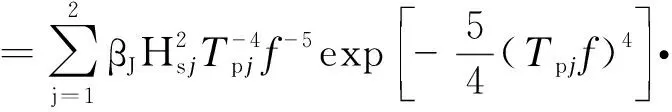
γexp[-(Tpjf-1)2(2σ2)]
(5)
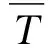
双峰谱试验参数见表 1,fp1变化范围为0.112 1~0.292 1 Hz,Hs1变化范围为0.003~0.015 m,fp2恒为0.694 4 Hz(非港池共振频率)、Hs2恒为0.04 m。A序列与B序列组合共设置7×4=28个双峰谱试验波况,用于研究fp1和Hs1变化对诱发港湾振荡的影响。需要说明的是,表1的试验参数指的是造波机输入值,实际入射波浪参数以G2测点采集的波浪数据为准。

表1 双峰谱波浪试验参数
2 试验结果分析
2.1 规则波响应曲线分析
取波面时间序列较稳定部分10~15个周期的均方根波高作为响应波高,放大因子定义式为:
Rf=HR(f)[2H0(f)]
(6)
式中:f为频率;Rf为不同频率波浪的放大因子;HR(f)和H0(f)分别为不同频率波浪的响应波高和入射波高。规则波放大因子响应曲线见图3,其中理论响应曲线是根据Mei[20]的线性解析解计算得到的,试验结果与理论结果吻合很好。为了降低试验结果误差,利用双曲正割函数的平方对放大因子试验数据进行拟合,其中拟合函数为:
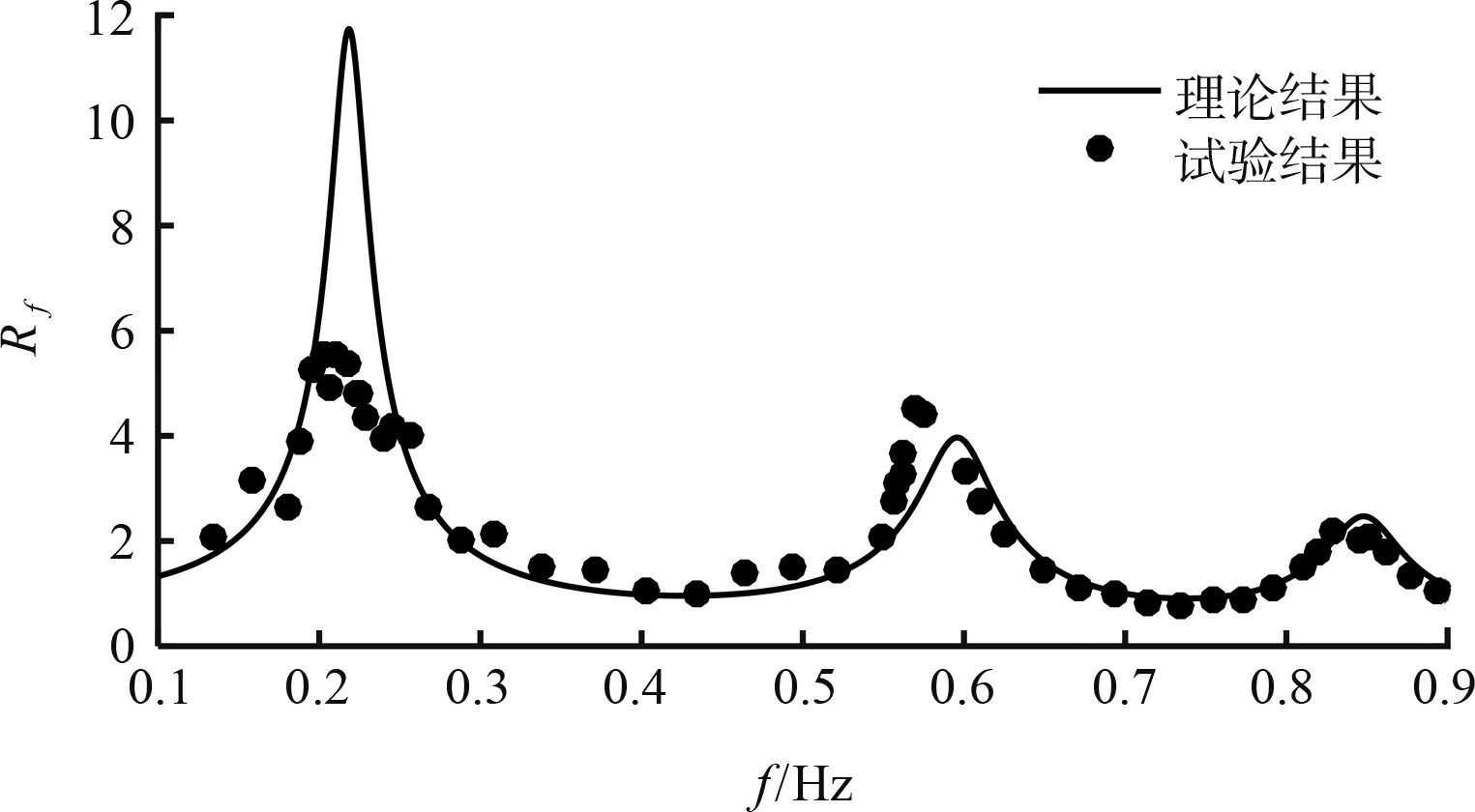
图3 规则波放大因子
f=asech2[b(x-c)]+d
(7)
式中:a、b、c和d是未知变量,通过最小二乘法进行计算并确定相应的值。其中坐标(c,a+d)为拟合函数的一个极值点,分别为拟合共振频率以及对应的放大因子。前3个共振模态的拟合曲线见图4,根据拟合结果确定的港池前3个共振频率分别为0.214、0.582、0.840 Hz。共振频率的解析解为0.218 、0.597 、0.845 Hz,拟合结果与理论结果之间误差很小,因此,通过规则波试验结果准确识别出了该港池前3个模态的共振频率。
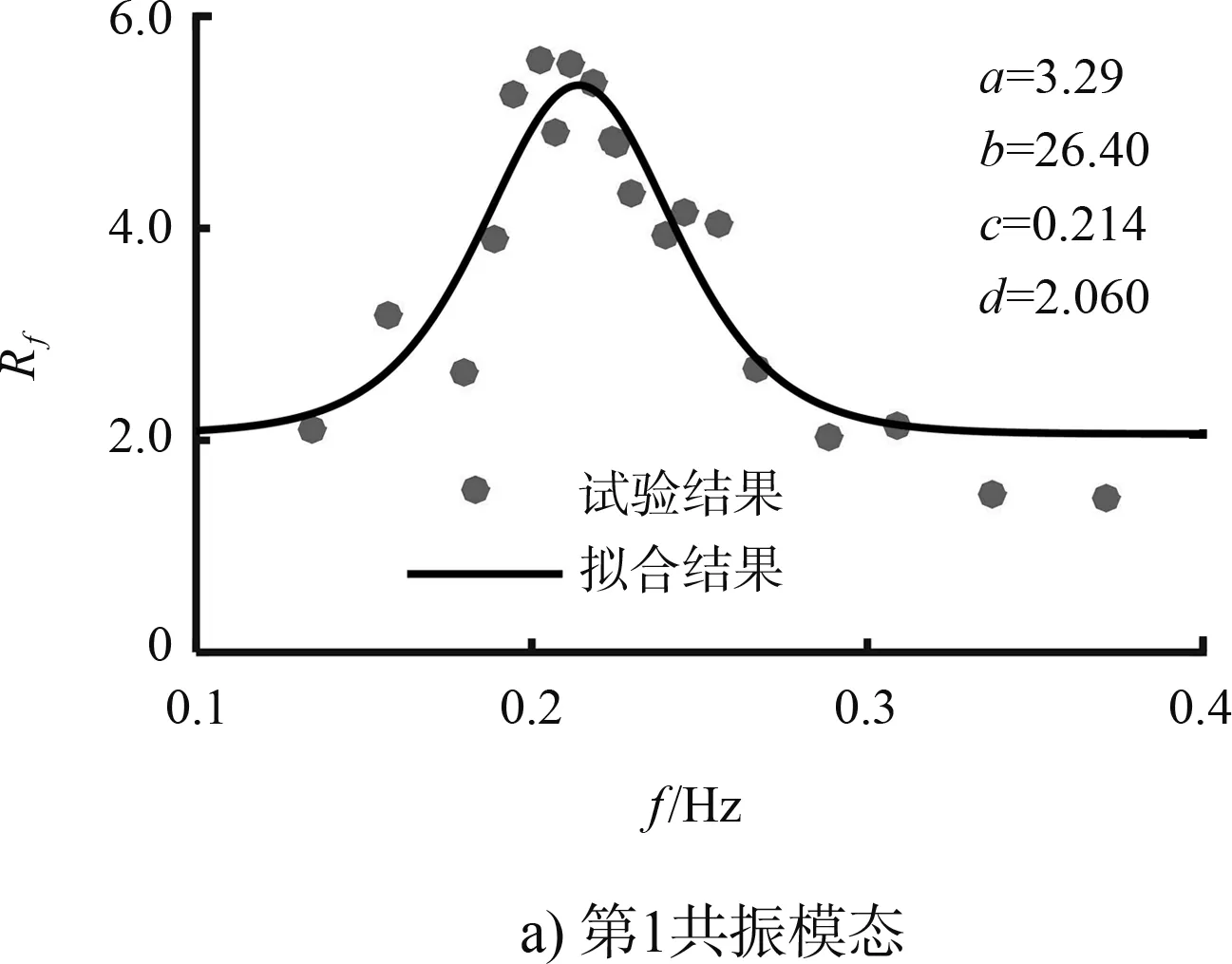
图4 放大因子拟合曲线
2.2 双峰谱波浪的能量谱分析
试验给出了A1B4~A6B4共6个波况的入射波和相应的响应波浪的频谱对比,见图5。可以看出,波浪在港内响应过程中,不同频率波浪之间存在明显的能量传递,尤其是高频谱波浪将大部分的能量传递到低频波浪中,使得fp1即使与第1共振频率相差很大,也明显诱发了第1共振模态的波浪振荡,见图5a)~5b)。 还可看出,虽然入射波谱中Hs1小于Hs2,但随着fp1的大小逐渐接近第1共振频率,第1共振频率附近的波浪(低频波浪)响应显著增强,其响应程度远强于高频波浪的响应图,见5b)~5f),而高频波浪主要在第2和第3共振模态附近有较弱的响应。
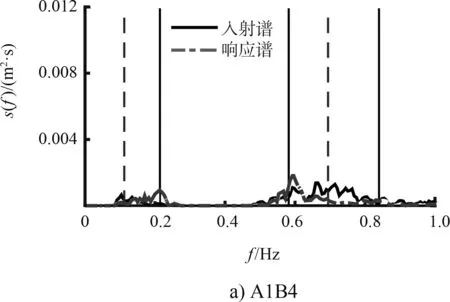
注:虚竖线标记了2个入射谱峰,实竖线标记了由规则波放大因子曲线确定的该港池的前3个共振频率。为了便于观察,图中的入射谱值是实际入射谱的5倍。
图6是图5波况对应的Morlet小波能量谱,根据小波能量谱可以直观看出不同频率的波浪能量随时间的变化过程[21]。可以看出,谱峰fp1和fp2的波浪能量明显向第1和第2共振频率波浪传递。从波浪能量增长时间看,随着fp1的逐渐增大,第1共振频率波浪能量增长速度逐渐加快,拥有显著能量的所需时间从80 s缩减到30 s再到10 s,见图6a)~6c)。甚至波浪刚到达港池底端,就伴随着可观的波浪能量,见图6e)。同时不同频率波浪能量增长并不是持续的,彼此之间一直处于动态的能量交换中。
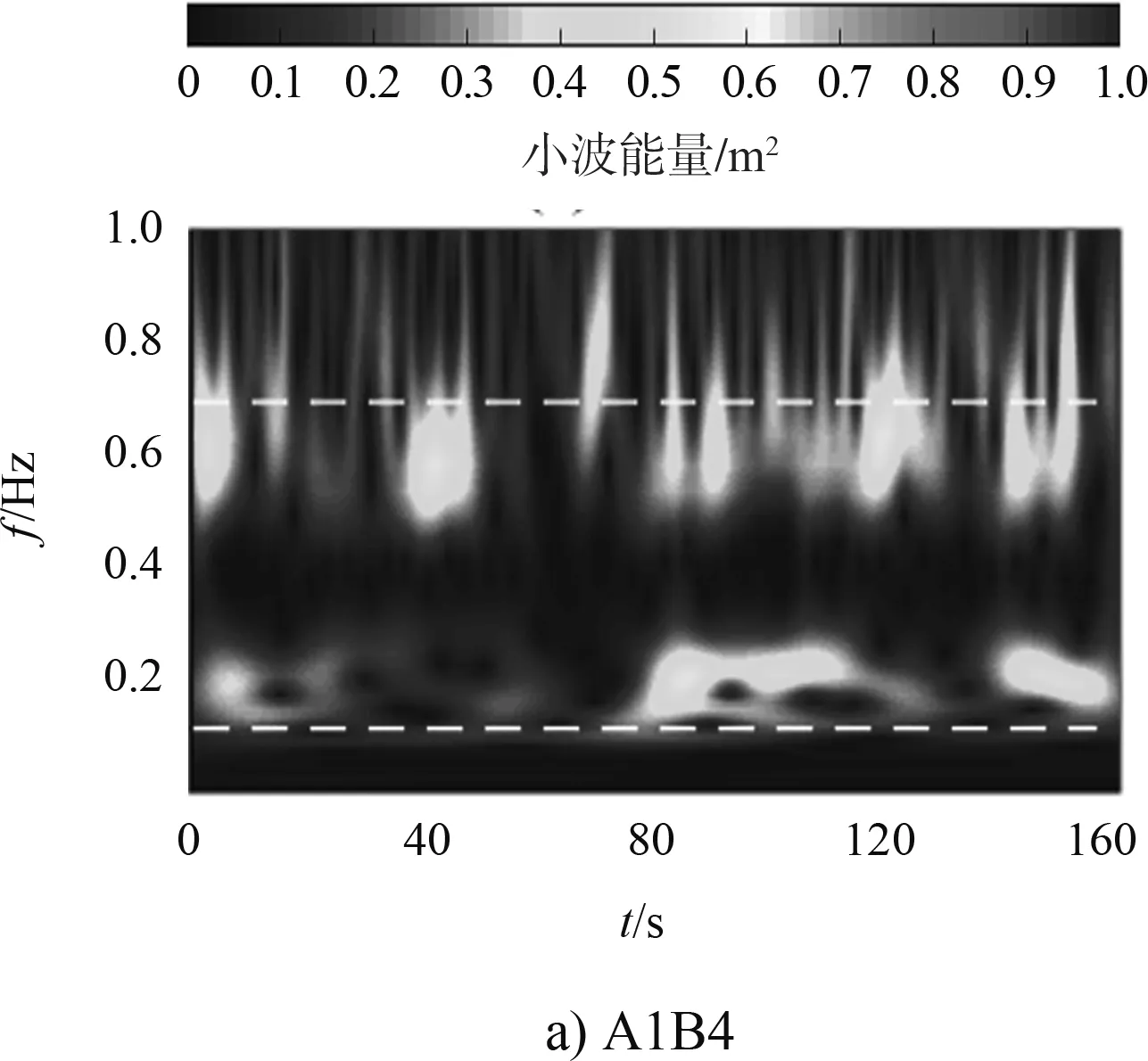
注:虚线代表谱峰初始频率位置。
2.3 双峰谱波浪的共振响应分析
2.3.1低频谱峰的响应分析
根据上节谱分析可知,不同fp1的波浪在港内响应程度不同,本节通过fp1的放大因子曲线,定量分析不同fp1的波高在港内的响应程度。首先给出双峰谱波高放大因子计算公式[22]:
Rf=HR(f)[HI(f)]
(8)
式中:Rf为不同频率波浪的放大因子;HR(f)和HI(f)分别为不同频率波浪的响应波高和入射波高。
图7给出了4组不同Hs1下fp1的放大因子曲线与理论放大因子曲线的对比。可以看出,fp1接近第1共振频率时,fp1对应的放大因子明显增大;远离共振频率时,相应的放大因子较小,与理论放大因子曲线变化趋势相一致。同时还可以看出,Hs1对fp1放大因子的影响主要体现在共振频率附近的波况中,整体上看fp1的放大因子大小与Hs1成反比。
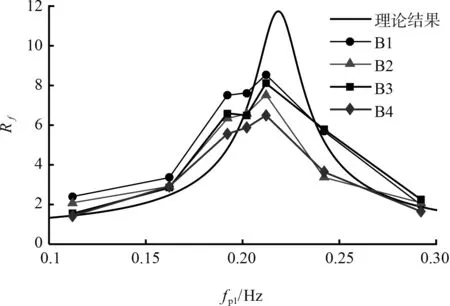
图7 B1~B4波况fp1放大因子对比
为了能够根据fp1放大因子结果更加准确地识别出该港池的第1共振频率,利用上文提到的拟合函数(式(7)),对试验数据进行拟合,结果见图8。由这4组波况拟合得到的第1共振频率在0.208 0~0.216 2 Hz,理论解为0.218 Hz,试验结果与理论值之间的误差主要是由于试验过程中波浪能量损失造成的。因此,利用fp1放大因子曲线可以准确识别出该港池的第1共振频率。
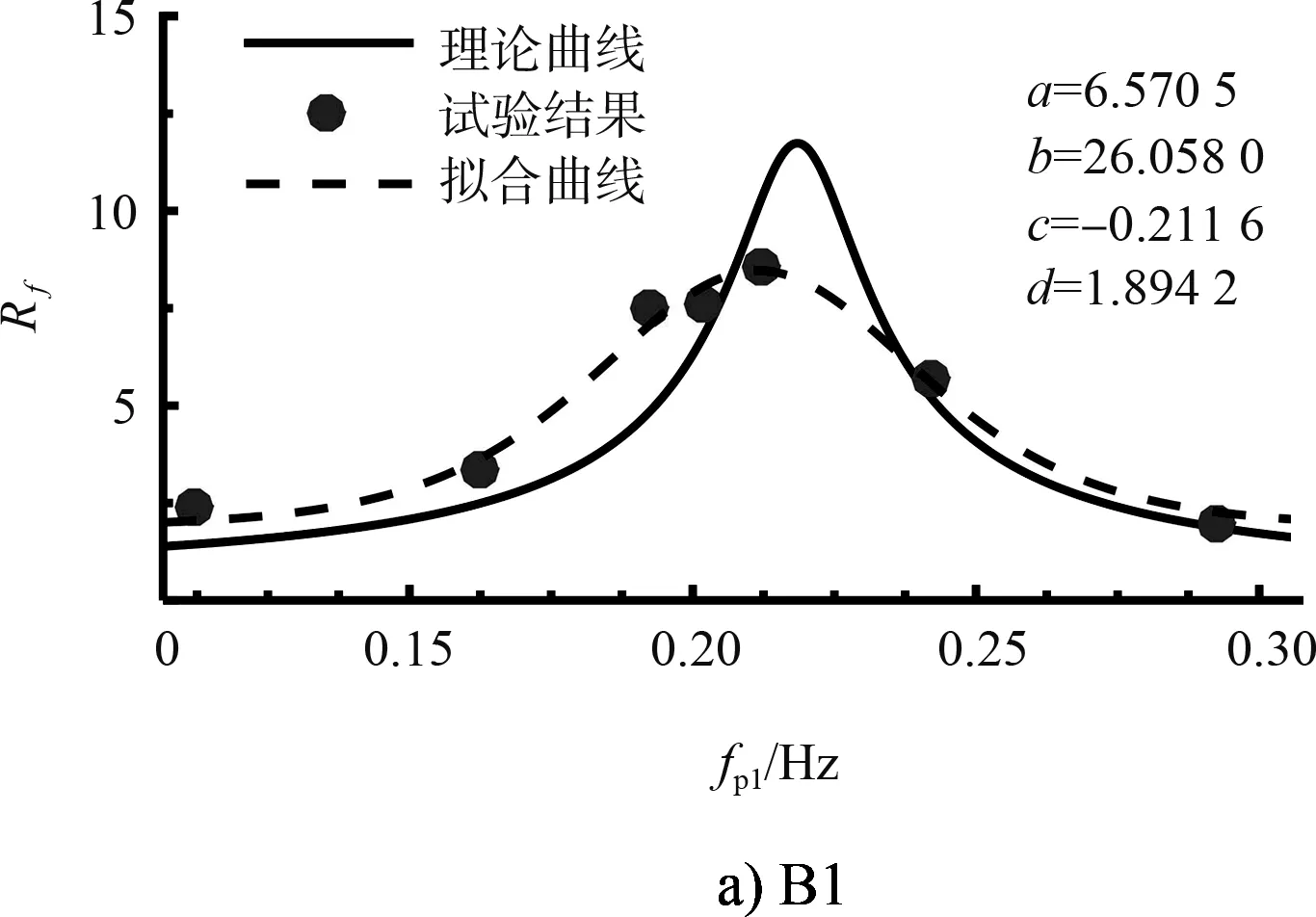
图8 B1~B4波况fp1放大因子拟合曲线
2.3.2fp1和Hs1对共振模态波浪响应的影响分析
不同Hs1情况下,fp1的大小对港内前3个共振模态波浪响应的影响见图9,其中纵坐标Rj(fp1)(j=1,2,3)代表不同fp1下,第1、2、3共振频率波浪的放大因子。可以看出,Hs1对第1共振模态波浪响应影响最为明显,不同Hs1波况下的放大因子差别很大,并且Hs1对其影响的规律性不是很强。而不同Hs1波况对于第2和第3共振模态放大因子影响很小,不同曲线几乎重合在一起。同样,fp1对第1共振模态波浪的影响也没有规律性可寻;第2共振模态的放大因子随fp1的增长几乎呈水平直线变化,即第2共振模态的波浪响应不受fp1变化的影响;同样,只有fp1接近第1共振频率时对第3共振模态波浪响应才会显著增强。
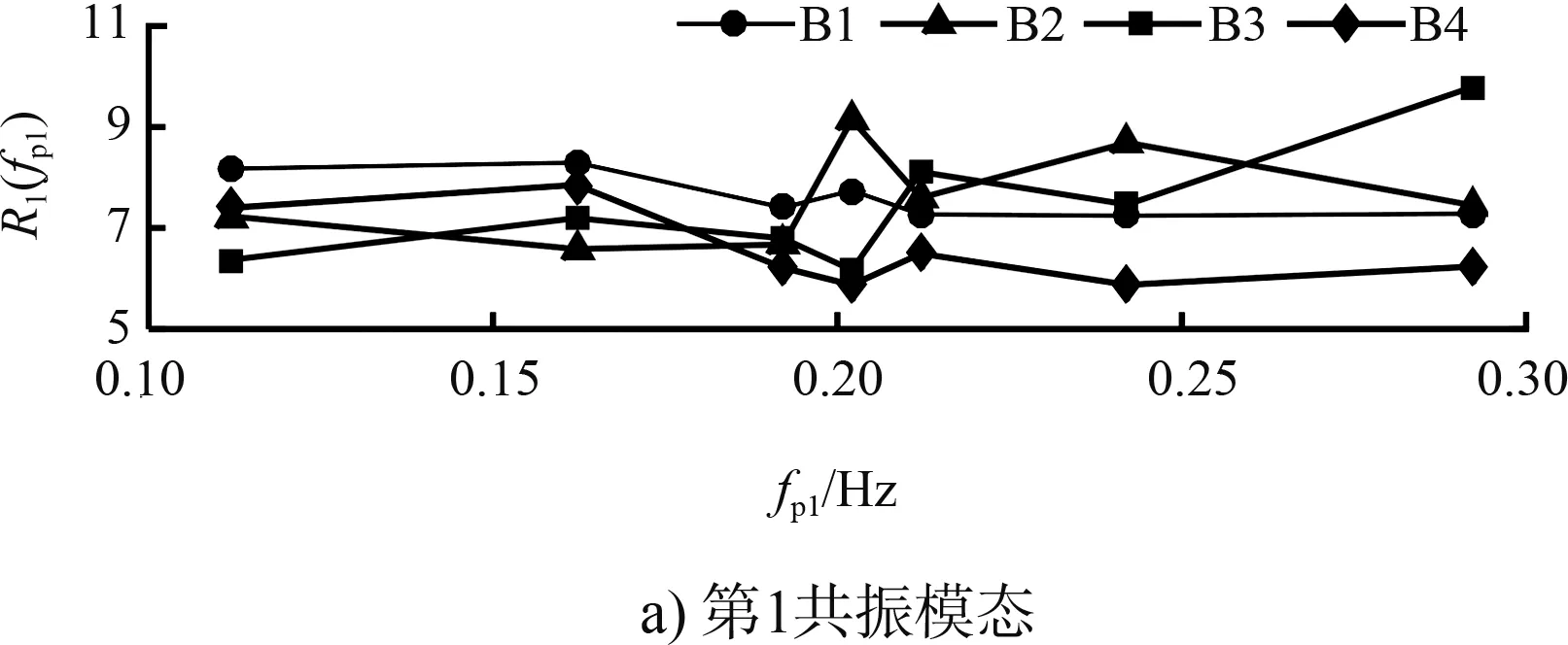
图9 B1~B4波况前3共振模态放大因子对比
2.4 双峰谱波浪的非线性分析
从波浪谱分析得知,第1共振频率波浪能量在港内有显著的增长,主要原因是高频波浪通过波浪之间复杂的非线性相互作用将能量传递到低频波浪中去。本文利用平方小波二阶相关谱可以反映出波浪之间非线性相互作用程度这一特性,平方小波二阶相关谱表达式为[23]:
(9)
f1+f2=f3
(10)
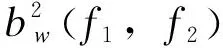
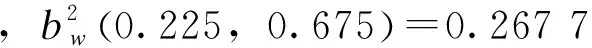

图10 不同fp1的平方小波二阶相关谱
其次进一步分析Hs1对港内双峰谱波浪之间非线性的影响,以A5B1~A5B4共4个波况为例,图11给出了该4组波浪的平方小波二阶相关谱。从图11可以定性地看出,港内波浪非线性主要发生在fp1、fp2及fp1、第3共振频率的波浪之间,随着Hs1的增大,fp1、fp2及fp1、第3共振频率波浪之间非线性相互作用均逐渐增强的同时,fp1附近的波浪与fp2波浪之间发生较强的波浪非线性相互作用,逐渐向fp1附近的波浪与第3共振频率附近的波浪发生较强的非线性相互作用过渡,见图11。
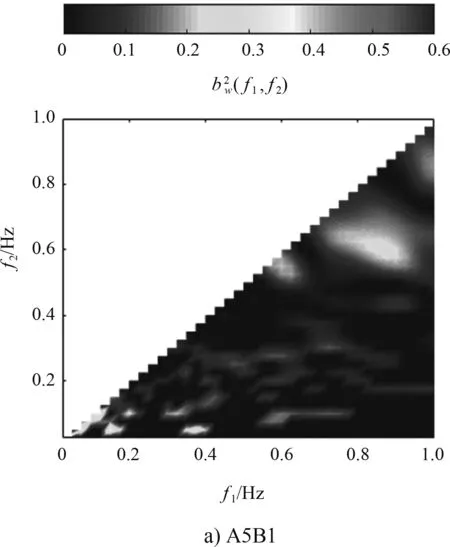
图11 不同有效波高Hs1的平方小波二阶相关谱
3 结论
1)不同fp1的双峰谱波浪均可诱发港池第1共振模态的振荡,fp1越接近于港池的第1共振频率,低频波浪在港内响应越剧烈,即便入射波中Hs1小于Hs2,港内低频波浪响应也要明显强于高频波浪的响应。同时根据fp1放大因子曲线可以准确地识别出该港池第1共振频率
2)双峰谱波浪中fp1和Hs1的大小对港池第1共振模态波浪响应影响较大,对第2共振模态波浪的响应几乎没有影响,只有当fp1接近港池第1共振频率时,对第3共振模态波浪响应影响才会显现出来。
3)通过平方小波二阶相关谱对港内波浪非线性分析发现,当fp1接近第1共振频率时,港内波浪非线性相互作用较剧烈,波浪之间能量传递较多。随着Hs1的增大,fp1、fp2及fp1、第3共振频率波浪之间非线性相互作用均逐渐增强的同时,fp1附近的波浪与fp2波浪之间发生较强的波浪非线性相互作用,逐渐向fp1附近的波浪与第3共振频率附近的波浪发生较强的非线性相互作用过渡。
4)以上研究结果是针对双峰谱作用于规则形状的细长港池开展的,其作用机理对于涌浪和风浪长期共存的海域港口,例如秘鲁钱凯湾建设中的中远海运钱凯港一期工程起到良好的指导作用。
