轻质沙沙波形态水槽试验研究

2020-11-09王晓旭高清洋徐俊锋

水运工程 2020年9期

王晓旭，高清洋，徐俊锋

(1.天津水运工程勘察设计院，天津300456；2.中交天津港湾工程设计院有限公司，天津 300461；3.交通运输部天津水运工程科学研究所，天津 300456)

水利水运工程事关社稷民生，针对我国江河中泥沙输移及河床冲淤演变的研究复杂而持久，借助河工动床模型进行试验模拟是此类问题研究及验证的可靠手段之一。理论上，动床模型试验须满足水流泥沙的动力相似、运动相似及河床形态的几何相似等，关键是合理选择模型沙。在模拟沙质推移质时，当试验流速较小，按起动相似准则选用的天然沙通常黏结力较大，使得试验结果与实际不符。因此现阶段动床模型通常选用密度较小、粒径较大的轻质沙替代天然沙，从而使模型沙的起动相似和河床变形相似。然而动床模型试验中，在满足相似性条件基础上，仍可能会出现轻质沙沙波在一定程度上的异常发育现象，这一偏差将影响阻力相似及水流、泥沙运动状态[1-3]。

沙波是床面形态的一种表现形式，流体剪切力作用在由松散颗粒堆积的床面上，使得泥沙颗粒群体产生有规律的运动，进而在床面上呈现出具有一定特征规律的床面形态[4]。因此可将影响沙波运动的因素分为水动力条件及泥沙颗粒自身的物理和运动特性两方面。前者表征参数主要包括Fr(弗劳德数)、水流运动强度UUc(其中U为流速，Uc为泥沙起动流速，两者均为垂线平均流速)等；后者表征参数主要包括粒径、表观形状、床沙级配组成、泥沙的孔隙率、水下休止角等。前人研究成果丰富，长办汉口河道观测队、张柏年[5]、张瑞瑾[6]及詹义正等[7]各自建立了沙波波高与UUc的关系，均能客观反映沙波形态随水流强度变化的规律，然而上述公式多为基于实测并经修正的经验公式，在采用轻质沙的动床模型试验应用上存在一定限制。因此针对影响轻质沙沙波形态的主要因素开展研究，厘清相互关系，进而在合理范围内有效扼制沙波异常发育，有助于进一步认识轻质沙河床阻力及沙波机理，且对提高动床模型试验精度及更加科学合理地指导工程有重要意义。

1 试验思路及布置

试验在天津水运工程科学研究所试验大厅的水槽内进行，水槽总长约25 m、宽0.9 m、高1 m，水槽中部为试验段，长约10 m，试验段左岸岸壁侧设置钢化玻璃，便于观察和记录，见图1。建立三维坐标系，x轴平行于水流方向，以试验段起始点为零点，沿水流方向为正；水平方向垂直于水流方向为y轴，以水槽中垂线处为零点，向左岸岸壁侧为正；铅垂方向为z轴，以试验段起始点的平床床面为零点，垂向向上为正。试验段沿程布置各类所需仪器设备。

注：W为侧收缩型矩形薄壁堰，M为移动测架，D为尾门，V为ADV流速仪。

研究选用沙波波高及波长作为沙波形态的表现指标，并采用控制变量法，选用对沙波形态影响较大的密度、中值粒径D50(简称“粒径”)、Fr及UUc等表征参数开展分析，水流强度调节主要通过调整入流流量及试验段水深的方式。为便于数据观测，在确保试验沙波平稳发育、泥沙平稳输移的基础上，通过参照前人试验参数、观测前期预备试验及验证计算床面无量纲切应力，得到试验条件，见表1。

表1 试验组数

2 沙波波高试验分析

2.1 沙波波高与Fr的关系

一般情况下，沙波波高采用无量纲的相对波高Δh来表示，其中Δ为波高，h为水深。由于Fr(Fr=u(gh)0.5)为明渠水流在某特定断面上的惯性作用与重力作用之比，决定水流流态且与沙波的形成及发育紧密相关，故本节采用Fr作为水流动力条件的表征参数，探究相对波高Δh与Fr的关系。

1)由图2可知，本试验Fr在 0.10～0.32变化范围内，伴随Fr增加，相同密度、相同粒径下的相对波高Δh逐渐增大，其中较小密度的轻质沙在Fr较大的时相对波高Δh的增长趋势趋于平缓，而较大密度的轻质沙则仍不断增长，该过程与床面沙波初始阶段的发展趋势适应。

2)探讨轻质沙粒径与相对波高、Fr的关系时，图2表明粒径的不同对于相对波高与Fr的影响不显著。

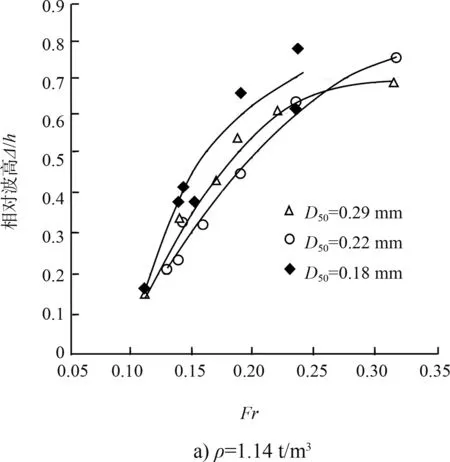
图2 不同粒径轻质沙Δh与Fr关系

3)探讨轻质沙密度与相对波高、Fr的关系时，不须考虑粒径的影响，前人多采用无量纲的波高粒径比ΔD来表示沙波波高特征值，其中Δ为波高，D为粒径直径。由图3可知，在本试验Fr在0.10～0.32变化范围内时，当Fr一定时，轻质沙密度越大，波高粒径比ΔD越小。

图3 不同密度轻质沙波高粒径比ΔD与Fr的关系

综上，Fr在 0.10～0.32变化范围内，利用Fr作为水流动力条件参数表征沙波波高、粒径、密度的关系存在一定限制。

2.2 沙波波高与UUc的关系

除Fr外，前人同样采用无量纲的水流运动强度UUc作为水流动力条件的表征参数，其中Uc采用武汉水电学院公式[8]计算所得，公式如下：

Uc=(hD)0.14[1.76(ρs-ρ)Dρ+

6.05×10-7×(10+h)D0.72]0.5

(1)

式中：ρs和ρ分别为泥沙的密度和水的密度；D为泥沙粒径；h为水深。

1)由图4可知，本试验UUc在0.8～2.5变化范围内，伴随着UUc增加，相同密度、相同粒径下的相对波高Δh逐渐增大，其中较小密度的轻质沙在UUc较大时，相对波高Δh的增长趋势有所减弱，而较大密度的轻质沙则仍有不断增长的趋势，该过程与床面沙波初始阶段的发展趋势适应。

2)图4表明在同一密度条件下，当UUc相同时，随着轻质沙粒径增大，相对波高减小。

图4 不同粒径轻质沙Δh与Fr关系

3)由图5可知，本试验UUc在0.8～2.5变化范围内时，当UUc一定，轻质沙密度越大，波高粒径比ΔD越小。

图5 不同密度时ΔD与UUc关系

总的来看，UUc在0.8～2.5变化范围内，利用UUc作为水流动力条件参数表征沙波波高、粒径、密度的关系相对明确。

3 沙波波长试验分析

3.1 沙波波长λD与Fr的关系

一般情况下，沙波波长采用无量纲的波长粒径比λD表示，其中λ为波长，D为粒径。采用Fr作为水流动力条件的表征参数。

1)由图6可知，本试验Fr在0.10～0.32变化范围内，伴随Fr增加，相同密度、相同粒径下的波长粒径比λD均出现先增大后减小的现象。

2)图6表明在同一密度条件下，当Fr相同，随着粒径增大，波长粒径比λD减小。

图6 不同密度轻质沙λD与Fr关系

3)由图7可知，在本试验Fr=0.10～0.32变化范围内时，当Fr一定，密度的不同对于波长粒径比与Fr的影响不显著。

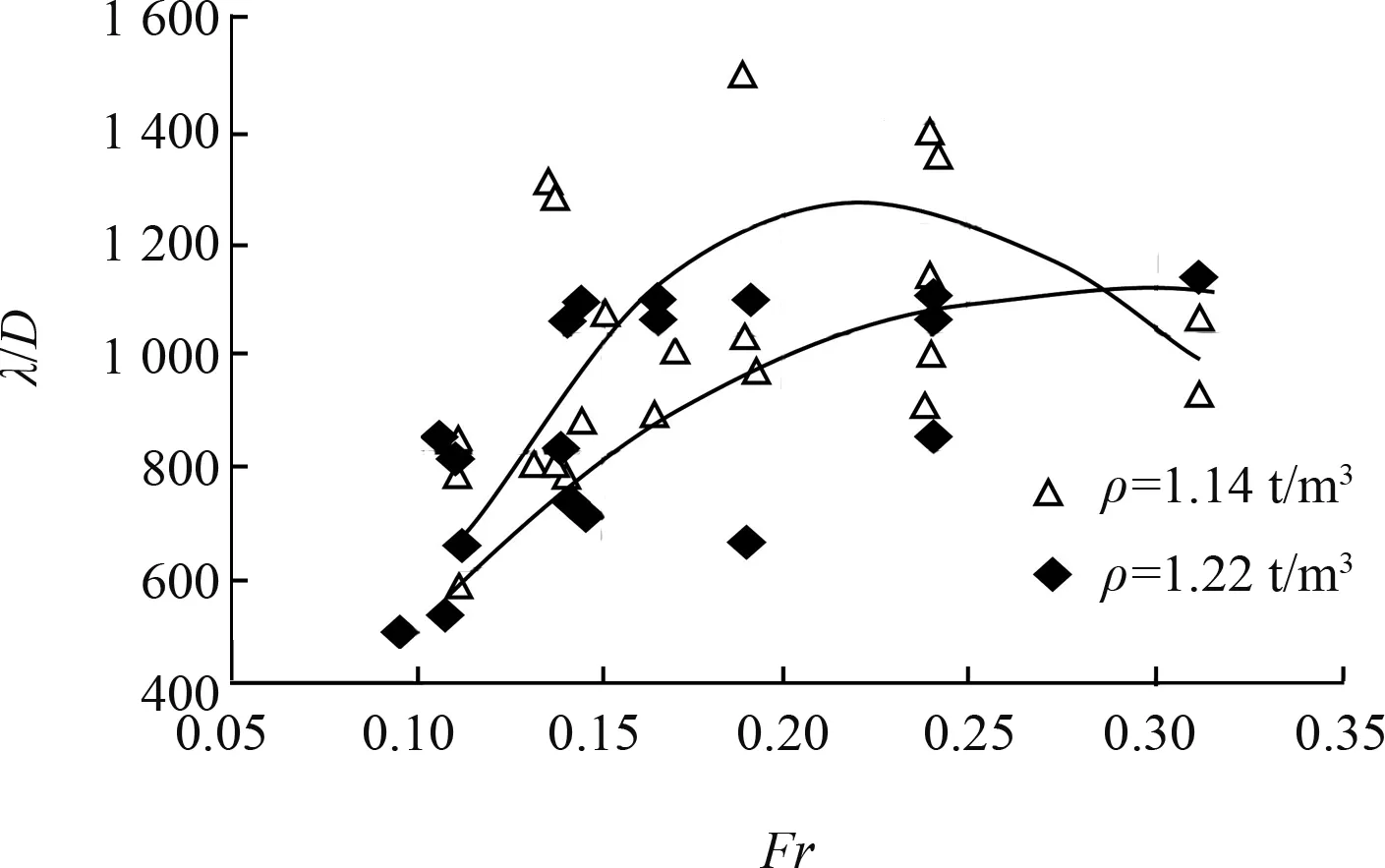
图7 不同密度时λD与Fr关系

总的来看，Fr在0.1～0.32变化范围内，利用Fr作为水流动力条件参数表征沙波波高、粒径、密度的关系存在一定限制。

3.2 沙波波长与UUc的关系

1)由图8可知，本试验UUc在0.8～2.5变化范围内，伴随UUc增加，相同密度、相同粒径下的波长粒径比λD均出现先增大后减小的现象。

2)图8表明，在同一密度条件下，当UUc相同，随着粒径增大，波长粒径比λD减小。

图8 不同密度轻质沙λD与UUc关系

3)由图9可知，本试验UUc在0.8～2.5变化范围内时，当UUc一定，轻质沙密度越大，波长粒径比λD越小。

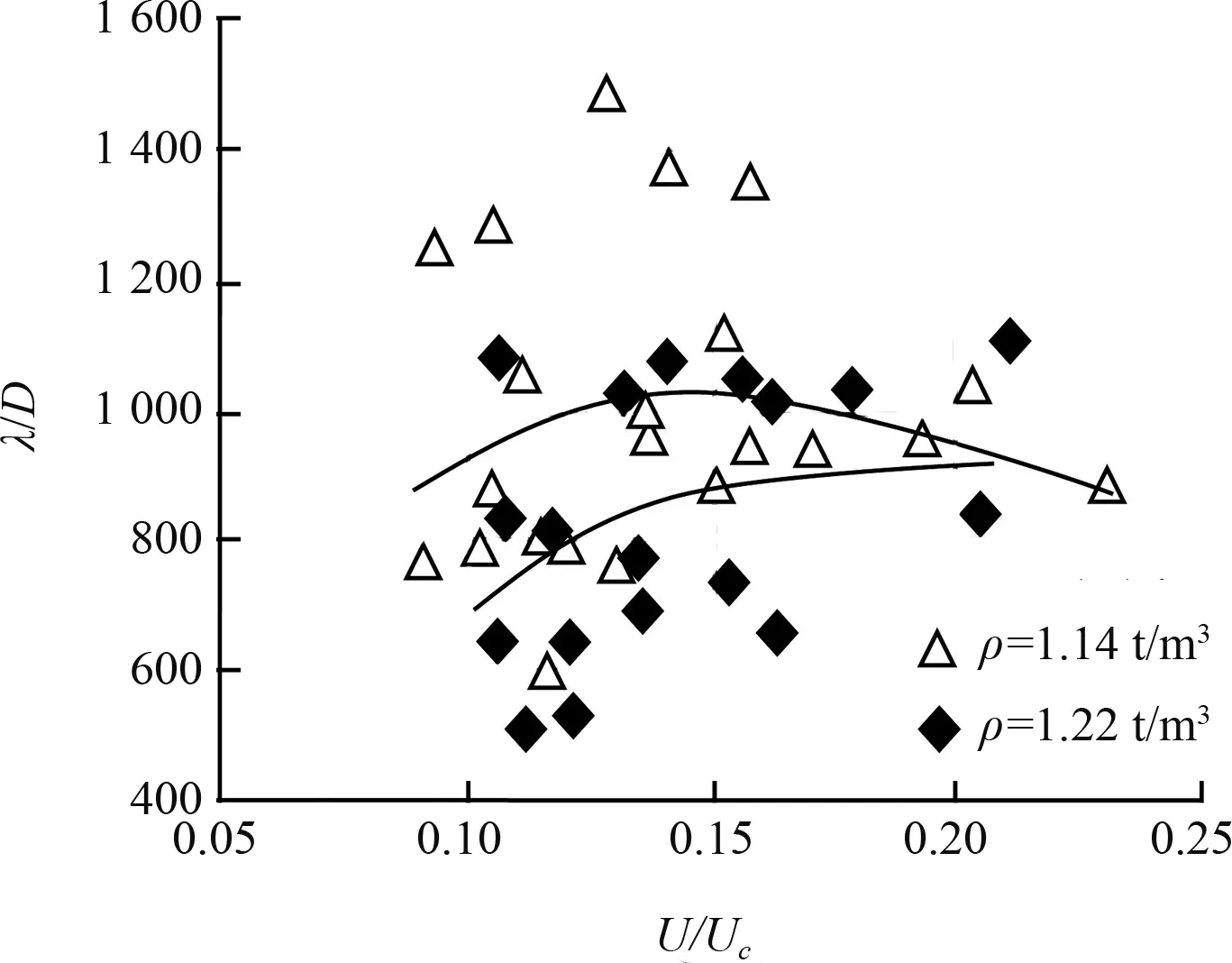
图9 不同密度时λD与UUc关系

总的来看，UUc在0.8～2.5变化范围内，利用UUc作为水流动力条件参数表征沙波波高、粒径、密度的关系相对明确。试验结论见表2。

表2 试验结论

由表2可知，在本试验条件下，采用Fr及UUc这两个表征参数均可在一定范围内反映轻质沙沙波形态变化与水流强度的关系，且整体趋势基本一致。然而当采用Fr时，粒径的不同对于相对波高Δh与Fr的影响不显著，密度的不同对于波长粒径比λD与Fr的影响不显著，表明采用该参数存在一定限制，而UUc可更全面地表达其与轻质沙沙波形态的变化关系。这可能是由于沙波是一种复杂、动态的水沙作用综合表现形式，而Fr仅表达流体惯性力与自重的关系，UUc则在此基础上还涵盖了泥沙粒径及密度等相关物理参数，因此在本试验条件下，利用UUc可相对更为显著地表达其与轻质沙沙波形态的关系。除此之外，若采用UUc表达，在其它条件不变的情况下，增大轻质沙粒径及密度，均可使相对波高及波长粒径比减小。

4 模型沙公式拟合分析

前人针对沙波形态的研究成果丰富。早在1960年，长办汉口河道观测队曾对长江沙波的波高Δ提出公式如下：

(2)

张柏年根据长江实测资料建立了波高公式如下：

(3)

早期张瑞瑾应用长江实测资料建立了沙波相对高度(Δh)与佛汝德数关系，公式如下：

(4)

将沙莫夫公式代入，得张瑞瑾修正公式：

(5)

詹义正等根据张柏年对长江资料的分析成果，通过微动量变化对比分析得出公式如下：

(6)

式中：Δ(或hs)为沙波波高；U为流速；Uc为起动流速；d为泥沙粒径；h为水深；A=0.53；B=0.135；C=3。

前人公式客观反映沙波形态随水流强度变化的规律，然而多为基于实测并经修正的经验公式，部分存在因次不和谐的问题，直接应用于轻质沙试验存在限制。将试验数据与张瑞瑾公式、张瑞瑾修正公式、詹义正公式计算值相比较，见图10，发现试验值均比公式计算值要大，但从发展趋势来看，试验数据与詹义正公式演变规律相似，故利用式(6)拟合本试验相对波高。将试验数据代入拟合，拟合结果为A=1.50，B=0.18，C=3.80，公式如下：