一种基于广义Petersen图的互联网络拓扑结构研究

李文升，岳孟田，李同胜，冯志芳

(廊坊师范学院理学院，河北廊坊 065000)

随着并行处理规模的不断扩大，为了进一步提高并行计算机的通信效率，人们一直在追求结构简单，节点度小，网络直径小的并行计算机网络模型。广义Petersen 图为3 正则图，节点的度均为3，因而其可用于构造并行计算机互联网络模型。Ohring 等提出了一种k维FPN 网络(Folded Petersen Network)。一个FPk网络包括5k个节点，也就是k个Petersen 图的笛卡尔积[1]。Das 等把Petersen 图嵌入Hypercube 网络,构造了一种HP 网络(Hyper Petersen Network)。因为HP 网络有非常小的直径,所以有很好的通讯效率[2]。Ohring 等把Hypercube 与Petersen图做笛卡尔积，构造了一种FPQn,k网络并分析了其容错性和可靠性,给出了路由算法[3]。刘宏英等[4]分析了RCP(n)互联网络并给出了基于该网络的组播路由算法。刘方爱等和邢长明等分别构造了RP(k)和RPC(k)互联网络并给出了对应的路由算法[5-7]。主要构造了一类基于广义Petersen 图GP(n,k)的互联网络结构EGP(k3,k2,k)，并分析了EGP(k3,k2,k)的直径和良好的通信性能。

1 预备知识

设G=(V,E) 为简单连通无向图。对任意的u,v∈V(G),dG(u,v)表示G中(u-v)最短路的长度，在不引起混淆的情况下，简记为d(u,v)。对任意的v∈V(G)和S⊆V(G),顶点v到点集S的距离为d(v,S)=min{d(v,u)|u∈S}。对任意的S⊆V(G)和T⊆V(G),点集S到点集T的距离为d(S,T)=min{d(u,v)|u∈S,v∈T}。

定义1设n和k为两个正整数，且n＞2k，广义Petersen图P(n,k)共含有2n个顶点，其顶点集为

V(P(n,k))={ui,wi|1≤i≤n}。

边集为

E(P(n,k))={uiui+1,uiwi,wiwi+k|1≤i≤n,下标模n}[8]。

定义2设n,k,t为正整数，且n＞2k,k＞t，拓展的广义Petersen 图(Expended Generalized Petersen Graphs)EGP(n,k,t)共含有2n个顶点，其顶点集为

V(EGP(n,k,t))={ui,wi|1≤i≤n},

边集为

E(EGP(n,k,t))={uiui+1,uiwi,wiwi+k,wiwi+t|1 ≤i≤n,下标模}n。

EGP(n,k,t)的构造方法：对于P(n,t)，在顶点wi和wi+k间连接边，其中i=pt,0≤p≤且p为整数，下标模n。

2 EGP(t3,t2,t)互联网络

讨论一类特殊的EGP(n,k,t)，即EGP(t3,t2,t)(t≥2)网络，设

则U,W,T为EGP(t3,t2,t)的三个圈，t=3 时的EGP(33,32,3)如图1所示。

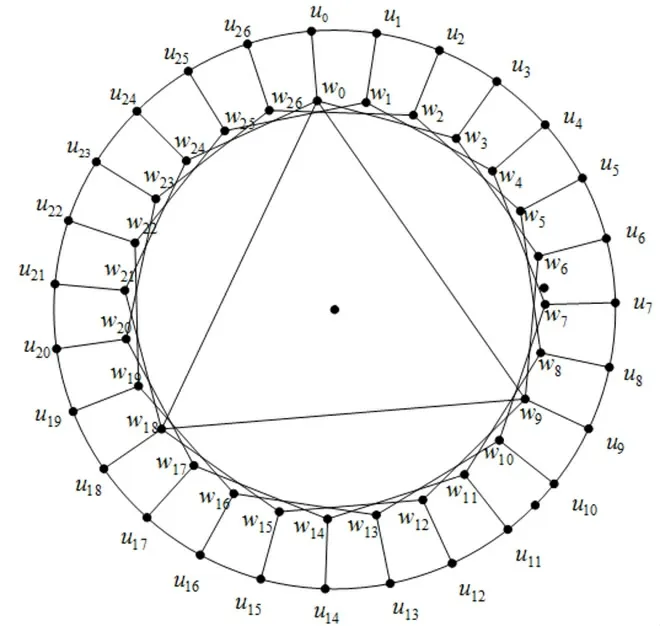
图1 t=3 时的互联网络EGP(33,32,3)

此时EGP(33,32,3)的三个圈U,W,T(如图2所示)具体为

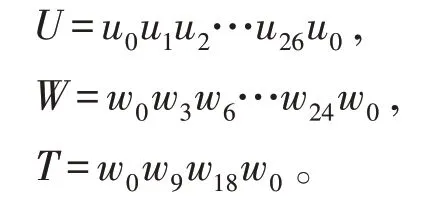
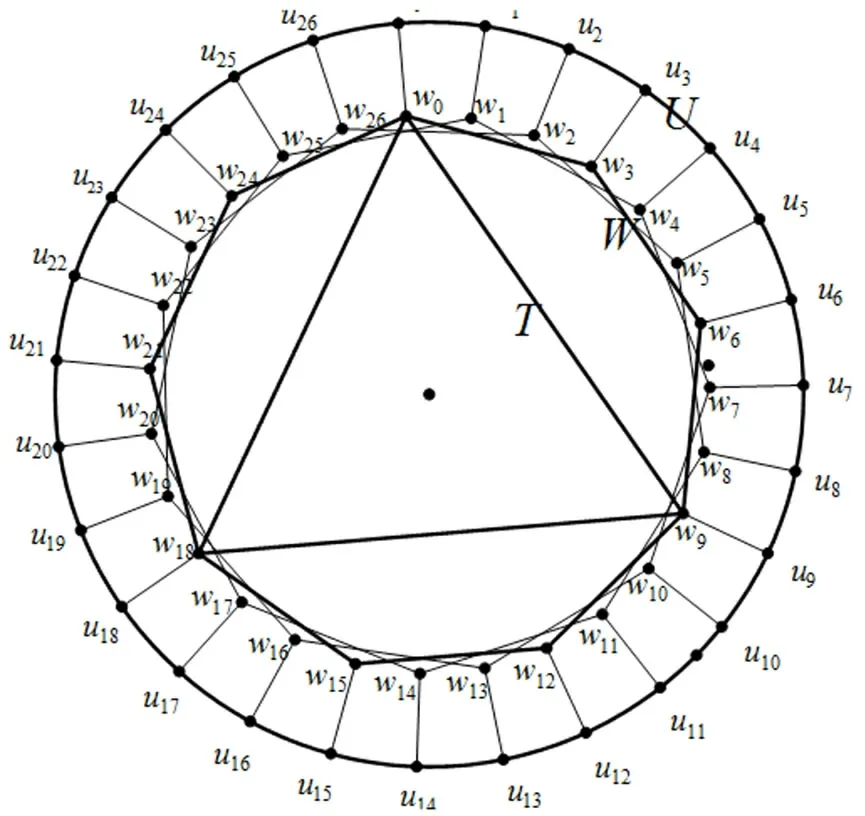
图2 EGP(33,32,3)中的三个圈U, W, T

引理1设v∈V(EGP(t3,t2,t))，则有d(v,U)≤1。

引理2设v∈V(U)=，

则有d(v,W)≤1+t/2。

证明对任意，不妨设v=ukt+r(0≤k≤t2-1,0≤r≤t-1)。

（1）若r≤t/2，取(ukt-ukt+r)路，

P=uktukt+1ukt+2…ukt+r，

则d(v,ukt)≤t/2，可得

d(v,W)≤d(v,ukt)+d(ukt,wkt)≤t/2+1。

（2）若r＞t/2，取(ukt+r-u(k+1)t-1)路，

P=ukt+rukt+r+1ukt+r+2…u(k+1)t，

则d(v,u(k+1)t)≤t/2，可得

d(v,W)≤d(v,u(k+1)t)+d(u(k+1)t,w(k+1)t)≤t/2+1，

综上得证。

引理3设v∈V(W)=，则有d(v,T)≤t/2。

证明对任意v∈，不妨设v=(0≤k≤t-1,0≤r≤t-1)。

（1）若r≤t/2，取路，

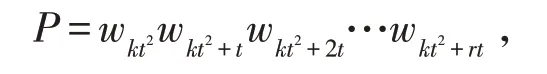
（2）若r＞t/2，取路，

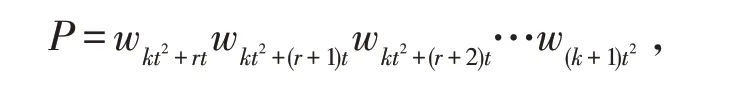
综上得证。

引理4设u,v∈V(T)=，则有d(u,v)≤t/2。

证明对任意

不妨设

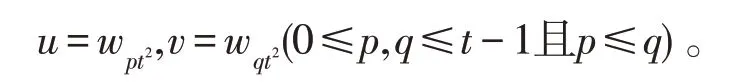
（1）若q-p≤t/2，取路，

则d(u,v)≤q-p≤t/2。

（2）若q-p＞t/2，取路，

则d(u,v)≤[(t-1)-q]+(p+1)=t-(q-p)＜t/2，综上得证。

定理1对于任意不小于3 的正整数t，EGP(t3,t2,t)网络的直径

diam(EGP(t3,t2,t))=+4。

证明对任意u,v∈V(EGP(t3,t2,t))，根据引理1，2，3，4可有

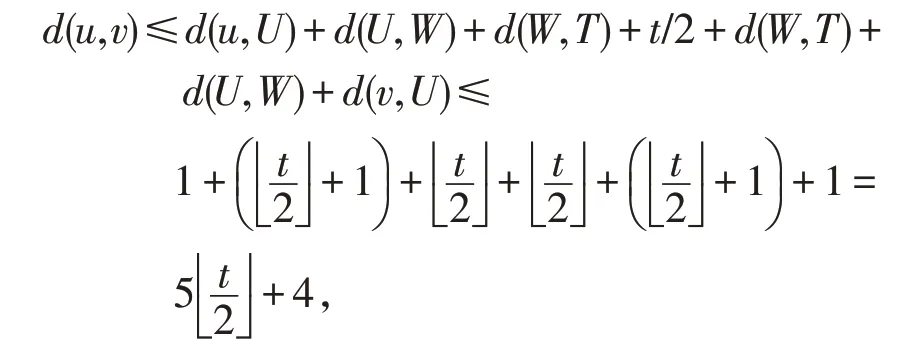
故EGP(t3,t2,t)网络的直径

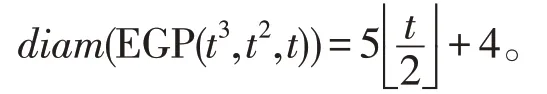
综上可有

通过表1，可以看到，EGP(k3,k2,k)网络与RPC(k)网络和RP(k)网络的性能比较，连接度是相同的，但网络直径更小，优于文献[5]中的RP(n)网络的直径，也优于[6]中的RPC(k)网络的直径。

表1 EGP(k3, k2, k)网络与RPC(k)和RP(k)的性能比较

3 结论

在广义Petersen 图的基础上进行扩展，通过对广义Petersen 图的重构形成了EGP(k3,k2,k)网络。与其它基于Petersen图构造的并行计算机互联网络(如RPC(k)网络和RP(k)网络)相比，EGP(k3,k2,k)网络具有高度近正则性和小直径特点，特别是网络直径方面，阶为，优于RPC(k)网络和RP(k)网络的O(n)阶网络直径值，表明构造的EGP(k3,k2,k)互联网络具有更好的通信性能。