悬挂式单轨列车通过曲线段的动力性能

杨泽钰 蔡成标 凌亮 何庆烈 徐翔

（西南交通大学牵引动力国家重点实验室，成都 610031）

悬挂式单轨交通系统是我国近年来新引入的一种城市轨道交通系统。目前，国内对悬挂式单轨交通系统的研究仍处于探索阶段。文献［1］分别对直线梁和曲线梁进行了结构优化设计。文献［2］提出一种30 m双线简支梁的悬挂式单轨桥梁结构形式。文献［3］基于准零刚度理论，利用多体动力学理论优化了悬挂式单轨车辆的垂向隔振性能。文献［4-5］结合现场试验，探究了悬挂式单轨车辆平稳性的敏感影响参数并对单轨车辆的二系悬挂参数进行了优化设计。文献［6］通过试验和理论分析，建立了悬挂式单轨车-桥耦合动力学模型，认为在对悬挂式单轨交通系统进行研究时考虑桥梁为柔性结构非常重要。文献［7-9］采用多刚体动力学软件，建立悬挂式单轨车辆动力学模型，分析了单轨车辆参数对其曲线通过性能的影响。然而，针对悬挂式单轨交通系统曲线段的现有研究尚未结合车-桥耦合动力学理论，忽略了列车通过曲线段时桥梁结构对车桥动力响应的影响。

据此，本文基于多体动力学理论和模态叠加法建立悬挂式单轨交通系统车-桥耦合动力学模型，探究不同曲线半径、跨度和轨道梁布置方式下该系统的动力响应。

1 悬挂式单轨交通系统特点

悬挂式单轨交通系统具有曲线通过性能优异、爬坡性能好等特点。其车辆走行部封闭于下部开口的轨道梁内，车体悬挂于轨道梁下方，与普通轮轨交通系统差异较大。车辆各部件从上到下主要由摇枕、构架、中心销、吊梁和车体组成，其中摇枕通过二系悬挂连接在构架上。悬挂式单轨车辆的走行轮和导向轮均与轨道梁内表面紧密接触，承受车辆整体的荷载并起到牵引制动和导向作用。悬挂式单轨交通系统中的轨道梁和桥墩均为钢结构，其中轨道梁的跨度一般为15 ～30 m。

2 车-桥耦合动力学分析方法

2.1 车辆与桥梁的运动微分方程

依据多刚体理论，建立车辆子系统的运动微分方程［6］

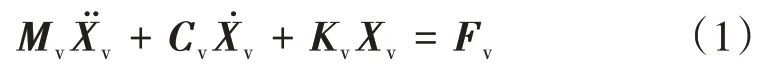
式中：Mv，Cv，Kv分别为车辆子系统的质量矩阵、阻尼矩阵和刚度矩阵分别为车辆的加速度、速度以及位移；Fv为作用在车辆上的所有力，包括结构重力、通过曲线段时引起的离心力、轮胎的法向力和侧偏力等。

采用有限元方法建立桥梁子系统的运动微分方程，并用模态叠加法对其进行解耦。解耦后的桥梁运动微分方程可表示为

式中：qb和ξb分别为桥梁结构的模态坐标向量和模态阻尼矩阵；ωb为由桥梁模态频率组成的对角矩阵；为桥梁结构的振型矩阵；Fb为作用在桥梁上的所有力。

对模态振型进行了质量归一化处理，节点间的振型通过插值求得。

2.2 轮轨相互作用关系

车辆与桥梁之间通过轮轨力联系。悬挂式单轨车辆采用橡胶轮胎，用线性弹簧-阻尼模型模拟，忽略车轮变形对径向刚度的影响。则轮胎径向力Fj可表示为

式中：kj为轮胎径向刚度；cj为轮胎径向阻尼；Δr为轮胎径向压缩量，Δr≤0时轮胎与轨道梁不接触，此时轮胎径向力为0；R和Ṙ分别为轮轨径向相对位移和相对速度；Jw，Jb分别为轮轨接触处车轮径向位移和轨道梁位移；ηb为轨道梁内表面不平顺。

轮胎侧偏力Fy和回正力矩My分别为

式中：ky和k'y分别为轮胎的侧偏刚度和回正刚度；α为轮胎侧偏角，α= arctan(v/u)，v和u分别为轮胎侧向速度与前进速度。

将车辆子系统和桥梁子系统的运动微分方程通过轮轨相互作用关系进行联立，即可得到用于后续计算的悬挂式单轨交通系统车-桥耦合动力学模型。

3 仿真模拟与现场试验验证

3.1 桥梁模型及参数

为验证所建模型的正确性，以四川省悬挂式单轨试验线（图1）为研究对象进行仿真模拟和现场试验。其直线段轨道梁设计跨度为25 m，每隔1.6 m 设置加筋肋，轨道梁横截面尺寸为0.78 m×1.10 m，桥墩高度10.8 m。桥梁有限元模型及截面尺寸见图2，桥梁材料参数见表1。前两阶模态的振型及自振频率见表2。仿真采用的不平顺为现场测得的直线段轨道梁内表面不平顺，见图3。其波长范围为0.5 ～25.0 m，悬挂式单轨列车的运行速度为5 ～60 km/h，不平顺的激励频率小于34 Hz。为保证仿真精度，仿真时采用的桥梁模态振型最高频率为87.6 Hz。

图1 四川省悬挂式单轨试验线

图2 桥梁有限元模型及截面尺寸（单位：mm）

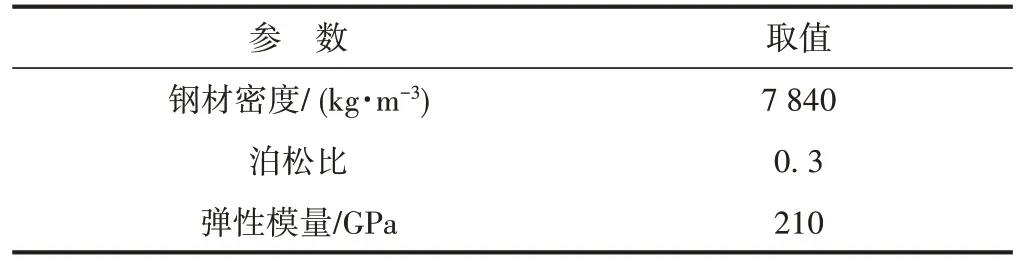
表1 桥梁材料参数

表2 桥梁前两阶模态的振型及自振频率

图3 轨道梁内表面不平顺

3.2 车辆参数

根据实际运营情况，采用2 节车辆的编组形式。车辆计算参数见表3。

表3 车辆计算参数

3.3 模型验证

分析工况为车辆以40 km/h 的速度通过悬挂式单轨试验线直线段。为测量桥梁结构在列车作用下的响应，分别在跨中和墩顶设置免标靶挠度仪及三向加速度传感器，挠度仪精度为0.02 mm，采样频率为117 Hz，加速度传感器量程为50g。参照GB/T 5599—1985《铁道车辆动力学性能评定和试验鉴定规范》，在试验车辆内与构架重心垂向投影间隔1 m 的地板上布置加速度传感器。对测得的车辆加速度采用40 Hz 低通滤波处理，桥梁垂向、横向加速度分别采用20，10 Hz 低通滤波处理。

现场实测值与仿真计算值对比见图4，两者吻合较好，表明本文建立的模型能真实反映实际情况。

图4 现场实测值与仿真计算值对比

4 曲线参数对车桥动力响应的影响

车辆通过曲线时的动力性能与通过直线时有较大差异，必须考虑在曲线上车辆的侧摆、桥梁结构的变形等，但目前尚不明确悬挂式单轨交通系统在曲线段运行性能。因此，采用以上建立的车-桥耦合模型，设置多种曲线工况进行仿真分析，探究曲线参数对车桥动力响应的影响规律。

4.1 单线桥轨道梁布置方式对车桥动力响应的影响

目前试验线均为单线桥，其轨道梁有2 种布置方式，如图5 所示。车辆经过曲线段时桥梁结构受车辆的垂向与横向荷载作用产生变形。2 种布置方式下桥墩受力产生的变形如图6 所示。其中：Fz(t)，Fy(t)分别为桥墩受到的垂向荷载、横向荷载。可以看出车辆经过时2种布置方式下桥墩动态变形有较大差异。

图5 单线桥轨道梁布置方式

图6 桥墩变形示意

设置曲线段桥梁跨度为25 m，曲线半径分别为150，200，250，300 m，列车侧向通过速度为40 km/h，分析列车通过不同轨道梁布置方式的单线桥时车桥动力响应。由于未获得曲线段悬挂式单轨交通系统实测不平顺数据，因此仿真计算时不考虑不平顺的影响。车辆和桥梁结构的动力响应结果见表4、表5，表中的曲线内侧和曲线外侧表示不同轨道梁布置方式。

表4 车辆横向动力响应

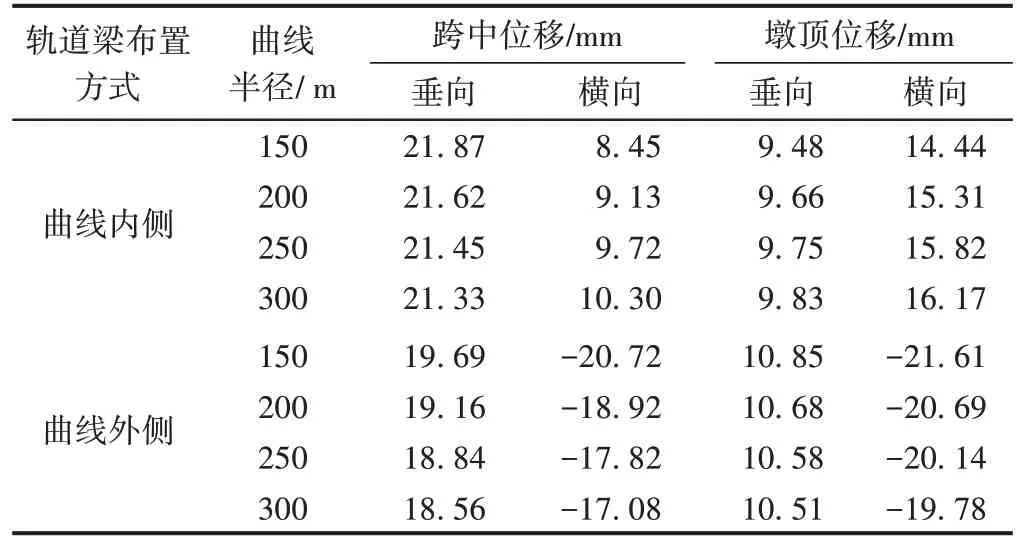
表5 桥梁动力响应

由表4、表5可知：

1）单线桥轨道梁不同布置方式对车体横向加速度影响不显著，但对车体横向位移影响明显。轨道梁布置在曲线外侧时，车体横向位移绝对值较布置在曲线内侧时平均增加约10.38 mm。设计单线桥曲线段时，应将轨道梁布置在曲线内侧以减小车辆的横向位移。

2）曲线半径为150 m 时，轨道梁布置在曲线内侧时跨中横向位移为8.45 mm，而轨道梁在曲线外侧时跨中横向位移达到20.72 mm。这是由于轨道梁布置在曲线内侧时横向弯曲方向与朝向相同，跨中横向位移与桥墩横向位移存在相互抑制关系。因此轨道梁宜布置于曲线内侧，同时降低车辆及桥梁结构的横向位移。

4.2 曲线半径和跨度对车桥动力响应的影响

采用轨道梁布置于曲线内侧的模型，研究不同曲线半径和跨度时车桥的动力响应。曲线半径分别取150，200，250，300 m，跨度参照DBJ51/T099—2018《悬挂式单轨交通设计标准》［10］，分别取15，20，25，30 m，列车侧向通过速度为40 km/h。不同工况下车桥动力响应见图7、图8。

图7 不同曲线半径和跨度时车辆横向动力响应

由图7 可以看出，通过曲线时车辆横向动力响应同时受曲线半径和跨度影响。导向轮径向力随曲线半径增大而减小，随跨度增大而增大，车辆通过较小半径曲线时所受的离心力较大，导向轮为起到有效导向作用需提供更大的径向力。车体横向加速度最大值与横向位移绝对值均随曲线半径增大而减小。

由图8 可以看出，桥梁结构的垂向位移主要受跨度影响。轨道梁跨中与墩顶垂向位移均随跨度增大而增大，而曲线半径对其影响不显著。跨中横向位移受跨度和曲线半径影响，其随跨度增大而增大，同时轨道梁为柔性结构，受车辆离心作用产生的导向轮径向力可抑制轨道梁受车辆重力作用产生的横向变形，因此轨道梁跨中横向位移随曲线半径增大而增大。

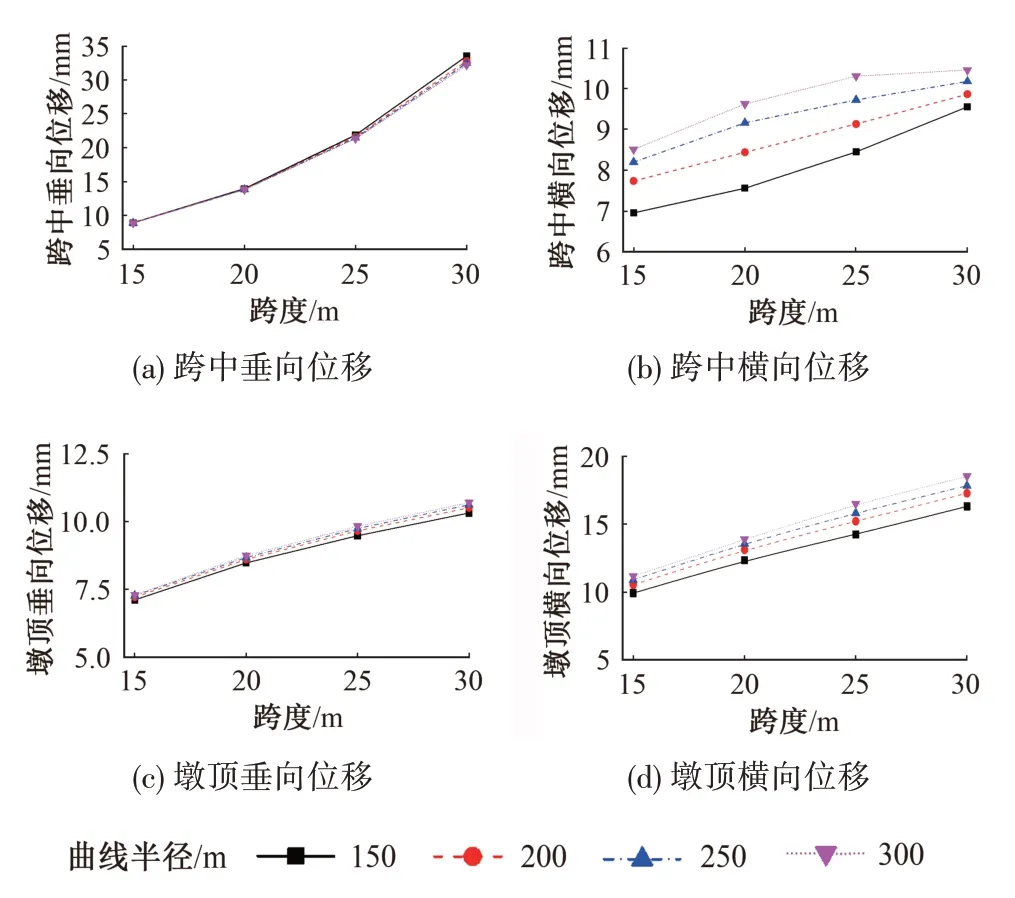
图8 不同曲线半径和跨度时桥梁动力响应

曲线段桥梁跨度为15 m 时，车辆和桥梁的横向动力响应均较小。小半径曲线段桥梁跨度宜为15 m。

5 结 论

本文建立了悬挂式单轨交通系统车桥耦合动力学模型，分析了车辆通过曲线时，不同轨道梁布置方式、曲线半径和跨度对车桥动力响应的影响规律。主要结论如下：

1）不同轨道梁布置方式对车桥动力响应影响显著。单线桥曲线段轨道梁宜布置于曲线内侧，可同时降低车辆及桥梁结构的横向位移。

2）列车通过曲线时，导向轮径向力可抑制轨道梁因受车辆重力作用产生的横向变形，桥梁跨中横向位移随跨度和曲线半径增大而增大。

3）考虑减小车辆与桥梁结构的横向位移，悬挂式单轨交通系统小半径曲线段桥梁跨度宜为15 m。