地铁不同曲线半径下钢轨磨耗发展特性

2020-11-07王志强雷震宇

铁道建筑 2020年10期

王志强雷震宇

（同济大学铁道与城市轨道交通研究院，上海 201804）

随着城市轨道交通向高速度、高密度趋势发展，轮轨间的磨耗问题日益加剧，严重影响列车运营的稳定性和安全性，甚至可能引发车辆轮对脱轨事故［1-2］。包含在车辆-轨道系统中的变量均会对钢轨磨耗产生影响，其中线路曲线半径的影响尤为明显。不同曲线半径会造成钢轨型面不同程度的侧磨，小半径曲线的外轨侧磨现象尤为严重，大量曲线线路外轨由于侧磨超限而报废。

研究地铁不同曲线半径下的钢轨磨耗特征，掌握磨耗发展规律，对于钢轨的养护维修具有一定的指导意义。对钢轨磨耗的研究主要有现场实测数据分析和数值仿真2种手段。现场实测数据能够精确地反映钢轨磨耗的实际情况；数值仿真可以具体分析磨耗的原因及影响因素，弥补现场试验只能从磨耗结果分析的缺陷。

娄平等［3］通过对25 条铁路曲线外股不同轨种钢轨侧面磨耗的实测数据进行分析，得到钢轨侧面磨耗值与累计通过总重的规律。周宇等［4］对上海地铁1 号线、8 号线的典型小半径曲线钢轨磨耗进行了跟踪测量，统计分析小半径曲线钢轨的侧磨和垂磨特征及相应的磨耗发展率。颜怡翥［5］对广州地铁5 号线小半径曲线钢轨磨耗情况进行了现场调查，分析钢轨磨耗加快的原因，认为改进涂油方式是减少钢轨磨耗的有效措施。潘建杰等［6］统计了北京地铁弯道线路上的钢轨侧磨类型，分析了磨耗的主要原因并提出了减缓磨耗的措施。孙宇等［7］基于 Kalker 非 Hertz 滚动接触理论和Braghin磨耗模型，建立了可以考虑磨耗沿钢轨纵向和横向的三维分布的磨耗计算模型，并利用该模型对无砟轨道直线段钢轨磨耗的演变状态进行了计算分析。

上述研究侧重分析某一种曲线半径情况下的钢轨磨耗问题，鲜有关于不同曲线半径下钢轨磨耗的分布发展特性的研究。本文建立了地铁车辆-轨道耦合动力学模型并对模型进行了验证，利用Archard 模型计算不同曲线半径线路钢轨的磨耗范围和程度，研究钢轨型面的磨耗特性及钢轨磨耗与曲线半径的关系。

1 车辆-轨道耦合模型

1.1 车辆模型

采用多体动力学软件UM 建立地铁车辆模型，包括车辆、转向架、轮对。车体和转向架为刚体；轮对为柔性体，具有质量和转动惯量。车体与转向架之间的二系弹簧、转向架与轮对之间的一系弹簧均通过弹簧阻尼单元进行模拟，具有3 个方向上的刚度和阻尼。车辆模型各参数取值参考文献［8］。

1.2 轨道模型

采用柔性轨道模型。钢轨采用考虑剪切变形的Timoshenko梁进行模拟；扣件采用Bushing力元进行模拟，考虑3 个方向的刚度和阻尼。轨道结构各参数取值参考文献［8］。

1.3 轮轨接触模型

轮轨接触模型采用Kik-Piotrowski 计算模型，假设沿车轮滚动方向的轮轨法向接触应力呈半椭圆分布。接触区域根据轮轨之间的虚拟穿透原理得到；法向接触应力由接触区域的几何点满足接触条件求得；切向接触问题通过改进的FASTSIM算法解决［9］。

车辆-轨道耦合模型如图1所示。

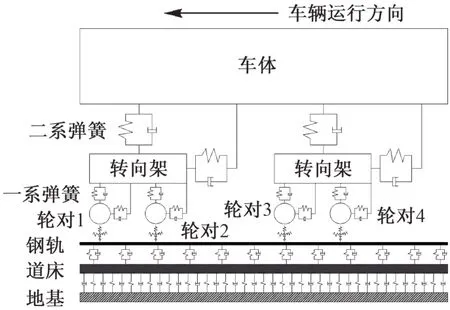
图1 车辆-轨道耦合模型

2 磨耗模型

采用Archard 磨耗模型计算钢轨材料的磨损。该模型可以考虑轮轨间法向应力过大以及不同滑动速度对磨耗系数的影响，对磨耗系数取值的考虑更为全面细致［10］。Archard磨耗模型的计算公式为

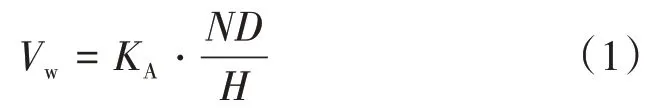
式中：Vw为磨耗体积，m3；KA为磨耗系数；N为法向力，N；D为滑动距离，m；H为材料硬度指数，取值与轮轨材质、滑动速度和接触压应力有关［11］，N/m2。

由式（1）可知：钢轨材料的磨耗体积随着法向力和滑动距离的增大而增大，这与实际线路上钢轨轨距角附近磨耗较为严重的现象相吻合；钢轨材料的磨耗体积随着材料硬度的增大而逐渐减小，这与实测钢轨磨耗随着钢轨硬度的增大而减小的现象相吻合。因此，Archard磨耗模型能够较好地用于钢轨型面侧磨和垂磨的计算。

把轮轨接触斑分为若干个矩形单元，则任一矩形单元中心的磨耗深度Δz为

式中：p(x，y)为法向应力分布；Δd为任一单元格的滑动量。

综合应用式（1）、式（2），即可进行钢轨型面磨耗的计算。

3 模型验证

选取一地地铁上行小半径曲线段外轨进行实测，取直缓点、缓圆点、曲中点、圆缓点、缓直点5 大测点。测量周期为新轨上道至地铁运营，共4 个月（120 d），期间未进行钢轨打磨。

该线路为半径350 m的小半径曲线，长218.063 m，曲线超高120 mm，轨底坡1/30。扣件为DTVI2型，轨下基础为整体道床。列车为6 节编组，测试期间每日运行530余次。采用钢轨轨头廓形测量仪对钢轨测点进行测量，并使用配套的钢轨磨耗测量分析系统对钢轨轮廓进行计算处理。

以曲中点测点为例，测量周期内通过的车轮次数约1.5×106次。基于车辆-轨道耦合模型和Archard 磨耗模型，将车辆4 个车轮引起的磨耗深度和范围分别叠加到钢轨型面上，得到钢轨磨耗型面图。模型中车速选用与实际线路运营速度相近的60 km/h。以钢轨最大磨耗深度0.100 mm 作为型面输出的间隔［12］，并对磨耗后的钢轨型面进行平滑处理。数值模拟计算得到的钢轨磨耗仿真型面与实测型面对比见图2。

图2 钢轨仿真型面与实测型面对比

由图2可知：实测型面磨耗最大值为0.694 mm，平均值为0.202 mm；仿真型面磨耗最大值为0.696 mm，平均值为0.210 mm。模型的误差很小，磨耗最大值和平均值误差分别为0.2%和4.0%。因此，所建模型可靠。

4 钢轨型面磨耗特性

运用车辆-轨道耦合模型和Archard 磨耗模型，基于实测线路情况，施加德国低干扰不平顺谱，取型面输出次数为20 次，以钢轨最大磨耗深度0.100 mm 作为型面输出的间隔［12］，并对磨耗后型面进行平滑处理。通过数值模拟计算得出不同曲线半径（R= 350，450，550，650，750，850 m）下钢轨的磨耗特性。

各曲线半径下的钢轨累计磨耗见图3、图4。

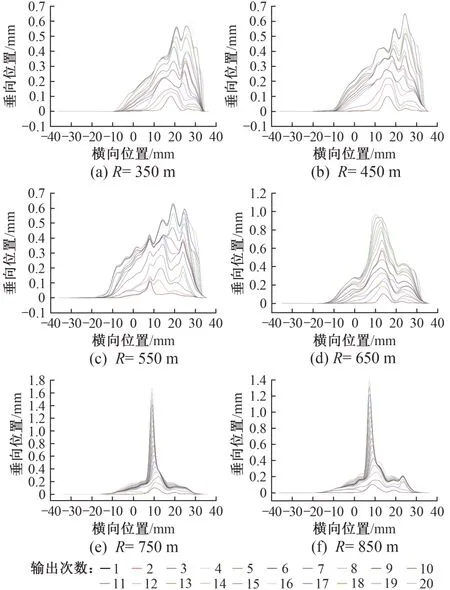
图3 各曲线半径下外轨累计磨耗

图4 各曲线半径下内轨累计磨耗

由图3、图4 可知：①外轨磨耗主要分布于轨头中部和轨肩区域（钢轨横向位置x=-17.5 ～35.0 mm），其中x= 5.0～32.5 mm 的轨肩区域磨耗量较大；内轨磨耗主要分布于轨头中部区域（x= -10.0 ～15.0 mm），其中x= -7.5～12.5 mm 区域的磨耗量较大。②内外轨磨耗分布范围均随着曲线半径的增大而减小，说明曲线半径越大钢轨磨耗范围越集中。③在相同的型面输出次数下，外轨磨耗峰值均大于内轨，且外轨倾向于发生侧面磨耗，内轨主要发生轨顶磨耗。