基于灰色区间理论的重载铁路轨道质量指数发展预测

2020-11-07赖思成高建敏閤鑫

铁道建筑 2020年10期

赖思成高建敏閤鑫

（西南交通大学牵引动力国家重点实验室，成都 610031）

重载铁路由于其大轴重、大运量等特点，使得轮轨动态作用力更大，轨道平顺状态的恶化速度更快，这对重载铁路的养护维修工作提出了更高要求。如何及时跟踪轨道状态的变化规律，科学判定轨道状态，是轨道养护维修中的重要问题［1］。曲建军［2］采用PWMIS 系统中的线路维修捣固预测模型对轨道质量指数（Track Quality Index，TQI）的发展规律进行了预测。Guler［3］建立了人工神经网络模型对轨道几何状态恶化进行了预测。许玉德等［4］利用线性预测模型对轨道质量指数变化情况进行了预测。常欢等［5］提出了改进的轨道质量指数线性预测模型。朱芳草等［6］建立了灰色理论模型预测轨道质量指数的变化情况。

尽管许多学者对多种预测方法进行了探讨，但是，这些方法是否适合于重载铁路轨道不平顺检测数据，还有待进一步分析。TQI值时间序列具有小样本振荡特点，而灰色区间预测模型对小样本振荡序列能较好模拟及预测，因此本文参考国内外相关研究，基于灰色区间预测方法中的包络带预测法［7］，建立重载铁路TQI 的灰色区间预测模型，对我国一重载铁路实际检测数据进行分析，验证预测模型的适用性，以期为我国重载铁路轨道质量状态的评估和养护维修提供参考。

1 重载铁路TQI实际数据分析

根据一重载铁路连续1 年现场实测数据，分析了重载铁路TQI的变化情况，掌握数据的一般规律，为预测分析奠定基础。

1.1 TQI值累积频率分布

以该重载铁路上行K000—K582 段2018 年1—12 月检测数据为样本，计算得到该区段34 183 个TQI值。TQI值频率分布直方图与累积频率分布见图1。可以看出，该重载线路2018 年TQI值大部分介于4～12 mm，其中处于5.5～6.0 mm 区间的里程段最多，处于6.0～6.5 mm 区间的里程段次之。TQI值频率直方图近似呈正态分布；而TQI值累积频率曲线较陡，且TQI值小于12 mm 的里程段占总里程段的95.665%，说明该重载铁路线路整体状态较好。

图1 实测TQI值频率直方图和累积频率分布

1.2 TQI超限与均值统计

《铁路线路修理规则》［8］中规定的TQI管理值见表1。

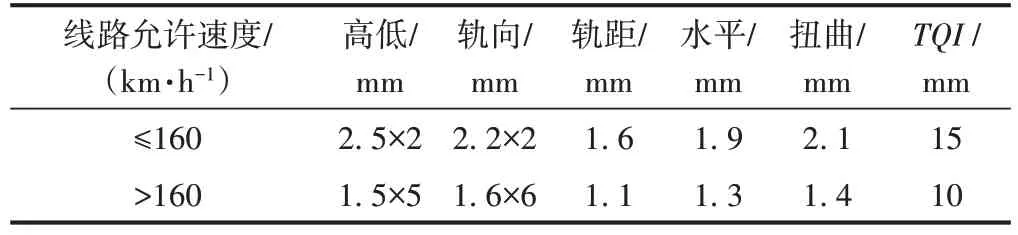
表1 TQI管理值

该重载铁路线路的设计时速不超过120 km/h，参考表1，该重载铁路TQI管理值应为15 mm。从有效轨检数据计算结果来看，TQI＜15 mm 的里程占总里程的99.131%。此值偏大，不利于行车安全，而TQI＜12 mm的里程占总里程的95.665%，故本文根据3σ原则［9］，将该重载线路的TQI管理值初步定为12 mm。

2018 年该重载铁路线路每月TQI平均值与超限率见图2。可以看出，该重载铁路TQI平均值与超限率变化趋势相似。2018 年1 月—9 月TQI平均值与超限率均在缓慢增加，即使有小幅波动，变化也不大；9 月—10 月数值急剧减小，这是因为9 月—10 月重载铁路全线在进行养护维修。

图2 实际TQI平均值与超限率变化曲线

由于维修后列车运行初期轨道不平顺幅值变化很快，不能代表一个维修周期内不平顺变化速率，所以，应根据线路设备实际情况选择每一个周期，从维修结束后下一个相对稳定的检测时间节点开始至下一次维修之前。本文选1 月—9 月的数据进行分析。该重载铁路TQI值时间序列数据具有小样本波动增长的特点，因此采用灰色区间预测模型对其进行模拟预测。

2 灰色区间预测模型

各种时间序列分析方法都得保证序列时间间隔相等。为便于分析计算，须先将TQI值非等时距序列转化为等时距序列，再建立灰色区间预测模型。

2.1 分段三次Hermite插值的等时距转换

由于每月TQI 检测的时间不固定，时间间隔并不完全相同。若直接将原始TQI值时间序列划分为上下界序列，建立非等间距GM（1，1）模型进行区间预测计算，则序列时间跨度约365 d，时间响应函数计算次数非常多，复杂费时。为提高计算效率，遇到时间跨度大的问题时可先采用分段三次Hermite 插值对原始序列进行等时距转换，再将等时距序列划分为上下界序列，建立非等间距GM（1，1）模型进行区间预测计算。

2.2 TQI的灰色区间预测模型

等时距序列

的上缘点构成的序列为上界序列

的下缘点构成的序列为下界序列

对上下界序列分别建立非等间距GM（1，1）模型，设等时距TQI值序列为非等间距GM（1，1）模型的原始数据，则时间间距序列：Δt={Δt1，Δt2，…，Δtn}。其中Δt1= 1，Δtk=tk-tk-1，k= 2，3，…，n。一阶累加序列其中，的紧邻均值序列其中

非等间距GM（1，1）模型的基本形式为

式中：a为发展灰度；b为内生控制灰数。

采用最小二乘法估计a和b，得

则时间响应函数为

可得非等间距GM（1，1）模型的解为

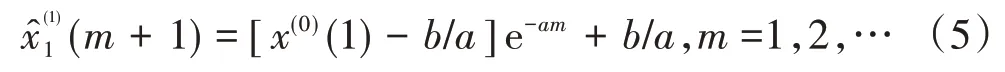
则可得原始数据的拟合值为

利用此方法可分别计算得出TQI值上界序列的预测值为下界序列的预测值为则该重载铁路单元区段TQI值时间序列的基本预测值为

2.3 模型精度检验

为判定模型是否合理，可通过计算上下界序列的预测误差和平均相对误差来评估模型的精度等级。精度等级划分见表 2［10］。

表2 精度等级划分与模型评价

3 算例分析

3.1 区段TQI平均值的预测

重载铁路线路K494+200—K496+400 区段情况稳定，检修数据良好。以该区段2018年1月—8月的TQI值序列为原始数据建立预测模型，预测该区段2018年9月的TQI平均值。

取该区段同一次检测数据算得TQI平均值，见表3。将其作为观测值。

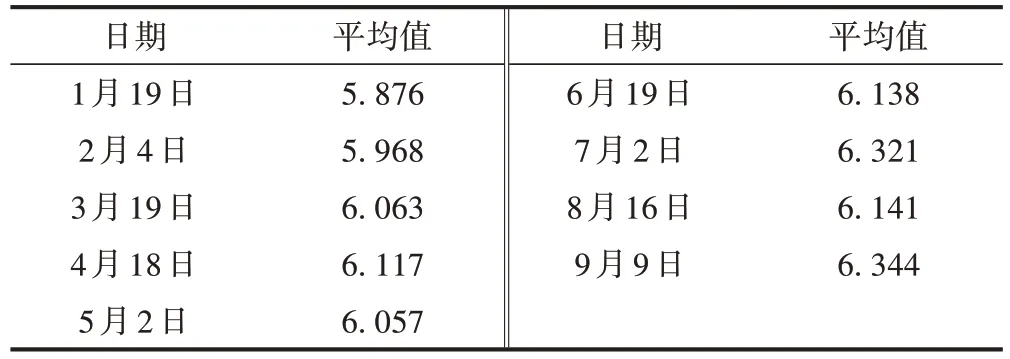
表3 K494+200—K496+400区段TQI平均值 mm

K494+200—K496+400 区段均值序列经过分段三次Hermite 插值转换为等时距序列，即6.005，6.062，6.117，6.060，6.118，6.300，6.173｝。

根据上下限划分法［11］，划分TQI值的上界序列为

下界序列为

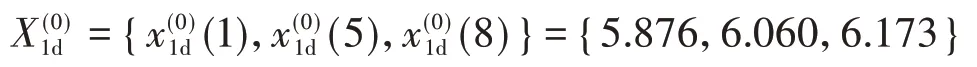
上界序列的时间响应式为

下界序列的时间响应式为

运用灰色区间预测模型对2018 年1 月—8 月的TQI值上下界序列进行拟合，并与经典GM（1，1）模型所得结果对比，见表4。其中，相对误差=∣实测值-拟合值∣/实测值。

表4 2种模型对2018年TQI值的拟合结果对比

从表4 可以看出：灰色区间预测模型对TQI值上下界序列拟合的平均相对误差分别为0.004 178 和0.000 02，上下界序列拟合的精度均为一级；相比经典GM（1，1）模型，灰色区间预测模型的拟合值更接近实测值，相对误差更小，说明灰色区间预测模型对小样本振荡序列具有更好的预测精度。

运用灰色区间预测模型对2018年9月的TQI值进行预测。

上界序列的预测值为

下界序列的预测值为

基本预测值为

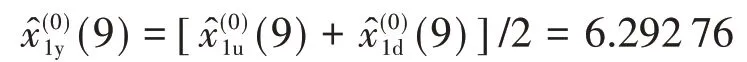
2018 年 9 月 K494+200—K496+400 区段TQI实测值为6.344 mm，在预测区间［6.238 40，6.347 12］内基本预测值为6.292 76 mm，与实测值的相对误差为0.008 08，预测精度为一级，能较好预测TQI值的变化。

3.2 各单元区段TQI值预测

根据TQI平均值的预测值反算求得各单元区段的TQI值，并与实际数据对比以验证预测模型的准确性和有效性。

K494+200—K496+400 区段从小里程端开始每200 m 划分为 1 个单元区段，共划分 12 个。根据 9 月TQI预测值，结合前8 个月各单元区段的TQI数据，可估算9月各单元区段的TQI值，以验证模型的可靠性。

计算各单元区段TQI值比例

9月各单元区段TQI预测值a9n=Mcn，计算结果见表5。可以看出，通过该方法预测的2018 年9 月K494+200—K496+400 各单元区段TQI值与实测值的相对误差较小，预测精度较高，验证了所选数据可靠，所建模型比较准确。

表5 9月各单元区段TQI值预测结果

对于重载铁路线路TQI数据，也可对每一单元区段分别建立灰色区间预测模型，但由于整个检测里程TQI数据量庞大，预测计算量将成倍增加。若采用上述计算方法，则能在保证预测精度的前提下极大提高计算效率。

3.3 不同里程典型区段TQI值预测

在该重载铁路上选取5 个典型区段，区段1 到区段 5 的里程分别为 K90+000—K91+000，K162+000—K163+200，K278+200—K279+400，K324+800—K326+000，K591+200—K520+800。采用上述方法预测TQI值，并与实测值进行对比，见表6。可以看出：各区段实测值与预测值的相对误差均较小，本文预测方法对重载铁路典型区段有较高的预测精度，进一步说明本文所建灰色区间预测模型能较好预测重载铁路TQI发展变化情况，具有较好的适用性。