基于小波变换和ARIMA模型的高速铁路轨道不平顺研究

赵隽 李林灿 左自辉 殷勇

（1.中国国家铁路集团有限公司基础设施检测中心，北京 100081；2.中国铁道科学研究院集团有限公司基础设施检测研究所，北京 100081；3.中国铁路上海局集团有限公司运输部，上海 200071）

高速铁路基础设施是列车安全运行的重要保障。我国高速铁路路网复杂，行车密度高，故障影响范围大，对高速铁路基础设施服役状态提出了更高要求。为提升高速铁路基础设施养护维修质量和效率效益，推进“工电供”综合维修生产一体化改革，中国国家铁路集团有限公司于2017 年和2018 年对高速铁路基础设施维修体系进行改革创新，于2019 年发布了《中国铁路总公司关于深化高速铁路综合维修生产一体化改革的指导意见》，在全路范围内推进高速铁路综合维修生产一体化的实施［1］，并在中国铁路沈阳局集团有限公司成立沈阳高铁基础设施段作为试点。

高速铁路基础设施维护管理主要分为检测监测、日常养护、专业修理3 种类型［2-3］。目前我国铁路基础设施检测形成了3层架构：铁路基础设施检测中心、铁路局集团公司综合检测所、检测分析车间。通过构建新体系，确保设备状态安全和运输效率。高速铁路轨道系统作为日常养护维修的重点，其科学管理关系到运输安全及运营成本。多年研究及实践经验表明，轨道几何形位的平顺状态直接影响轮轨作用、车体振动、乘坐舒适性等。国内外轨道几何平顺状态通过轨道质量指数（Track Quality Index，TQI）来衡量，TQI 值也是编制线路养护维修计划的重要依据。

近年来，国内外诸多学者对轨道状态变化规律的预测做了大量研究。曲建军等［4］认为TQI 序列由恶化的趋势成分+围绕趋势的随机波动成分组成，并在此基础上提出了非等间距的灰色模型GM（1，1）对TQI序列进行预测。贾朝龙等［5］将改进的灰色模型GM（1，1）和AR 模型相结合对轨道不平顺状态进行预测。靳鹏伟等［6］提出的马尔可夫残差修正预测模型，在残差灰色模型拟合变化趋势的基础上，再对得到的随机波动大的残差序列进行马尔可夫预测，从而提高预测精度。

在新的高速铁路综合维修生产一体化改革背景下，天窗资源更加宝贵，维修质量及安全性要求更高。运用科学的方法探索周期性、非线性的轨道几何状态变化规律，预测轨道状态发展趋势，对制定高速铁路综合维修计划、充分合理利用天窗资源、促进线路维修从周期修到状态修的转变、保障运输安全都具有重要意义。

1 模型介绍

1.1 小波变换

小波变换（Wavelet Transform）以窗口化傅里叶变换为基础，相对于傅里叶变换，小波变换可以进行多尺度变换，对时间序列进行局部化分析，将高、低频序列分开分析，保留原序列特征并且突出细节特点，广泛应用于信号和图像处理领域。

函数s(t)的连续小波变换WS(a，b)为

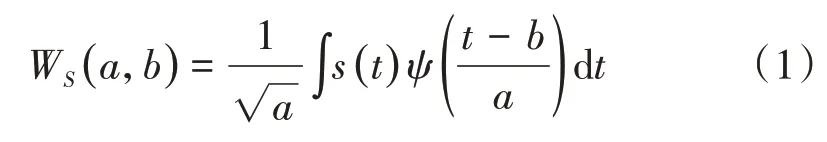
式中：a为小波基函数ψ(t)进行伸缩的尺度参数；b为平移参数。

本研究样本数据是离散型的，因此需要采用离散小波变换。在s(t)的连续小波变换中令a= 2-r，b=2-rk，其中r，k∈ Z，可以得 到s(t) 的离散小波变换WS(r，k)，即

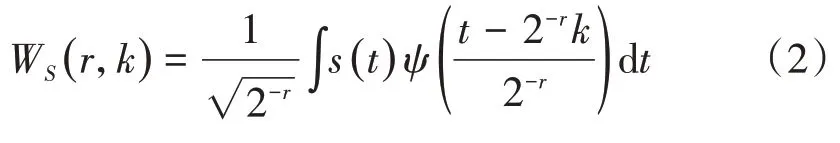
常用的小波基函数主要有Daubechies 小波（db）、Haar 小波、Symlet 小波（sym）等。小波变换主要包含信号分解和重构2个过程。

1）原始信号分解

采用一组高通滤波器H和一组低通滤波器L将原始信号A0分解为高频信号hj和低频信号lj，其中j=0，1，…，J- 1，这里J为分解的最大阶数。细节信息主要存在于高频信号，近似信息主要存在于低频信号。

2）新信号重构

由于每次经过小波分解，信号尺度都变为原来的一半。因此，需要从尺度最小的一层开始，利用L，H的对偶算子L*，H*将分解信号逐层重构，得到每层的重构信号Dj（j=1，2，···，J），则对原始信号的重构信号C为

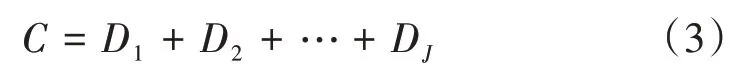
1.2 ARIMA模型

ARIMA 模型全称为自回归移动平均模型（Autoregressive Integrated Moving Average Model），是时间序列分析中的一个重要模型，用于描述依赖于时间的随机变量之间的相关性和延续性［7-8］，广泛应用于经济增长［9］、运量及市场价格变化［10］、人口数量变化等领域。在ARIMA(p，d，q)模型中，AR 为自回归模型，p为自回归项数；MA 为移动平均模型，q为移动平均项数；d为将非平稳序列变为平稳序列所需做的差分阶数。对于非平稳时间序列{Xt}，ARIMA(p，d，q)模型的一般形式为［11］

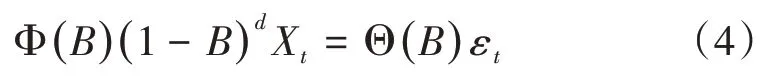
式中：B为差分算子；Φ(B)为模型的自回归系数多项式，Φ(B)= 1-φ1B- ···-φpBp，φp为自回归系数；Θ(B)为模型的移动平均系数多项式，Θ(B)= 1-θ1B-···-θqBq，θq为移动平均系数；εt为零均值白噪声序列。

轨道状态会随着时间发生变化，因此一定时间段内TQI 值可以看作一组时间序列。传统ARIMA 模型对时间序列的分析具有一定预测效果，但预测精度不高，需要不断地通过残差修正才能提高预测精度，增加了计算量和复杂程度，而且每次残差修正还会剔除原始数据的细节信息。本文首先利用小波变换，将原始数据分解为保留细节信息的hj和保留原始数据特征的lj，然后分别对hj，lj进行 ARIMA 建模处理得到新的高频信号和低频信号l'j，再进行小波重构。

2 小波分解

2.1 数据选取

选取 2018 年 2 月至 2020 年 1 月期间，检测列车CRH380BJ-0301 在沈阳基础设施维修段管辖的盘营高速铁路下行线K12+600—K12+800 处获取的TQI 检测值A(0)为研究对象，见图1，其中包含71 个检测值。从序列图可以初步判断，A(0)为一组离散信号，整体较为平稳，在样本时间范围内TQI值无较大波动（原因是盘营高速铁路为无砟轨道，结构比有砟轨道稳定）。盘营高速铁路处于东北地区，TQI 值在春季的春融时会发生变化，由图 1 可以看出，2018 年 2 月至 4 月及2019 年2 月至4 月TQI 值有变大趋势。离散程度不大的原始数据也有助于保证模型拟合的精度。为深入分析TQI时间序列，采用小波变换进行降噪滤波处理，以真实反映轨道平顺状态，探究潜在规律。

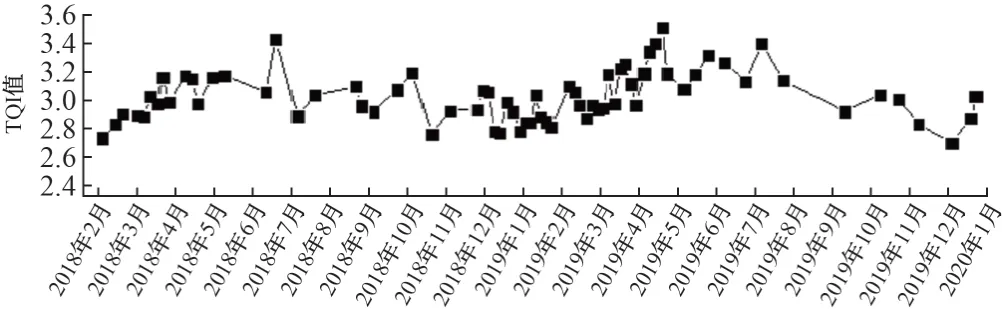
图1 TQI检测值原始序列A0

2.2 TQI序列小波分解

经过反复计算，db6，db7，sym6，sym8 等小波基均适用于本TQI 检测值序列。考虑到数据样本量，选用db7 小波基。将原始序列A(0)进行db7 小波分解，得到高频信号hj和低频信号lj，见图2。可知，高频信号hj在0值附近震荡，较为平稳；低频信号lj也较为平稳。

图2 高、低频信号序列

2.3 高、低频序列处理

利用单位根检验法对高频信号hj、低频信号lj序列进行进一步检验，若存在单位根，则序列不平稳，分析会使序列存在伪回归。对零假设“序列存在单位根”检验发现：原低频信号序列lj存在单位根（概率不为0），序列不平稳；高频信号序列hj不存在单位根（概率为0），序列平稳（表1）。对lj序列进行一阶差分得到序列Δlj，然后利用单位根检验法发现，不存在单位根（表2），表明Δlj序列为平稳序列。

表1 hj单位根检验结果

表2 Δlj单位根检验结果

对小波分解后的高频信号hj和一阶差分后的低频信号Δlj进行分析得到：原始序列A(0)经过小波分解后得到的近似信号lj相对平缓顺滑，趋势更加明显，更便于分析轨道状态变化情况；高频信号hj和一阶差分后的低频信号Δlj满足平稳性，表明轨道状态变化确实存在规律，蕴含不可忽视的信息，可以对其建立时间序列相关模型。

3 ARIMA模型建立

建立ARIMA模型，对经过小波分解后的平稳序列高频信号hj和一阶差分后的低频信号Δlj进行拟合。根据模型的拟合优度检验、残差的白噪声检验、贝叶斯信息准则（BIC），分别确定hjARIMA(p，d，q) 和ΔljARIMA(p，d，q)模型中较优的p，q取值，最后选择最优模型ΔhjARIMA（1，0，1）和ljARIMA（1，1，1）。

以ΔhjARIMA（1，0，1）和ljARIMA（1，1，1）拟合的序列h'j，l'j为新的高频、低频信号，对h'j，l'j进行小波重构，得到拟合值。比较拟合值与实际值（图3）可以看出，拟合的趋势与实际趋势基本一致。模型的平均相对误差、均方根误差分别为0.89%，1.12%，表明模型预测效果良好。

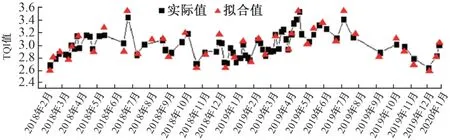
图3 拟合值与实际值比较

4 模型拟合结果分析

根据模型拟合结果，判定轨道不平顺状态是可以进行预测分析的，且小波分解后的高频序列和低频序列均呈现出平稳性，表明轨道不平顺状态是有规律的变化，这也与轨道状态实际变化情况一致。轨道几何平顺状态随着列车动载的反复作用，轨道的轨距、水平、方向、高低、三角坑等几何形位会发生变化，形成轨道不平顺。由于钢轨接头、焊缝、轨枕这些很可能造成TQI 大值点的因素本身就是间隔一定距离布置的，具有间歇效应，因此轨道不平顺状态具有周期性变换的特征［12-13］。

初步分析得到，样本和拟合值中的非平稳序列是轨道几何状态离散不平顺和随机性不平顺的体现。轮轨作用过程中，比较常见的离散不平顺因素包括岔区、钢轨擦伤、钢轨轨缝等，这些因素会造成轨道几何尺寸突变甚至超限，且不能通过函数进行描述或寻找规律，完全是随机的，只能通过日常巡检发现，属于偶然离散不平顺。由于钢轨波长和波幅是随机变量，从极窄时域的角度看轨道几何状态变化本身就是随机的，小波变换本身是将全时域的傅里叶变换窗口化，保留了傅里叶变换平均掉的峰值、突变点等细节信息。

经过小波分解和重构再进行ARIMA 拟合的新序列保留了原序列中的突变信号等随机的信息。若这些随机信息确实是由故障点造成的，仅进行传统的分析预测只能发现轨道几何状态变化大致趋势，这些细节变化的故障点会在数据处理过程中被剔除，对列车运行安全造成隐患。

5 结语

沈阳高速铁路基础设施段作为综合维修改革的试点段，其在新模式下的设备设施维修保养质量都是值得分析研究的。从本文的数据分析来看，所选择样本盘营高速铁路下行线某区段TQI 值存在一定规律；从ARIMA 模型拟合结果来看，预测效果良好。基于小波变换的ARIMA模型，提高了传统分析预测模型的精度和灵敏度，在预测轨道几何状态变化趋势的同时保留了细节信息，可以及时地对发现的故障点进行整改，避免故障检测遗留。本文的研究可以为轨道几何状态研究以及ARIMA 模型的改进提供例据，推动优化高速铁路综合维修计划，提高天窗资源利用效率和运输效率。