铁路40 m跨度混凝土简支箱梁的畸变效应
2020-11-07颜维毅蔺鹏臻
颜维毅 蔺鹏臻
(1.兰州交通大学甘肃省道路桥梁与地下工程重点实验室,兰州 730070;2.兰州交通大学土木工程学院,兰州 730070)
箱梁具有抗扭刚度大、截面效率高、施工方法现代化等特点,与T 梁相比,可缩短工期,节约成本[1],被广泛应用于铁路交通工程建设中[2]。单线列车活载作用于双线铁路箱梁时会偏离箱梁整体纵轴线,竖向偏心荷载作用下,箱梁发生约束扭转变形,导致横截面轮廓形状改变,即畸变[3]。
箱梁畸变分析常用的方法有解析法和数值法2种,近年来国内外学者对箱梁的畸变效应分析理论进行了大量的研究[4-8]。第1 种理论选用腹板和底板之间的夹角描述箱梁变形的基本未知量。张士铎等[9-10]基于板梁框架法的思想,建立了单室梯形箱梁畸变效应分析的基本公式和控制微分方程。第2种理论的基本位移参数为畸变挠度,将畸变的反对称载荷分解为横截面框架刚度抗力和畸变翘曲刚度抗力2 部分,并通过静力法建立畸变控制微分方程。徐勋等[11]对比分析了以畸变角χ和畸变挠度W为位移参数的2 种畸变分析理论,证明了2种理论分析结果的一致性。Hsu等[12]采用了弹性地基梁比拟法分析畸变微分方程,求解箱梁畸变应力,并以此为基础,提出了等效弹性地基梁比拟法。张元海、胡玉茹等[13-14]提出一种与薄壁箱梁约束扭转分析相似的薄壁箱梁畸变效应分析方法,基于势能驻值原理的能量变分法,建立以畸变角为未知量的控制微分方程,并给出其初参数解。王晨光等[15]根据最小势能原理建立了考虑剪切变形的箱梁畸变控制微分方程,提出了相应边界条件,分析了剪切变形对箱梁畸变效应的影响。
我国既有标准简支箱梁常用跨度为24 m和32 m,尽管对标准简支箱梁畸变效应的研究已有不少文献,但是对于大跨度简支箱梁畸变效应的研究较少。本文以40 m 跨度高速铁路双线简支箱梁为研究对象,通过经典解析法与ANSYS有限元法分析其畸变效应,为大跨度简支箱梁的设计提供参考。
1 分析模型
1.1 箱梁基本参数
40 m 跨度预应力混凝土箱梁跨中截面如图1 所示。桥梁设计标准为双线,线间距4.0 m。轨道结构采用有砟轨道,活载纵向采用ZK活载。梁体为C50混凝土,弹性模量E按规范取3.55×104MPa。

图1 箱梁跨中截面(单位:cm)
1.2 荷载施加与畸变荷载分解
对梁施加ZK 活载中的特种活载,按照最不利位置进行加载,如图2所示。
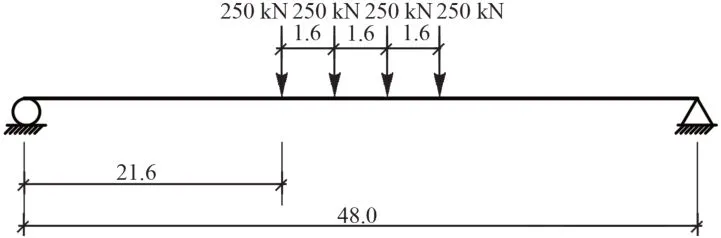
图2 荷载的施加(单位:m)
畸变效应是箱梁空间复合受力中的一种变形模式。箱梁横截面上作用有偏心距e的荷载ΣP(图3(a))。根据截面荷载等效原则[8],将其分为反对称荷载(图3(c))与对称荷载(图3(d))。根据力的平衡原理,反对称荷载又可以分解为刚性周边的纯扭转荷载(图3(e))与自相平衡畸变荷载(图3(f))。
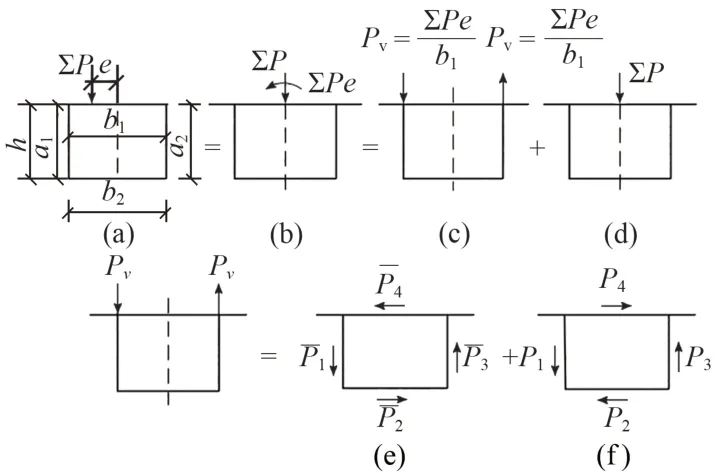
图3 偏心荷载的分解
根据闭口截面自由扭转理论[9],图3(f)中由单个集中力引起的各板的畸变荷载为

根据图1 参数代入式(1)—式(3),得到P1=P3=45.455 kN,P2=P4=80.645 kN。对于双线铁路箱梁,只有当双线列车完全同步行进时才符合对称受力的特点,但是这种完全对称的情况非常少见,绝大多数都会存在偏心活载作用,特别是仅单线列车通过时偏心力矩最大。
2 分析过程
2.1 解析法计算
根据文献[2]将畸变角γ2作为未知量,采用能量变分法进行解析计算。箱梁在畸变荷载作用下的总势能Π可由箱梁横向弯曲的应变能U1、翘曲应变能U2和荷载势能V三部分组成,即

式中:K3,H均为常数,由箱梁的截面几何特性确定。
根据欧拉-拉格朗日条件式,Π取得极值的必要条件为


式中:ID为畸变翘曲惯矩;IR为畸变框架惯矩。
采用弹性地基梁比拟法求解上述微分方程,将其写为
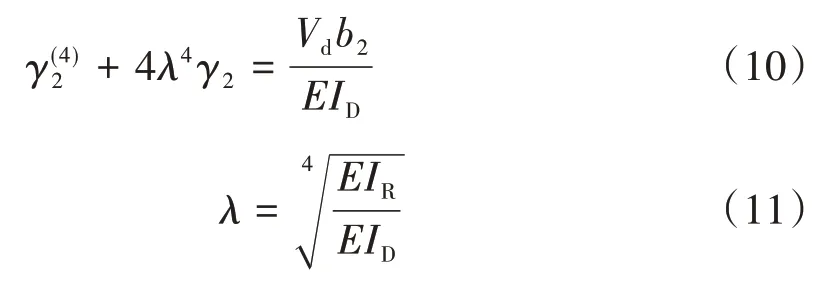
根据边界条件,采用初参数法求解畸变微分方程,可求出γ2。定义畸变双力矩由此求出畸变翘曲应力σdω:

式中:K4为常数,由箱梁的截面几何特性确定。
2.2 ANSYS有限元建模
在ANSYS中采用shell63板壳单元建立模型,边界条件采用简支,对模型施加图3(f)所示的畸变荷载得到畸变翘曲应力。有限元模型如图4所示。为方便观察,选择箱梁截面上畸变效应突出的3 个点作为应力分析控制点:1号点位于右侧腹板与顶板的交界部位;2号点位于右侧腹板与底板的交界部位;3号点位于顶板翼缘板悬臂端部。
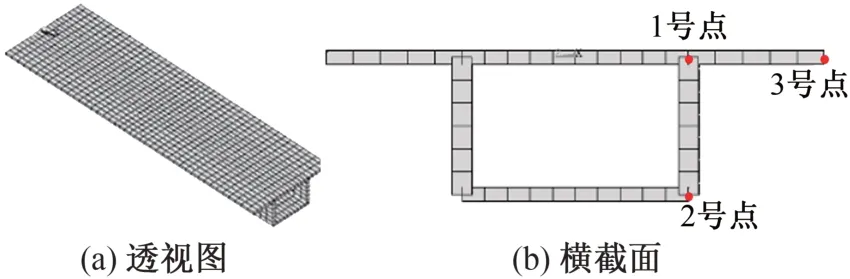
图4 有限元模型
3 计算结果分析
3.1 解析解与有限元解对比
通过对40 m 跨度铁路简支箱梁分别进行解析计算与ANSYS有限元计算,得到跨中截面的畸变翘曲应力分布,见图5。

图5 跨中截面畸变正应力分布(单位:kPa)
由图5可知,解析解与有限元计算值比较接近,但二者存在一些偏差。这是因为ANSYS 板壳有限元可以反映出空间箱梁的真实受力特点,与实际情况较为接近。而在用传统的解析方法进行计算时对实际情况做了简化处理(如忽略了剪切变形等),导致其计算结果有一定的偏差。另外,在箱梁截面上2 号点的畸变翘曲应力最大。
为了分析畸变翘曲应力相对于总应力的变化,取畸变翘曲应力σdω与偏心荷载产生的纵向总应力σx之比ζ进行分析。ζ的表达式为

由上式可知,应力比越大,畸变效应越明显。
3.2 不同跨度箱梁畸变效应对比
保持高跨比不变,使梁的跨度分别等于24,32,40 m,对比跨中截面应力分析控制点的应力比,见表1。

表1 不同跨度箱梁跨中截面应力比
由表 1 可知,与 24,32 m 梁相比,40 m 梁 1 号点和2号点的应力比下降,而3号点的应力比升高。这说明增加简支箱梁的跨度在一定程度上会减弱其畸变效应。
3.3 高跨比对箱梁畸变翘曲应力的影响
选取 40 m 跨度铁路简支箱梁l/2、l/4 和l/8 截面(l为跨度),并对其应力分析控制点进行编号(表2),研究高度h分别为2.5,3.1,3.5,4.0,4.5 m 时(高跨比为0.063,0.078,0.088,0.100,0.113)应力比的变化规律,见图6。
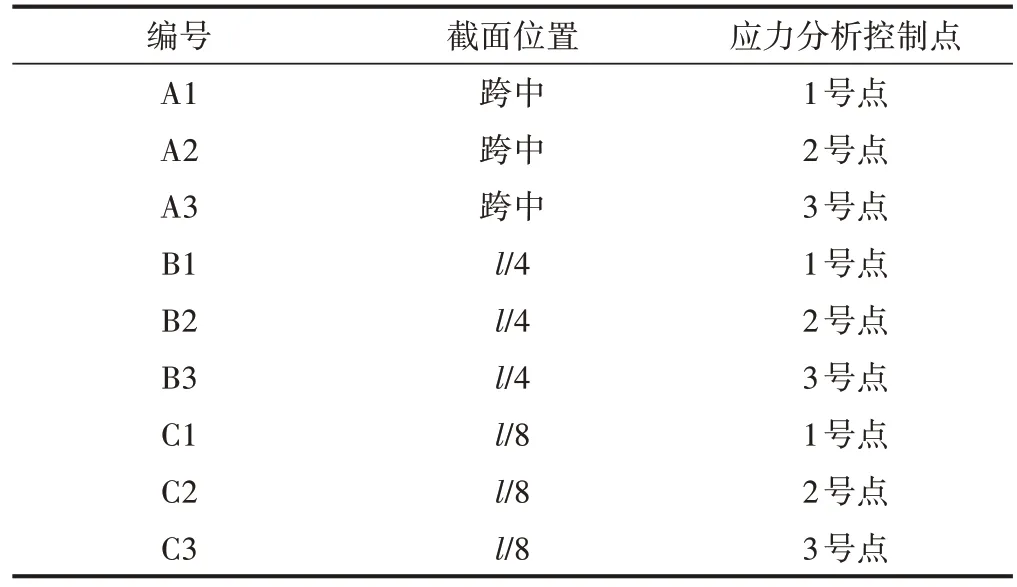
表2 不同截面及应力分析控制点编号
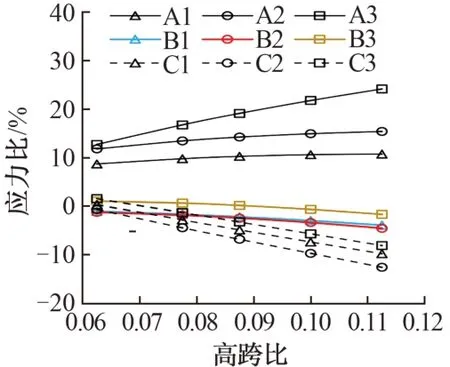
图6 高跨比对畸变效应的影响
由图6可知:
1)随着高跨比的增大,在跨中截面上3 个应力分析控制点的应力比均有增大的趋势,在l/4截面和l/8截面上其应力比均有减小的趋势,说明箱梁越高,跨中畸变效应越明显,且跨中截面应力比始终大于l/4截面和l/8截面。
2)在跨中截面上,3 号点的应力比相对最大,且受高跨比的影响变化最明显。
3)当高跨比为0.088时,跨中截面1号点应力比为10%,2 号点为13%,3 号点最大为17%(不超过20%),说明该截面参数取值较为合理。
3.4 宽跨比对箱梁畸变翘曲应力的影响
研究箱梁宽度b分别为4.5,5.0,5.5,6.0,6.5 m时(宽跨比为0.113,0.125,0.138,0.150,0.163),l/2,l/4和l/8截面上应力比的变化规律,见图7。

图7 宽跨比对畸变效应的影响
由图7 可知:随着宽跨比的增大,3 个应力分析控制点在3个截面上的应力比均有增大的趋势。这说明箱梁越宽,畸变效应越明显;跨中截面应力比始终大于l/4截面和l/8截面。
3.5 壁厚对箱梁畸变翘曲应力的影响
研究壁厚t分别为0.20,0.25,0.30,0.35,0.40 m时l/2,l/4和l/8截面上应力比的变化规律,见图8。
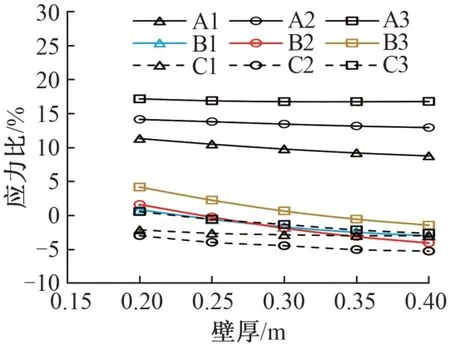
图8 壁厚对畸变效应的影响
由图8 可知:随着顶板和底板壁厚的增大,3 个应力分析控制点在3 个截面上的应力比有减小的趋势,说明增加箱梁壁厚可以在一定程度上减小畸变效应;跨中截面应力比仍大于l/4截面和l/8截面,且3号点的应力比相对最大。
综上可知,随着高跨比、宽跨比和壁厚的增加,3号点的应力比始终最大,此处的畸变效应最明显,在设计中应充分考虑畸变效应的影响。
4 结论
1)解析法与ANSYS 有限元计算出的40 m 跨度简支箱梁的畸变效应接近,板壳有限元可以很好地反映出空间箱梁的真实受力特点。在箱梁发生畸变时,同一截面腹板与底板交点处的畸变翘曲应力最大。
2)随着跨度的增加,简支箱梁的畸变效应有一定的减弱;高跨比和宽跨比的增加会使跨中的畸变效应更加明显,壁厚的增加会使其有减弱的趋势,且跨中截面的畸变效应始终大于l/4截面和l/8截面。
3)对于铁路40 m 混凝土箱梁,腹板与顶板交界处的应力比约为10%,腹板与底板交界处应力比约为13%,顶板悬臂端部应力比最大,约为17%。
