卡尔曼滤波算法的研究与仿真

张波涛 苍鹏浩 刘畅

摘要：卡尔曼滤波算法是卡尔曼和布西于1960年和1961年提出来的一种递推滤波方法，由于系统中状态量受到噪声干扰是随机的不能得到精确数据，卡尔曼滤波是依据一组观测值消除随机干扰，尽可能预测出接近真实值的估计值。它便于计算机编程实现与现场数据实时更新处理，是效率高且最为广泛的滤波方法，在通信、电力、航空等众多工业、军事领域都得到了应用。

关键词：卡尔曼;算法;仿真

滤波本质上是信号处理与变换（去除或减弱不想要的成分，增强所需成分）的过程，这个过程既可以通过硬件来实现，也可以通过软件来实现。卡尔曼滤波属于一种软件滤波方法，基本思想是：以最小均方误差为最佳估计准则，采用信号与噪声的状态空间模型，利用前一时刻的估计值和当前时刻的观测值来更新对状态变量的估计，求出当前时刻的估计值，卡爾曼滤波算法根据建立的系统方程和观测方程对需要处理的信号做出满足最小均方误差的估计，即滤波结果。

1     卡尔曼滤波原理

假设一个离散控制过程的系统满足以下描述：系统的状态转换过程可以描述为一个离散时间的随机过程，系统的状态受控制输入的影响，系统状态及观测过程都不可避免的受到噪声影响，系统状态是非直接可观测的。

该系统可用一个线性随机微分方程来描述，即系统方程：

x（k）=Ax（k-1）+Bu（k-1）+w（k-1）

再加上系统的观测方程：

z（k）=Hx（k）+v（k）

其中：x（k）是k时刻的系统状态，u（k）是k时刻对系统的控制量，w（k），v（k）分别表示过程噪声和测量噪声（假设为高斯白噪声），其协方差分别为Q和R;z（k）是观测值：A是系统状态矩阵;B是系统控制矩阵;H是输出矩阵。

首先我们对系统进行预测，得到预测结果。

利用系统的过程模型，预测下一状态的系统。假设现在的系统状态是k，依据系统的上一状态（即：k-1）和系统模型预测现在的状态：

x（k|k-1）=Ay（k-1|k-1）+Bu（k）      （1）

其中，x（k|k-1）是利用上一状态预测的结果，y（k-1|k-1）是上一状态最优的结果，u（k）为现在状态的控制量，若没有控制量，取值0。

误差的协方差预测方程为：

p（k|k-1）=Ap（k-1|k-1）A+Q     （2）

其中，p（k|k-1）是x（k|k-1）的协方差，p（k-1|k-1）是x（k-1|k-1）的协方差，A是A的转置矩阵，Q是系统噪声的协方差。

然后我们收集现在状态的观测值，结合上述的预测结果，可以得到现在状态（k）的最优化估算值y（k|k）：

y（k|k）=x（k|k-1）+Kg（k）（z（k）-Hx（k|k-1））（3）

其中，Kg为卡尔曼增益，卡尔曼增益方程为：

Kg（k）=p（k|k-1）H/（Hp（k|k-1）H+R）      （4）

为了卡尔曼滤波算法可以递推下去，还需要更新现在状态（即k）下Y（k|k）的协方差：

p（k|k）=（I-Kg（k）H）p（k|k-1）（5）

其中，I为单位矩阵，对于单模型单测量，I=1。

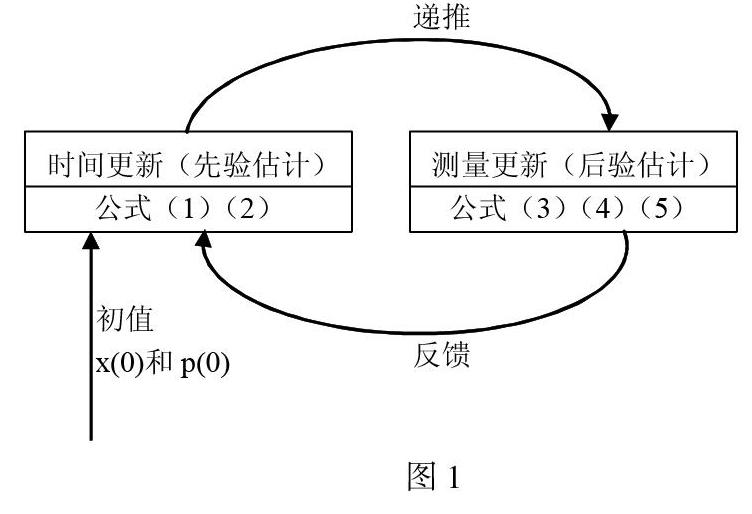
卡尔曼滤波算法本质上是一个递推反馈算法，它的两部分：时间更新方程（状态方程）和测量状态更新方程。其中，前者负责递推，后者负责反馈，将先验估计和新的测量变量结合，以构造改进后的后验估计。为了更直观理解卡尔曼滤波，给出卡尔曼滤波流程图如图1 所示。依据流程图，只要给定初值x（0）和p（0），根据k时刻的测量值z（k）就可以通过递推计算得到时刻的状态估计x（k）。

2     建立数学模型

卡尔曼滤波作为一种数值估计优化方法，与应用领域的背景结合性很强。因此在应用卡尔曼滤波解决实际问题时，重要的不仅仅是算法的实现与优化问题，更重要的是利用获取的领域知识对被认识系统进行形式化描述，建立起精确的数学模型，再从这个模型出发，进行滤波器的设计与实现工作。

本文建立一个简单的线性测量系统模型，测量与移动目标之间的距离，即单个变量。假设当前时间的距离和前一时间的距离是相同的，所以选择A=1，不存在控制量，u（k）=0。根据公式（1）可以得出预测方程：

x（k）=y（k-1）

根据公式（2）可以得出预测方差方程：

p1（k）=p（k-1）+Q

根据公式（3）可以得出滤波后的最优估算方程：

y（k）=x（k-1）+Kg（k）（z（k）-x（k-1））

根据公式（4）可以得出卡尔曼滤波增益方程：

Kg（k）=p1（k）/（p1（k）+R）

根据公式（5）可以得出k状态下的方差方程：

p（k）=（1-Kg（k））*p1（k）

根据上述建立的数学模型，给定初始的预测值x（0）、方差p（0）以及一组观测数据z，即可实现对该组测量数据的卡尔曼滤波。

3     Matlab仿真

采用Matlab对上述建立的数学模型进行仿真，检测卡尔曼滤波的效果和影响，采用一组工程应用中的观测数据，由于卡尔曼的递推特性，预测值可以随意赋值，方差的初始值可以取非0 的任何值。

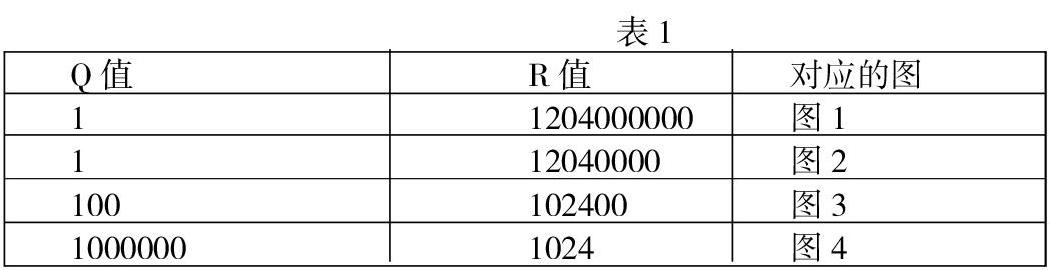
通过调整过程噪声和测量噪声的协方差Q和R的值可以调节卡尔曼滤波的效果及滤波数据的实时性。仿真结果见图2、图3、图4、图5，选择的Q和R的值见表1。由滤波效果可以看出：Q值主要影响滤波效果，值越大，滤波效果越差，值越小滤波效果越显著;R值主要影响滤波后数据的实时性，值越大，滤波后数据的实时性越差，值越小滤波后数据的实时性越好。

根据上述仿真结论得知，在实际应用过程中，可以根据系统的需求在滤波效果和实时性方面做出选择，即选择不同的Q和R值。

4结束语

本文介绍了卡尔曼滤波的原理，依据其系统方程和观测方程推导出了卡尔曼滤波的五个递推方程，在此基础上实现建立了最简单的线性离散系统数学模型，通过Matlab对其进行仿真，通过仿真实验结果得出系统噪声和观测噪声的协方差是影响滤波效果和实时性的因素，在实际应用中可以依据系统的需求在两者之间选择。

参考文献：

[1] 彭丁聪.卡尔曼滤波的基本原理及应用.软件导刊.2009.

[2] 张满生.张学庄.卡尔曼滤波器及其工程应用.计算机技术与自动化.2008.