IMM算法在空中复杂机动目标跟踪中的应用

王耀林 盖梦欧 周敏

摘  要：随着雷达技术的不断成熟，雷达跟踪领域涌现出了大量的跟踪算法，目前，交互式多模型算法凭借其精准的跟踪能力和优越的性能已逐步代替其他的目标跟踪方法被广泛应用到雷达航迹跟踪的各个领域。通过对IMM算法的研究发现建立IMM的CV、CA、CT运动模型并结合使用扩展卡尔曼滤波可以有效提高跟踪精度。基于MATLAB实验仿真表明改进后的IMM算法能以较高精度输出被跟踪目标的状态信息，取得了良好的跟踪效果。

关键词：目标航迹跟踪;交互式多模型;滤波器;跟踪精度

中图分类号：TN953;TP212      文献标识码：A 文章编号：2096-4706（2020）13-0009-03

Abstract：With the continuous maturity of radar technology，a large number of tracking algorithms have emerged in the field of radar tracking. At present，the interacting multiple model algorithm has been widely applied in various fields of radar track tracking by virtue of its accurate tracking ability and superior performance，which has gradually replaced other target tracking methods. Through the study of IMM algorithm，it is found that the establishment of CV，CA and CT motion models of IMM and the combination of extended Kalman filter can effectively improve the tracking accuracy. Experimental simulation based on MATLAB shows that the improved IMM algorithm can output the state information of the tracked target with high precision and achieve good tracking effect.

Keywords：target flight path tracking;interacting multiple model;filter;tracking accuracy

0  引  言

目标跟踪系统中的运动状态普遍有两种：机动状态和非机动状态。现代作战体系中，大多数目标的运动状态都是变化不定、实时更新的，各目标运动的非线性程度不尽相同，而卡尔曼滤波仅能够在线性高斯模型的条件下对目标状态做出最优的估计，虽然有些非線性系统可以近似看成线性系统从而直接用卡尔曼滤波来估计目标的运动状态[1]，但为了不对系统状态的估计精度造成影响，大多数系统如雷达预警系统不能仅用线性微分方程描述。因此，本文针对校内雷达目标跟踪项目中存在的非线性系统跟踪误差率大、跟踪精度损失严重等问题进行深入分析，在交互式多模型（IMM）算法中的滤波方法选用扩展卡尔曼滤波（EKF），扩展卡尔曼滤波的实现是以传统卡尔曼滤波为基础，利用特定的线性化换算将非线性系统滤波问题转化为近似的线性滤波问题，从而达到对非线性系统状态的准确跟踪和精准预测。

1  IMM算法的原理

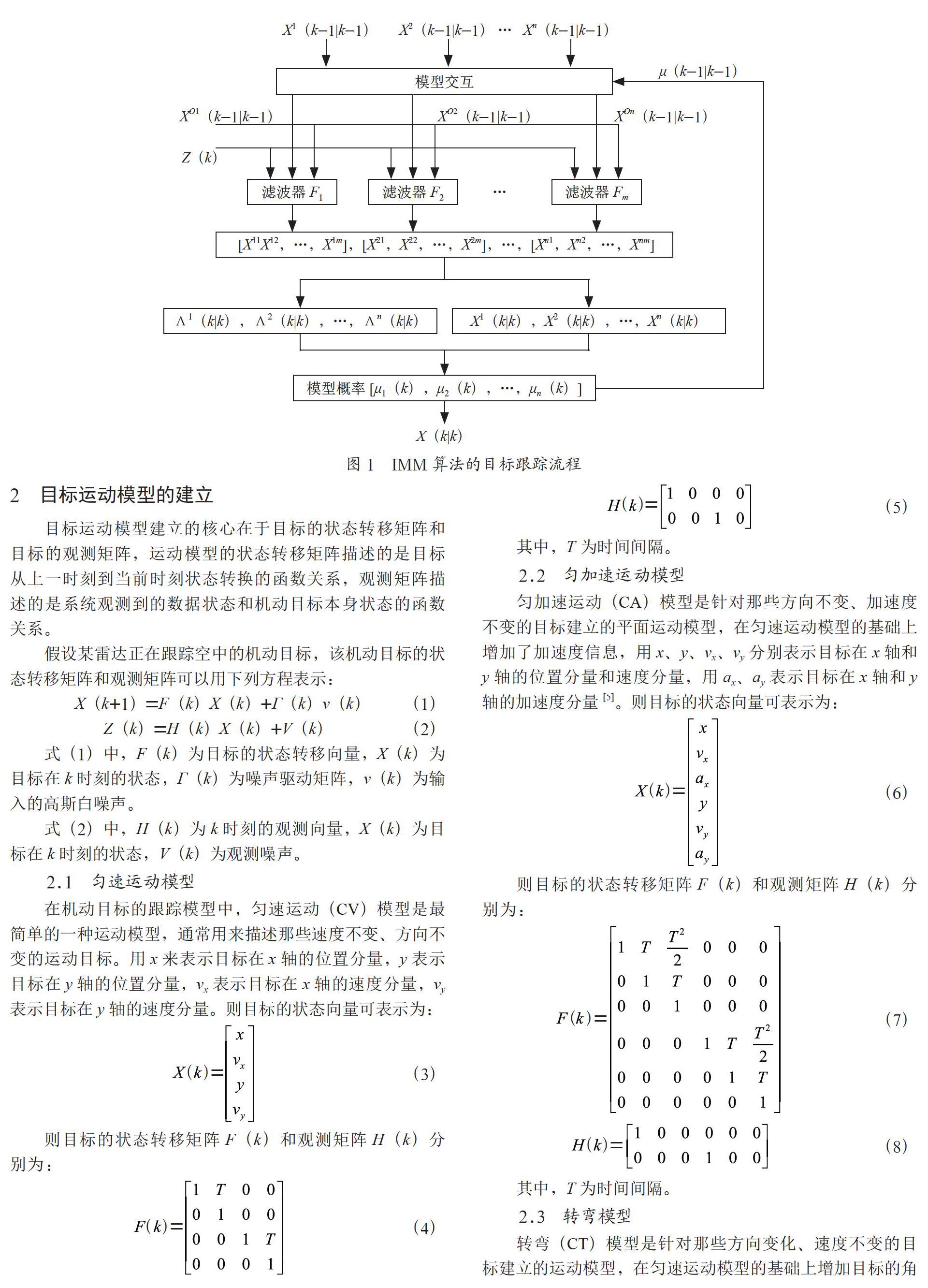
滤波的目的是估计与预测系统当前时刻和未来时刻的运动状态，包括被观测目标的位置、速度和加速度等状态信息。IMM算法根据被跟踪对象的运动状态的系统模型，采用模型滤波算法，将各个模型的状态估计加权组合得出最终滤波状态的估计值[2]。而这些模型应该包含被跟踪对象所有可能的运动状态，各个模型之间的切换服从马尔可夫过程。IMM算法的目标跟踪流程如图1所示。

IMM算法的处理流程可以分为四个部分，分别为：输入交互、滤波器滤波、模型概率更新和输出交互[3]。

1.1  输入交互

把k-1时刻第j个滤波器的状态估计输出X j（k-1|k-1）（j=1，2，3，…，n）作为输入，与上一时刻每个模型的概率μ（k-1|k-1）结合计算得出本次滤波的混合交互状态和混合交互协方差[4]。X j（k-1|k-1）根据模型概率μ（k-1|k-1）在各模型之间进行交互后得到的结果为XOj（k-1|k-1）（j=1，2，3，…，n）。

1.2  滤波器滤波

XOj（k-1|k-1）（j=1，2，3，…，n）经过各自的滤波器滤波之后，得到了k时刻各个模型的状态估计X j（k-1|k-1）（j=1，2，3，…，n）和似然函数Λj（k|k）（j=1，2，3，…，n）。

1.3  模型概率更新

各个模型概率的更新是根据各个模型的似然函数计算的，计算完成后得到k时刻各个模型的概率μ（k-1|k-1）。

1.4  输出交互

输出交互是指利用k时刻各个模型的状态估计和模型概率进行输出融合，最终得到的结果X（k|k）即为k时刻的状态估计值。

2  目标运动模型的建立

目标运动模型建立的核心在于目标的状态转移矩阵和目标的观测矩阵，运动模型的状态转移矩阵描述的是目标从上一时刻到当前时刻状态转换的函数关系，观测矩阵描述的是系统观测到的数据状态和机动目标本身状态的函数关系。

3  扩展卡尔曼滤波

为了更进一步提高目标跟踪的准确性，考虑到绝大多数目标运动的非线性情况，本文选择更合适的扩展卡尔曼滤波来完成非线性条件下对机动目标的跟踪，这样可以使得IMM算法在对高机动非线性目标进行跟踪的误差率远远低于基于卡尔曼滤波的IMM算法，跟踪效果的发散率得到明显下降。

扩展卡尔曼滤波的实现核心是通过泰勒公式对方程进行变换，将非线性方程的当前估计值展开，去除二阶以上项，就变成了卡尔曼滤波能够处理的线性方程，再用卡尔曼滤波进行处理。展开后的状态方程和观测方程分别为：

得到了目标的状态方程和观测方程后，就可以由上一時刻的观测值得出当前时刻的观测值，然后结合观测矩阵推导出下一时刻的滤波增益，最后进行更新就可以得到当前时刻的状态和协方差，然后进入到下一时刻。整个滤波过程是一个不断迭代的过程，直到完成对目标的跟踪[7]。

4  实验仿真与分析

MATLAB仿真迭代100次的结果如图2所示，目标的起始位置坐标为（999.3，985.1），在10～30 s期间进行了持续的15°的左转，在40～60 s期间进行了持续的4°的右转，在80～90 s又进行了持续的15°左转，其余时间做匀速运动。由此可见，该目标的运动状态出现了多次变化，但是在各个时间段，基于IMM模型的输出轨迹几乎与目标的真实轨迹完全重合，跟踪效果较为优秀

5  结  论

在跟踪空中的机动目标时，使用了扩展卡尔曼滤波的IMM算法在原有算法的基础上对跟踪精度做了进一步的提升。同时由于使用了多个目标运动模型，使得在目标进行变换机动甚至频繁转弯的情况下依然能够保持对目标的跟踪，即使有时会出现跟踪误差较大的情况，IMM算法也能很快修复，保持良好的跟踪效果。

同时得出IMM算法的几点不足如下，为后续的改进提供了方向：（1）由于IMM算法中存在多个滤波器并行运行的情况，所以对雷达系统的性能有较高的要求;（2）改进后的IMM算法使用了扩展卡尔曼滤波替换原来的卡尔曼滤波，虽然解决了对非典型系统的跟踪问题，但是相比于卡尔曼滤波，扩展卡尔曼滤波的计算复杂，计算量较大，适用性不强;（3）虽然改进后的滤波器能达到较好的跟踪效果，但是避免不了滤波器的单一性，在高机动环境下跟踪精度下降较快。

参考文献：

[1] 张英坤.扩展卡尔曼滤波在非线性系统中的应用 [J].中国科技信息，2018（7）：71-72.

[2] 赵慧.多传感器信息融合目标跟踪算法研究 [D].广州：华南理工大学，2014.

[3] 李秋旭.复杂环境下多传感器目标跟踪技术研究 [D].西安：西安电子科技大学，2018.

[4] 唐劲松，何友，王国宏.一种自适应α、β、γ滤波算法 [J].火力与指挥控制，1995（2）：32-36.

[5] 高春艳，董鹏，高涵，等.EKF交互多模型算法在目标跟踪的应用 [J].机械设计与制造，2020（2）：284-287.

[6] 魏喜庆，王社阳，李瑞康.基于自适应IMM算法的高超声速飞行器轨迹预测 [J].上海航天，2016，33（2）：27-31.

[7] 黄小平，王岩.卡尔曼滤波原理及应用——MATLAB仿真 [M].北京：电子工业出版社，2015：77-79.

作者简介：王耀林（1996—），男，满族，辽宁凤城人，硕士，研究方向：系统监控与网络管理技术;盖梦欧（1990—），女，汉

族，辽宁沈阳人，硕士，研究方向：物理教学;周敏（1995—），女，汉族，辽宁锦州人，硕士，研究方向：物联网技术及应用。