基于LCD-LLTSA的电动汽车电机轴承故障特征频率提取
2020-11-06史素敏杨春长
史素敏, 杨春长, 王 斐
(1. 商丘学院 机械与电气信息学院, 河南 商丘 476000; 2. 32148部队, 河南 驻马店 463000; 3. 陆军工程大学 一系, 河北 石家庄 050003)
1 引 言
局部特征尺度分解(local characteristic-scale decomposition, LCD)能够将复杂的机械故障振动信号自适应地分解成一系列的内禀尺度分量(intrinsic scale component, ISC),有效地提取故障信号的特征信息[4,5]。相比于经验模态分解(EMD)[6],LCD基线信号是通过线性变换得到,因此在求取ISC分量的过程中不需要太大的迭代次数,运算速度更快,同时ISC分量包含的故障信息更多[4]。但是,LCD分解得到的所有ISC分量中,一部分为有用ISC分量,一部分为干扰ISC分量,同时干扰ISC分量中同样会包含有有用信息,因此如何对其进行选择就尤为关键,而目前比较常用的相关性分析也有可能排除有用的信息[7,8]。假如将故障信号经过LCD分解依次得到ISC分量从上往下排列成一个矩阵,那么就可以把这个矩阵看成是一组包含多种信息的高维信号,采用某种降维算法对这该信号进行降维处理,并对降维后信号进行重构,那么就可以在不损失有用信息的情况下,有效地削弱干扰信息,更加突出故障特征。而作为目前比较常用流行学习算法之一的线性局部切空间排列[9](linear local tangent space algorithm, LLTSA)对非线性信号具有很强的分析处理能力,特别是在机械故障诊断领域,它可以有效地挖掘潜在的故障信息,受到了很多学者的青睐[10~13]。
基于此,本文把LCD和LLTSA二者结合,用于对轴承故障信号的分解和故障信息获得,并通过包络分析提取故障特征频率,仿真信号和实例均验证了该方法的有效性。
2 LCD方法
LCD有一个假设,那就是原始信号x(t)是由多个ISC构成的,并且所有ISC分量两两独立,其分解步骤如下:
1) 确定x(t)的所有极值点及时刻(Xk,τk),k=1,2,3,…,M。这样,x(t)就被Xk和Xk+1这2个点分成了若干段,在每段上对x(t)进行线性变换,得到:

(1)

2) 将Hk连接得到H1(t),并令P1(t)=x(t)-H1(t)。
3) 如P1(t)满足ISC分量的判据条件,则ISC1(t)=P1(t)。反之,把P1(t)作为原始信号并重复1)和2)两个步骤,循环k次,直到Pk(t)满足判据条件,此时,ISC1(t)=Pk(t)。
4) 令r1=x(t)-ISC1(t),并将r1作为原始信号重复步骤1)~3),循环n次,得到n个满足判据的ISC分量,直到rn为一单调函数为止。
于是有:
(2)
3 LLTSA基本原理
LLTSA主要是寻找一个转换矩阵A,使得A可以将RD空间中的数据集XORG映射为Rd空间的数据集Y=[y1,…,yN],即:
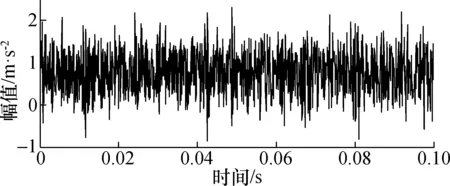
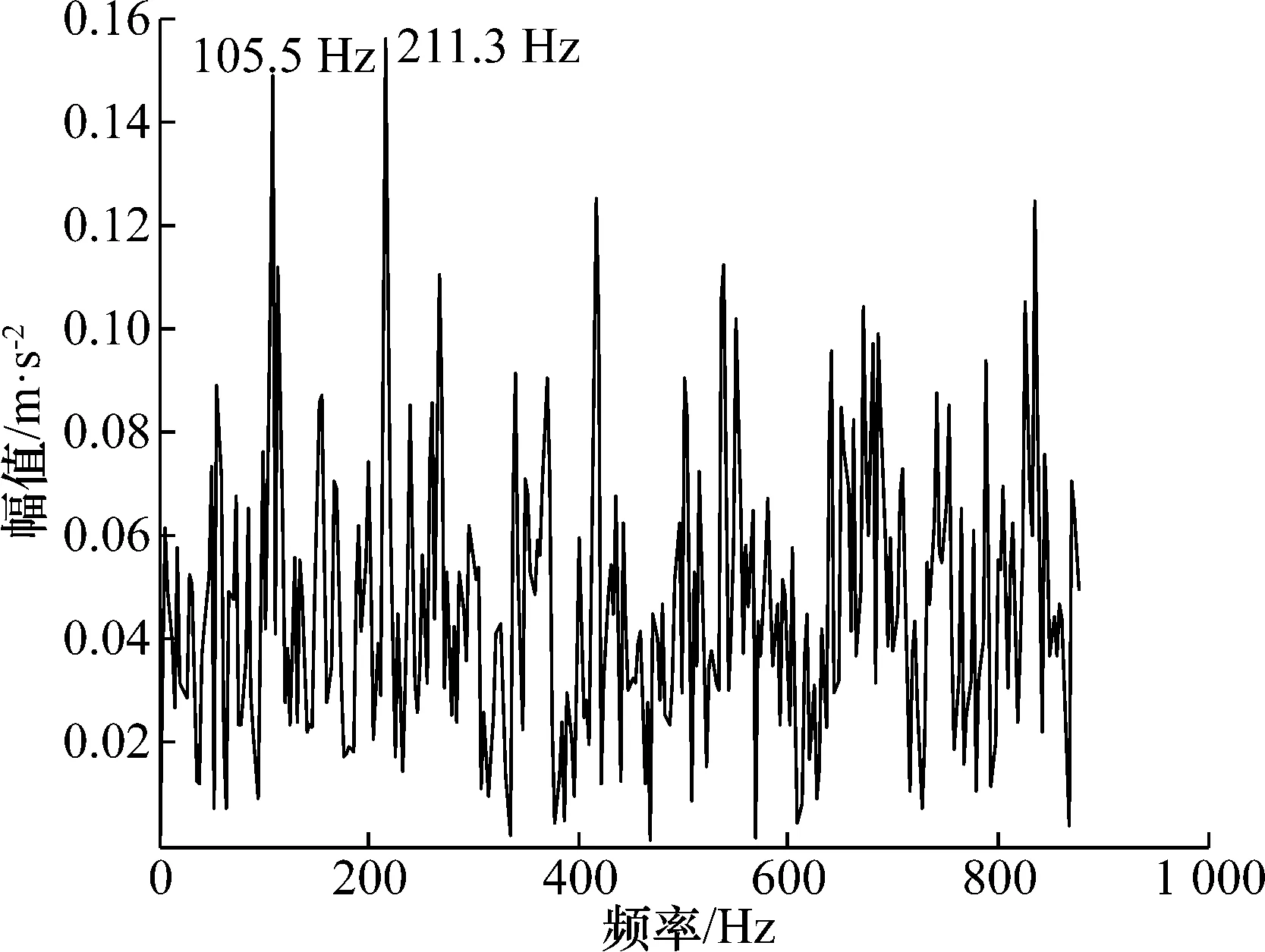
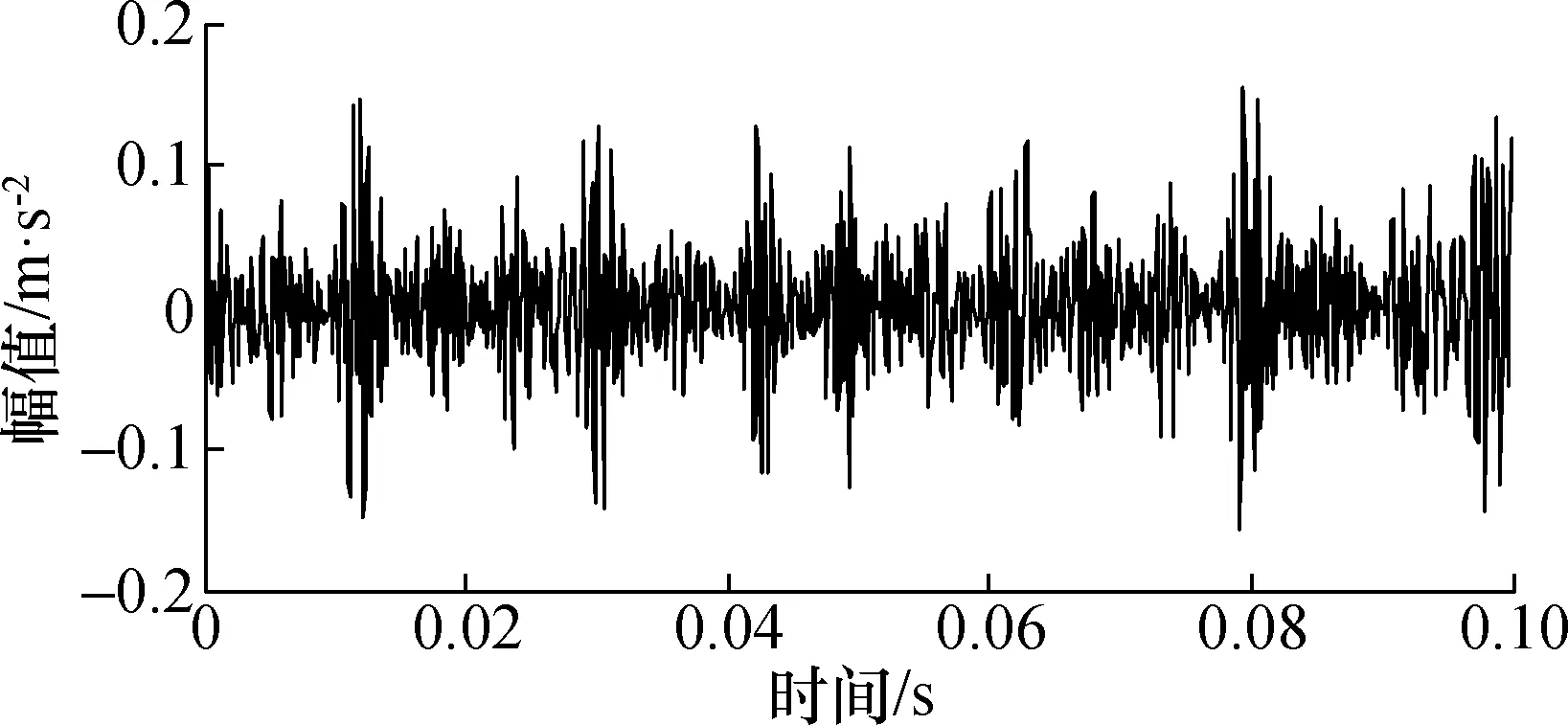
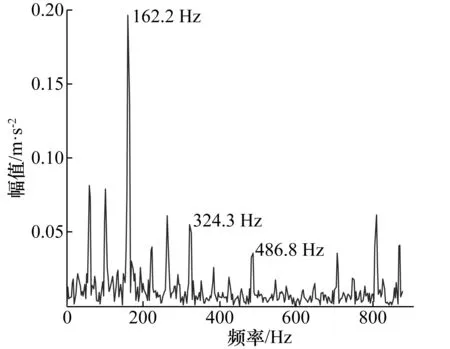
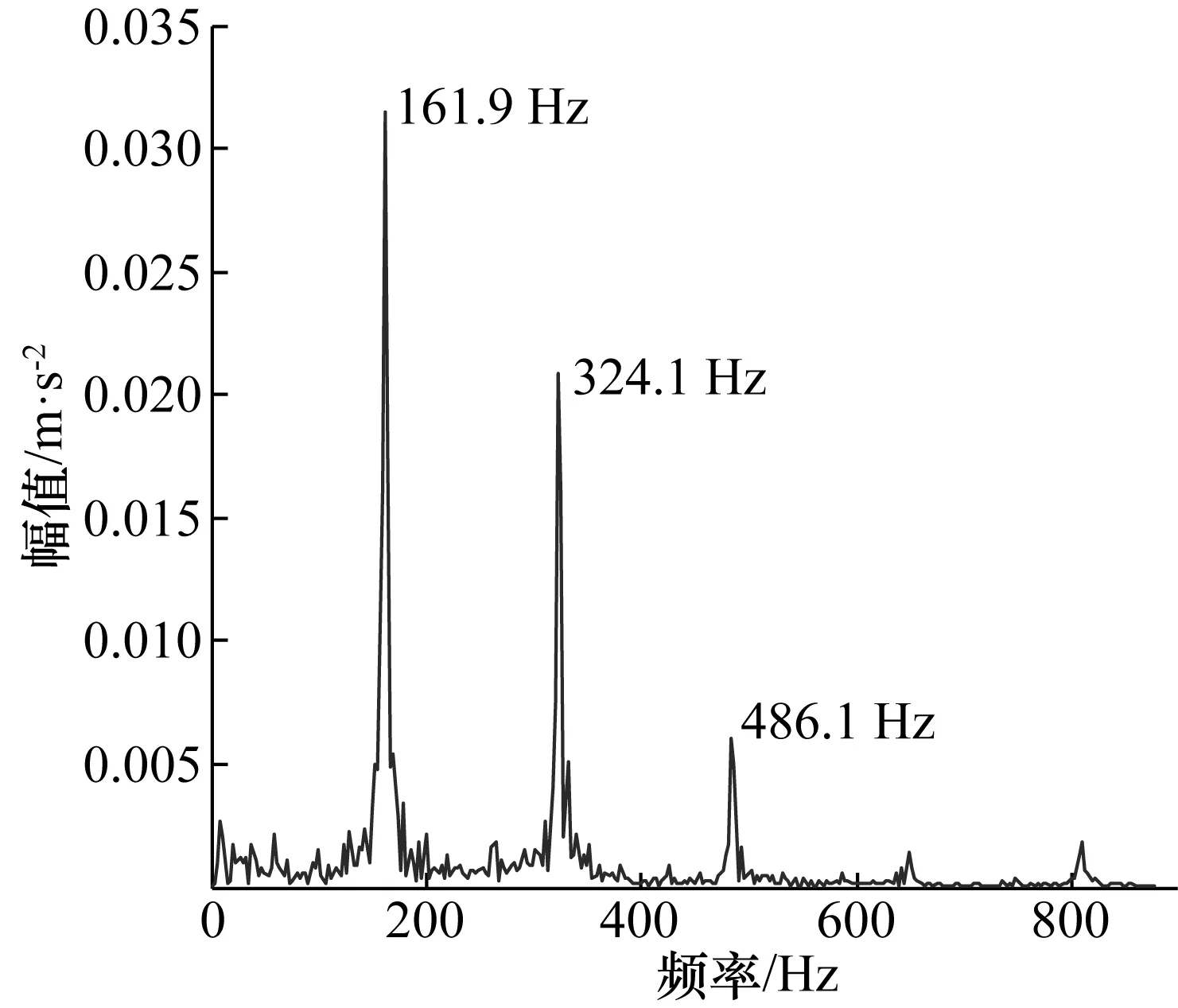
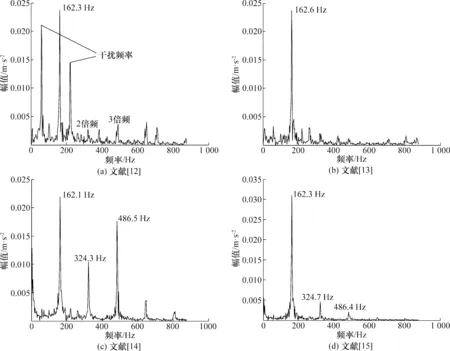
Y=ATXORGHN,d (3) 式中:HN=I-eeT/N为中心矩阵;I为单位矩阵;e为所有元素为1的N维列向量。Y为XORG潜在的d维非线性流行。 LLTSA主要有以下几个步骤: 1) 为达到降噪效果,先使用PCA(转换矩阵为APCA)对XORG进行映射得到X。 2) 采用K-近邻法(KNN)找到数据点xi的k个同类近似点xj。 3) 计算由XiHk(Xi=[xi1,…,xik])的d个最大特征值对应d个特征矢量构成的矩阵Vi。其中Hk=I-eeT/k,i=1,…,N。 4) 通过局部累加构造矩阵B为: B(Ii,Ii)←B(Ii,Ii)+WiWiT (4) 初始化B=0,式中Ii={ii,…,ik}表示xi的k个近邻点的索引集,Wi=Hk(i-ViViT)。 5)计算广义特征问题的特征值和特征矢量: XHNBHNXTα=λXHNXTα (5) 与特征值λ1,λ2,…,λn(λ1<λ2…<λn)对应的特征矢量解为α1,α2,…,αd,则ALLTSA=(α1,α2,…,αd),因此转换矩阵A=APCA×ALLTSA,X→Y=ATXORGHN。 4 基于LCD-LLTSA的轴承故障特征频率提取方法 方法流程如图1所示。 图1 方法流程图Fig.1 Flow chart 方法主要步骤如下: 1) 采用LCD对长度为N轴承原始故障信号x(t)进行分解,得到n个ISC分量。 2) 将n个ISC分量组成一个n×N维的ISC分量矩阵,记为: X=[ISC1,ISC2,…,ISCn] (6) 使用LLTSA对X进行降维,得到一个m×N的矩阵Y,记作: Y=[y1,y2,…,ym],m≤n (7) 3)将Y的各行y1,y2,…,ym相加便得重构信号y(t)。相比于x(t),y(t)减少了噪声以及次要特征的干扰,增强了故障信息。 4)对y(t)进行包络分析,提取故障特征频率,判定故障状态。 首先对仿真信号进行分析,仿真信号如下: s(t)=0.3cos(90 π t+0.5sin(30 π t))+ 0.2sin(240 π t)+N(t) 该信号由调频调幅信号和正弦信号叠加而成,其中基频为45 Hz、调频为15 Hz、正弦信号的频率为120 Hz,N(t)为白噪声,强度为1。该信号时域图和频谱图见图2所示。 图2 仿真信号及其频谱Fig.2 Simulation signal and its frequency spectrum 按照第3节所述步骤,首先利用LCD对s(t)分解,获得了5个ISC分量以及1个余量。然后将5个ISC分量组成分量矩阵,并采用LLTSA进行降维(设置目标维数m=2,邻域参数k=7),最后得到重构信号及其频谱如图3所示。 图3 重构信号及其频谱Fig.3 Reconstruction signal and its frequency spectrum 对比图2和图3可以发现,相比于原信号,重构信号中的噪声成分明显减少,基频、调频、正弦信号频率等信息更为明显,可以有效地获取仿真信号的频率信息。 实验数据来源于模型电动汽车电机轴承故障模拟实验平台,实验中,电动机转速控制在1 772 r/min左右(转频29.53 Hz),采样频率为12 kHz,采集了轴承外圈故障、内圈故障和滚动体故障3种状态的振动信号。根据相关计算公式和轴承型号参数,计算得轴承故障特征频率如表1所示。 表1 轴承故障频率Tab.1 Fault frequency of bearingHz 首先,截取数据长度为1 200个采样点的轴承外圈故障信号进行分析,得到其时域波形和包络谱分别如图4和图5所示。观察图4和图5可知,图4几乎看不到信号的周期性特征,图5中虽然也可以找到105.5 Hz和211.3 Hz等与外圈故障特征频率相近的频率成分,但其他干扰频率同样很明显,不易进行区分。 图4 轴承外圈故障波形Fig.4 Waveform and frequency spectrum of bearing with outer race fault 图5 外圈故障信号包络谱Fig.5 Hilbert envelope spectrum of outer fault 然后,对该信号进行LCD分解,得到6个ISC分量和1个余量,如图6所示。按照第4节所述步骤,将6个ISC分量组成ISC分量矩阵,然后通过LLTSA对ISC分量矩阵进行降维(其中,目标维数m=3,邻域参数k=7),最后得到重构信号,如图7所示,其中的周期性特征明显比图4要强。图8给出了重构信号Hilbert包络分析的结果,从中可以清晰的看到频率29.31 Hz和105.6 Hz以及它的倍频,29.31 Hz与转频29.53 Hz相对应,105.6 Hz及其倍频和外圈故障特征频率105.9 Hz相对应,相比于如图5所示原始信号包络谱,图9中干扰频率少,外圈故障特征频率信息更明显。 图6 LCD分解结果Fig.6 LCD decomposition result 图7 重构信号Fig.7 Reconstruction signal 图8 外圈故障重构信号的包络谱Fig.8 Hilbert envelope spectrum after reconstruction of outer fault 图9和图10分别为内圈故障原始信号和重构信号的包络谱。对比图9和图10,从图9中虽然可以看到159.2,318.3,477.8 Hz等频率成分,和轴承内圈故障的1倍、2倍和3倍频相对应,但同时还有干扰频率成分和边频带的存在,而图10除了能够看到内圈故障特征频率及其倍频外,几乎没有干扰成分的存在,对内圈故障的判断效果明显比图9要好。 图9 内圈故障信号包络谱Fig.9 Hilbert envelope spectrum of inner fault 图10 内圈故障重构信号的包络谱Fig.10 Hilbert envelope spectrum after reconstruction of inner fault 因此, LCD和LLTSA的结合可以有效提取轴承故障特征频率。这种方法有2个优点:一是直接将所有ISC分量组成矩阵进行降维,不需要对有用ISC进行选择,这就避免了有用ISC分量选择的盲目性;二是利用LLTSA可以降低原始信号中的干扰成分,增强有效的故障信息。轴承3种故障模式特征频率的有效提取验证了这2点优势。 此外,还对文献[12~15]中的方法进行了研究和应用。文献[12]中是采用互相关系数的方式来确定有用ISC分量个数并进行信号重构,文献[13]则是采用滑动峭度相关性准则来确定有用ISC分量个数并进行信号重构,而文献[14,15]中的特征频率提取方法则是完全不同于本文。因此,本文以轴承内圈故障特征频率提取为例,将上述4种参考文献中的方法和本文方法进行对比,以验证本文方法的有效性,图11给出了上述参考文献中方法的实验结果。 图11 参考文献中方法实验结果Fig.11 Experiment results of method in citation 图11(a)中虽然可以明显看到与内圈故障特征频率对应的162.3 Hz及其倍频,但是特征频率附近同样存在着其他频率成分且较为突出,对内圈故障的辨识具有一定的干扰。这可能是因为通过互相关系数方法把包含有干扰ISC分量选择成了有用ISC分量,进而造成重构信号中包含了干扰成分。图11(b)中同样可以明显看到与内圈故障特征频率相对应的162.6 Hz,且干扰频率的幅值得到了大幅度的降低,可以较为有效的辨识内圈故障,但倍频成分同样被降低,并不突出。这可能是因为基于滑动峭度相关性准则的有用ISC分量选择方法是在互相关系数方法上的改进,可以更好的消除干扰成分,但同样的,也把一部分有用的信息排除了。图11(c)和图11(d)中无论是内圈故障特征频率还是其倍频都可以清晰准确地被看到,而且干扰频率少,可以有效地对内圈故障进行辨识,和图10的不同之处就在于特征频率及其倍频的幅值有差异。 对比图10和图11可以得出如下结论:本文方法相比于文献[12,13]要好,比文献[15]略好,和文献[14]相当。上述分析表明本文方法可以有效应用于轴承的故障特征频率提取,具有一定的优势。 本文提出一种基于LCD和LLTSA结合的轴承故障特征频率提取新方法。利用LCD的自适应分解优势可以得到故障信号不同频段的ISC分量,而LLTSA可以有效地对ISC分量进行降维和完成信号重构,这即可有效保留ISC分量中的有用成分,同时也能最大限度的消除噪声。二者的结合可以较为准确地找到故障特征频率,具有一定的效果。
5 方法验证
5.1 仿真分析


5.2 实例分析



6 结 论
