改进遗传算法在CMP终点检测的应用
2020-11-06郑永军狄韦宇
郑永军, 狄韦宇, 罗 哉
(中国计量大学 计量测试工程学院,浙江 杭州 310018)
1 引 言
化学机械抛光(chemical mechanical polishing,CMP)集化学腐蚀与传统机械研磨于一体,是目前最佳也是唯一可以实现薄膜抛光与全局平坦化的技术,其改进将直接影响集成电路技术的发展[1,2]。目前CMP终点检测主要分为离线终点检测和在线终点检测。其中离线终点检测是根据不同产品,对样品进行试验抛光确定抛光时间与速度的关系,以此为基础进行CMP抛光。但是CMP抛光过程中,抛光垫温度、抛光液残留等均会造成二次影响,所以离线法实施简单但存在精度不高的现象。在线终点检测是目前发展趋势。然而CMP中硅片被抛光表面完全向下靠在抛光垫上,使得在线实时监测十分困难。目前这方面的研究大多基于摩擦力、温度、电机电流、声学膜厚追踪、光学等原理[3],但存在计算速度不够快的现状,或对薄膜材料有一定要求。光学法可以适用于大多数的绝缘薄膜或多晶硅抛光后的薄膜,且精度高,发展前景广阔。终点检测是CMP中重要的一环,终点判定过早则造成欠抛,判定过晚则造成过抛,都影响成品率,因此实时的终点判定对时间的要求性极高,如何快速进行终点检测是一大难题。
遗传算法(genetic algorithm,GA)是模拟自然界遗传机理的一种全局搜索方法[4]。GA不依赖初值,鲁棒性强,广泛应用于非线性实际问题,但变量过多时导致解空间过大,易早熟,局部搜索能力弱[5]。Güngör T和Saka B[6]将遗传算法应用于反射光谱法,将计算得到的折射率n、消光系数k与实际值相比较,误差小于0.1%。但GA在后期收敛性差,可以应用非线性单纯形法优化GA,提升局部搜索能力。反射光谱法具有测量操作方便简单、精度高等突出优点[7],但是必须选择合适的色散模型,且测量数据需精确,否则会对结果造成较大影响。El-Naggar A M等[8]通过反射光谱法并使用包络法反演了Si基底上的GaN薄膜的光学常数,结果与公布的数据之间有良好的一致性。
激光反射法是以激光作为光源照射薄膜,得到反射光谱,最后计算得到膜厚与薄膜折射率、入射角度的关系式,但是折射率计算公式需要对参数进行不断地调试。此方法优点是测量范围大,虽然具有较好的空间相干性,但是激光光源相干长度太长,在薄膜上下表面反射产生多余的条纹影响测量结果,且实现较为困难,需要长时间调试才能用于工业检测。白光光源操作简单、速度快,所需仪器造价低,适合工业检测[9]。SiO2薄膜是一种重要的薄膜材料,具有低折射率和吸收率、高硬度、低热膨胀系数、耐摩擦、抗腐蚀等优点,被广泛应用于光学薄膜元件、半导体集成电路、电子器件、传感器、化学催化、生物医学等领域[10,11]。
本文提出一种基于光学反射法的快速CMP终点检测方法。其基于SiO2薄膜在白光光源下的反射光谱,采用一种基于非线性单纯形法优化遗传算法的混合算法对薄膜反射率进行拟合,将拟合结果得到的膜厚与反射率对应关系得到参照表,以实时反射率与预设膜厚反射率的差方和、以及200~1 200 nm 波段内反射率平均值作为特征值,动态抛光时跟踪特征值及其变化趋势,对照拟合得到的参照表,当特征值误差小于某阈值时则认为达到抛光终点。
2 反射光谱法拟合原理
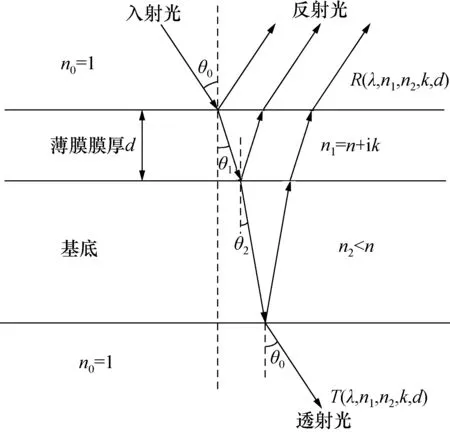
图1 薄膜的反射与透射图Fig.1 Reflection and transmission of the film
在复折射率为n+ik的膜层上镀上厚度为d的均匀薄膜,入射光线垂直薄膜入射。图1为入射光穿过镀膜基底并射入空气中的示意图。图2为正入射时单层薄膜反射率随波长的变化曲线。

图2 不同膜厚下反射率随波长的变化关系图Fig.2 Relationship between reflectance and wavelength under different film thicknesses
SiO2薄膜n≫k,k可忽略。反射率R与折射率n、膜厚d的关系式为[12]:
(1)
当薄膜的光学厚度刚好为λ/4的偶数倍时,在反射率图上可以得到极值点,这些极值点称为偶极值点;同理光学厚度刚好为λ/4的奇数倍时,这些极值点称为奇极值点。奇数和偶数阶有序参数分别对应于反射光谱的最大值和最小值。
图3为反射光谱的包络线图。
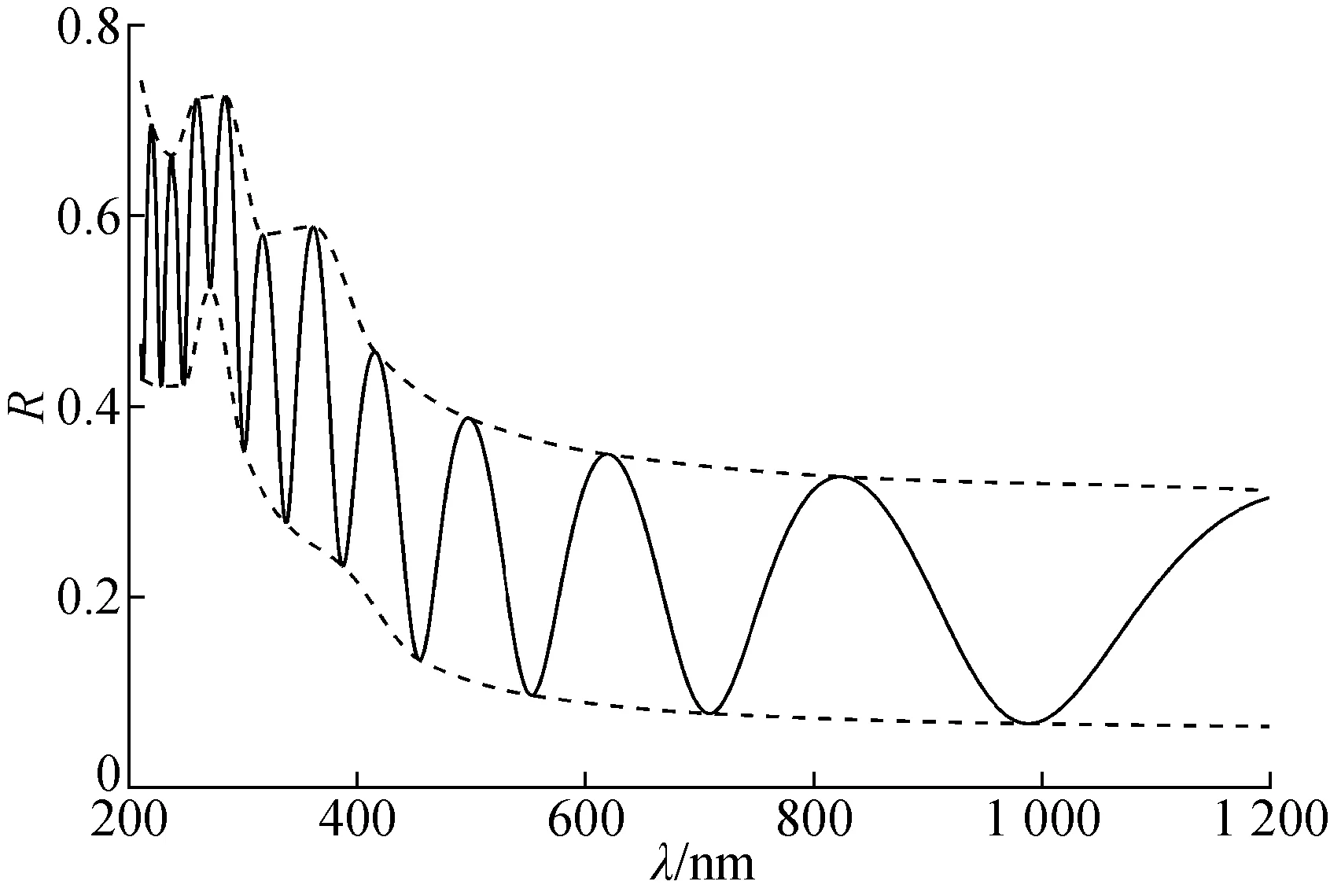
图3 反射光谱的包络线图Fig.3 Envelopes of reflectance spectrum
上下包络线极值点函数方程[12]分别为:
(2)
(3)
式中:a=n1-1;b=n1+1;c=n1-n2;d=n1+n2; e=n1-n22; f=n1+n22;g=64n2(n1-1)2n4;x=e-αd,α是吸收系数,α=4 π k/λ。
在某一波段范围内,2个连续奇极值点所对应的波长分别为λ1、λ3,可得到:
(4)
式中:m为波峰/波谷级数,为整数。
由式(4)可得到厚度d为:

由于光学参数折射率、消光系数各自和光波波长并不是简单的对应关系[13],其复杂对应关系归结起来主要是由介质材料的色散模型所决定[14],SiO2薄膜适用于Cauchy模型,其公式为:
n(λ)=A1+B1/λ2+C1/λ4
(6)
由于可见光光谱范围内,λ4非常大,因此在精度要求不高情况下可忽略第3项。其中A1、B1是进行全局优化所要解的常数。
本文采用光谱拟合法,基本思路是:在已知光学参数和膜厚条件下可以求出对应的反射率,然而光学参数和膜厚是所求的值,需要给这些参量设定某一组特定值进行反演,求得对应的反射率,当该值和实际的反射率之间的偏差逼近0时,则认为此时预设的参数值就是待测薄膜的参数。
采用的评价函数为:
(7)
式中:A1、B1、d为拟合参数;λS、λX分别为采样点的上下限波长;R(A1、B1、d)为计算值,R(λ)为试验测量值。
f值越小,表示计算值与实测值越接近,算法计算越准确, f最小时所得到的参数值就是最佳参数解。
3 自适应单纯形遗传算法
GA是一种启发式的并行全局优化方法,特点是算法独立于求解域,对初始条件依赖性低,可以求解复杂的优化问题[15]。非线性单纯形法,是一种用于解决非线性无约束优化问题的方法。将可行解形化,选择性的挑选解作为顶点,通过收缩、扩展等变形操作,沿着可行域边界变换顶点,目的是使得变形后所得新顶点的函数值更优,通过反复的变形直到得到理想的最优解或者判定问题无界[16,17]。
传统遗传算法在算法后期收敛时,收敛速度慢,当参数数量多、搜索空间范围大时计算时间久;非线性单纯形法对初始值要求高,计算快。考虑到GA对初始值要求低,且非线性单纯形法的高计算效率,将两者适当的结合,使用单纯形法优化GA的局部搜索能力。
本文采用的混合算法基本流程图如图4所示。

图4 混合算法的流程图Fig.4 Flow chart of the hybrid algorithm
具体步骤如下:
(1) 初始化。设定GA种群数量大小为60,初始进化代数t为0,最高进化代数为100,采用二进制编码,设定自适应交叉概率Pc和自适应变异概率Pm,以及算法停止规则:f<0.005、运行不低于150次且连续10代最大适应度值没有变化。
(2) 适应度计算。对种群中的每一个个体计算适应度值,并将适应度值由大到小进行排序。适应度值越高表示该个体越适应环境,越容易保留下来;反之则容易被淘汰。
(3) 选择操作。采用精英保留策略,按照适应度从高到低,选择适应度最高的6个个体,保留到下一代。余下的54个个体,随机分成18组,每组3个,另外在保留的6个个体中随机选取两个加入到每一组,即每组都有5个个体组成,把每一个个体视为单纯形的顶点,每个顶点的适应度值就是函数值,用单纯形法计算新的点。由18组数据组成了18个单纯形,产生18个新点存入下一代。剩下的再由原来的60个个体经过交叉变异,产生36个后代存入下一代,保证每一代的总个体数目不变。
(4) 交叉与变异。将步骤(3)产生的60个个体,按照设定的交叉概率和变异概率进行种群的交叉与变异,生成t+1代种群。
(5) 终止检验。如果满足设定的算法终止规则,则停止;否则t=t+1,转步骤(2)。
交叉与异变概率通常选用固定值,然而相同的概率是不公平的,不能满足种群进化过程的要求。优秀个体需减少变化趋势,使之能够尽量的保存下来,而适应度低的个体则应增大交叉和变异概率,使不良的基因发生变化,从而加快收敛速率,提高算法的效率。算法初期时,种群需要较高的交叉和变异概率,扩大解空间,以达到较快寻找最优解的目的;而在收敛后期,应该减小交叉变异概率,缩小进化步长,以帮助种群在找到最优解后快速收敛。
动态正确变化的概率相较于定值概率理论上更能接近于过程中不同状态下的最佳概率。本文采用自适应交叉与变异概率,将概率设置成线性,公式分别为:
(8)
(9)
式中:fmean表示种群适应度平均值;fmax表示种群适应度最大值;f′表示要交叉的两个个体中较大的适应度值;f表示要变异个体的适应度值。这样通过设定Pc1和Pc2的值,可以将Pc、Pm的值进行自适应调整,一般选取(0,1)区间的值。这里取Pc1=Pc2=0.75,Pm1=Pm2=0.05。
4 实验与分析
实验采用的硬件装置如图5所示,主要包括白光光源、光谱仪、光纤探头等,其中光谱仪采用美国海洋光学的QE PRO,其具有高信噪比与高稳定性。具体步骤为:SiO2薄膜置于一定厚度的Si基底上,由白光光源发出的光,经由光纤,通过光纤探头垂直入射至样品表面,样品薄膜上表面和下表面反射光相干涉形成的干涉谱,由反射光纤探头接收,再由光纤传送到光谱仪,光谱仪连续记录反射信号,将测量数据传输到电脑,分析实验数据,最终通过拟合运算得到测量结果。

图5 硬件装置Fig.5 Hardware device
通过混合算法反演SiO2单层薄膜的光学常数n和膜厚d。图6为膜厚400 nm时R与λ的关系图,图7为膜厚400 nm时n与λ的关系图。由图7可见,膜厚为400 nm时,反演结果与测量结果基本一致,重合度较高,差方和小于0.001 5。

图6 膜厚为400 nm时R与λ的关系图Fig.6 Relationship between reflectance and wavelength when the film thickness is 400 nm

图7 膜厚为400 nm时n与λ的关系图Fig.7 Relationship between refractive index n and wavelength when the film thickness is 400 nm
由于膜厚超过一定厚度后SiO2薄膜消光系数k基本为0,故无需对k进行反演,并且SiO2薄膜在膜厚较小时的反射率曲线变化幅度缓慢,极值太小,导致误差较大。
表1是膜厚为400 nm时混合算法拟合结果,f为评价函数,f越小表示拟合度越高。拟合得到的膜厚d的平均相对误差为0.438%,n的平均相对误差为0.609%。
表2是膜厚从200 nm到1 000 nm分别采用GA和混合算法计算10次取平均值后的结果。从表中可以看出,由GA得到的d平均相对误差为1.070%,n平均相对误差为1.324%,且有膜厚误差超过10 nm;混合算法得到的d平均相对误差为0.210%,n平均相对误差为1.067%。混合算法在膜厚与折射率的拟合结果上优于GA。

表1 膜厚为400 nm时混合算法多次拟合结果Tab.1 Hybrid algorithm multiple fitting results when the film thickness is 400 nm

表2 混合算法和标准遗传算法拟合结果比较Tab.2 Comparison between hybrid algorithm and genetic algorithm
5 CMP终点判定特征值
记录试研磨时的反射率谱数据,使用混合算法计算拟合膜厚,得到不同膜厚条件下的反射率,作为研磨中的参考值。以200~1 200 nm波段内反射率的平均值为特征值,得到不同膜厚与特征值对应的关系,计算参考膜厚与实时膜厚的反射率光谱,求得差方和σ。
(10)
式中:N为取样点个数,可以取20、30或50等;Ra(λi)为实际检测反射率值;Rt(λi)为理论反射率值。
当特征值差值与差方和达到预先给定的范围即达到抛光终点,停止抛光。由于极值点附近反射率值对膜厚变化不敏感,需进行一定倍数的放大,再进行反演,同时实时计算膜厚与折射率从而加快计算速度,使得单次计算时间小于0.000 1 s。
图8所示为膜厚从1 000 nm逐步减少至200 nm时,200~1 200 nm波长范围内反射率的平均值。平均值变化趋势明显,随着膜厚的减少,呈现“减增减增减”的趋势。

图8 不同膜厚反射率平均值Fig.8 Average reflectance of different film thicknesses
以初始膜厚为800 nm,研磨目标膜厚为400 nm为例:图9为反射率平均值差与膜厚差的对应关系曲线,图10为取50个间隔采样点时,不同膜厚与研磨目标膜厚的σ变化曲线。反射率平均值变化趋势为先增后减再增,斜率为第二次递增,且反射率平均值差和σ均为0时,判定达到CMP终点,停止研磨。

图9 膜厚800 nm研磨至400 nm的特征值变化曲线Fig.9 Eigenvalue curve of film thickness from 800 nm to 400 nm

图10 膜厚800 nm研磨至400 nm的σ变化曲线Fig.10 Sum of squared errors of film thickness from 800 nm to 400 nm
6 结 论
针对CMP在线终点判定问题,首先提出了单纯形法与遗传算法相结合的改进混合算法,并通过光学反射法对SiO2薄膜光学常数进行拟合,膜厚平均相对误差小于0.21%,折射率平均相对误差小于1.07%。相较于标准遗传算法,拟合结果精度更高,计算时间也得到了改善。再以算法拟合后得到的膜厚与折射率之间的对应关系作为参照表,以200~1 200 nm 波段内反射率平均值作为特征值,通过跟踪该特征值及其变化趋势以及计算与预设膜厚反射率的差方和,可在极短时间内进行终点判断。
包络法求得初始膜厚要求薄膜具有一定厚度,否则峰谷值太少预估的膜厚会产生偏大的误差。下阶段工作中,可针对此种情况,在预估初始膜厚时采用多采样点拟合,设置稍大的差方和值对膜厚进行预估,并提高初始膜厚的精度,使得算法可以应用于更薄的薄膜。
本文提出的方法作为在线终点判定条件可节约设备成本,减少计算复杂性,更好地预测终点从而防止过度抛光,提高产量和质量。
