近红外光谱分析中的化学计量学算法研究新进展

张 进,胡 芸,周罗雄,李博岩*

(1.贵州医科大学 公共卫生学院 环境污染与疾病监控教育部重点实验室,贵州 贵阳 550025；2.贵州医科 大学 食品科学学院,贵州 贵阳 550025；3.贵州中烟工业有限责任公司 技术中心,贵州 贵阳 550009)

近红外(Near-infrared,NIR)光是一种介于红外和可见光吸收区域的电磁波，其波长范围与分子中含氢基团的振动倍频和合频能量一致，因此常被用于常量有机成分的检测。但随着实验技术和数学理论的发展，近红外光谱的应用范围也向微量组分[1]或无机成分[2]检测的领域拓展，主要方式包括：①利用富集技术对样品进行预处理以提高其相对含量[3]；②利用增强的方式放大检测信号[4]；③利用扰动近红外光谱技术增加有效信息含量，提高多元校正模型的检测限。例如新兴的水光谱组学综合利用了溶质周围水分子对目标组分吸收的放大作用以及多元校正算法数据挖掘的特点，实现对水体系中多种物质的检测和分析[5-7]。近红外光谱技术具有绿色、快捷的特点，其检测方式主要包括漫反射和透射两种。近红外光谱的漫反射检测技术可用于非接触式检测，从而在一定程度上避免了繁琐的样品预处理，为快速检测和过程控制提供了有效的手段。近红外光谱技术在科学研究和工业生产中具有广泛应用[8]，例如，石油冶炼[9]、农业加工[10-11]、医疗卫生[12-14]以及食品安全[15-16]等。

化学计量学(Chemometrics)是在机器学习的基础上发展起来的用以解决化学领域中实际问题的一门学科。近红外光谱的吸收强度相对较弱且重叠严重，很难通过常规的单变量分析得到准确结果。因此，化学计量学算法在近红外光谱分析应用中占有重要地位[17]，尤其在数据挖掘方面。利用化学计量学中的多元校正方法能够将近红外光谱的众多变量结合起来共同反映目标组分的性质。一般来说，近红外光谱的变量数众多、共线性严重，因而多采用二维算法建立近红外光谱模型，这些方法很难像高维算法一样产生唯一解[18]。因此，在实际应用中，大部分近红外光谱的建模算法均伴随着降维和严格的约束条件。譬如，主成分分析(Principal component analysis,PCA)是一种最常见的化学计量学算法，通过严格的正交和归一化约束，所有的近红外光谱变量均可被几个甚至十几个正交变量简化代替，再利用传统的最小二乘算法建立模型。

近红外光谱的数据预处理、信息变量选择、多元校正模型的建立以及有效模型转移算法是保证近红外光谱技术应用和模型预测效果的重要手段和方法。这些方法的功能主要为消除背景干扰、筛选信息变量以及消除外界扰动对预测准确性的影响。2003年，田高友等[19]评述了小波变换在近红外光谱预处理中的应用，指出小波变换能够有效提取信息以及消除背景干扰。褚小立等[20-21]总结了多种近红外光谱的变量选择和建模算法，并展示了部分算法的原理、具体计算过程和应用实例。2017年，张进等[22]全面综述了多种最新的模型转移算法，从算法的角度将其划分为基于多元校正、因子分析、人工神经网络、多任务学习和其他5类模型转移方法。张学博[23]、柳艳云[24]、宋相中[25]、Yun[26]等分别从不同角度总结了近红外光谱的变量选择、模型转移和多元校正算法。本文在此基础上综述了近年来针对近红外光谱技术的发展与应用提出的一系列化学计量学新算法，主要包括近5年的光谱预处理、光谱变量选择、多元校正和模型转移等算法。

1 光谱预处理算法

光谱预处理算法主要指利用平滑、求导、滤波等技术消除光谱中的噪声和背景干扰，提高模型预测效果的一类方法[27-29]。

由于近红外光谱的检测器信噪比不同，测量信号中会不同程度地包含噪声成分，使得建立的模型预测效果变差。在不严重损失有效信息的情况下，消除部分噪声可以提高信号的信噪比，能够在一定程度上提高模型的预测效果。从噪声分布的角度看，通常认为近红外光谱的噪声具有独立同分布的特点。因此，基于窗口移动技巧的平滑算法(Smoothing algorithm)能够有效降低光谱中的噪声成分。其中，最具代表性的方法为Savitzky-Golay算法[30]。该方法针对窗口范围中心的光谱数据点施加大权重，而边缘的光谱数据点施加较小的权重，进而通过去卷积的方式对数据进行平滑，具有计算速度快和平滑效果好的特点。尽管有观点指出近红外光谱中存在非等性噪声和相关噪声[31-32]，但平滑算法在一定程度上仍能够有效提高模型的预测效果[33-34]。

近红外光谱中大部分为样品吸收信号，还存在部分与样品发生弹性碰撞的散射信号[35]。此外，还可能包括与样品无关的信号，如仪器本身的基线，这部分信号通常称为背景。背景信号本身不包含样品信息，因此在建模过程中会影响模型的预测效果。常见的扣除背景信号的算法包括有限脉冲响应(Finite impulse response,FIR)[36]、多元散射校正(Multiplicative scatter correction,MSC)[35]、标准正态变换(Standard normal variate,SNV)[37]、正交投影(Orthogonal projections,OP)[38]、扩展多元信号校正(Extended multiplicative signal correction,EMSC)[39]。这些方法大都假设近红外光的散射符合一种特定的分布，因此在校正过程多使用平均光谱的信息作为参照。

从信号频率的分布角度看，近红外光谱的噪声具有相对较高的频率，而背景的频率相对较低，因此，对于特定频率成分有过滤效果的带通滤波器往往也具有降噪和背景扣除的功效。傅里叶变换(Fourier transform,FT)是一种利用不同频率的正、余弦叠加的形式表示原始信号的方法，对信号的频率分析效果显著。在实际应用中，通常用快速傅里叶变换(Fast Fourier transform,FFT)的方式进行傅里叶变换操作。但傅里叶变换缺乏在时域的分辨能力，故在近红外光谱实际分析中应用并不广泛。小波变换(Wavelet transform,WT)是一种多尺度的分析方式，用迅速衰减的小波基进行卷积操作，产生的小波系数同时具有时域和频域的分辨能力。长期的研究和应用证实小波变换是一种扣除背景和噪声的有效方法[40]。图1为小波变换光谱预处理示意图。由图1A可以看出sym12小波在时域迅速衰减的性质。图1B展示了sym12小波经快速傅里叶变换后的系数，sym12实际为通过一定频率信号的带通滤波器。图1C为1.0 s的模拟信号，其中0～0.5 s为低频，而0.5～1.0 s为高频。经过小波变换的系数(图1D)表明，其无论是在频率尺度上还是时间尺度上均有较好的分辨能力。

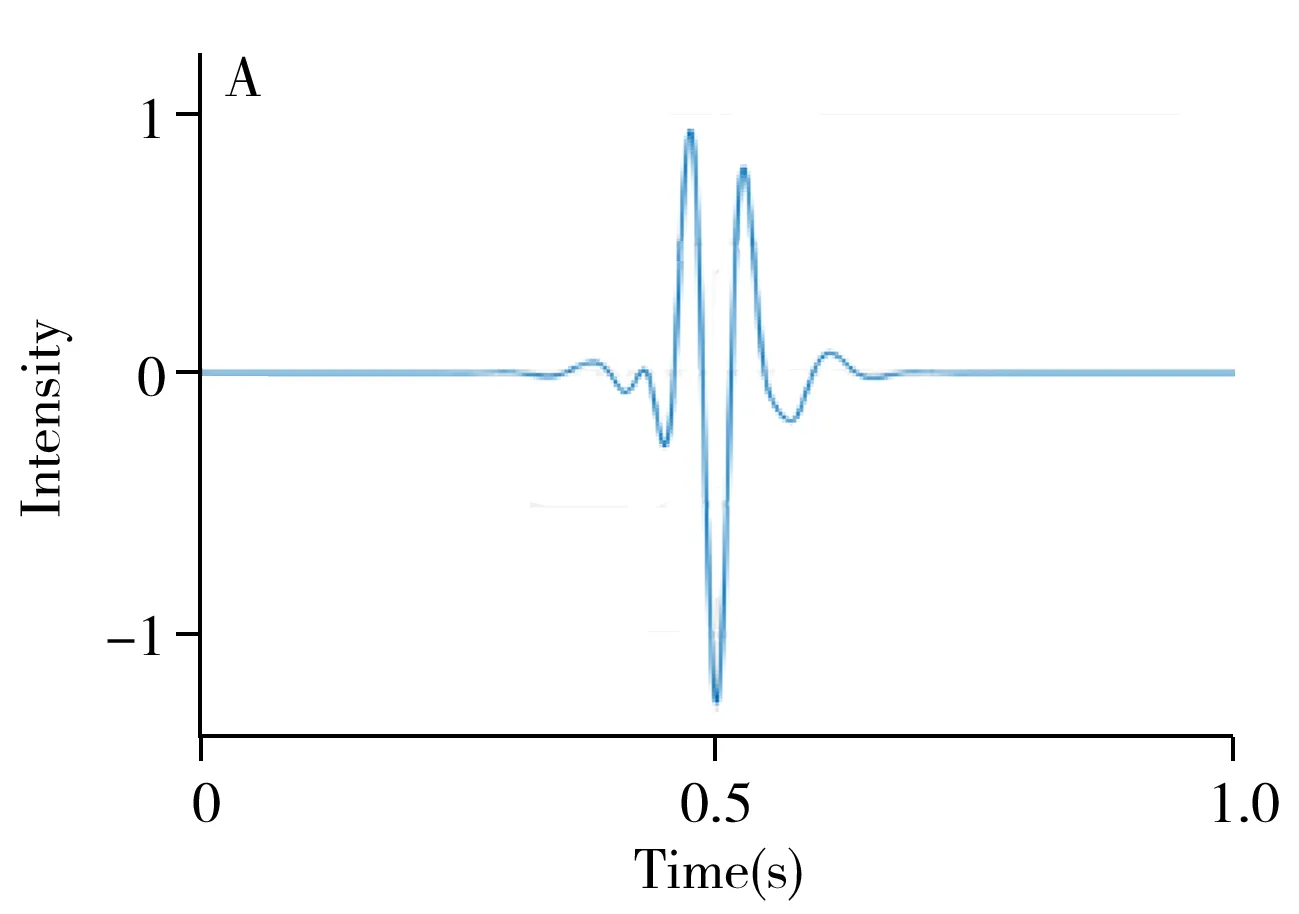
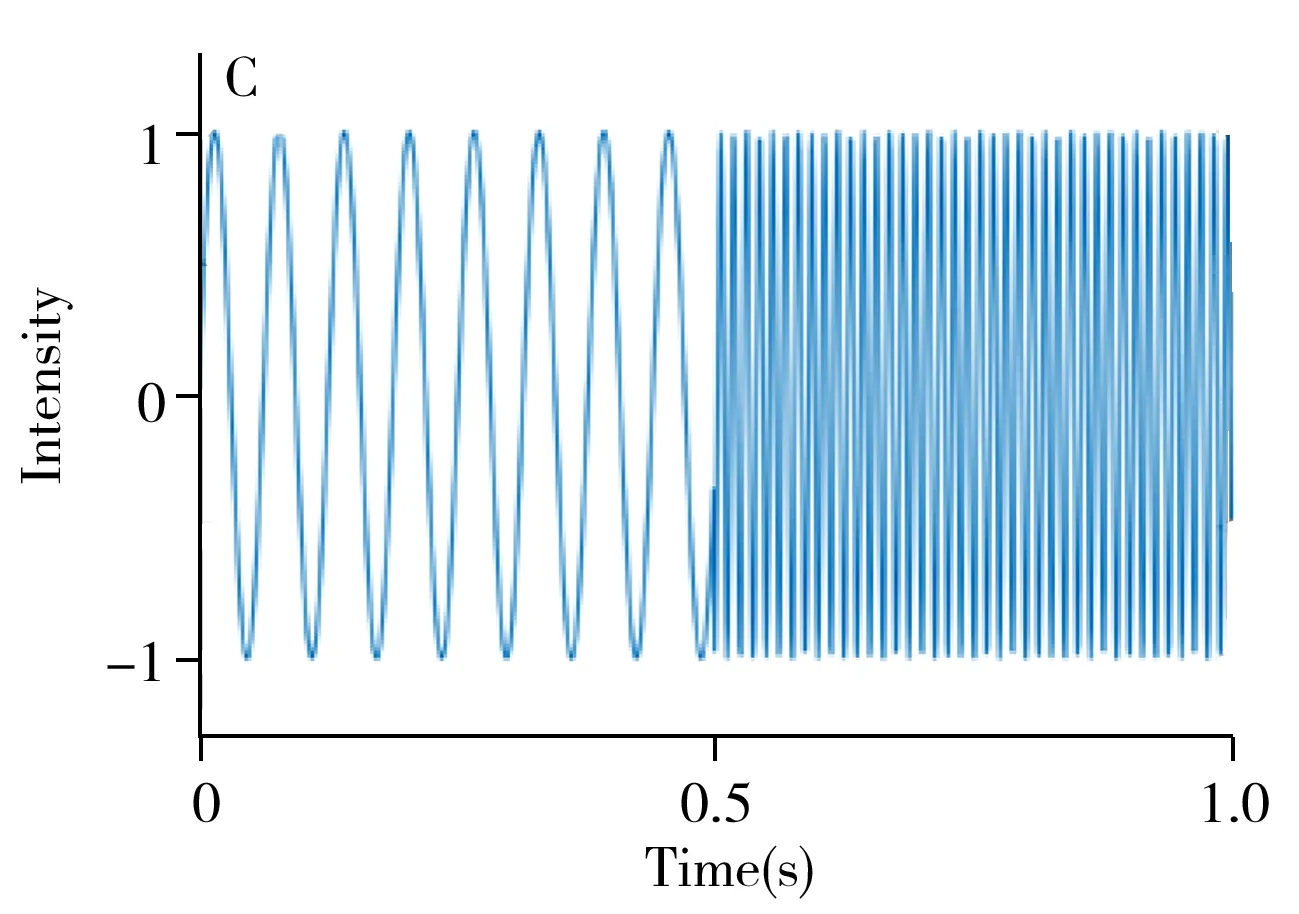
小波变换不仅能够消除低频背景和高频噪声，也是一种非常有效的数值求导方法。传统数值求导可以提高光谱分辨率，同时也会降低光谱的信噪比。小波变换求导法在提高光谱分辨率的同时可保证光谱的信噪比。Shao等[41]使用小波变换求导法处理水和乙醇的混合融合光谱，展现出更多的特征信息，建立了更加有效的定性定量模型。

加权多元散射校正(Weighted multiplicative scatter correction)[42]是一种结合了变量选择和多元散射校正的联合方法。该方法通过交替执行变量选择和多元校正过程，同时实现代表性变量选择与散射校正，得到的结果优于传统的光谱预处理算法。对数比值法(log-ratios)[43]则利用对数变化和数据标准化的联合方法进行散射校正，克服由尺寸效应(Size effect)引起的分析误差。这些联合方法同时考虑了多因素的共同作用，有望进一步消除近红外光谱中的散射效应，从而提高模型分析的准确度。

2 光谱变量选择算法

近红外光谱的吸收区间大致可归属为含氢基团C—H、N—H、O—H和S—H基频分子振动的一、二、三级或更高级倍频及其合频[44]，如水分子的合频大致在5 155 cm-1,伸缩振动一级倍频在6 944 cm-1；N—H的伸缩振动一级倍频在6 666 cm-1；酚类和醇类的一级倍频在7 092 cm-1,二级倍频在10 000 cm-1。对于特定的体系目标组分，并非所有吸收变量能与之直接相关联。另外，仪器的非等性噪声等因素也会产生信噪比较低的光谱吸收变量，这些变量可对建模造成干扰，引起模型预测效果变差。光谱变量选择算法能够在众多近红外光谱吸收变量中选择特征性的信息变量，从而在一定程度上提高模型的准确性。

简单直观的变量选择方法是将所有的光谱变量做全排列，对每种可能的变量组合进行验证，找到一组最优的变量组合[45]。然而，对数以千计的近红外光谱变量，可能的组合数过于庞大，以目前的计算速度几乎无法完成。所以，利用优化算法进行变量选择是有效可行的策略。以模型的预测误差为优化目标，通过最小化目标函数寻找有效减低模型预测误差的变量组合，例如，启发式并行模拟退火算法(Heuristic and parallel simulated annealing algorithm)[46]等。此类算法在一定程度上能够选择部分特征性或代表性的变量，但其优化算法的设计尤为关键，直接影响计算效率和效果。

基于变量重要性判据的方法能够有效提高计算效率，例如，回归系数绝对值、回归系数的统计学参数stability、P值以及变量之间的冗余程度等。常见的方法有无信息变量删除(Uninformative variable elimination,UVE)[47]、蒙特卡罗-无信息变量删除(Monte Carlo-uninformative variable elimination,MC-UVE)[48-49]、随机测试(Randomization test,RT)[50]、竞争自适应重加权采样(Competitive adaptive reweighted sampling,CARS)[51]、双竞争自适应重加权采样(Double competitive adaptive reweighted sampling)[52]、置换正交波长选择(Replacement orthogonal wavelengths selection)[53]等。这些方法的计算效率和效果得到了进一步的提高，可以选出特征性或代表性的变量，有效提高了模型的预测准确性。

变量之间的协同效应包括正协同和负协同作用，可能增加变量选择的难度[54]。近红外光谱的变量选择过程往往会受到负协同变量的干扰，从而导致计算的变量重要性判据失去代表性。为充分考虑变量协同效应的影响，Zhang等[55]提出了一种基于变量排列组合的重要性判据——C值算法。该判据定义为每个变量在有限次排列组合中对预测误差的平均贡献，用线性模型拟合代表变量组合的采样矩阵和对应的交互验证误差向量，得到的回归系数即为C值。该方法基于变量直接排列组合的思路选择代表性变量，有望在存在正负变量协同效应时选出代表性变量。

收缩(Shrinkage)策略是一种改善变量选择效果的有效方法[56]。该方法通过多步变量选择代替单步选择，每一步均删除少量的干扰变量来收缩变量筛选的空间。该策略在CARS方法中被使用，显著提高了基于回归系数绝对值选择变量的效果。Zhang等[55]将收缩策略应用于更加高效的变量重要性判据C值中，提出了基于C值的多步变量选择(Multi-step variable selection based on C value,MSVC)方法。该方法充分利用C值对负协同效应变量的识别能力，通过多次反复剔除隐藏的负协同效应变量达到选择重要变量的目的，最终能够有效提高模型的预测准确性。

综合策略也是一种有效改善变量选择效果的方法。该方法的基本思路是同时或逐步采用多种方法进行变量选择，然后对结果进行综合评价。Zhang等[57]在此基础上提出了一种加权表决最小收缩和选择算子(Weighted voting strategy combined with least absolute shrinkage and selection operator)方法。此方法在有放回的重采样基础上综合考虑了稀疏正则化和回归系数的信息，可选出最具有代表性的变量。此外，排序预测选择(Ordered predictors selection)[58]、稳定自举软收缩方法(Stabilized bootstrapping soft shrinkage approach)[59]等也采用了类似综合策略进行变量选择。这些方法能够在原有的基础上改善变量选择，然而选择效果在很大程度上取决于对不同方法的平衡和综合利用度。

为了降低变量选择的难度，对近红外光谱进行分段处理也是一种有效的策略，因此衍生出了很多波段选择的方法。Zhang等[60]提出了基于排列组合的波段选择方法——启发式最优波段组合(Combination of heuristic optimal partner bands)，通过在光谱中选择冗余性最低的代表性变量，并以此为中心向周围扩展一定的宽度形成波段，再采用变量排列组合的思路选出具有协同效应的波段组合，从而提高C值的变量选择效率。区间组合优化(Interval combination optimization)[61]是一种等长度波段组合优化的方法。该方法将整个波段划分为若干等长的波段，然后采用变量选择的思路进行组合优化，在选择变量的同时大大降低了选择效率，而波段划分的合理性可能会显著影响最终变量选择的效果。

随着近红外水光谱组学[5-7]的发展，温度扰动相关的变量选择问题也逐渐凸显出来。此外变量选择往往涉及对多组不同扰动条件下的数据进行同时选择，需要兼顾扰动和目标组分的共同作用，选出对扰动和目标组分变化敏感的变量。Cui等[62]将变量选择的思路应用于温度依赖的水光谱组学数据中，选出与温度变化相关的代表性变量，从而显著降低了水光谱组学分析的复杂程度。

3 多元校正算法

多元校正是化学计量学算法中的重要组成部分，根据其研究目标是否离散，总体上可分为判别分析(即定性分析)与回归分析(即定量分析)。常见的多元校正方法包括多元线性回归(Multivariate linear regression,MLR)、主成分回归(Principal component regression,PCR)、偏最小二乘(Partial least squares,PLS)、支持向量机(Support vector machine,SVM)和人工神经网络(Artificial neural network,ANN)等。这些方法常与光谱预处理、变量选择、模型转移等算法联用，将近红外光谱中多个(或全部)变量结合起来共同反映研究目标的性质。

基于采样理论的模型组合方式，主要包括样本采样和变量采样两种，能够在一定范围内提高校正模型的预测能力。Bian等[63]提出一种基于变量空间采样偏最小二乘(Variable space boosting partial least squares,VS-BPLS)的模型组合方法，将一系列变量重采样的子模型通过加权的形式组合成一个总模型，并通过每个子模型能够解释光谱信号的总方差决定的其权重大小。作者使用两个近红外光谱数据集验证了该方法在一定程度上能够提高模型预测的准确性和稳定性。

近红外光谱的非线性可能会导致线性模型的预测结果变差。目标组分的浓度范围过大、光谱数据预处理方法的选择不当以及仪器漂移均可能引起近红外光谱与组分浓度的非线性关系问题。Liu等[64]提出一种在线LASSO(Just in time-least absolute shrinkage and the selection operator,JIT-Lasso)方法，用来解决在线近红外光谱由时序漂移引起的非线性响应问题。该方法首先定义了一种基于光谱距离与时序差加权的样本距离盘踞，然后根据校正集与验证集样品的距离对样本进行动态加权，建立随验证样品动态变化的模型，从而能够在一定程度上提高模型的预测准确度，降低预测误差。

陈增萍课题组提出光谱形变理论(Spectral shape deformation,SSD)[65]的多元校正框架。该方法认为传统线性校正模型对于非均相体系和异质性样本可能存在偏差，主要是由于近红外的光程可能随样品发生变化。基于此假设，对光程可变的样本进行光程修正，再建立多元校正模型，可得到更为准确的分析结果。

深度学习(Deep learning)是机器学习领域的一个新方向。近年来，图形处理器(Graphics processing unit,GPU)加速了数学计算的发展，使得训练深度学习模型不再困难。目前，深度学习的基本结构是由不同功能的层(Layer)组成的神经网络，包括卷积层(Convolution layer)、池化层(Pooling layer)、激活函数层(Activation function layer)、压平层(Flatten layer)、全联层(Full connection layer)、丢弃层(Dropout layer)、输入层(Input layer)和输出层(Output layer)等。其中卷积神经网络(Convolution neural network,CNN)是深度学习中最具代表性的一类模型。Zhang等[66]提出针对近红外光谱分析的CNN模型，由1个输入层、3个卷积层、1个压平层、1个全联层和1个输出层构成。对4组近红外光谱数据的验证结果表明，该模型的预测效果相比传统多元校正模型有所提高。Chen等[67]提出的点对点的卷积神经网络模型则由1个输入层、1个卷积层、1个激活函数层、1个全联层和1个输出层组成。组合卷积神经网络(Ensemble convolutional neural networks)策略[68]通过训练多个模型后进行加权组合，可以提高CNN在近红外光谱分子中的预测能力。对于近红外光谱的建模，深度学习已显现出一定的优势。然而，深度学习的“黑匣子”特性导致模型解释性相对较差；而且深度学习的模型也往往较复杂，易陷入局部最优的困境，因此需要较多样品才能训练出相对较好的模型。

近年来提出的极限学习机(Extreme learning machines,ELM)是一种结构非常简单的人工神经网络模型[69]。由于其泛化性能良好，学习速度比传统神经网络快很多倍，因此在诸多领域受到广泛关注。堆叠组合极限学习机(Stacked ensemble ELM,SE-ELM)[70]将近红外光谱分为若干区段，建立多个ELM模型，再用不同权重将这些模型组合起来。该方法对6组近红外光谱数据的验证结果表明其预测效果和泛化能力(即对未知样品的预测效果)均优于传统多元校正模型。此类模型的优点是计算速度快、预测效果好，而且通过多模型组合或方法间的联用可以进一步提高模型的泛化性能。

4 模型转移算法

近红外光谱易受外界因素干扰而发生扰动或变化，例如温度、湿度、样品形态、粒度以及仪器升级、更换等。通过在不同条件下采集的样本光谱建立函数转换关系校正光谱、模型系数或预测结果的方法称为模型转移方法。笔者总结了一些常见的模型转移算法[22]，主要包括斜率截距法(Slope/bias,S/B)[71]、专利算法(Shenks algorithm)[72]、直接标准化(Direct standardization,DS)[73]、分段直接标准化(Piecewise direct standardization,PDS)[73]、光谱空间转换(Spectral space transformation,SST)[74]、典型相关性分析(Canonical correlation analysis,CCA)[75]和交替三线性分解(Alternating tri-linear decomposition,ATLD)[76]等。这些方法大多能够有效消除光谱间的差异，提高模型的准确性和适用性。

近红外光谱的使用范围广泛，产生光谱差异的因素可能互相叠加，导致了模型转移的困难。针对多因素导致的光谱差异，Zhang等[77]提出了一种稳健的模型转移方法——多级同时成分分析(Multi-level simultaneous component analysis,MSCA)。该方法将外界环境扰动引起的光谱差异分为两部分：组分间的通用差异和特异性差异，通过分步依次校正这两部分的差异实现稳健的模型转移目的。

因子分析是将数据在低维空间中近似表达的一类方法。利用因子分析将高维空间中的光谱转移转化为低维空间中的抽象因子转移，能够有效降低模型转移的复杂程度。例如，联合唯一分块分析(Joint and unique multiblock analysis)[78]、域不变偏最小二乘(Domain-invariant partial-least-squares)[79]、仿射不变式(Affine invariance)[80-81]以及MSCA模型转移方法。Zhang等[82]在此基础上提出了一种基于权重系数的模型转移方法(Calibration transfer based on the weight matrix)，该方法在偏最小二乘权重系数的基础上构造模型转移函数，转化偏最小二乘权重为得分，将光谱间的转化变换为光谱与得分间的转化，简化了模型转移的复杂程度，提高了模型转移的可靠性。

基于拉格朗日乘子法的正则化方法不但能够实现模型的平滑、稀疏等特性，还能够自由结合多种约束实现模型转移和模型更新。此类方法通过超参数(Hyper-parameter)来平衡效率(目标函数)和模型复杂程度(约束条件)的关系，但需通过交互验证或外部验证决定合适的参数。Zhang等[83]在此基础上提出了一种基于岭回归的模型更新方法，将预测优化目标和模型系数的2范数约束相结合，实现了模型系数的更新，解决了由于仪器漂移或样本变化引起的模型预测能力和可靠性变差的问题。

模型组合方法在模型转移中也有应用。Chen等[84]提出了一种组合主成分分析、极限学习机和自适应迁移学习算法(TrAdaBoost algorithm)的模型转移方法，首先通过迭代提升的策略建立多个学习机，再通过加权将所有学习机综合起来建立一个适用于不同条件下的通用模型。该方法实际为一种全局建模的策略，思路简单，模型预测效果有所提高，但相对传统基于标准样品的模型转移策略略显不足。

一般来说，使用标准样品的模型转移方法的结果相对更加准确，然而其应用性受到限制。南开大学邵学广课题组提出了一系列无需标准样品的模型转移方法，例如，双模型策略(Dual model strategy)[85]、偏最小二乘校正(PLS-corrected)[86]和线性模型校正(Linear model correction,LMC)[87]方法。这些算法无需使用在不同仪器或条件下采集的标准样品的近红外光谱，即可实现不同条件下采集的光谱或模型预测值的校正。Zhang等[88]在LMC基础上提出的修正线性模型校正(Modified linear model correction,mLMC)方法利用拉格朗日乘子法，将预测优化目标函数与不同条件下模型系数相关性约束相结合，实现了对不同仪器设备基础上建立的分析模型高效、快速的无标准样品转移。

5 结论与展望

随着现代仪器制造技术的不断发展，近红外光谱仪逐渐向“微型化”的方向发展，更多地扮演着一种通用传感器角色，出现在各种工业生产和人民的生活中，例如：工业过程控制，超市中农产品、肉制品、奶制品、蛋类等日常检测。使用者也逐渐从专业检测分析科研人员转变为工人、市民和普通消费者。传统的化学计量学方法的应用往往需要谨慎的算法选择、参数调整等一系列过程，导致大量非专业人员望而却步。因此，新时代背景下的化学计量学方法正朝着“自动化”、“智能化”、“云计算”的方向发展，同时助力近红外光谱技术走出实验室，进入普通生活的千家万户。

随着“互联网+”和“大数据”时代的到来，近红外光谱的应用前景越来越广泛，多种传感器的联用现象也越来越普遍，同时化学计量学方法更多地考虑数据间的相互融合和补充。近红外光谱对水分、湿度、仪器状态等外界扰动非常敏感，可能会引起传统的化学计量学方法所建立的模型效果变差。如果将扰动看作补充信息的一种新维度，借助多种传感器提供的额外信息建立针对扰动的自适应算法，能够化干扰为信息，有效提高近红外光谱分析的准确程度。南开大学邵学广课题组提出了多种基于温度扰动的水光谱学算法，将温度扰动作为一种数据信息增强的手段，从而提高了近红外光谱分析的效果和技术使用范围。因此，新时代下化学计量学算法的发展应以“数据融合”和“相互补充”为导向，以助力近红外光谱检测分析技术向更加广泛、准确的方向发展和应用。