基于局部加权偏最小二乘的近红外光谱分析方法研究

马力文，郭 拓*，马晋芳，，史庆龙，肖环贤

(1.陕西科技大学 电子信息与人工智能学院,陕西 西安 710021；2.中山大学 南沙研究院，广东 广州 511458；3.江西保利制药有限公司，江西 赣州 341900)

现代中药工业生产过程十分复杂，基于指标成分的含量检测方法是中药质量控制的有效手段。因此，如何建立科学、高效的中药质量评价方法是中药现代化长期以来需要解决的难题。近红外(Near infrared，NIR)光谱分析技术作为一种快速、高效的检测手段，在中药生产过程中得到了广泛应用[1]。通过结合数学算法，对其近红外光谱数据与指标成分含量建立相关定量模型，以实现药物的定量分析。偏最小二乘法(PLS)作为目前近红外光谱分析中应用最广泛的线性建模方法[2]，通常用于拟合药物光谱与指标成分含量之间的线性关系。而在实际应用过程中，由于受仪器的非线性响应和固体样品颗粒大小的不均匀性等非线性行为的影响，PLS法难以发挥其作用[3-4]。局部加权偏最小二乘法(LWPLS)是对PLS法的有效改进，对每个测试集样本计算其在训练集样本上的权重，并通过加权的样本，对每一测试集样本建立局部的偏最小二乘模型，用多个局部线性模型来逼近非线性过程，该方法能在一定程度上放大光谱与性质之间的相关信息，从而使得预测结果更为准确[5]，故可以很好地解决药物光谱与指标成分含量之间为非线性关系的问题。

因此，本研究提出了基于局部加权偏最小二乘法，并结合相关系数法[6]进行波长优选，建立了对安胎丸进行指标成分定量的模型，同时与PLS算法建立的校正模型精度进行比较，旨在为定量模型的建立提供新算法。

1 原理与方法

1.1 局部加权偏最小二乘(LWPLS)算法

LWPLS的基本思想是当预测某个样本的理化性质指标时，首先计算该样本与训练集之间的相似性，并将此相似度值作为该样本的权重，此时判别样本是否相近的依据通常为马氏距离或欧氏距离[7]。本文选用欧氏距离作为度量工具，即以样本间的欧氏距离作为权重，记为δ。其建模预测流程如图1所示。

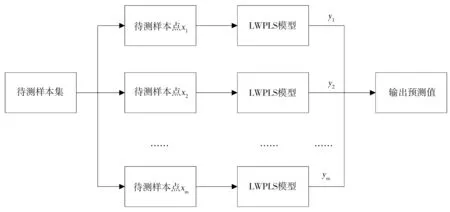
图1 LWPLS建模预测Fig.1 LWPLS modeling and prediction

假定光谱矩阵和性质矩阵分别为X(n×p)和Y(n×q)，其中n为样本数目，p为波长点数，q为性质数目。对于待测样本xm，首先根据下式计算它与其他校正集样本之间的距离：

(1)

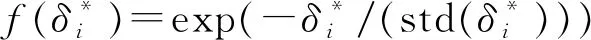
(2)

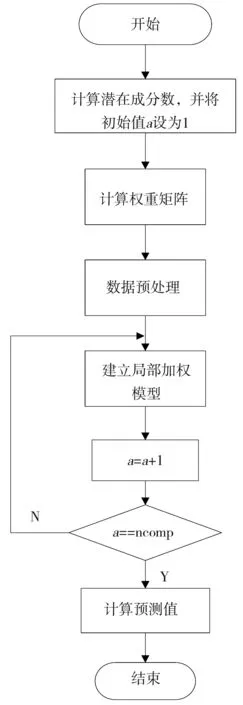
图2 LWPLS算法思想Fig.2 Algorithm idea of LWPLS

LWPLS算法思想如图2所示，主要包括以下几个步骤：

第一步：计算潜在成分数(ncomp)，设置其初值为a=1，采用留一交叉法，将样本分为n组训练集和验证集。在每一组中，用训练集样本建立的模型去预测验证集样本，当预测误差平方和最小时所对应的组号即为ncomp。

第二步：根据式(1)和(2)计算权重矩阵，并采用K-近邻(KNN)算法，在训练集中选取与待测样本xm之间欧氏距离最小的10个样本点，将这10个样本点所表示的集合记为X′，其对应的性质矩阵记为Y′。

第三步：对训练集矩阵以及待测样本进行预处理，计算Xa、Ya、Xma

国内设计咨询企业属于工程行业中技术性和专业性集中的企业，在企业的管理过程中，通常更加关注企业本身的技术层面。在财务管理中，仅注重成本核算，将财务人员视为“账房先生”，缺乏有效的成本控制意识。粗放式的管理模式，使得企业忽视成本管理，不深入探究项目成本管理模式，不进行项目成本效益横向对比分析，不开展工程产业链收益率分析，无法为企业提供准确数据支撑。

(3)

(4)

式中，1n为1的列向量，p=1,2,……,P;q=1,2,……,Q。

第四步：建立局部加权模型

(5)

(6)

待测样本点的得分：

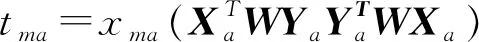
(7)

若a=ncomp，则跳至下一步；否则a=a+1，返回第四步。

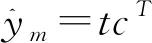
(8)

其中T为X的得分矩阵。

1.2 相关系数法

相关系数法是将校正集光谱矩阵中每个波长对应的吸光度向量xj与性质矩阵中的待测组分性质向量yi进行相关性计算，相关系数越大的波长，其信息量也越多。因此，可结合经验知识给定一个初始阈值，选取相关系数大于该阈值的波长参与建模。然后根据模型的精度调整阈值，从而确定最优的波段。相关系数r用下式计算[10-11]。

(9)

2 实验部分

2.1 数据集

本研究参考文献的光谱采集方法[12]，采用SupNIR1500近红外光谱仪，应用漫反射模式，设置波长扫描范围为1 000～1 800 nm，分辨率为2 nm，对3年生产的共21批安胎丸进行NIR光谱数据的采集；采用高效液相色谱法(HPLC)梯度洗脱，对21批安胎丸中的指标含量进行测定。将测得的安胎丸样本数据按3∶1∶1的比例分成训练集、验证集和测试集。首先随机挑选17个样本作为验证集，剩下的数据集采用X-Y共生矩阵法(Sample set partitioning based on Joint X-Y Distance，SPXY)算法分成训练集和验证集。具体结果见下表，原始数据见原文献。

表1 安胎丸样本集的分类结果Table 1 Classification results of Antai pill sample set

2.2 数据预处理

由于建模过程中，近红外光谱的校正集样本中可能混杂异常光谱，会直接影响到定量模型的精确度，进而影响指标成分的预测结果。因此，本研究首先采用马氏距离法[13]对异常样本进行剔除，此处两种指标成分的马氏距离的阈值分别设为1.112 6、1.266 0，然后建立模型。

近红外光谱的采集过程中，由于样品本身的状态、表面颗粒的不均匀程度以及仪器操作等因素的影响，导致出现光谱信息重叠及背景干扰的现象[14]。因此，建立模型之前需要对光谱数据进行预处理。在诸多的光谱预处理方法中，标准正态变量变换(SNV)可有效地消除因固体样品表面颗粒大小不均匀、样品表面光散射以及光程变化等引起的光谱噪声[15]。因此，本研究在LWPLS建模之前首先采用SNV对近红外光谱进行预处理，预处理前后的结果如图3所示。

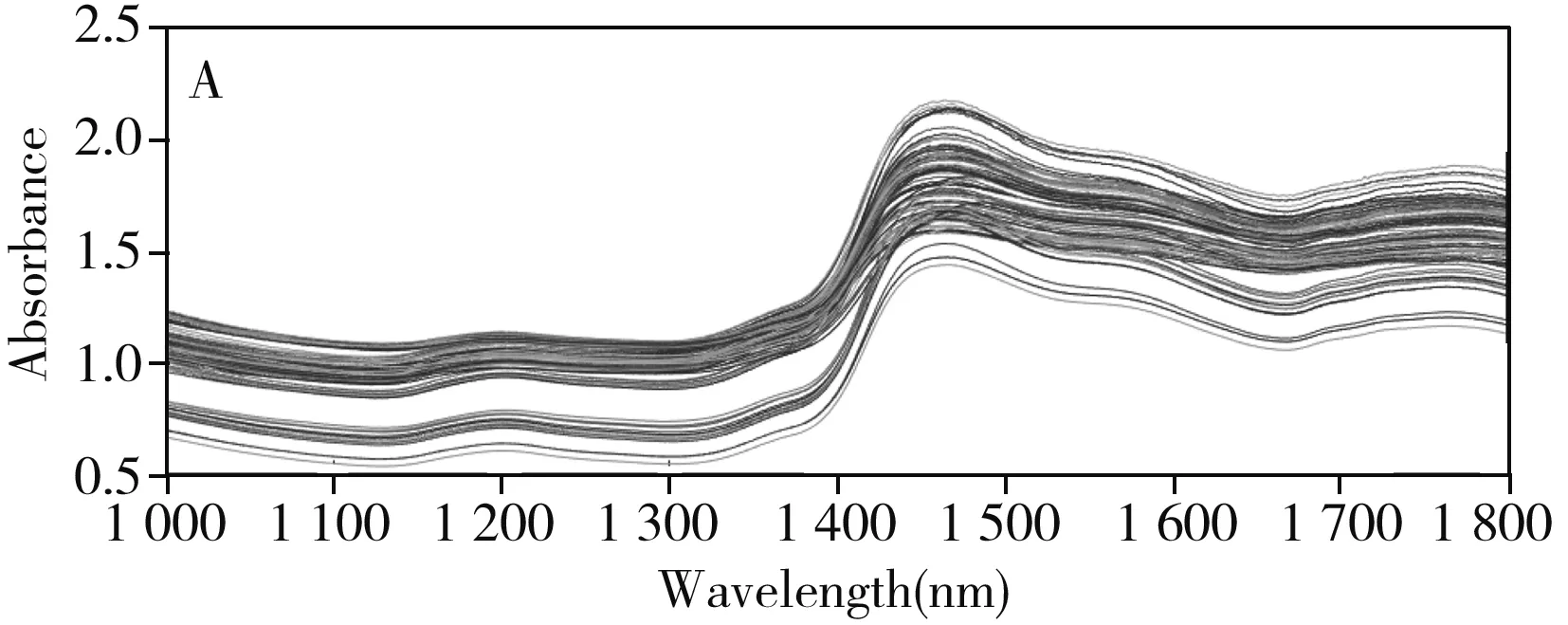
2.3 特征波长的选择

在近红外光谱技术的应用中，通常出现以下现象：由于波长之间有一定的相关信息，导致光谱信息中存在冗余信息，使得计算量较大[16]；由于人工误操作或者仪器自身的噪声，使得光谱某些波段会夹杂噪声，直接导致模型不稳定；或某些波段有可能受外界因素的影响导致吸光度异常，存在局部异常点。因此，NIR校正模型建立之前进行波长选择不仅可以使计算量减少，更能使参加建模的变量中有效信息增多，进而提高校正模型的预测精度[17]，增强稳健性。本文采用相关系数法进行波长选择，并对比了PLS与LWPLS算法的建模效果。

2.4 模型的建立与评价

采用KNN算法选取10个近邻样本，利用LWPLS结合相关系数法对安胎丸的训练集进行阿魏酸和洋川芎内酯A定量模型的建立。

模型的优劣主要以模型参数，如潜在成分数(ncomp)和权重函数的形状参数(h)、预测误差均方根(RMSEP)、相对预测误差(RE)及模型相关系数(R2)等作为评价指标，对定量模型的精度进行评估。

3 结果与分析

3.1 LWPLS建模参数优选

本研究利用SPXY算法对安胎丸样本进行训练集、验证集、测试集的划分，SNV对近红外光谱进行预处理，相关系数法进行波长选择，并分别结合LWPLS与PLS对安胎丸进行定量模型的建立。其中h是LWPLS中一个重要的参数，Lesnoff等[5]认为主成分数的h一般在0～1之间。因此，本研究将权重函数的h范围设定为0.1～0.9，在不同形状参数下比较模型的RMSEP。

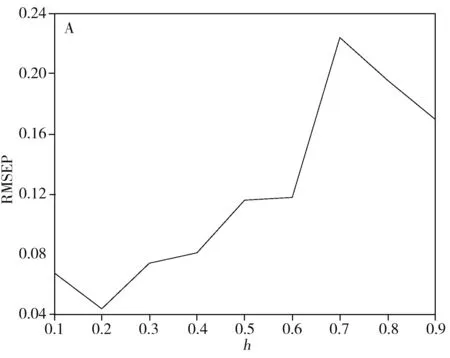
由图可知，对于指标成分阿魏酸，当h=0.2时，模型效果较好(RMSEP<0.05)；对于指标成分洋川芎内酯A，当h=0.1时，模型效果较好(RMSEP<0.08)。因此，本研究中阿魏酸的LWPLS模型的h设为0.2，洋川芎内酯A的LWPLS模型的h设为0.1。

3.2 两种定量建模方法对模型预测性能影响的对比分析

将阿魏酸和洋川芎内酯A两种指标成分的LWPLS模型验证结果与线性模型 PLS的验证结果进行对比。结果显示，两种指标的LWPLS模型的预测值与真值更接近1∶1，聚集性也优于PLS的结果，且LWPLS的结果未出现远离对角线的异常点。阿魏酸采用PLS和LWPLS建立定量模型的预测结果与真值的线性相关系数分别为0.886 2、0.985 8(见图5)；洋川芎内酯A采用PLS和采用LWPLS建立定量模型的线性相关系数分别为0.941 4、0.982 3。

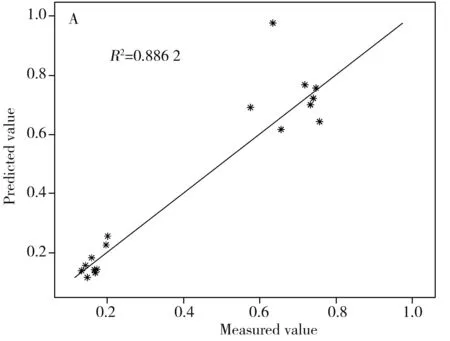
两种指标成分的预测结果与原结果的线性相关系数均大于0.88，其中LWPLS方法建立定量模型的预测结果的线性相关系数高于PLS方法，且LWPLS方法的线性相关系数更接近1，说明其预测结果更接近真值。

以下将模型参数中选择的波长数目、ncomp、h、RMSEP、RE与R2进行比较，结果见表2。由表2可以得出，采用LWPLS方法建立的模型，其R2分别由0.785 5、0.886 4上升至0.971 9、0.964 9，RMSEP分别由0.126 6、0.114 8降至0.043 8、0.077 1，RE也分别从12.66%、14.01%降低至9.18%、7.81%。数据表明：LWPLS方法使得模型的准确性和稳定性优于PLS方法，且模型的指标参数得到显著提高。

表2 安胎丸中指标成分定量模型参数的比较Table 2 Comparison of quantitative model parameter values of index components in Antai pills

4 结 论

本文研究的LWPLS算法，是针对每一测试集样本建立局部的PLS模型，将多个局部线性模型组合，其整体上为一个非线性模型。该算法成功应用于安胎丸指标成分的建模，并解决了线性建模方法PLS对非线性关系无法准确拟合的问题，提高了模型的性能与预测精度。该方法有望以较小的计算代价完成非线性模型的建立，并应用于实际生产过程的在线质量监测。