属性依赖度的纵横快速计算方法
2020-11-06吕丰
吕 丰
(广西大学 计算机与电子信息学院,南宁 530004)
0 引言
在处理高维数据时,特征选择是一种十分重要的降维方法,它从原始特征空间中通过使用某种评价准则去选择特征子集,属于常见的数据预处理方式.特征选择目前有很多种算法,包括最优化算法、随机搜索算法、启发式算法等[1-4].而在决策信息系统中,根据特征或特征子集的依赖度来定义特征的重要度,从而根据特征重要度来选择特征[5]158,是一种重要的启发式算法.粗糙集理论是近几十年来发展迅速的数据挖掘方法,已经大量地在各个领域中发挥巨大作用,研究者众[6-9].而属性约简是粗糙集理论核心内容之一,为了获得知识的属性约简,亦经常根据属性重要性来设计启发式约简算法.属性重要度与特征重要性,常常使用依赖度来定义,依赖度的计算速度,决定了特征选择或属性约简的速度,所以,在海量数据集中如何快速计算特征(属性)或特征集的依赖度,对于降低运算时间,提高运算效率具有十分重要的理论研究意义与应用价值.目前关于依赖度的计算,不少学者作了一些研究[10-12],提出了许多算法,大多算法的时间复杂度为O(|U|2×|C|2).而章夏杰等则提出了一种快速依赖度计算方法FDC[13]518,为依赖度的计算提供了一种新的思路,然而该算法仍存在不少重复无效的过程.本研究则提出一种改进算法,可以大大降低重复过程,减少运行时间,实例表明算法是可行有效的.
1 基础知识
定义1.1[14]1(决策信息系统,等价关系和等价类) 称四元组DIS=(U,C∪D,V,f)为决策信息系统,其中U={x1,x2,…,xn}为非空有限论域,C与D均为非空有限属性集合.C为条件属性集,D为决策属性集,常见情形是只有一个决策属性,C∩D=φ.V为属性值的集合,Vij=vij表示第i个对象在第j个属性下的取值.f:U×(C∪D)→V为信息函数,表示xi∈U,aj∈C∪D,f(xi,aj)=vij∈V.那么在条件属性子集B⊆C下的不可区分关系(等价关系)RB及所生成的等价类[x]RB分别为
RB={(x,y)∈U×U|∀b∈B,f(x,b)=f(y,b)},
(1)
[x]RB={y∈U|(x,y)∈RB}.
(2)
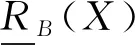
(3)
(4)
定义1.3[14]14(相对正域) 给定决策信息系统DIS=(U,C∪D,V,f),属性子集B⊆C,决策属性D在U上的决策类为U/D={D1,D2,…,Dr},则D的B正域定义为
(5)

定义1.4[14]17(依赖度) 给定决策信息系统DIS=(U,C∪D,V,f),决策属性D对条件属性集C的依赖度定义为
(6)
其含义是D的相对于C的正域对象数占全体对象集中的百分比,0≤γC(D)≤1.当γC(D)=1时代表D完全依赖于C,可以由C的知识决定D的知识(由C的分类可以确定D的分类);当γC(D)=0时代表D完全与C无关;当0<γC(D)<1时代表D部分依赖于C.特别,决策属性D相对于单个条件属性α的依赖度为
(7)
2 依赖度计算
基于粗糙集属性重要度的特征选择因其方法直观、有效而受到学者们重视,有许多学者采用了决策类对条件属性子集(特征子集)的相对依赖度来进行属性选择,属性(特征)重要度被定义为相对依赖度之差.此时,如何快速有效地计算依赖度就是一个十分重要而基础的工作.
通常计算依赖度的算法如下.

计算时间主要消耗在Step 1到Step 4,既要计算条件类与决策类,还要计算每个决策类的条件属性下近似,通常的算法时间复杂度为O(|U|2×|C|2).为了降低时间复杂度,提高运行速度,不少学者尝试改进算法.新的一个算法是章夏杰等[13]518提出的FDC算法.
输入:决策信息表.
输出:决策属性对条件属性的依赖度.
步骤1:对决策表进行预处理,将决策类属性转换成整型,并赋予每个对象唯一编号,额外添加一个标记,默认值为0.
步骤2:让每个对象xi(即编号为i的对象)与表中其余对象xj作比较,若xi的决策属性大于xj,则比较xi与xj的条件属性.若条件属性完全相同,将xi与xj的标记改为1;若存在不同属性值,则直接进入下一轮比较.
步骤3:遍历决策表,统计标记为0的对象即可求出属于正的对象数,进而求得依赖度.
FDC算法通过直接寻找基于相对正域的对象来计算依赖度,而不需要预先求出相对正域,是一个较好的思路,章夏杰等表示此算法的时间复杂度为O(|U|2×|C|/2)[13]520,复杂度降低了.
3 纵横依赖计算
在上述算法中,思路是将不属于相对正域的对象标记为1,但存在不少重复进行比较的地方,首先是每一个对象都要重复地与其他对象就决策类大小进行遍历性比较,其次是极有可能出现一个已经确定是不属于相对正域的对象就决策类与条件属性都被重复比较了多次,浪费了时间.本研究在此基础上,进一步提出一个改进算法.
改进的策略如下:
1)按决策类对元素进行排序后,不必就每一对象重复地进行决策类大小比较;
2)如果一个对象已经确认不属于相对正域,那么其他与其具有相同条件属性的同类决策类中的元素也不属于相对正域(横向比较);
3)如果一个对象已经确认不属于相对正域,就不必再将其与低阶决策类中其他对象比较(纵向比较).
实现这个策略的算法如下,这个算法不妨暂称为纵横比较依赖度算法,简称纵横依赖计算VHDC(Vertical and horizontal dependency calculation).在下面给出的VHDC算法中,为了便于编程,不仅给出框架,而且已经给出较为详细算法结构.
输入:决策信息表.
输出:决策属性对条件属性的依赖度.
第一步(预处理):将决策表按照整型决策类顺序从小到大排列,每个对象赋予唯一的ID号,同时增加一个标志列,初始值为0;记全体对象记录数为M,增加一个内存变量N,记录非正域对象数,初始值为0;设决策类共有K类,内存变量k记录第k决策类,初始值k=2,并记第k决策类有nk个对象.
第二步:如果k>K,转第四步.否则,对按决策类顺序排好的决策表中的第k类中的对象,与类别小于k的决策类中的对象进行比较操作(纵向比较),找出不属于相对正域的对象,先令l=1(l变量用于决策类层数的循环).
第三步:如果k-l<1,转第二步.否则,对第k决策类中每一个标志为0的对象xi,做如下操作:对k-l决策类中的对象的xj,比较它们的每一个条件属性值,直到比较完k-l决策类中的所有对象;
如果所有条件属性值相同,则可按如下操作进行.
1)如果xj的标志为1,则将xi的标志改为1,N=N+1,停止将第k决策类的对象xj继续与其他低层决策类的对象比较(停止该对象的纵向比较);同时将第k决策类中其余标志为0的对象与xi比较,如果所有条件属性相同,则将标志改为1,N=N+1,直到这一决策类比较完毕(横向比较);然后令l=1,转第三步,对下一个第k决策类中标志为0的对象xi进行比较;如果第k类中的对象已经比较完毕,则k=k+1,转第二步进行高1阶决策类的比较.
2)如果xj的标志为0,则有将xi,xj的标志赋值为1,同时N=N+2;对第k-1决策类的其他标志为0的对象,与xi相比,如果所有条件属性相同,则将标志改为1,N=N+1;对第k决策类的其他标志为0的对象,与xi相比,如果所有条件属性相同,则将标志改为1,N=N+1,l=l+1;转第三步.
如果存在条件属性值不相同,则比较下一个k-1决策类的xj,转第三步.
第四步:输出依赖度γ=(M-N)/M.
算法分析:第一步,需要对全体对象按决策类大小进行排序,通常的排序算法其时间复杂度为O(|U|×ln|U|).排序尽管也花了一定的时间,但为后面的计算节省了大量重复计算的时间.第二、三步,采用按排序后决策类的对象来进行比较,本算法能够避免了很多重复的计算,首先是省去了对每个对象,都要遍历对象集去进行决策类的比较;其次如果第k决策类某个对象与第k-1决策类的某个标志为1的对象在各个条件属性下属性值相同,那么第k决策类这个对象就不必继续与其他更低决策类的对象进行比较了;此外,算法中还设计了同层决策类有相同条件属性值时,不必再与其他对象比较的环节,这也避免了很多重复计算.最坏情况下,是第k决策类的所有对象xi与第k-1、k-2、……、2类的所有对象xj都需要进行条件属性值的比较(一般不会出现),最好的情况是第k决策类的所有对象xi只须与第k-1决策类的对象进行条件属性比较.因此尽管此时最坏情况下的时间复杂度[为O(|U|2×|C|/2)]与FDC算法相同,但因减少了第四步的遍历、整体比较中减少大量重复的比较,故整体上比FDC算法提高了运算效率.
4 算例
下面以一个算例来说明具体的算法过程与优劣比较.数据表(见表1)中a、b、c为条件属性,D为决策属性,决策类共有4个.

表1 有4个决策类的一种快速纵横依赖计算原始表
如表2所示,根据FDC的算法,对原始表进行预处理,决策类改为整型1,2,3,4,并增加一个标志列,初始标志值全为0.而根据本研究提出的VHDC算法,预处理后按决策类顺序排列对象,如表3所示,其中对象编号为方便计算,仍按大小顺序编号.

表2 FDC算法中预处理后的结果
为方便比较,现以表3的数据形式,分别按FDC和VHDC算法分析其具体的计算过程.
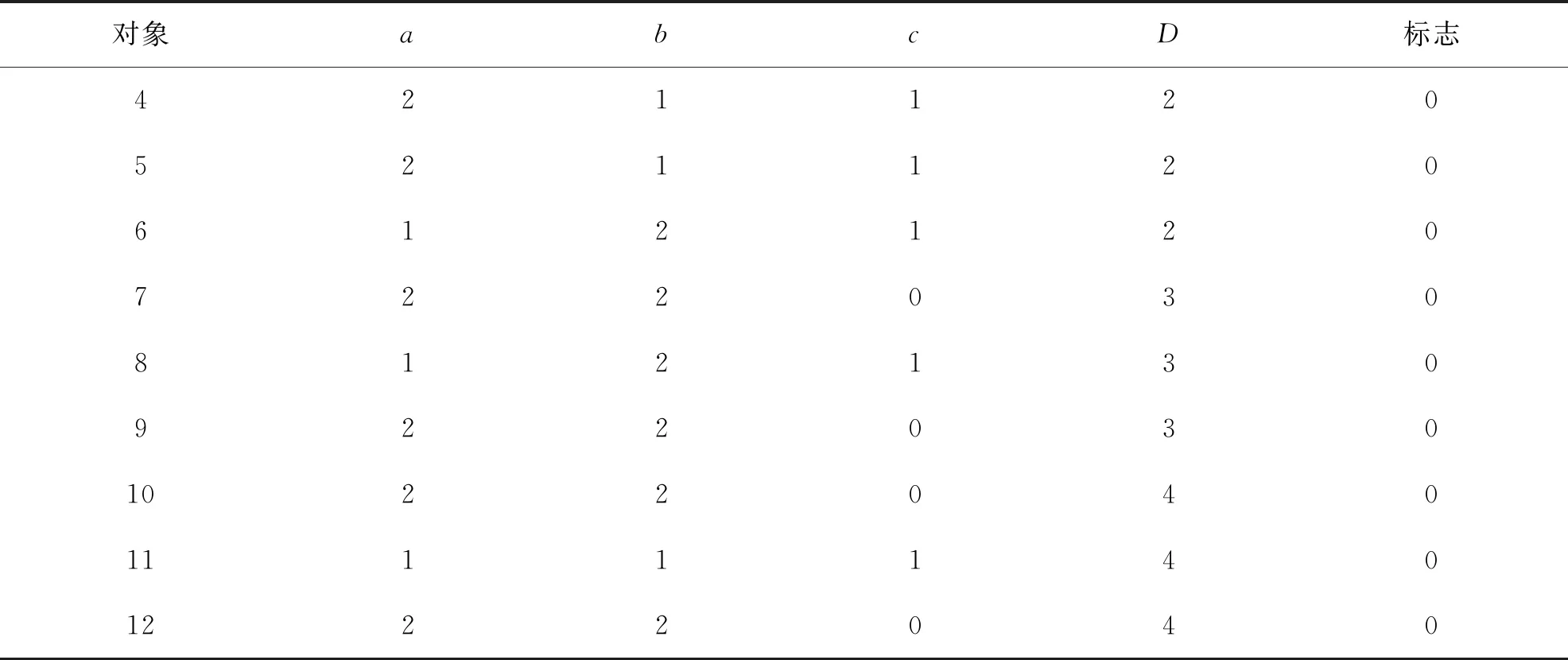
表3 VHDC算法预处理后的结果
1)FDC算法.
其算法的第二步,对所有决策类大于1的对象,都需要与比其决策类小的所有对象,进行条件属性的比较.
第1、2、3个对象:因决策类为1,没有比1更低的决策类,故不需要遍历对象集.其标志仍为0.
第4、5个对象:需要遍历对象集一遍,次数为(M-1),此例为11,以比较每个对象的决策类是否小于2,是则进行条件属性值比较,否则不进行.该对象决策类别为2,还需要对决策类别为1的3个对象,对所有条件属性分别进行比较,因不全相同,所以标志仍为0.决策类大小的比较共有(M-1)次;条件属性值的比较共有3*n1次.
第6个对象:需要遍历对象集一遍,次数为(M-1),此例为11,该对象决策类别为2,还需要对决策类别为1的3个对象,进行条件属性值比较,发现与第1决策类第2个对象的条件属性全相同,所以将这两个对象的标志均改为1.决策类大小的比较共(M-1)次;条件属性值的比较共3*n1次;改标志值共2次.
第7个对象:需要遍历对象集一遍,次数为(M-1),此例为11,该对象决策类别为3,还需要对决策类别为1的3个对象,及决策类别为2的3个对象,进行条件属性值比较.没有条件属性全相同的对象,所以标志仍为0.决策类大小的比较共(M-1)次;条件属性值的比较共(3*n1+3*n2)次.
第8个对象:需要遍历对象集一遍,次数为(M-1),此例为11.该对象决策类别为3,还需要对决策类别为1的3个对象,及决策类别为2的3个对象,进行条件属性值比较.首先发现与第1决策类的第2个对象所有条件属性值相同,所以先将这两个对象的标志改为1;然后又发现与第2决策类第6个对象的条件属性值全相同,所以又将这两个对象的标志均改为1.本来第8个对象的标志已经是1了,还要再改为1,说明有些重复.决策类大小的比较共(M-1)次;条件属性值的比较共(3*n1+3*n2)次;改标志共4次.
第9个对象:需要遍历对象集一遍,次数为(M-1),此例为11.该对象决策类别为3,还需要对决策类别为1的3个对象,及决策类别为2的3个对象,进行条件属性值比较.没有条件属性全相同的对象,所以标志仍为0.决策类大小的比较共(M-1)次,条件属性值的比较共(3*n1+3*n2)次.
第10个对象:需要遍历对象集一遍,次数为(M-1),此例为11,该对象决策类别为4,还需要对决策类别为1、2、3的共9个对象,进行条件属性值比较.首先发现与第3决策类的第7个对象所有条件属性值相同,所以先将这两个对象的标志改为1;然后又发现与第3决策类第9个对象的条件属性值全相同,所以又将这两个对象的标志均改为1.本来第10个对象的标志已经是1了,还要再改为1,说明有些重复.决策类大小的比较共(M-1)次;条件属性值的比较共(3*n1+3*n2+3*n3)次;改标志共4次.
第11个对象:需要遍历对象集一遍,次数为(M-1),此例为11.该对象决策类别为4,还需要对决策类别为1、2、3的共9个对象,进行条件属性值比较.结果没有发现与其条件属性值全相同者,决策类大小的比较共(M-1)次;条件属性值的比较共(3*n1+3*n2+3*n3)次.
第12个对象:需要遍历对象集一遍,次数为(M-1),此例为11.该对象决策类别为4,还需要对决策类别为1、2、3的共9个对象,进行条件属性值比较.首先发现与第3决策类的第7个对象所有条件属性值相同,所以先将这两个对象的标志改为1;然后又发现与第3决策类第9个对象的条件属性值全相同,所以又将这两个对象的标志均改为1.本来第7、9个对象的标志已经是1了,还要再改为1,说明有些重复.决策类大小的比较共(M-1)次;条件属性值的比较共(3*n2+3*n2+3*n3)次;改标志共4次.
FDC算法总体的算法是,对任一固定对象,先遍历所有对象与其比较,判断其他对象的决策类是否比其小,若否,则转下一个对象;若是,则还需要比较它们在每一个条件属性上的取值是否相同,如果相同,则无论原来被比较的对象标志是否为1,都要重新将其置为1.这样,在本例中,其第二步总的比较次数是
|U|*(|U|-1)+n2*n1*|C|+n3*(n2+n1)*|C|+n4*(n3+n2+n1)*|C|=294,
(8)
同时标志被改动次数为9次(实际非正域个数为7).
2)VHDC算法
由上可见,FDC算法中存在大量重复计算的现象,影响了其效率.作为对照,现在来看看由本研究提出的改进算法VHDC算法,此时的计算进程:
第1、2、3个对象:因决策类为1,没有比1更低的决策类,故不需要遍历对象集.其标志仍为1.这一步与FDC算法一样.
第4、5个对象:该对象决策类别为2,不需要遍历论域,只需要对决策类别为1的3个对象,进行条件属性值比较,因不全相同,所以标志仍为0.比较条件属性值共3*n1次,因已经对决策类排好序了,此时不需要比较决策类,下同.FDC需要遍历对象集一遍,才能判断对象是否属于第几类.
第6个对象:该对象决策类别为2,不需要遍历论域,只需要对决策类别为1的3个对象,进行条件属性值比较,发现与第1决策类第2个对象的条件属性全相同,所以将这两个对象的标志均改为1.同时,非相对正域对象数N=0+2=2.同时在第1类对象中继续遍历检查是否还有与该对象条件属性全相同者,在第2决策类对象中往后继续遍历检查是否还有与该对象条件属性全同者,当前情形没有.比较条件属性值共小于[3*n1+3*(n2-1)]次.FDC需要遍历对象集一遍,VHDC仅需要依次遍历第2、1决策类的对象.
第7个对象:该对象决策类别为3,先按顺序对决策类别为2的3个对象进行比较,发现没有与其条件属性值全同者,故再与第1决策类的对象进行比较,仍没有条件属性全相同的对象,所以标志仍为0.比较条件属性值,比较次数为(3*n1+3*n2).FDC需要遍历对象集一遍,VHDC仅需要依次遍历第2、1决策类的对象.
第8个对象:该对象决策类别为3,先按顺序对第2决策类的3个对象进行比较,发现第2决策类最后一个对象即第6个对象与其条件属性值全同者,而第6个对象的标志已经为1,故只须将这第8个对象的标志改为1,同时,非相对正域对象数N=N+1=2+1=3;然后再横向比较:第2决策类已经到最后一个,不用再继续,第3决策类再与第9个对象比较,没有条件属性全相同的对象,所以标志不改.此时,不再与第1决策类比较.比较条件属性值,共比较次数为(3*n2+1).FDC需要遍历对象集一遍,且重复更改了第2个对象的标志;VHDC仅需要依序遍历第3、2决策类的对象,且统计了到目前为止的非相对正域对象数N.
第9个对象:该对象决策类别为3,先按顺序对决策类别为2的3个对象进行比较,发现没有与其条件属性值全同者,故再与第1决策类的对象进行比较,仍没有条件属性全相同的对象,所以标志仍为0.比较条件属性值次数为(3*n1+3*n2).FDC需要遍历对象集一遍,VHDC仅需要依序遍历第2、1决策类的对象.
第10个对象:该对象决策类别为4,先按顺序对第3决策类的对象进行比较,发现第3决策类最后一个对象即第9个对象与其条件属性值全同者,故将这两个对象的标志改为1,同时,非相对正域对象数N=N+2=3+2=5;然后再横向比较:第3决策类第7个对象也与其条件属性值全同,将第7个对象标志改为1,N=N+1=5+1=6;第4决策类第12个对象也与其条件属性值全同,故将第12个对象标志改为1,N=N+1=6+1=7.此时,不再与第2、1决策类比较.比较条件属性次数为(3*n3+3*n4).FDC需要遍历对象集一遍,且重复更改了上述几个对象的标志;VHDC仅需要依序遍历第4、3决策类的对象,且统计了到目前为止的非相对正域对象数N.
第11个对象:决策类别为4,先与第3决策类对象进行比较,无条件属性值全同,再与第2决策类对象进行比较,同样无条件属性值全同,故再与第1决策类对象比较,仍无全同者,比较完毕,标志仍为0(没有改动).比较条件属性次数为[3*n3+3*(n2+n1)].这种情形比较条件属性次数与FDC算法一样,但不必进行决策类别的遍历性比较.
第12个对象:因其标志已经为1,不必再进行任何比较.而FDC仍需要遍历对象集一遍.
通过比较,可以发现VHDC算法比FDC算法减少了很多不必要的重复比较.此例中,关键一步VHDC比较的次数只有163,远小于FDC的294次.
执行VHDC算法第二、三步后的结果与执行FDC算法第二步后的结果相同,参见表4.
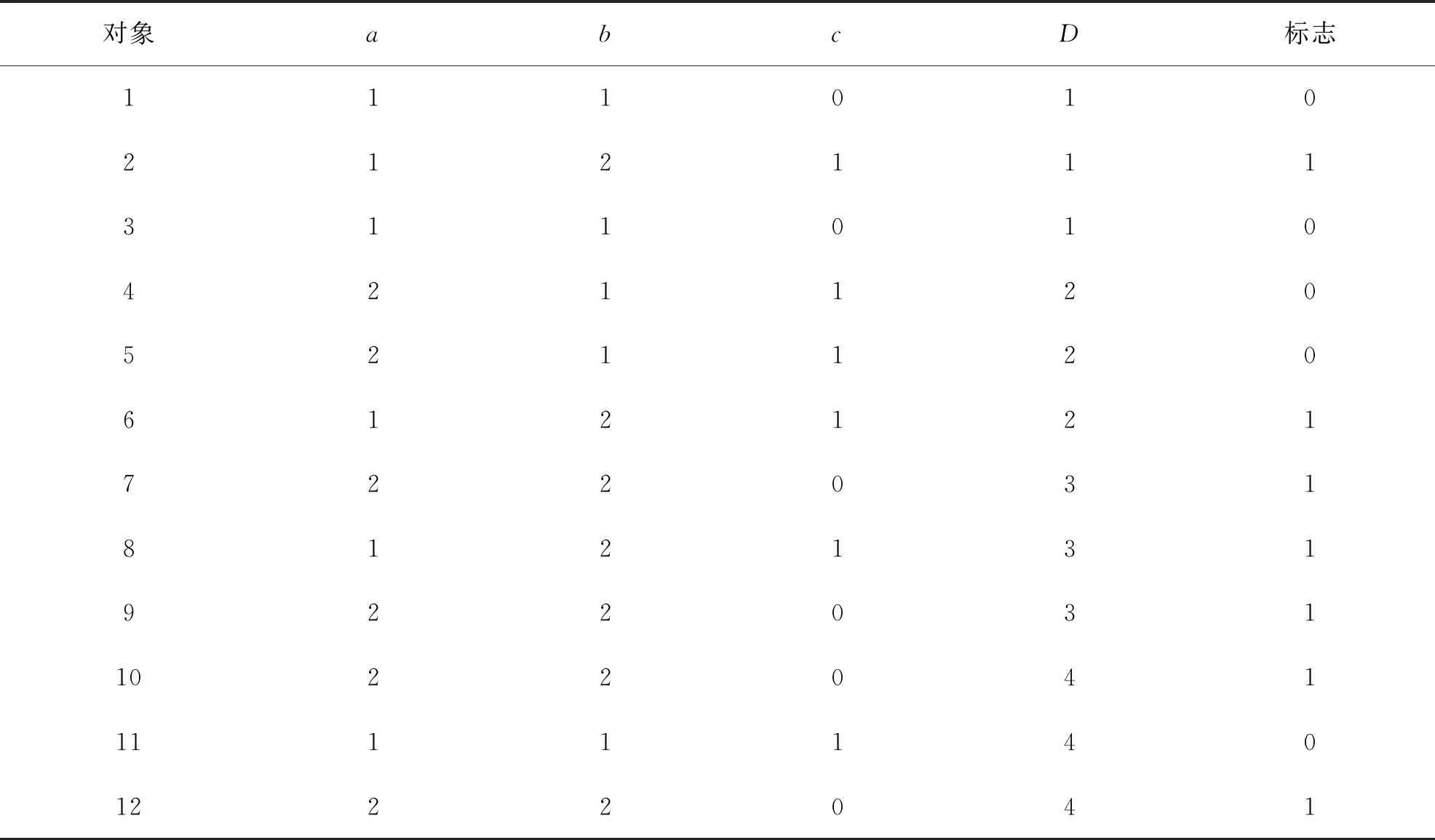
表4 执行VHDC算法与FDC算法后的结果
此例中,加上预处理与计算依赖度均需要遍历对象集,FDC最终计算次数是12+294+12=318次.而VHDC预处理计算次数为12*log212=43,计算依赖度不需要额外的遍历,其最终计算次数是43+163=206次,效率提高了35%.当数据规模很大时,其优势将更显突出.
5 结论
依赖度的计算在特征选择、属性约简等方面有重要的应用,研究快速依赖度算法具有十分重要的实际意义.本研究提出的纵横依赖计算算法,进一步降低了时间复杂性,提高了运算效率,为特征选择及属性约简提供了一种新的快速计算途径.实例表明,其效率是高的、可行的.下一步将结合属性重要性及单属性依赖度研究更高效的算法.
