基于DE-CSO混合算法的多目标无功优化
2020-11-06卢维佳黄海涛魏明磊
卢维佳,黄海涛,魏明磊
(1.广东电网汕尾供电局,广东 汕尾 516600; 2.国网安徽省电力有限公司定远供电局,安徽 滁州 233200)
0 引 言
多目标无功潮流优化是一个多变量、多约束混合的非线性规划问题[1],它通过调整系统中发电机端电压、变压器分接头及无功补偿设备的投切来改变无功潮流,从而降低系统的有功损耗、提高电压稳定裕度,同时使系统的节点电压保持在额定范围内。常规的无功优化求解智能方法已经有很多,包括粒子群算法[2-4]、差分进化算法[5]、遗传算法[6-8]等。但这些算法自身在优化过程容易导致粒子早熟,陷入局部最优。另外,单一的智能优化算法不能够提高粒子的多样性,优化后的多目标函数可行解分布不够均匀、广泛,限制了不同需求者对多目标无功优化可行解的选择。
本文提出一种融合CSO算法[9-11]和DE算法的DE-CSO算法。CSO算法参数少,调整策略相对单一,但该算法通过纵横两部分交叉操作产生的新种群不容易陷入早熟收敛。DE算法收敛速度快,种群粒子多样性好,但是该算法容易导致早熟收敛,收敛精度不够。而将两种算法相结合的DE-CSO算法不仅保留了CSO算法种群粒子不易陷入早熟收敛的特点,而且通过DE-CSO算法中的变异交叉操作,能够有效地提高粒子多样性,对于无功优化这样的非线性问题求解有很好的适用性。另外,针对多目标函数优化问题,本文通过快速非支配排序和计算粒子拥挤距离的方法来实现对粒子的优胜劣汰,产生均匀、广泛的Pareto前沿分布。
1 多目标无功优化的数学模型
1.1 多目标函数
多目标无功优化数学模型是在满足系统和发电机组运行约束的前提下,通过改变发电机端电压、变压器分接头及无功补偿设备的投切,使系统的有功网损及电压偏移最小,电压稳定裕度最大。
1)系统网损最小
式中:Ploss为系统的有功网损;NE为系统总支路数;Gk(i、j)为支路k电导;Vi、Vj、δij分别为支路k两端节点i、j的电压幅值及其相角差。
2)电压偏差量最小
式中:NPQ为系统负荷节点总数;Vspc为节点i额定电压;Vimax、Vimin分别为节点i的最大、最小允许偏差。
3)静态电压稳定裕度最大
静态电压稳定裕度是指系统当前运行点到电压崩溃点间的距离。本文采用最小特征值模[2]作为静态电压稳定裕度指标,这是因为最小特征值模能够由潮流雅可比矩阵直接求得,方便算法运行。当电力系统由正常工作点向电压崩溃点过渡时,系统雅可比矩阵最小特征值模单调地趋向于0。为了使多目标函数中每个函数都具有最小化的形式,对静态电压稳定裕度取负。因此,静态电压稳定裕度最大的目标函数为
minF3=-(min(|eig(J)|))
式中:J为收敛潮流雅可比矩阵;eig(J)为雅可比矩阵的所有特征值。
综上所述,本文建立的目标函数为
1.2 约束条件
1)等式约束条件
式中:PGi、QGi分别为节点i注入的有功功率和无功功率;Pdi、Qdi分别为节点i的负荷有功功率和无功功率;ui、uj分别为节点i、j的电压;n为系统节点总数;Qci为节点i的电容器无功补偿量;Gij、Bij分别为节点i、j之间的电导、电纳;θij为节点i、j的电压相角差。
2)不等式约束条件:
式中:Tk为变压器分接头档位。
2 DE-CSO优化算法及在多目标无功优化中的应用
2.1 CSO算法原理
假设CSO算法的种群用矩阵B表示,矩阵中的每一行用B(i)表示,代表问题的一个解,B(i,j)表示矩阵中的每一个元素,种群规模M即矩阵的行数,解空间维数D即矩阵列数。横向交叉和纵向交叉得到的解称为折中解,分别用MShc和MSvc表示。
1)横向交叉
横向交叉是在种群中两个不同个体所有维之间进行的一种算数交叉。父代个体X(i)和X(j)的第d维进行横向交叉,产生的第d维后代的折中解MShc(i,d)和MShc(j,d)采用式(1)进行计算:
(1)
其中:r1、r2∈[0,1];c1∈[-1,1];X(i,d)、X(j,d)分别是父代种群X(i)和X(j)的第d维。
随机抽取矩阵DSvc中不同行的2个粒子,抽取共进行M/2次,被选中的个体(如X(no1)和X(no2))通过式(1)产生他们的后代(MShc(no1)和MShc(no2))。
2)纵向交叉
纵向交叉是所有个体都会参与自身个体不同维之间的一种算数交叉。假定父代个体X(i)的第d1维和第d2维进行纵向交叉,产生的第d1维后代[12]MSvc(i,d1)采用式(2)进行计算:
MSvc(i,d1)=r·X(i,d1)+(1-r)·X(i,d2)
(2)
式中:d1、d2∈[1,D];i∈[1,M];r∈[0,1]。
由于纵向交叉法是对于所有种群不同维的运算操作,故先对父代种群即经横向交叉后保留下来的矩阵DShc进行归一化处理,然后随机抽取不同行的2列数据,每个列数有且只有一次被选中(如d1列和d2列),再通过式(2)产生新的子代(MSvc(i,d1)),最后对新的种群进行反归一化处理。纵向交叉抽取共进行D/2次,只改变D/2列的数据,其目的是促使可能陷入停滞不前的维(如d1)跳出局部最优,同时不破坏另外可能正常进化的维(如d2)。
2.2 DE算法原理
DE算法主要通过变异操作和交叉操作来产生新的后代。
1)变异操作
DE算法从群体中任意选取3个互不相同的染色体进行加权变异,产生子代染色体,计算式如下:
yi=xno1+F·(xno2-xno3)
(3)
式中:xno1、xno2、xno3为3个互不相同的染色体;F为缩放因子。
标准的DE算法中F为固定数值,F值对算法的全局寻优能力有很大影响。F选择过小,算法容易陷入早熟收敛;F选择过大,算法收敛速度会变慢。为了能够解决易早熟和迭代收敛速度较慢的问题,提出一种自适应缩放因子Fi,其计算式为
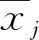
2)交叉操作
DE算法将父代粒子维度按一定概率与变异粒子维度执行交叉操作,计算式如下:
(4)
式中:CR为交叉概率;yi,j是变异操作后第i条染色体的第j个基因。
DE算法通过交叉操作保留父代粒子的特征,使算法在优化过程中能够有效地保持粒子多样性。
2.3 多目标函数的处理
由于多目标无功优化的目标函数之间存在相互矛盾性,因此很难找到一个可以使各目标函数同时达到最优的解,如何评价这些解的优劣性是该问题求解的难点之一。目前,绝大部分算法采用加权叠加比较的评价方法,但是该方法不能很好地反应各目标函数的优劣性。本文通过多目标快速非支配排序法[12-13]和比较粒子拥挤距离的方式得到所有解中的Pareto最优前沿[14],并采用模糊隶属度寻找最优解。
1)快速非支配排序法
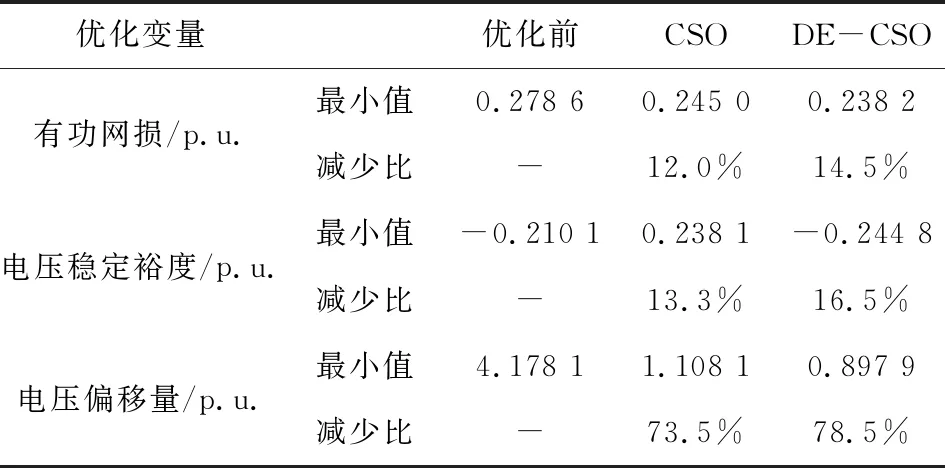
对于目标函数fi的两个可行解a和b,满足任意fi(a)≤fi(b)(i=1,2,…,n)且存在fi使得fi(a) 2)拥挤距离 (5) 式中:f[i]p为第i个种群中第p个目标函数中的解。 比较每个粒子的拥挤距离,拥挤距离越大,粒子具有越好的多样性和寻优性,经过多次迭代,能够使Pareto前沿分布更加均匀。 针对CSO算法和DE算法在优化过程中的缺点,DE-CSO优化算法混合了CSO算法中纵向交叉操作、横向交叉操作及DE算法中变异、交叉操作。在更新粒子种群时,分别对父代粒子进行变异、交叉和纵横交叉操作,然后再将产生的子代粒子与父代粒子进行比较,从而实现粒子的优胜劣汰。通过多种更新子代粒子的方式,DE-CSO算法能够融合两种算法的优点,使新种群能够跳出局部最优,提高收敛精度和粒子多样性。为了将DE-CSO算法应用到多目标函数中,混合算法不保留基本纵横交叉算法中竞争算子的运算,而是采用多目标快速非支配排序法和比较粒子拥挤距离的方式来评价子代粒子和父代粒子的优劣性。通过多次迭代后,粒子的Pareto前沿分布更加广泛、均匀。将DE-CSO算法应用在多目标无功优化问题上,其算法步骤如下所述,流程图如图1所示。 图1 多目标DE-CSO优化算法流程图 1)设置算法参数、控制变量,初始种群为F1。 2)将种群F1粒子带入式(3)、(4)进行粒子变异和交叉操作,产生子代种群,并合并父代和子代,形成种群规模为2n的混合种群F2。 4)运用快速非支配排序法和计算粒子拥挤距离的择优策略从混合种群F2中选择种群数为n的优秀粒子,形成新种群F3。 5)执行CSO算法运算。将种群F3的粒子带入式(1)、(3)进行横向交叉操作和纵向交叉操作,产生种群F6。 6)合并混合种群F3和F6,执行步骤4)产生新种群F7,并用种群F7覆盖种群F1。 7)更新Pareto前沿分布,检验是否满足迭代次数,满足则退出运行,输出结果;否则转回步骤2)。 本文使用IEEE14、IEEE57标准节点系统进行仿真实验。算法参数设置如下:种群规模为50,最大迭代次数为200,CSO算法中的横向交叉概率为1,纵向交叉概率为0.6,差分算法的交叉率为 0.5,变异率为 0.5。在测试中除平衡节点外,电源节点都作为PV节点处理,负荷节点都作为PQ节点处理。变压器变比上限为1.1,下限为0.95,变量步长为0.05;无功补偿为0.0~0.5 p.u.,调节步长为0.1 p.u.;发电机节点电压上、下极限分别为1.1、0.9,变量步长为0.05。 该系统包含20条支路,有3台变压器、5台发电机、1个无功补偿点,其中节点1为平衡节点,节点2、3、6、8为PV节点,系统数据详见文献[15]。为了更加清晰地对比不同算法的仿真效果,IEEE14节点系统只考虑有功网损和电压稳定裕度两个目标。运用CSO算法、DE-CSO算法对该系统进行无功优化,仿真效果对比如图2所示。 图2 IEEE14节点系统中两种算法的Pareto前沿分布 对比CSO算法、DE-CSO算法仿真的曲线可以看出,经过DE-CSO优化后的Pareto前沿分布更加均匀、广泛,其收敛精度更高。这是因为DE-CSO算法融合了DE算法和CSO算法各自的优点,它一方面弥补了DE算法在优化过程中容易陷入局部最优的缺点,通过CSO算法纵横交叉体制产生的新种群能够有效跳出局部最优,提高收敛精度;另一方面融合了DE算法中的交叉操作和变异操作,改变了CSO算法收敛速度慢、调整策略单一的缺点,有效地提高了种群的多样性。所以,运用DE-CSO算法优化后的多目标无功优化Pareto前沿分布明显优于传统的CSO算法,数据对比如表1所示。 表1 IEEE14节点系统结果对比 该系统包含41条支路,有15台变压器、7台发电机、3个无功补偿点,其中节点1为平衡节点,节点2、3、6、8、9、12为PV节点。分别运用CSO算法、DE-CSO算法对该系统进行无功优化,系统数据详见文献[15]。仿真效果如图3、4所示。 图3 IEEE57节点CSO算法Pareto前沿分布 对比CSO算法和DE-CSO算法优化后的三维仿真效果图可以看出,DE-CSO算法产生的Pareto前沿分布均匀、广泛,同时收敛精度更高,其优化效果明显优于传统的CSO算法,充分地显示了混合算法良好的收敛能力及寻优效率,达到了预期的效果,数据对比如表2所示。 图4 IEEE57节点 DE-CSO算法Pareto前沿分布 表2 IEEE57节点系统结果对比 为了解决电力系统无功优化多约束、多变量的问题,创新性地提出了一种融合DE算法和CSO算法的多目标DE-CSO算法。新算法改进了标准DE算法和CSO算法,提高了算法的收敛效率,能有效地防止粒子陷入局部最优。同时,在采用非支配排序法的基础上,通过DE-CSO算法的运算增加了粒子的多样性。为提高Pareto分布的均匀性,通过计算粒子间的拥挤距离来控制目标函数的解集。在IEEE14和IEEE57节点的系统中进行仿真,产生Pareto多目标分布前沿。仿真结果表明,新算法能有效地降低电力系统有功网损和电压偏移量、提高静态电压稳定裕度,为解决电力系统无功优化问题提供了新的思路。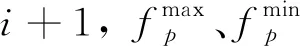
2.4 多目标DE-CSO优化算法及应用

3 算例分析
3.1 IEEE14节点算例
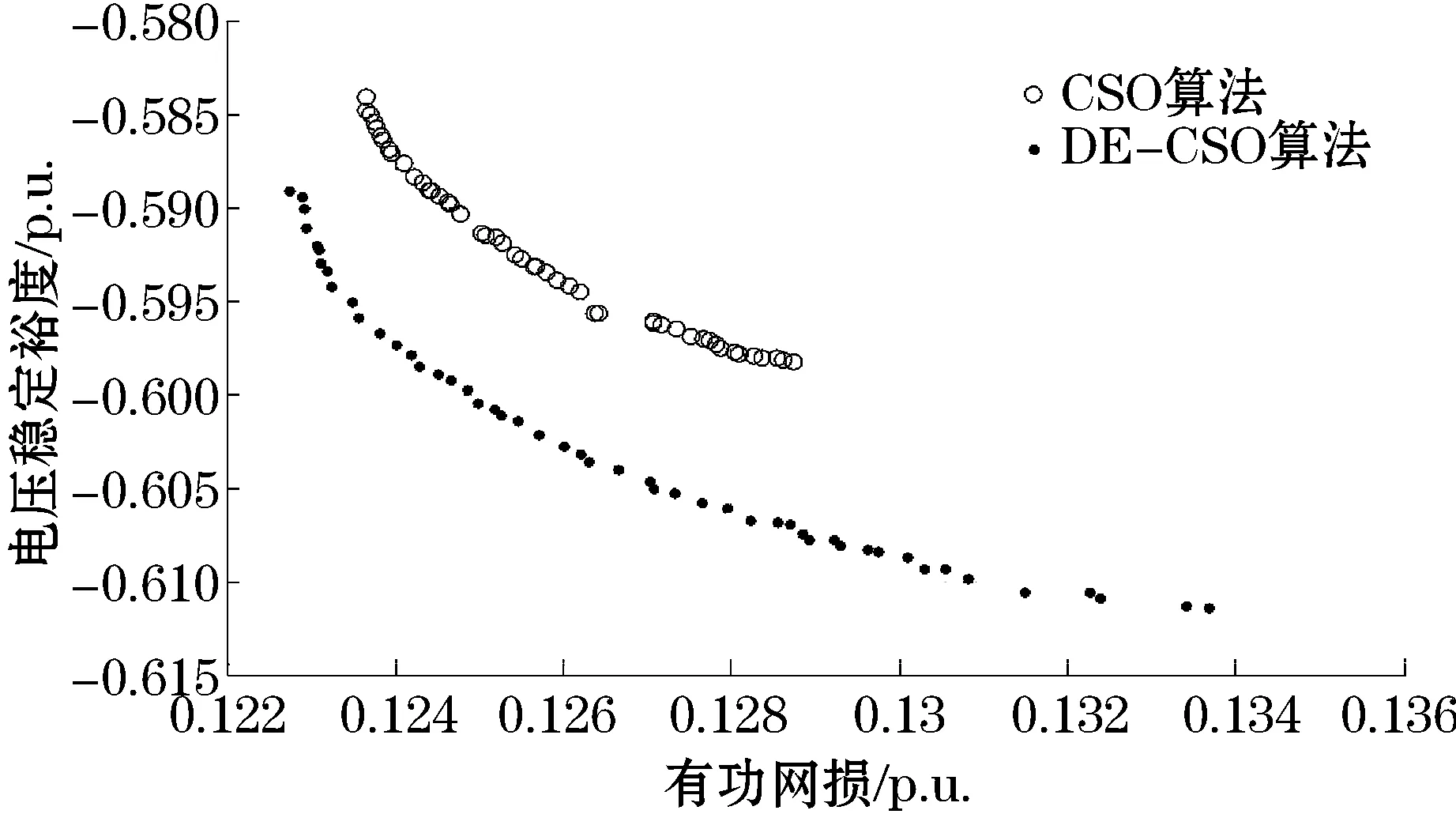

3.2 IEEE57节点算例
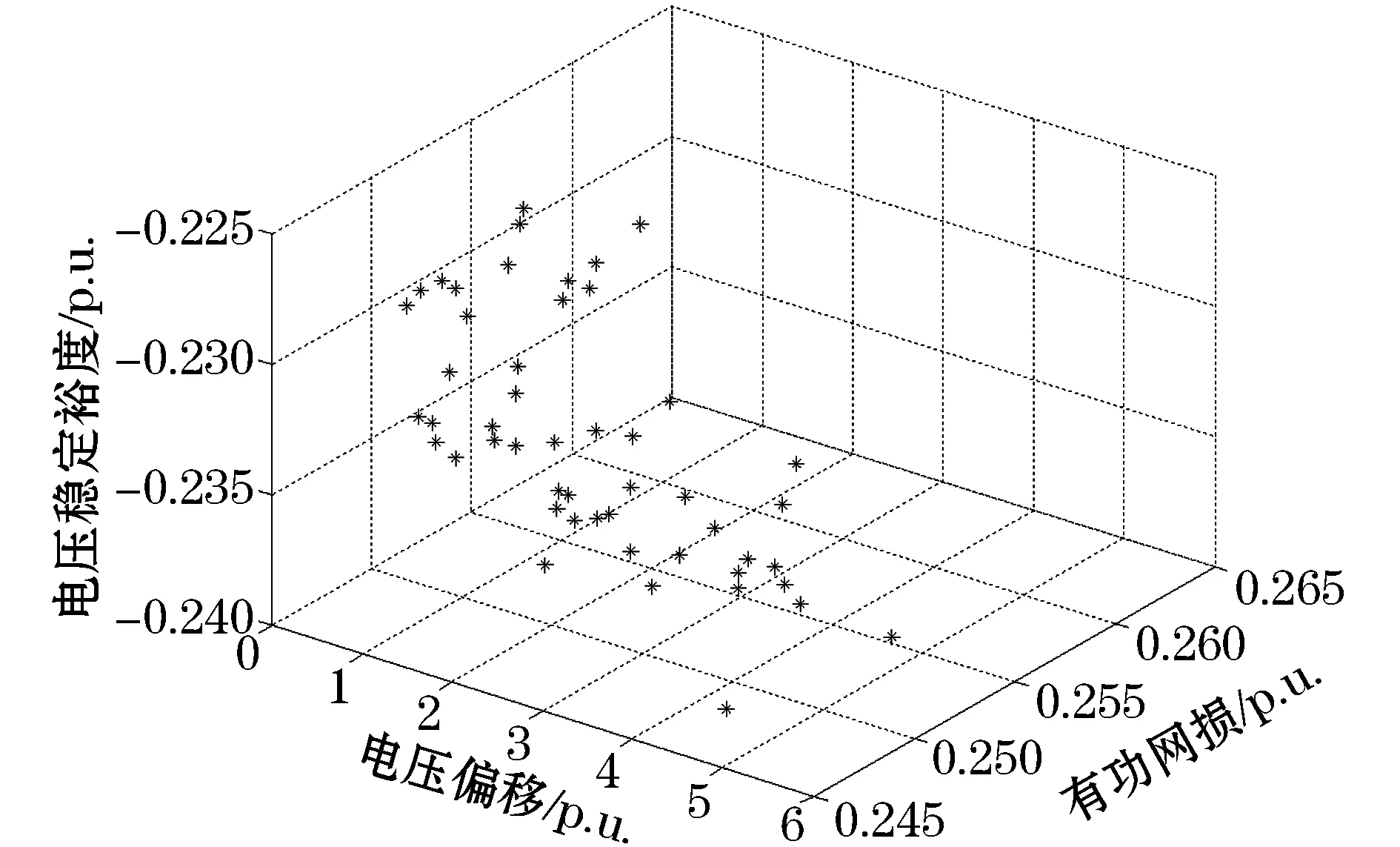

4 结 语
